【蓝桥杯算法练习题】树状数组与线段树

一、AcWing 1264. 动态求连续区间和

【题目描述】
给定$n$个数组成的一个数列，规定有两种操作，一是修改某个元素，二是求子数列$[a,b]$的连续和。

【输入格式】
第一行包含两个整数$n$和$m$，分别表示数的个数和操作次数。
第二行包含$n$个整数，表示完整数列。
接下来$m$行，每行包含三个整数$k,a,b$（$k=0$，表示求子数列$[a,b]$的和；$k=1$，表示第$a$个数加$b$）。
数列从$1$开始计数。

【输出格式】
输出若干行数字，表示$k=0$时，对应的子数列$[a,b]$的连续和。

【数据范围】
$1\le n\le 100000$
$1\le m\le 100000$
$1\le a\le b\le n$
数据保证在任何时候，数列中所有元素之和均在$int$范围内。

【输入样例】

10 5
1 2 3 4 5 6 7 8 9 10
1 1 5
0 1 3
0 4 8
1 7 5
0 4 8

【输出样例】

11
30
35

【分析】

---

树状数组模板题~

---

【树状数组代码】

#include 
#include 
#include 
using namespace std;

const int N = 100010;
int c[N];
int n, m;

int lowbit(int x)
{
    return x & -x;
}

void add(int x, int y)
{
    for (; x <= n; x += lowbit(x)) c[x] += y;
}

int ask(int x)
{
    int res = 0;
    for (; x; x -= lowbit(x)) res += c[x];
    return res;
}

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) { int x; cin >> x; add(i, x); }
    while (m--)
    {
        int k, a, b;
        cin >> k >> a >> b;
        if (!k) cout << ask(b) - ask(a - 1) << endl;
        else add(a, b);
    }
    return 0;
}

【线段树代码】

#include 
#include 
#include 
using namespace std;

const int N = 100010;
int w[N];
int n, m;

struct Node
{
    int l, r, sum;
}tr[N << 2];

void pushup(int u)
{
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}

void build(int u, int l, int r)
{
    if (l == r) tr[u] = { l, r, w[r] };
    else
    {
        tr[u] = { l, r };
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }
}

void modify(int u, int x, int y)
{
    if (tr[u].l == x && tr[u].r == x) tr[u].sum += y;
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid) modify(u << 1, x, y);
        else modify(u << 1 | 1, x, y);
        pushup(u);
    }
}

int query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        int res = 0;
        if (l <= mid) res += query(u << 1, l, r);
        if (r > mid) res += query(u << 1 | 1, l, r);
        return res;
    }
}

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> w[i];
    build(1, 1, n);
    while (m--)
    {
        int k, a, b;
        cin >> k >> a >> b;
        if (!k) cout << query(1, a, b) << endl;
        else modify(1, a, b);
    }
    return 0;
}

二、AcWing 1265. 数星星

【题目描述】
天空中有一些星星，这些星星都在不同的位置，每个星星有个坐标。
如果一个星星的左下方（包含正左和正下）有$k$颗星星，就说这颗星星是$k$级的。

例如，上图中星星$5$是$3$级的（$1,2,4$在它左下），星星$2,4$是$1$级的。
例图中有$1$个$0$级，$2$个$1$级，$1$个$2$级，$1$个$3$级的星星。
给定星星的位置，输出各级星星的数目。
换句话说，给定$N$个点，定义每个点的等级是在该点左下方（含正左、正下）的点的数目，试统计每个等级有多少个点。

【输入格式】
第一行一个整数$N$，表示星星的数目；
接下来$N$行给出每颗星星的坐标，坐标用两个整数$x,y$表示；
不会有星星重叠。星星按$y$坐标增序给出，$y$坐标相同的按$x$坐标增序给出。

【输出格式】
$N$行，每行一个整数，分别是$0$级，$1$级，$2$级，…，$N-1$级的星星的数目。

【数据范围】
$1\le N\le 15000$
$0\le x,y\le 32000$

【输入样例】

5
1 1
5 1
7 1
3 3
5 5

【输出样例】

1
2
1
1
0

【分析】

---

此题考查树状数组的应用，题目要求求某一个点$(x,y)$左下方星星的个数（不包括自己），且星星按$y$坐标增序给出，$y$坐标相同的按$x$坐标增序给出，因此对于每个新来的点$(x,y)$，$y$一定是当前纵坐标的最大值，且后面出现的星星要么横坐标更大要么纵坐标更大不可能会在当前星星的左下角，因此我们只需要求在当前星星之前出现的横坐标在$[1,x]$中的星星出现的数量即可。然后再将当前星星所在的横坐标$x$出现的星星数量加一即可。该操作可以使用树状数组完成。
注意：树状数组下标是从$1$开始的，而题目的给定的$x$范围是$0\le x\le 32000$，因此需要将所有的$x$转变成$x+1$（相对位置不变）。

---

【代码】

#include 
#include 
#include 
using namespace std;

const int N = 32010;
int c[N], cnt[N];
int n;

int lowbit(int x)
{
    return x & -x;
}

void add(int x)
{
    for (; x < N; x += lowbit(x)) c[x]++;
}

int ask(int x)
{
    int res = 0;
    for (; x; x -= lowbit(x)) res += c[x];
    return res;
}

int main()
{
    cin >> n;
    for (int i = 0; i < n; i++)
    {
        int x, y;
        cin >> x >> y;
        x++;//由于树状数组下标从1开始因此要将所有横坐标加一
        cnt[ask(x)]++;
        add(x);
    }
    for (int i = 0; i < n; i++) cout << cnt[i] << endl;
    return 0;
}

三、AcWing 1270. 数列区间最大值

【题目描述】
输入一串数字，给你$M$个询问，每次询问就给你两个数字$X,Y$，要求你说出$X$到$Y$这段区间内的最大数。

【输入格式】
第一行两个整数$N,M$表示数字的个数和要询问的次数；
接下来一行为$N$个数；
接下来$M$行，每行都有两个整数$X,Y$。

【输出格式】
输出共$M$行，每行输出一个数。

【数据范围】
$1\le N\le 10^5$
$1\le M\le 10^6$
$1\le X\le Y\le N$
数列中的数字均不超过$2^{31}-1$

【输入样例】

10 2
3 2 4 5 6 8 1 2 9 7
1 4
3 8

【输出样例】

5
8

【分析】

---

线段树模板题~本题的输入数据量特别大，强烈建议使用scanf进行读入。注意元素可能有负数，因此初始化时查询结果应该为INT_MIN（在头文件中）。

---

【代码】

#include 
#include 
#include 
#include 
using namespace std;

const int N = 100010;
int w[N];
int n, m;

struct Node
{
    int l, r, v;
}tr[N << 2];

void pushup(int u)
{
    tr[u].v = max(tr[u << 1].v, tr[u << 1 | 1].v);
}

void build(int u, int l, int r)
{
    if (l == r) tr[u] = { l, r, w[r] };
    else
    {
        tr[u] = { l, r };
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }
}

int query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].v;
    else
    {
        int mid = tr[u].l + tr[u].r >> 1, v = INT_MIN;
        if (l <= mid) v = query(u << 1, l, r);
        if (r > mid) v = max(v, query(u << 1 | 1, l, r));
        return v;
    }
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) scanf("%d", &w[i]);
    build(1, 1, n);
    while (m--)
    {
        int l, r;
        scanf("%d%d", &l, &r);
        printf("%d\n", query(1, l, r));
    }
    return 0;
}

四、AcWing 1215. 小朋友排队

【题目描述】
$n$个小朋友站成一排。
现在要把他们按身高从低到高的顺序排列，但是每次只能交换位置相邻的两个小朋友。
每个小朋友都有一个不高兴的程度。
开始的时候，所有小朋友的不高兴程度都是$0$。
如果某个小朋友第一次被要求交换，则他的不高兴程度增加$1$，如果第二次要求他交换，则他的不高兴程度增加$2$（即不高兴程度为$3$），依次类推。当要求某个小朋友第$k$次交换时，他的不高兴程度增加$k$。
请问，要让所有小朋友按从低到高排队，他们的不高兴程度之和最小是多少。
如果有两个小朋友身高一样，则他们谁站在谁前面是没有关系的。

【输入格式】
输入的第一行包含一个整数$n$，表示小朋友的个数。
第二行包含$n$个整数$H_1,H_2,\dots ,H_n$，分别表示每个小朋友的身高。

【输出格式】
输出一行，包含一个整数，表示小朋友的不高兴程度和的最小值。

【数据范围】
$1\le n\le 100000$
$0\le H_i\le 1000000$

【输入样例】

3
3 2 1

【输出样例】

9

【样例解释】
首先交换身高为$3$和$2$的小朋友，再交换身高为$3$和$1$的小朋友，再交换身高为$2$和$1$的小朋友，每个小朋友的不高兴程度都是$3$，总和为$9$。

【分析】

---

首先根据题意可知这是一个冒泡排序的过程，假设小朋友的身高序列中存在$k$对逆序对，那么至少需要进行$k$次交换才能消去所有逆序对，因为每次交换最多只能消去一个逆序对，其它逆序对不受影响。而冒泡排序每次交换的条件是$h_i>h_{i+1}$，因此要将序列排好序就需要$k$次的交换。

那么我们再来看第$i$个小朋友，他的身高是$h_i$，在他前面的比他高的小朋友一定至少需要和他交换一次，在他后面的比他矮的小朋友也一定至少需要和他交换一次，那么我们记他前面比他高的小朋友数量为$k1$，他后面比他矮的小朋友数量为$k2$，则第$i$个小朋友就需要进行$k1+k2$次交换，我们再记$sum=k1+k2$，则第$i$个小朋友的不高兴值就是$1+2+\cdots +sum$，根据高斯求和公式可快速算出结果：$(1+sum)\ast sum/2$。

求某个数前面比它大或小的数有几个可以使用树状数组，数组记录每个数出现的次数，假设$N$是所有数中的最大值，则在$x$之前出现的比$x$大的数的数量为$c[N]-c[x]$，比$x$小的数的数量为$c[x-1]$。注意本题的$h_i$可能为$0$，树状数组下标需要从$1$开始，因此需要先将所有$h_i$加一。

---

【代码】

#include 
#include 
#include 
using namespace std;

typedef long long LL;
const int N = 100010, M = 1000010;
int c[M], h[N], sum[N];
int n;

int lowbit(int x)
{
    return x & -x;
}

void add(int x, int y)
{
    for (; x < M; x += lowbit(x)) c[x] += y;
}

int ask(int x)
{
    int res = 0;
    for (; x; x -= lowbit(x)) res += c[x];
    return res;
}

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++) { cin >> h[i]; h[i]++; }
    for (int i = 1; i <= n; i++)//正向求出每个数左边比它大的数的数量
    {
        sum[i] += ask(M - 1) - ask(h[i]);
        add(h[i], 1);//将当前数加入到树状数组中,即出现次数加一
    }
    memset(c, 0, sizeof c);
    for (int i = n; i; i--)//反向求出每个数右边比它小的数的数量
    {
        sum[i] += ask(h[i] - 1);
        add(h[i], 1);
    }
    LL res = 0;
    for (int i = 1; i <= n; i++) res += (LL)(1 + sum[i]) * sum[i] / 2;
    cout << res << endl;
    return 0;
}

五、AcWing 1228. 油漆面积

【题目描述】
X星球的一批考古机器人正在一片废墟上考古。
该区域的地面坚硬如石、平整如镜。
管理人员为方便，建立了标准的直角坐标系。
每个机器人都各有特长、身怀绝技。
它们感兴趣的内容也不相同。
经过各种测量，每个机器人都会报告一个或多个矩形区域，作为优先考古的区域。
矩形的表示格式为$(x_1,y_1,x_2,y_2)$，代表矩形的两个对角点坐标。
为了醒目，总部要求对所有机器人选中的矩形区域涂黄色油漆。
小明并不需要当油漆工，只是他需要计算一下，一共要耗费多少油漆。
其实这也不难，只要算出所有矩形覆盖的区域一共有多大面积就可以了。
注意，各个矩形间可能重叠。

【输入格式】
第一行，一个整数$n$，表示有多少个矩形。
接下来的$n$行，每行有$4$个整数$x_1,y_1,x_2,y_2$，空格分开，表示矩形的两个对角顶点坐标。

【输出格式】
一行一个整数，表示矩形覆盖的总面积。

【数据范围】
$1\le n\le 10000$
$0\le x_1,x_2,y_2,y_2\le 10000$
数据保证$x_1<x_2$且$y_1<y_2$

【输入样例1】

3
1 5 10 10
3 1 20 20
2 7 15 17

【输出样例1】

340

【输入样例2】

3
5 2 10 6
2 7 12 10
8 1 15 15

【输出样例2】

128

【分析】

---

扫描线+线段树模板题，亚特兰蒂斯的无需离散化版本。需要注意的就是我们的线段树节点维护的是一个区间，即节点$y_1$维护的是区间$[y_1,y_2-1]$。

---

【代码】

#include 
#include 
#include 
using namespace std;

const int N = 10010;
int n;

struct Segment
{
    int x, y1, y2, k;
    bool operator< (const Segment& t) const
    {
        return x < t.x;
    }
}seg[N << 1];

struct Node
{
    int l, r, cnt, len;
}tr[N << 2];

void pushup(int u)
{
    if (tr[u].cnt) tr[u].len = tr[u].r - tr[u].l + 1;
    else if (tr[u].l == tr[u].r) tr[u].len = 0;
    else tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;
}

void build(int u, int l, int r)
{
    tr[u] = { l, r, 0, 0 };
    if (l == r) return;
    int mid = l + r >> 1;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}

void modify(int u, int l, int r, int y)
{
    if (tr[u].l >= l && tr[u].r <= r)
    {
        tr[u].cnt += y;
        pushup(u);
    }
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if (l <= mid) modify(u << 1, l, r, y);
        if (r > mid) modify(u << 1 | 1, l, r, y);
        pushup(u);
    }
}

int main()
{
    cin >> n;
    int m = 0;
    while (n--)
    {
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        seg[m++] = { x1, y1, y2, 1 };
        seg[m++] = { x2, y1, y2, -1 };
    }
    sort(seg, seg + m);
    build(1, 0, 10000);
    int res = 0;
    for (int i = 0; i < m; i++)
    {
        if (i > 0) res += tr[1].len * (seg[i].x - seg[i - 1].x);
        modify(1, seg[i].y1, seg[i].y2 - 1, seg[i].k);
    }
    cout << res << endl;
    return 0;
}

六、AcWing 1232. 三体攻击（三维差分）

【题目描述】
三体人将对地球发起攻击。
为了抵御攻击，地球人派出了$A\times B\times C$艘战舰，在太空中排成一个$A$层$B$行$C$列的立方体。
其中，第$i$层第$j$行第$k$列的战舰（记为战舰$(i,j,k)$）的生命值为$d(i,j,k)$。
三体人将会对地球发起$m$轮“立方体攻击”，每次攻击会对一个小立方体中的所有战舰都造成相同的伤害。
具体地，第$t$轮攻击用$7$个参数$l{a}_t,r{a}_t,l{b}_t,r{b}_t,l{c}_t,r{c}_t,h_t$描述；
所有满足$i\in [l{a}_t,r{a}_t],j\in [l{b}_t,r{b}_t],k\in [l{c}_t,r{c}_t]$的战舰$(i,j,k)$会受到$h_t$的伤害。
如果一个战舰累计受到的总伤害超过其防御力，那么这个战舰会爆炸。
地球指挥官希望你能告诉他，第一艘爆炸的战舰是在哪一轮攻击后爆炸的。

【输入格式】
第一行包括$4$个正整数$A,B,C,m$；
第二行包含$A\times B\times C$个整数，其中第$((i-1)\times B+(j-1))\times C+(k-1)+1$个数为$d(i,j,k)$；
第$3$到第$m+2$行中，第$(t-2)$行包含$7$个正整数$l{a}_t,r{a}_t,l{b}_t,r{b}_t,l{c}_t,r{c}_t,h_t$。

【输出格式】
输出第一个爆炸的战舰是在哪一轮攻击后爆炸的。
保证一定存在这样的战舰。

【数据范围】
$1\le A\times B\times C\le 10^6$
$1\le m\le 10^6$
$0\le d(i,j,k),h_t\le 10^9$
$1\le l{a}_t\le r{a}_t\le A$
$1\le l{b}_t\le r{b}_t\le B$
$1\le l{c}_t\le r{c}_t\le C$
层、行、列的编号都从$1$开始。

【输入样例】

2 2 2 3
1 1 1 1 1 1 1 1
1 2 1 2 1 1 1
1 1 1 2 1 2 1
1 1 1 1 1 1 2

【输出样例】

2

【样例解释】
在第$2$轮攻击后，战舰$(1,1,1)$总共受到了$2$点伤害，超出其防御力导致爆炸。

【分析】

---

首先本题我们只知道体积，而不知道立方体的长宽高，因此我们只能开一维数组，那么就需要将三维坐标映射到一维上：类比于二维坐标与一维坐标的映射，三维坐标$(i,j,k)$的一维坐标为$(i\ast B+j)\ast C+k$。

假设$s$为前缀和数组，$b$为差分数组，则：

$s(x,y,z)=b(x,y,z)+s(x-1,y,z)+s(x,y-1,z)-s(x-1,y-1,z)+s(x,y,z-1)-s(x-1,y,z-1)-s(x,y-1,z-1)+s(x-1,y-1,z-1)$。

我们在将立方体的某一个子立方体（假设两个顶点分别为$(x_1,y_1,z_1)$和$(x_2,y_2,z_2)$）中的所有点减去$h$，那么需要在差分数组进行以下操作：

$b(x_1,y_1,z_1)-=h$
$b(x_1,y_1,z_2+1)+=h$
$b(x_1,y_2+1,z_1)+=h$
$b(x_1,y_2+1,z_2+1)-=h$
$b(x_2+1,y_1,z_1)+=h$
$b(x_2+1,y_1,z_2+1)-=h$
$b(x_2+1,y_2+1,z_1)-=h$
$b(x_2+1,y_2+1,z_2+1)+=h$

然后我们二分查找攻击的轮数，找出最小的使得有至少一艘战舰爆炸的攻击次数即可。

---

【代码】

#include 
#include 
#include 
using namespace std;

typedef long long LL;
const int N = 2000010;
LL s[N], b[N], backup[N];
int op[N / 2][7];//保存所有攻击
int A, B, C, m;
int d[8][4] = {
    { 0, 0, 0, 1 },
    { 0, 0, 1, -1 },
    { 0, 1, 0, -1 },
    { 0, 1, 1, 1 },
    { 1, 0, 0, -1 },
    { 1, 0, 1, 1 },
    { 1, 1, 0, 1 },
    { 1, 1, 1, -1 }
};//求差分数组时原数组下标(i,j,k)需要减去的值以及整项的符号

//将三维坐标(i,j,k)映射成一维坐标
int get(int i, int j, int k)
{
    return (i * B + j) * C + k;
}

bool check(int mid)
{
    memcpy(b, backup, sizeof backup);
    memset(s, 0, sizeof s);
    //执行前mid次攻击
    for (int i = 1; i <= mid; i++)
    {
        int x1 = op[i][0], x2 = op[i][1], y1 = op[i][2], y2 = op[i][3],
            z1 = op[i][4], z2 = op[i][5], h = op[i][6];
        b[get(x1, y1, z1)] -= h;
        b[get(x1, y1, z2 + 1)] += h;
        b[get(x1, y2 + 1, z1)] += h;
        b[get(x1, y2 + 1, z2 + 1)] -= h;
        b[get(x2 + 1, y1, z1)] += h;
        b[get(x2 + 1, y1, z2 + 1)] -= h;
        b[get(x2 + 1, y2 + 1, z1)] -= h;
        b[get(x2 + 1, y2 + 1, z2 + 1)] += h;
    }
    //求差分数组的前缀和,也就是求出原数组s(i,j,k)
    for (int i = 1; i <= A; i++)
        for (int j = 1; j <= B; j++)
            for (int k = 1; k <= C; k++)
            {
                s[get(i, j, k)] = b[get(i, j, k)];
                for (int u = 1; u < 8; u++)
                {
                    int x = i - d[u][0], y = j - d[u][1], z = k - d[u][2], t = d[u][3];
                    s[get(i, j, k)] -= s[get(x, y, z)] * t;//与求差分数组的过程相反,即符号相反
                }
                if (s[get(i, j, k)] < 0) return true;
            }
    return false;
}

int main()
{
    scanf("%d%d%d%d", &A, &B, &C, &m);
    for (int i = 1; i <= A; i++)
        for (int j = 1; j <= B; j++)
            for (int k = 1; k <= C; k++)
                scanf("%lld", &s[get(i, j, k)]);
    //读入m次攻击操作
    for (int i = 1; i <= m; i++)
        for (int j = 0; j < 7; j++)
            scanf("%d", &op[i][j]);
    //求差分数组backup(i,j,k)
    for (int i = 1; i <= A; i++)
        for (int j = 1; j <= B; j++)
            for (int k = 1; k <= C; k++)
                for (int u = 0; u < 8; u++)
                {
                    int x = i - d[u][0], y = j - d[u][1], z = k - d[u][2], t = d[u][3];
                    backup[get(i, j, k)] += s[get(x, y, z)] * t;
                }
    int l = 1, r = m;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }
    cout << r << endl;
    return 0;
}

七、AcWing 1237. 螺旋折线

【题目描述】
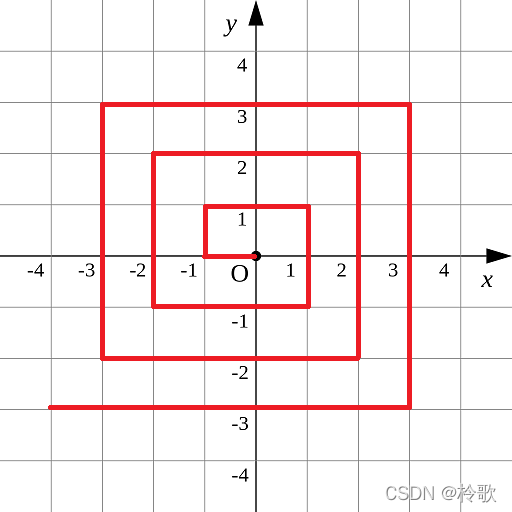
如下图所示的螺旋折线经过平面上所有整点恰好一次。

对于整点$(X,Y)$，我们定义它到原点的距离$dis(X,Y)$是从原点到$(X,Y)$的螺旋折线段的长度。
例如$dis(0,1)=3,dis(-2,-1)=9$。
给出整点坐标$(X,Y)$，你能计算出$dis(X,Y)$吗？

【输入格式】
包含两个整数$X,Y$。

【输出格式】
输出一个整数，表示$dis(X,Y)$。

【数据范围】
$-10^9\le X,Y\le 10^9$

【输入样例】

0 1

【输出样例】

3

【分析】

---

---

【代码】

#include 
#include 
#include 
#include 
using namespace std;

typedef long long LL;
int x, y, n;

int main()
{
    cin >> x >> y;
    if (abs(x) <= y)//在上边的线上
    {
        n = y;
        cout << (LL)(2 * n - 1) * (2 * n) + x - (-n) << endl;
    }
    else if (abs(y) <= x)//在右边的线上
    {
        n = x;
        cout << (LL)(2 * n) * (2 * n) + n - y << endl;
    }
    else if (y < 0 && abs(x) <= abs(y) + 1)//在下边的线上
    {
        n = abs(y);
        cout << (LL)(2 * n) * (2 * n + 1) + n - x << endl;
    }
    else//在左边的线上
    {
        n = abs(x);
        cout << (LL)(2 * n - 1) * (2 * n - 1) + y - (-n + 1) << endl;
    }
    return 0;
}

八、AcWing 797. 差分

【题目描述】
输入一个长度为$n$的整数序列。
接下来输入$m$个操作，每个操作包含三个整数$l,r,c$，表示将序列中$[l,r]$之间的每个数加上$c$。
请你输出进行完所有操作后的序列。

【输入格式】
第一行包含两个整数$n$和$m$。
第二行包含$n$个整数，表示整数序列。
接下来$m$行，每行包含三个整数$l,r,c$，表示一个操作。

【输出格式】
共一行，包含$n$个整数，表示最终序列。

【数据范围】
$1\le n,m\le 100000$
$1\le l\le r\le n$
$-1000\le c\le 1000$
$-1000\le 整数序列中元素的值\le 1000$

【输入样例】

6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1

【输出样例】

3 4 5 3 4 2

【代码】

#include 
#include 
#include 
using namespace std;

const int N = 100010;
int a[N], b[N];
int n, m;

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) { cin >> a[i]; b[i] = a[i] - a[i - 1]; }
    while (m--)
    {
        int l, r, c;
        cin >> l >> r >> c;
        b[l] += c, b[r + 1] -= c;
    }
    for (int i = 1; i <= n; i++) { b[i] += b[i - 1]; cout << b[i] << ' '; }
    return 0;
}

九、AcWing 798. 差分矩阵

【题目描述】
输入一个$n$行$m$列的整数矩阵，再输入$q$个操作，每个操作包含五个整数$x_1,y_1,x_2,y_2,c$，其中$(x_1,y_1)$和$(x_2,y_2)$表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上$c$。
请你将进行完所有操作后的矩阵输出。

【输入格式】
第一行包含整数$n,m,q$。
接下来$n$行，每行包含$m$个整数，表示整数矩阵。
接下来$q$行，每行包含$5$个整数$x_1,y_1,x_2,y_2,c$，表示一个操作。

【输出格式】
共$n$行，每行$m$个整数，表示所有操作进行完毕后的最终矩阵。

【数据范围】
$1\le n,m\le 1000$
$1\le q\le 100000$
$1\le x_1\le x_2\le n$
$1\le y_1\le y_2\le m$
$-1000\le c\le 1000$
$-1000\le 矩阵内元素的值\le 1000$

【输入样例】

3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1

【输出样例】

2 3 4 1
4 3 4 1
2 2 2 2

【代码】

#include 
#include 
#include 
using namespace std;

const int N = 1010;
int b[N][N];
int n, m, q;

void add(int x1, int y1, int x2, int y2, int c)
{
    b[x1][y1] += c;
    b[x2 + 1][y1] -= c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

int main()
{
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
        {
            int x; scanf("%d", &x);
            add(i, j, i, j, x);
        }
    while (q--)
    {
        int x1, y1, x2, y2, c;
        scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &c);
        add(x1, y1, x2, y2, c);
    }
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
            printf("%d ", b[i][j]);
        }
        puts("");
    }
    return 0;
}