AcWing 1228. 油漆面积 线段树做法

AcWing 1228. 油漆面积

X星球的一批考古机器人正在一片废墟上考古。

该区域的地面坚硬如石、平整如镜。

管理人员为方便，建立了标准的直角坐标系。

每个机器人都各有特长、身怀绝技。

它们感兴趣的内容也不相同。

经过各种测量，每个机器人都会报告一个或多个矩形区域，作为优先考古的区域。

矩形的表示格式为 (x1,y1,x2,y2)，代表矩形的两个对角点坐标。

为了醒目，总部要求对所有机器人选中的矩形区域涂黄色油漆。

小明并不需要当油漆工，只是他需要计算一下，一共要耗费多少油漆。

其实这也不难，只要算出所有矩形覆盖的区域一共有多大面积就可以了。

注意，各个矩形间可能重叠。

输入格式
第一行，一个整数 n，表示有多少个矩形。

接下来的 n 行，每行有 4 个整数 x1,y1,x2,y2，空格分开，表示矩形的两个对角顶点坐标。

输出格式
一行一个整数，表示矩形覆盖的总面积。

数据范围
1≤n≤10000,
0≤x1,x2,y2,y2≤10000
数据保证 x1

输入样例1：

3
1 5 10 10
3 1 20 20
2 7 15 17

输出样例1：

340

输入样例2：

3
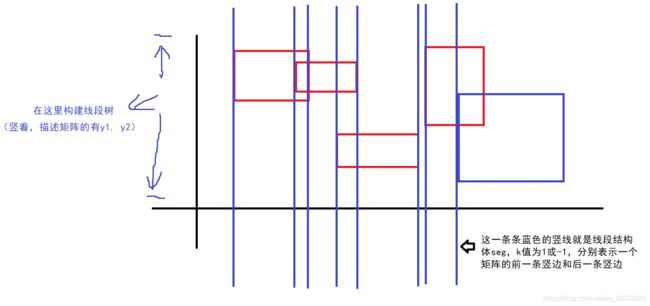
5 2 10 6
2 7 12 10
8 1 15 15

输出样例2：

128

这道题是困难难度的题，刚开始看思路还是很难想的，想着用二维树状数组，可是好像看来做不出来，我又想了用区间前缀和，我觉得也应该做不出来的，于是我就看了y总的视频我觉得y总的思路应该是区间覆盖的问题，我们先看一个图

我们对所有的x进行一个排序，每个x放的是y1,y2,以及是否放置一个区间，然后其实线段树是我们的纵坐标，我们求得是所有被覆盖的区间。线段树的操作该怎么写呢？

我们build的操作保存l,r，然后我们pushup操作
如果要是这个区间完全被覆盖了cnt>0(懒人节点)的情况，就取这个全部区间，要是没有完全被取的话
我们就取两个子树的区间和，我们需要注意一下，l==r的时候是没有子树的，我们需要格外写一个区间防止段错误，pushup的操作就是这样的，
modify的操作是什么：
几乎每个线段树都差不多，我们首先遇到完全被覆盖的区间我们就采取一个cnt>0，然后回溯的一个方式去更新一下节点的len,然后找重复的区间就去递归，不重复的就不递归了。

代码如下：

#include
#include

using namespace std;

const int N=1e4+10;

struct Seg
{
    int x1,y1,y2;
    int k;
    bool operator<(const Seg &w)
    {
        return x1;
    }
} seg[2*N];

struct Node
{
    int l,r;
    int cnt,len;//该区间被覆盖的次数。
} tr[4*N];

void pushup(int u)
{
    if(tr[u].cnt>0) tr[u].len=tr[u].r-tr[u].l+1;
    else if(tr[u].l==tr[u].r) tr[u].len=0;
    else tr[u].len=tr[u<<1].len+tr[u<<1|1].len;
}
void build(int u,int l,int r)
{
    tr[u]={l,r,0};
    if(l==r) return;
    int mid=l+r>>1;
    build(u<<1,l,mid),build(u<<1|1,mid+1,r);
}

void modify(int u,int l,int r,int k)
{
    if(tr[u].l>=l&&tr[u].r<=r)
    {
        tr[u].cnt+=k;
        pushup(u);
    }
    else
    {
        int mid=tr[u].l+tr[u].r>>1;
        if(l<=mid) modify(u<<1,l,r,k);
        if(r>mid) modify(u<<1|1,l,r,k);
        pushup(u);
    }
}

int main(void)
{
    int n;
    scanf("%d",&n);
    int m=0;
    for(int i=1;i<=n;i++)
    {
        int x1,y1,x2,y2;
        scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
        seg[m++]={x1,y1,y2,1};
        seg[m++]={x2,y1,y2,-1};
    }
    sort(seg,seg+m);
    build(1,0,10000);
    long long res=0;
    for(int i=0;i;i++)
    {
        if(i) res+=tr[1].len*(seg[i].x1-seg[i-1].x1);
        modify(1,seg[i].y1,seg[i].y2-1,seg[i].k);
    }
    cout<;
}