用于非线性时间序列预测的稀疏局部线性和邻域嵌入（Matlab代码实现）

‍ 个人主页： 研学社的博客

欢迎来到本博客 ❤️ ❤️


博主优势： 博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。


⛳ 座右铭：行百里者，半于九十。

本文目录如下：
目录
1 概述
2 运行结果
3 参考文献
4 Matlab代码实现

1 概述

“本文提出了一种基于字典的L1范数稀疏编码，用于时间序列预测，不需要训练阶段，参数调整最少，适用于非平稳和在线预测应用。预测过程被表述为基础追求 L1 范数问题，其中为每个测试向量估计一组稀疏权重。尝试了约束稀疏编码公式，包括稀疏局部线性嵌入和稀疏最近邻嵌入。16个时间序列数据集用于测试离线时间序列预测方法，其中训练数据是固定的。所提出的方法还与Bagging树（BT），最小二乘支持向量回归（LSSVM）和正则化自回归模型进行了比较。所提出的稀疏编码预测显示出比使用10倍交叉验证的LSSVM更好的性能，并且比正则化AR和Bagging树的性能明显更好。平均而言，在LSSVM训练时可以完成几千个稀疏编码预测。

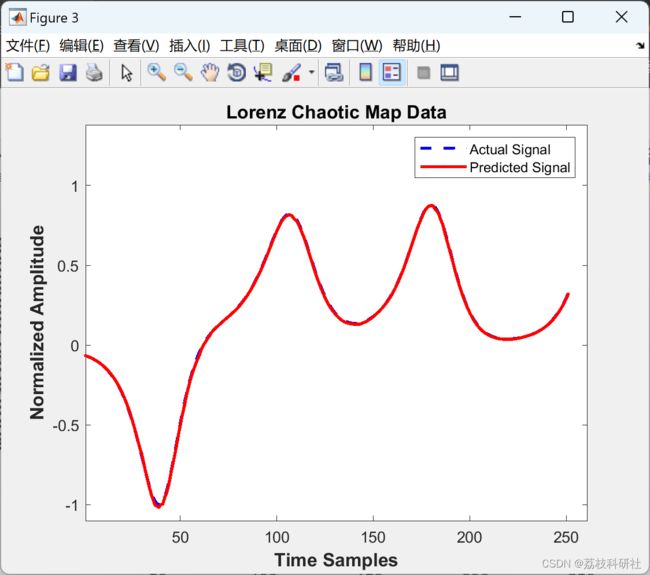
2 运行结果

部分代码：

clear all;

%Time series Prediction using Sparse coding with overcomplete dictionaries

%In each case, the test data prediction is plotted versus the real data

%and the sparsity of the solution is recorded.

%both L1-magic (if LASSO=0) and CVX libraries (if LASSO=1) must be included

% in the Matlab path

%if normalize=1 use sqrt(x*x'), normalize=2 use st.dev., normalize=3 use

%the L1 norm, or zero then no normalization.

normalize1=2;

normalize2=2;

eps=0.001; %the error constraint

thr=0.001; %the pruning threshold

NN=20000; %these are the max number of neighbors allowed

dthr=0.0; %the distance threshold used to filter the dictionary. If it

%is zero then no dictionary filtering is done

LASSO=1; %0 for BP and 1 for BPDN or LASSO using CVX

for kkk=1:16 %The 16 data sets used for evaluation

nnnn=kkk;

if(nnnn==1) %Mackey-Glass data

load MGData;

a = MGData;

time = a(:, 1);

x_t = a(:, 2);

trn_data = zeros(500, 5);

chk_data = zeros(500, 5);

time = 1:sz;

Train = x_t(1:100);

Test = x_t(101:190);

K=6;

eps=0.001;

C = 'USD-EURO Data'

elseif(nnnn==15)

load IkedaData1; %Z-normalized

if(nonorm==1)

for i=1:L1-K

dzz(i)=1;

end

end

end

%Now we normalize the targets of the training data

for i=1:L1-K

if(normalize1==5)

T(i) = (trg1(i)-dmm(i))/dvv(i);

else

T(i) = trg1(i)/dzz(i);

end

end

TR = T;

%%%%%%%%This is the dictionary filtering process (if we want to reduce the

%%%%%%%%number of similar atoms. It is controlled by the dthr value

%%%%%%%%specified by the user. I have not investigated this a lot

dictsize=size(DD);

nn=dictsize(1); %the large dimension

mm=dictsize(2); %the small dimension

RR=randn(nn,mm);

RR=orth(RR);

tooclose=0;

for io=1:nn %over all the atoms

xio = DD(io,1:mm);

cnt=0;

for jo= io+1 : nn

dddd(jo) = dist(xio,DD(jo,1:mm)');

if(dddd(jo) <= dthr) cnt=cnt+1; %one or more atoms are too close

end

end

if(io

mindist(io) = min(dist(xio,DD(io+1:nn,1:mm)')); %the min distance for each atom with the next ones

else

mindist(io)=0;

end

if(cnt==0) %no atoms are too close

FF(io,1:mm) = DD(io,1:mm);

FT(io) = TR(io);

else %some atoms are too close, so we remove this one and put a random atom

FF(io,1:mm) = RR(io, 1:mm);

FT(io) = 0; %the target for the random atoms is zero

tooclose=tooclose+1;

end

end

%So, now the new dictionary is FF and the new targets is FT

%(if no filtering happened then FF is the same as DD)

TooClose(kkk) = tooclose; %this will tell us how many atoms were replaced (removed)

MinDist(kkk,1:nn)=mindist(1:nn);

%here we construct the test data

Test(1:(L2-K),1:K) = tst(1:(L2-K),1:K);

TT = trg2(1:(L2-K));

M=L2-K;

tic %to get the test time

sprs=0; %to accumulate the sparsity over test vectors

for i=1:M %loop over M vectors from the test data

disp('**************');

disp(i);

test(1:K) = Test(i,1:K);

%here we normalize the test vector by its own dot product

if(normalize2==1) normtest = sqrt(test*test');

elseif(normalize2==2) normtest = sqrt(var(test));

elseif(normalize2==3) normtest = norm(test,1);

elseif(normalize2==0) normtest=1;

end

3 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]Waleed Fakhr, "Sparse Locally Linear and Neighbor Embedding for Nonlinear Time Series Prediction", ICCES 2015, December 2015.

4 Matlab代码实现