动态规划 (Python Code)
动态规划
- 01背包问题
- 钢条切割问题
- 数字三角形问题
- 最长公共子序问题
- 最长上升子序列问题
01背包问题
问题描述:
给定n个物品和一个容量为C的背包,物品i的重量是Wi,其价值为Vi,背包问题是如何选择入背包的物品,使得装入背包的物品的总价值最大。
不能重复装,物品不可拆分
代码实现:
def dsf(n,total_weight):
if(total_weight == 0): return 0
if(n == 0): return 0
if(w[n-1] > total_weight):
return dsf(n-1,total_weight)
else:
return max(v[n-1]+dsf(n-1,total_weight-w[n-1]),dsf(n-1,total_weight))
w = [2,1,3,2]
v = [3,2,4,2]
n = 4
total_weight = 5
print(dsf(n,total_weight))
钢条切割问题
问题描述:
某公司出售钢条,出售价格与钢条长度之间的关系如下表:

问题:现有一段长度为n的钢条和上面的价格表,求切割钢条方案,使得总收益最大。
代码实现:
def cut_rod_recurision(price,length):
if length==0:
return 0
else:
res=0
for i in range(1,length+1):
res=max(res,price[i]+cut_rod_recurision(price,length-i))
return res
if __name__=="__main__":
price=[0,1,5,8,9,10,17,17,20,24,30]
print(cut_rod_recurision(price,9))
总结:
设长度为n的钢条切割后最优收益值为rn,可以得出递推式:
rn=max(pn,r1+rn−1,r2+rn−2,…,rn−1十r1)
可以将求解规模为n的原问题,划分为规模更小的子问题,完成一次切割后,可以将产生的两端钢条看成两个独立的钢条切割问题。
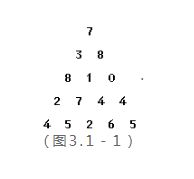
数字三角形问题
问题描述:
示出了一个数字三角形。 请编一个程序计算从顶至底的某处的一条路
径,使该路径所经过的数字的总和最大。
●每一步可沿左斜线向下或右斜线向下走;
●1<三角形行数≤100;
●三角形中的数字为整数0,1,…99;
代码实现:
n = int(input())
s = []
for i in range(n):
s.append(list(map(int,input().split())))
def dfs(i,j):
if(i > n-1 or j > n-1): return 0
if(i<=n-1):
dpn = s[i][j]+max(dfs(i+1,j),dfs(i+1,j+1))
return dpn
print(dfs(0,0))
总结:
对于当前的数字来说,他只有选择下面(行+1,列不变) 或者 右下角(行+1,列+1)
把问题又进一步分成 一个小问题。重复递归 求取最大值。
最长公共子序问题
def LCS(string1,string2):
len1 = len(string1)
len2 = len(string2)
res = [[0 for i in range(len1+1)] for j in range(len2+1)]
#python 初始化二维数组 [len2+1],[len1+1]
for i in range(1,len2+1): #开始从1开始,到len2+1结束
for j in range(1,len1+1): #开始从1开始,到len2+1结束
if string2[i-1] == string1[j-1]:
res[i][j] = res[i-1][j-1]+1
else:
res[i][j] = max(res[i-1][j],res[i][j-1])
return res,res[-1][-1] #返回res[len2+1][len1+1]
print(LCS("helloworld","loop"))
# 输出结果为:
[[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1],
[0, 0, 0, 1, 1, 2, 2, 2, 2, 2, 2],
[0, 0, 0, 1, 1, 2, 2, 3, 3, 3, 3],
[0, 0, 0, 1, 1, 2, 2, 3, 3, 3, 3]], 3
因此可以根据这个方程来进行填表,以"helloworld"和“loop”为例:
最长上升子序列问题
问题描述:
给定一个长度为N的数列,求数值严格单调递增的子序列的长度最长是多少。
输入格式
第一行包含整数N。
第二行包含N个整数,表示完整序列。
输出格式
输出一个整数,表示最大长度。
数据范围
1≤N≤1000,
−109≤数列中的数≤109
输入样例:
7
3 1 2 1 8 5 6
代码实现:
n = int(input())
nums = list(map(int, input().split()))
dp = [1]*(n)
res = 1
for i in range(1, n): #判断以 nums[i] 结尾的最长子序列
for j in range(i):
if nums[j] < nums[i]:
dp[i] = max(dp[i], dp[j]+1) # dp[i] 表示的就是 以sums[i] 结尾的最长子序列
res = max(res, dp[i])
print(res)
总结:
先写出DP方程 dp[i] = max(dp[i],dp[j]+1)



