kaggle房价预测得分
In recent months Florian Wetschoreck published a story on Toward Data Science’s Medium channel that attracted the attention of many data scientists on LinkedIn thanks to its very provocative title: “RIP correlation. Introducing the Predictive Power Score”. Let’s see what it is and how to use it in R.
最近几个月, Florian Wetschoreck在Toward Data Science的Medium频道上发表了一个故事,该故事因其非常具有启发性的标题: “ RIP相关性”而吸引了LinkedIn上许多数据科学家的关注。 介绍预测能力得分” 。 让我们看看它是什么以及如何在R中使用它。
预测能力得分的定义 (Definition of Predictive Power Score)
The Predictive Power Score (PPS) is a normalized index (it ranges from 0 to 1) that tells us how much the variable x (be it numerical or categorical) could be used to predict the variable y (numerical or categorical). The higher the PPS index, the more the variable x is decisive in predicting the variable y.
预测能力得分 (PPS)是归一化的索引(范围从0到1),它告诉我们变量x (无论是数值还是分类的)可以用来预测变量y (数值或分类的)多少。 PPS指数越高,变量x对预测变量y的决定性就越大。
The conceptual similarity of PPS with the correlation coefficient is evident, although the following differences exist:
尽管存在以下差异,但PPS在概念上与相关系数的相似性是显而易见的:
PPS also detects non-linear relationships between x and y.
PPS还检测x和y之间的非线性关系。
PPS is not a symmetrical index. This means that PPS(x, y) ≠ PPS(y, x). In other words, it is not said that if x predicts y, then y also predicts x.
PPS不是对称索引。 这意味着PPS( x , y )≠PPS( y , x )。 换句话说,并不是说如果x预测y ,那么y也会预测x 。
- PPS allows both numerical and categorical variables. PPS允许数值和分类变量。
Basically, PPS is an asymmetric nonlinear index that is applicable to all types of variables for predictive purposes.
基本上,PPS是非对称非线性指标,出于预测目的,它适用于所有类型的变量。
Behind the scene it implements Decision Trees as learning algorithms due to their robustness to outliers and poor data pre-processing.
由于其对异常值的鲁棒性和不良的数据预处理,在后台将决策树实现为学习算法。
The score is calculated on the test sets of a default of 4-fold cross-validation given by the scikit-learn cross_val_score function and it is given by different metrics according to the type of problem (regression or classification) defined by the target variable:
分数是根据scikit-learn cross_val_score函数给出的默认4倍交叉验证的测试集计算得出的,并且根据目标变量定义的问题类型( 回归或分类 )由不同的指标给出:
Regression: Mean Absolute Error (MAE) normalized to the [0, 1] interval given a baseline of “naïve” values of y calculated as the median of the target variable.
回归 :归一化为[0,1]区间的平均绝对误差(MAE),给定y的“天真”值基线作为目标变量的中值。
Classification: Weighted F1 normalized to the [0, 1] interval given a baseline of “naïve” values of y calculated as the most common value of the target variable or a random value (sometimes, a random value has a higher F1 than the most common value).
分类 :加权的F1归一化为[0,1]区间,给定y的“初始”值基线作为目标变量的最常见值或随机值(有时,随机值的F1高于最高值)共同价值)。
You can get into the details of the Python code thanks to the fact that the Predictive Power Score project was released as open source on Github.
由于Predictive Power Score项目已在Github上作为开源发布,您可以深入了解Python代码的细节。
皮尔逊相关与PPS (Pearson Correlation vs PPS)
The two indexes come from different domains and fundamental distinctions must be made:
这两个索引来自不同的领域,必须进行基本的区分:
Pearson correlation is given by the normalized covariance between two numerical variables. Covariance depends on the deviations of the two variables from their respective means, so it’s a statistical measure. Given two numerical variables, Pearson correlation is a descriptive index well defined mathematically that gives the goodness-of-fit for the best possible linear function describing the relation between the variables.
皮尔逊相关性由两个数值变量之间的归一化协方差给出。 协方差取决于两个变量与其各自平均值的偏差,因此这是一种统计量度。 给定两个数值变量,Pearson相关性是数学上定义良好的描述性索引,可为描述变量之间关系的最佳线性函数提供拟合优度。
PPS tries to solve the issues of only linear correlations and only numeric variables being measured in a correlation analysis by applying decision tree estimation. It is derived from performance metrics of that estimation. At the time this post was written (version 1.1.0), it gets by default a random sample (stratified if needed) of 5000 rows from the input dataset in order to speed up the calculations (the size of the sample can be modified using a proper parameter). No tuning is done to get the optimal model parameters for the decision tree. There is therefore the possibility of overfitting or underfitting. Moreover, PPS results could be different at each run over the same dataset due to the randomness inherent to the algorithm (random seed could be used to guarantee the reproducibility of results). So, PPS could be inaccurate. But its aim is not to give an exact score, rather the general notion of dependency and a fast result.
PPS试图通过应用决策树估计来解决仅线性相关和相关分析中仅测量数值变量的问题。 它是从该估算的性能指标得出的。 在撰写本文时(版本1.1.0),默认情况下会从输入数据集中获取5000行的随机样本(如有需要,进行分层),以加快计算速度(样本大小可以使用适当的参数)。 没有进行调整以获得决策树的最佳模型参数。 因此,可能会过度拟合或拟合不足。 此外,由于算法固有的随机性,每次运行PPS结果在同一数据集上可能会有所不同(随机种子可用于保证结果的可重复性)。 因此,PPS可能不准确。 但是其目的不是给出确切的分数,而是给出依赖和快速结果的一般概念。
Both the indexes should be used during the Exploration Data Analysis phase. As the same author says:
这两个索引都应在“勘探数据分析”阶段使用。 正如同一位作者所说:
The PPS clearly has some advantages over correlation for finding predictive patterns in the data. However, once the patterns are found, the correlation is still a great way of communicating found linear relationships.
对于在数据中查找预测模式 ,PPS显然比相关性具有一些优势。 但是,一旦找到模式,相关性仍然是传达找到的线性关系的一种好方法。
PPS用例 (PPS Use Cases)
The author lists several use cases in his article where PPS may add value:
作者在他的文章中列出了PPS可以增加价值的几个用例:
- Finds every relationship that the correlation finds and more 查找关联找到的每个关系以及更多
- Feature selection 功能选择
- Detect information leakage 检测信息泄漏
- Find entity structures in the data via interpreting the PPS matrix as a directed graph. 通过将PPS矩阵解释为有向图,在数据中查找实体结构。
如何在自己的R项目中使用PPS (How to use the PPS in your own R project)
As mentioned before, the project ppscore is open sourced and it’s developed in Python. There is currently no porting project of ppscore in R. So how to use the ppscore functions in an R script? It’s possible to use the prowess of R along with the programming capabilities of Python and vice-versa thanks to some libraries created for interoperability between Python and R. Among the others, two of them are the most widely used:
如前所述,项目ppscore是开源的,它是用Python开发的。 R中目前没有ppscore的移植项目。那么如何在R脚本中使用ppscore函数? 得益于为Python和R之间的互操作性而创建的一些库,可以结合使用R的强大功能和Python的编程功能,反之亦然。在其他两个库中,其中两个使用最为广泛:
rpy2: an interface to R running embedded in a Python process
rpy2:嵌入在Python进程中的R运行接口
reticulate: a comprehensive set of tools for interoperability between Python and R thanks to embedded session of Python within R sessions
网状结构:由于Python在R会话中的嵌入式会话,因此提供了一套全面的工具来实现Python和R之间的互操作性
In our scenario, reticulate will allow ppscore functions to be called from an R script.
在我们的方案中, 网状结构允许从R脚本调用ppscore函数。
为ppscore准备一个单独的Python环境 (Prepare a separated Python environment for ppscore)
First of all, if you didn’t install Python on your machine, I suggest to install Miniconda (a small, bootstrap version of Anaconda that includes only conda, Python, and few other useful packages), letting the installer add the Python installation path to your PATH environment variable in case of a Windows machine.
首先,如果您没有在计算机上安装Python,建议安装Miniconda (Anaconda的小型引导程序版本,仅包含conda,Python和其他一些有用的软件包),让安装程序添加Python安装路径如果是Windows计算机,则将其设置为PATH环境变量。
Python developers usually use virtual environments. A virtual environment is a tool that helps to keep dependencies required by different projects separated by creating self-contained directory trees that contain Python installations for particular versions of Python, plus a number of additional packages. Conda is a tool that helps to manage environments and packages.
Python开发人员通常使用虚拟环境。 虚拟环境是一种工具,可通过创建自包含目录树来保持不同项目所需的依赖关系,这些目录树包含针对特定版本的Python的Python安装以及许多其他软件包。 Conda是有助于管理环境和程序包的工具。
In this case a new Python environment will be created in order to install the ppscore required packages on it. You can use the following R script to prepare a new Python environment for the ppscore library:
在这种情况下,将创建一个新的Python环境,以便在其上安装ppscore所需的软件包。 您可以使用以下R脚本为ppscore库准备新的Python环境:
# Install reticulate
if( !require(reticulate) ) {
install.packages("reticulate")
}# Load reticulate
library(reticulate)# List current python environments
conda_list()# Create a new environemnt called 'test_ppscore'
conda_create(envname = "test_ppscore")# Install the ppscore package and its dependencies using pip into the test_ppscore environment.
# Requirements are listed here: https://github.com/8080labs/ppscore/blob/master/requirements.txt
conda_install(envname = "test_ppscore", packages = "pandas", pip = TRUE)
conda_install(envname = "test_ppscore", packages = "scikit-learn", pip = TRUE)
conda_install(envname = "test_ppscore", packages = "ppscore", pip = TRUE)# Check if the new environment is now listed
conda_list()# Make sure to use the new environment
use_condaenv("test_ppscore")# Import the ppscore Python module in your R session
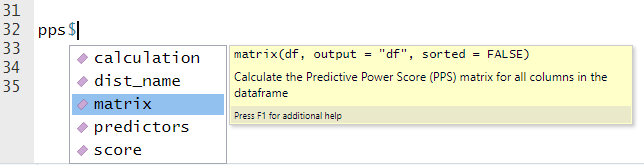
pps <- import(module = "ppscore")Functions and other data within Python modules and classes can be accessed via the $ operator (as well as interacting with an R list). Imported Python modules support code completion and inline help. For example, the matrix function in the pps module can be accessed as follows:
可以通过$运算符(以及与R列表进行交互)访问Python模块和类中的函数和其他数据。 导入的Python模块支持代码完成和内联帮助。 例如,可以按以下方式访问pps模块中的matrix函数:
If you want to learn more about reticulate, you can go through its home page.
如果要了解有关网状结构的更多信息,可以浏览其主页 。
适用于Titanic预测变量和变量重要性的PPScore热图 (PPScore Heatmap for Titanic’s predictors and Variable Importance)
Starting from the example the author included in the repository, it’s possible to replicate the Titanic PPScore Heatmap using the matrix function:
从存储库中包含作者的示例开始,可以使用matrix函数复制Titanic PPScore Heatmap:
The Variable Importance given the target “Survived” is obtainable filtering properly the output (complete interaction between predictors) given by the matrix function. But it is also possible to use directly the predictor function to directly have the same result, being careful to use the same random_seed parameter within both functions, in order to avoid to obtain different results.
给定目标“生存”的变量重要性可正确过滤matrix函数给定的输出(预测变量之间的完全相互作用)。 但是也有可能直接使用predictor函数直接获得相同的结果,请小心在两个函数中使用相同的random_seed参数,以避免获得不同的结果。
The Variable Importance plot given the target variable “Survived” is the following:
给定目标变量“生存”的变量重要性图如下:
The R code used to get the above plots is the following:
用于获得上述曲线的R代码如下:
library(reticulate)
library(readr)
library(dplyr)
library(ggplot2)heatmap <- function(df, x, y, value,
main_title = "Heatmap", legend_title = "Value",
x_title = "feature", y_title = "target") {
x_quo <- enquo(x)
y_quo <- enquo(y)
value_quo <- enquo(value)
res <- ggplot( df, aes(x = !!x_quo, y = !!y_quo, fill = !!value_quo) ) +
geom_tile(color = "white") +
scale_fill_gradient2(low = "white", high = "steelblue",
limit = c(0,1), space = "Lab",
name="PPScore") +
theme_minimal()+ # minimal theme
# theme(axis.text.x = element_text(angle = 45, vjust = 1,
# size = 12, hjust = 1)) +
coord_fixed() +
geom_text(aes(x, y, label = round(!!value_quo, 2)), color = "black", size = 4) +
theme(
axis.text.x = element_text(angle = 45, vjust = 1,
size = 12, hjust = 1),
axis.text.y = element_text(size = 12),
panel.grid.major = element_blank(),
panel.border = element_blank(),
panel.background = element_blank(),
axis.ticks = element_blank()
) +
xlab(x_title) +
ylab(y_title) +
labs(fill = legend_title) +
guides(fill = guide_colorbar(barwidth = 1, barheight = 10,
title.position = "top", title.hjust = 1)) +
ggtitle(main_title)
return(res)
}lollipop <- function(df, x, y,
main_title = "Variable Importance",
x_title = "PPScore", y_title = "Predictors",
caption_title = "Data from Titanic dataset") {
x_quo <- enquo(x)
y_quo <- enquo(y)
res <- ggplot(df, aes(x=!!x_quo, y=forcats::fct_reorder(!!y_quo, !!x_quo, .desc=FALSE))) +
geom_segment( aes(x = 0,
y=forcats::fct_reorder(!!y_quo, !!x_quo, .desc=FALSE),
xend = !!x_quo,
yend = forcats::fct_reorder(!!y_quo, !!x_quo, .desc=FALSE)),
color = "gray50") +
geom_point( color = "darkorange" ) +
labs(x = x_title, y = y_title,
title = main_title,
#subtitle = "subtitle",
caption = caption_title) +
theme_minimal() +
geom_text(aes(label=round(!!x_quo, 2)), hjust=-.5, size = 3.5
) +
theme(panel.border = element_blank(),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
axis.line = element_blank(),
axis.text.x = element_blank())
return(res)
}df <- read_csv("https://raw.githubusercontent.com/8080labs/ppscore/master/examples/titanic.csv")df <- df %>%
mutate( Survived = as.factor(Survived) ) %>%
mutate( across(where(is.character), as.factor) ) %>%
select(
Survived,
Class = Pclass,
Sex,
Age,
TicketID = Ticket,
TicketPrice = Fare,
Port = Embarked
)use_condaenv("test_ppscore")pps <- import(module = "ppscore")# PPScore heatmap
score <- pps$matrix(df = df, random_seed = 1234L)score %>% heatmap(x = x, y = y, value = ppscore,
main_title = "PPScore for Titanic's predictors", legend_title = "PPScore")# Variable importance
vi <- pps$predictors( df = df, y = "Survived", random_seed = 1234L)vi %>%
mutate( x = as.factor(x) ) %>%
lollipop( ppscore, x,
main_title = "Variable Importance for target = 'Survived'",
x_title = "PPScore", y_title = "Predictors",
caption_title = "Data from Titanic dataset")PPS与各种分布的相关性 (PPS and Correlation against various distributions)
Denis Boigelot published a quite famous picture about Pearson correlation examples on Wikimedia Commons, sharing also the R code used to get this picture:
Denis Boigelot在Wikimedia Commons上发布了有关Pearson相关示例的非常著名的图片,还共享了用于获取此图片的R代码:
Starting from that code, it’s possible to calculate the PPScore for the same distributions. Here the results for X→Y:
从该代码开始,可以为相同的分布计算PPScore。 这里X→Y的结果:
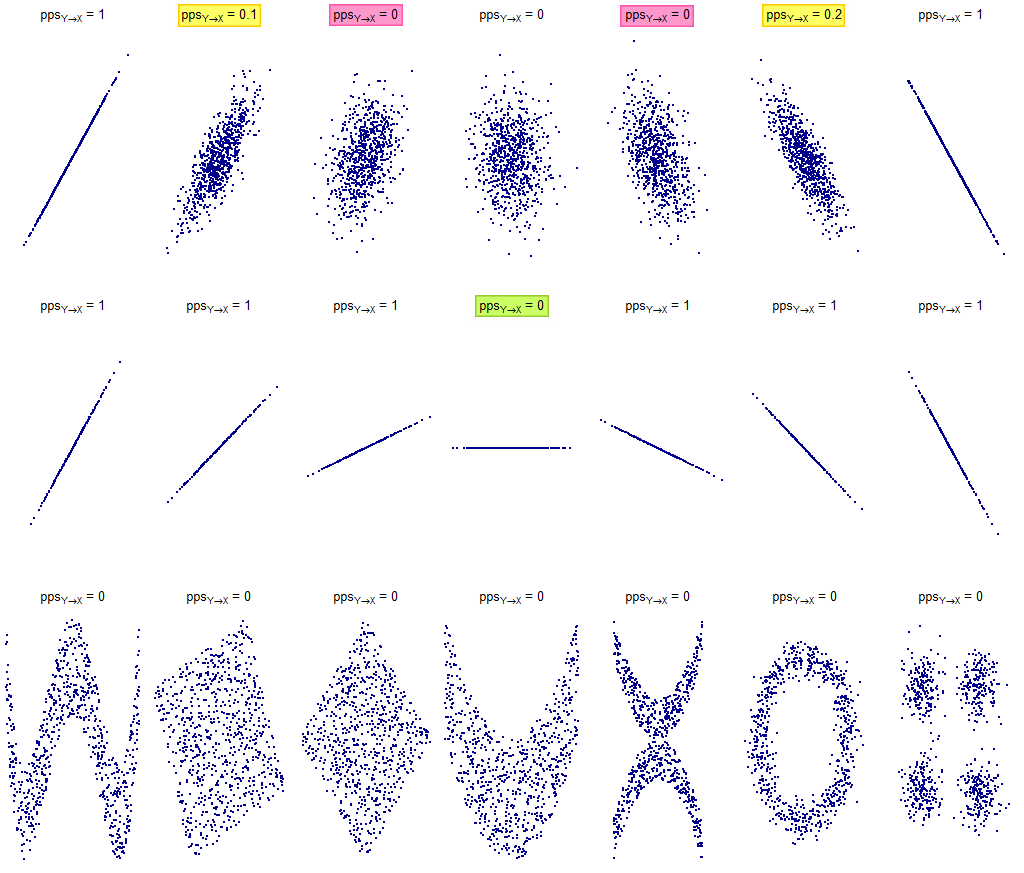
Here the results for Y→X:
以下是Y→X的结果:
fig. 7 — PPScore for “y predicts x” over the Boigelot distributions 图。 7 —在Boigelot分布上用于“ y预测x”的PPScoreIt’s clear that at the time this post was written
很明显,在撰写本文时
PPScore struggles to identify linear relationships in presence of even minimal dispersion of the points from the line of origin (as highlighted in yellow and red in previous pictures).
PPScore很难在直线与原点之间存在最小分散的情况下识别线性关系(如上图中以黄色和红色突出显示)。
These cases show
这些情况表明
how important it is also to use a correlation index to check linearity in order not to run into wrong conclusions.
为了避免得出错误的结论,使用相关指数检查线性也很重要。
I shared these results with the author and he confirmed they are studying a solution to solve linear relationships issues. He also shared the reasons why PPScore 1.1.0 doesn’t work well with linear relationships at this link.
我与作者分享了这些结果,他确认他们正在研究解决线性关系问题的解决方案。 他还分享了PPScore 1.1.0 在此链接上与线性关系不能很好地工作的原因。
Conversely, PPScore provides good results on some distributions for which Pearson correlation was not sufficient (as highlighted in green in previous pictures).
相反,PPScore在某些皮尔逊相关性不足的分布上提供了良好的结果(如上图中绿色突出显示)。
The R code used to get the above Boigelot distributions is the following:
用于获取上述Boigelot分布的R代码如下:
# Install packages
pkgs <- c("dplyr","ggplot2","ggpubr","mvtnorm")for (pkg in pkgs) {
if (! (pkg %in% rownames(installed.packages()))) { install.packages(pkg) }
}# Load packages
library(mvtnorm)
library(dplyr)
library(ggplot2)
library(ggpubr)
library(reticulate)# Functions
MyPlot <- function(xy, xlim = c(-4, 4), ylim = c(-4, 4), eps = 1e-15,
metric = c("cor", "ppsxy", "ppsyx")) {
metric <- metric[1]
df <- as.data.frame(xy)
names(df) <- c("x", "y")
if (metric == "cor") {
value <- round(cor(xy[,1], xy[,2]), 1)
if (sd(xy[,2]) < eps) {
#title <- bquote("corr = " * "undef") # corr. coeff. is undefined
title <- paste0("corr = NA") # corr. coeff. is undefined
} else {
#title <- bquote("corr = " * .(value))
title <- paste0("corr = ", value)
}
subtitle <- NULL
} else if (metric == "ppsxy") {
pps_df <- pps$matrix(df = df, random_seed = 1111L)
value <- pps_df %>%
filter( x == "x" & y == "y" ) %>%
mutate( ppscore = round(ppscore, 1) ) %>%
pull(ppscore)
title <- bquote("pps"[X%->%Y] * " = " * .(value))
subtitle <- NULL
} else if (metric == "ppsyx") {
pps_df <- pps$matrix(df = df, random_seed = 1111L)
value <- pps_df %>%
filter( x == "y" & y == "x" ) %>%
mutate( ppscore = round(ppscore, 1) ) %>%
pull(ppscore)
title <- bquote("pps"[Y%->%X] * " = " * .(value))
subtitle <- NULL
}
ggplot(df, aes(x, y)) +
geom_point( color = "darkblue", size = 0.2 ) +
xlim(xlim) +
ylim(ylim) +
labs(title = title,
subtitle = subtitle) +
theme_void() +
theme( plot.title = element_text(size = 10, hjust = .5) )
}MvNormal <- function(n = 1000, cor = 0.8, metric = c("cor", "ppsxy", "ppsyx")) {
metric <- metric[1]
res <- list()
j <- 0
for (i in cor) {
sd <- matrix(c(1, i, i, 1), ncol = 2)
x <- rmvnorm(n, c(0, 0), sd)
j <- j + 1
name <- paste0("p", j)
res[[name]] <- MyPlot(x, metric = metric)
}
return(res)
}rotation <- function(t, X) return(X %*% matrix(c(cos(t), sin(t), -sin(t), cos(t)), ncol = 2))RotNormal <- function(n = 1000, t = pi/2, metric = c("cor", "ppsxy", "ppsyx")) {
metric <- metric[1]
sd <- matrix(c(1, 1, 1, 1), ncol = 2)
x <- rmvnorm(n, c(0, 0), sd)
res <- list()
j <- 0
for (i in t) {
j <- j + 1
name <- paste0("p", j)
res[[name]] <- MyPlot(rotation(i, x), metric = metric)
}
return(res)}Others <- function(n = 1000, metric = c("cor", "ppsxy", "ppsyx")) {
metric <- metric[1]
res <- list()
x <- runif(n, -1, 1)
y <- 4 * (x^2 - 1/2)^2 + runif(n, -1, 1)/3
res[["p1"]] <- MyPlot(cbind(x,y), xlim = c(-1, 1), ylim = c(-1/3, 1+1/3), metric = metric)
y <- runif(n, -1, 1)
xy <- rotation(-pi/8, cbind(x,y))
lim <- sqrt(2+sqrt(2)) / sqrt(2)
res[["p2"]] <- MyPlot(xy, xlim = c(-lim, lim), ylim = c(-lim, lim), metric = metric)
xy <- rotation(-pi/8, xy)
res[["p3"]] <- MyPlot(xy, xlim = c(-sqrt(2), sqrt(2)), ylim = c(-sqrt(2), sqrt(2)), metric = metric)
y <- 2*x^2 + runif(n, -1, 1)
res[["p4"]] <- MyPlot(cbind(x,y), xlim = c(-1, 1), ylim = c(-1, 3), metric = metric)
y <- (x^2 + runif(n, 0, 1/2)) * sample(seq(-1, 1, 2), n, replace = TRUE)
res[["p5"]] <- MyPlot(cbind(x,y), xlim = c(-1.5, 1.5), ylim = c(-1.5, 1.5), metric = metric)
y <- cos(x*pi) + rnorm(n, 0, 1/8)
x <- sin(x*pi) + rnorm(n, 0, 1/8)
res[["p6"]] <- MyPlot(cbind(x,y), xlim = c(-1.5, 1.5), ylim = c(-1.5, 1.5), metric = metric)
xy1 <- rmvnorm(n/4, c( 3, 3))
xy2 <- rmvnorm(n/4, c(-3, 3))
xy3 <- rmvnorm(n/4, c(-3, -3))
xy4 <- rmvnorm(n/4, c( 3, -3))
res[["p7"]] <- MyPlot(rbind(xy1, xy2, xy3, xy4), xlim = c(-3-4, 3+4), ylim = c(-3-4, 3+4), metric = metric)
return(res)
}output <- function( metric = c("cor", "ppsxy", "ppsyx") ) {
metric <- metric[1]
plots1 <- MvNormal( n = 800, cor = c(1.0, 0.8, 0.4, 0.0, -0.4, -0.8, -1.0), metric = metric );
plots2 <- RotNormal(200, c(0, pi/12, pi/6, pi/4, pi/2-pi/6, pi/2-pi/12, pi/2), metric = metric);
plots3 <- Others(800, metric = metric)
ggarrange(
plots1$p1, plots1$p2, plots1$p3, plots1$p4, plots1$p5, plots1$p6, plots1$p7,
plots2$p1, plots2$p2, plots2$p3, plots2$p4, plots2$p5, plots2$p6, plots2$p7,
plots3$p1, plots3$p2, plots3$p3, plots3$p4, plots3$p5, plots3$p6, plots3$p7,
ncol = 7, nrow = 3
)
}#-- Main -------------------------------------
use_condaenv("test_ppscore")pps <- import(module = "ppscore")output( metric = "cor" )
output( metric = "ppsxy" )
output( metric = "ppsyx" )结论 (Conclusions)
The Predictive Power Score (PPS) index proposed by Florian Wetschoreck tries to help data scientists in giving a hint to find any kind of relationship between two variables during the EDA phase of a project, being them numerical or categorical. PPS could be inaccurate, but its aim is not to give an exact score, rather the general notion of dependency between two variables and a fast result.
Florian Wetschoreck提出的预测能力得分(PPS)指数旨在帮助数据科学家提供暗示,以发现在项目的EDA阶段两个变量之间的任何类型的联系,无论这些变量是数字的还是分类的。 PPS可能不准确,但其目的不是给出准确的分数,而是给出两个变量之间的依存关系和快速结果的一般概念。
Using the Boigelot distributions, it was shown that PPS (the current version is 1.1.0) is able to identify non-linear relationships not identified by the correlation index. Conversely, PPS seems to struggle to identify linear relationships in presence of even minimal dispersion of the points from the line of origin.
使用Boigelot分布,可以证明PPS(当前版本为1.1.0)能够识别未由相关指数识别的非线性关系。 相反,PPS似乎很难识别线性关系,即使这些点与原点线之间的分散很小。
Although PPScore was developed in Python, its functions can also be used in an R script thanks to reticulate.
尽管PPScore是用Python开发的,但由于reticulate ,其功能也可以在R脚本中使用。
All the code can be found on this Github repository.
所有代码都可以在这个Github仓库中找到。
翻译自: https://towardsdatascience.com/using-the-predictive-power-score-in-r-26c43d05dc01
kaggle房价预测得分