数据结构-交换排序：（冒泡排序和快速排序）

1.冒泡排序

1.排序思路

冒泡排序称之为气泡排序，是一种典型的交换排序方法，其基本思想是通过无序区中相邻元素的值的比较和位置的交换使值最大的元素如气泡一样逐渐往上“漂浮”直至水面。
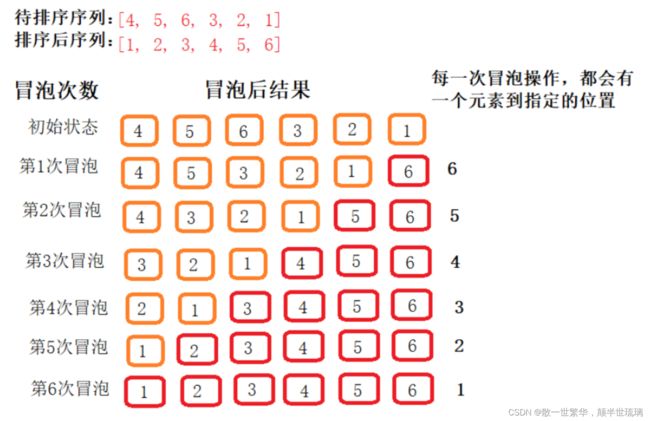
核心思想：假设待排序序列有n个元素，需要经过n-1次冒泡，每一次冒泡过程中依次比较交换相邻的两个元素，一次冒泡结束，都会有1个元素到达指定的目标位置。
具体实现步骤如下所示：
1.比较相邻的元素。如果第一个比第二个大，就交换他们两个。
2.对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。
3.针对所有的元素重复以上的步骤，除了最后一个。
4.持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。
具体的过程如下图所示：对数组[4,5,6,3,2,1]进行冒泡排序

为了加深读者们的理解，这里在配一个GIF动图演示，具体如下：

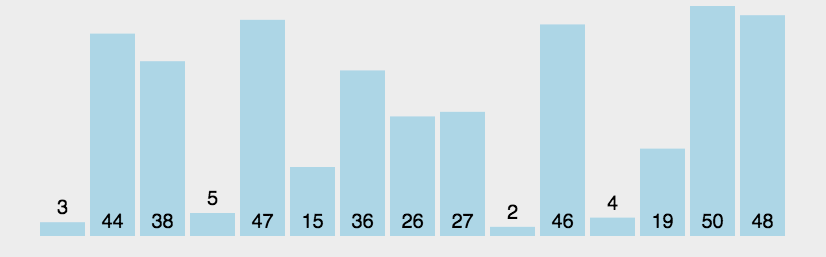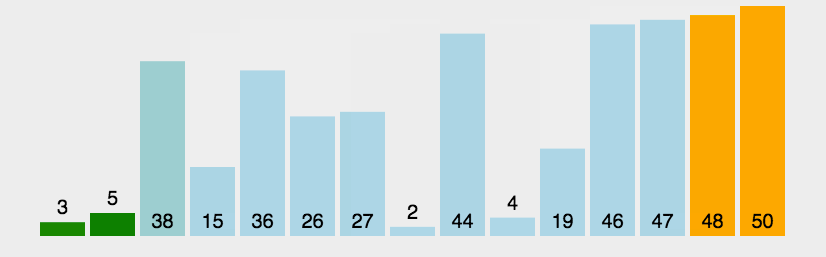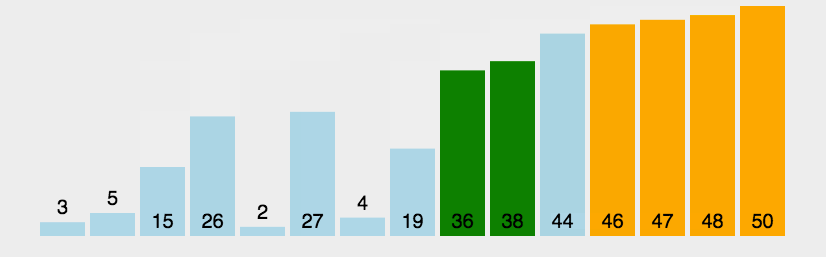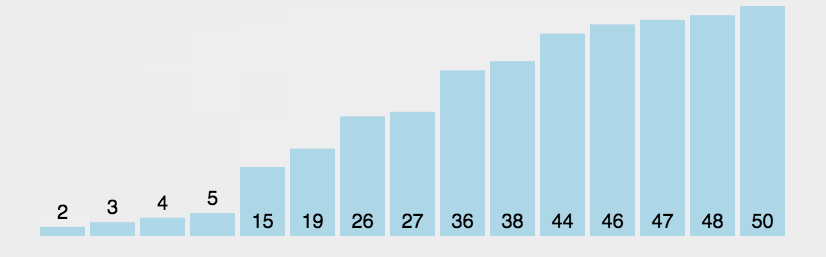
2.排序算法

void BubbleSort(int R[],int n) {
	int i, j;
	for (int i = 0; i < n - 1; i++) {
		for (int j = 0; j < n - 1 - i; j++) {//一次冒泡后，最大的元素已经在最右边
			if (R[j] > R[j + 1]) {
				swap(R[j],R[j+1]);//交换两个元素
			}
		}
	}
}
int main() {
	int R[] = { 4,5,6,3,2,1 };
	BubbleSort(R, 6);
	for (int i = 0; i < 6; i++) {
		printf("%d ", R[i]);
	}
	return 0;
}

3.算法分析

时间复杂度：最好$O(n)$,最坏$O(n^2)$,平均$O(n^2)$
空间复杂度：$O(1)$
稳定性：稳定

2.快速排序

1.排序思路

快速排序是由冒泡排序改进而得的，它的基本思想是在待排序的$n$个元素中任取一个元素（通常取第一个元素）作为基准，把该元素放入适当的位置后，数据序列被此元素划分为两部分。所有元素值小于基本元素值的放置在前一部分，所有值大于基准元素值的放置在后一部分，并把该元素排在这两部分的中间（称之为元素归位），这个过程称为一趟快速排序，即一趟划分；
之后对产生的两个部分分别重复上述过程，直至每部分内只有一个元素或位空为止。
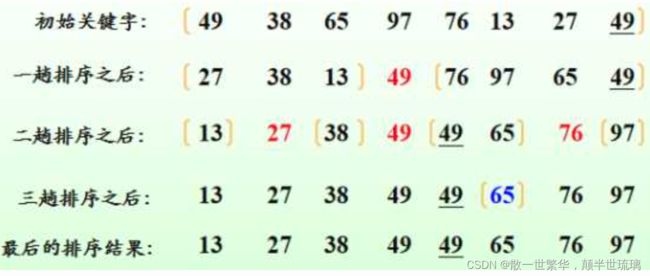
具体过程如下图所示：对数组[49,38,65,97,76,13,27,49]进行快速排序

为了方便加深读者的理解，这里配上GIF动态演示

2.排序算法

int partition(int R[], int s, int t) {//一趟划分
	int i = s;
	int j = t;
	int temp = R[i];
	while (i < j) {
		while (j > i && R[j] >= temp)
			j--;//从右往左扫描 找到一个小于temp的R[j]
		R[i] = R[j];
		while (i < j && R[i] <= temp)
			i++;//从左往右扫描 找到一个大于temp的R[i]
		R[j] = R[i];
	}
	R[i] = temp;
	return i;
}
void QuickSort(int R[],int s,int t) {
	int i;
	if (s < t) {
		i = partition(R, s, t);
		QuickSort(R, s, i - 1);//对左区间进行排序
		QuickSort(R, i + 1, t);//对右区间进行排序
	}
}

int main() {
	int R[] = { 4,5,6,3,2,1 };
	QuickSort(R,0,5);
	for (int i = 0; i < 6; i++) {
		printf("%d ", R[i]);
	}
	return 0;
}

3.算法分析

时间复杂度：平均$O(nlo{g}_{2}n)$ 最好$O(nlo{g}_{2}n)$ 最坏$O(n^2)$
空间复杂度：$O(lo{g}_{2}n)$
稳定性：不稳定
复杂性：较复杂