【数据结构】手撕红黑树
目录
一、红黑树简介
1、红黑树的简介
2、红黑树的性质
二、红黑树的插入(看叔叔的颜色就行)
1、为什么新插入的节点必须给红色?
2、插入红色节点后,判定红黑树性质是否被破坏
2.1情况一:uncle存在且为红
2.2情况二:uncle不存在/存在且为黑(直线)
2.3情况三:uncle不存在/存在且为黑(折线)
2.4总结
3、红黑树插入代码
三、红黑树的平衡检测
四、红黑树整体代码
一、红黑树简介
1、红黑树的简介
红黑树和AVL树一样,因其逻辑复杂,面试时现场要求手撕就是纯纯刁难面试者。但某大厂面试官曾要求某些求职者现场手撕红黑树(我赌5毛,让面试官撕,他也撕不出来,而且你家员工上班手搓红黑树啊?),随后求职遭遇被发到网上吐槽,这便有了“手撕红黑树”的梗,也让红黑树成为了知名度最高的数据结构。(话虽如此,对于红黑树的性质、插入思想等概念还是需要掌握的)
2、红黑树的性质
红黑树本质也是一种二叉搜索树。底层结构需要使用二叉搜索树的地方,基本上都会使用红黑树来实现,而AVL树也因此坐上了冷板凳。
红黑树通过在每个节点上添加一个存储位,用于存储“RED”或“BLACK”。通过节点上红/黑颜色限制,确保最长路径不超过最短路径的两倍,因而它是接近平衡的树形结构。最短路径:全黑;最长路径:一黑一红交替。
1、红黑树的根节点是黑色的;
2、没有连续的红色节点(如果某个节点为红色,则它的左右孩子必须是黑色)
3、无论哪个节点,其每条路径的黑色节点数量相同;
4、所有的空节点(NIL节点)可以认为是黑色的。
最优情况:全黑或每条路径都是一黑一红的满二叉树,高度logN
最差情况:每颗子树左子树全黑,右子树一黑一红。高度2*logN。
可以发现,最坏情况的时间复杂度和AVL树一样,都是O(logN),但是红黑树这种近似平衡的结构减少了大量旋转,综合性能优于AVL树。
二、红黑树的插入(看叔叔的颜色就行)
1、为什么新插入的节点必须给红色?
新节点给红色,可能会违反上面说的红黑树性质2;如果新节点给黑色,必定会违反性质3。
2、插入红色节点后,判定红黑树性质是否被破坏
情况一调整后可能变成情况一、情况二、情况三。
2.1情况一:uncle存在且为红
这种情况cur、parent、grandfather都是确定颜色的,唯独uncle的颜色是不确定的。
可以这么想:cur为红那么就需要将parent变为黑;parent变黑需要控制每条路径上黑节点的数量相同,那么就要把uncle变黑;如果grandfather不是根,需要反转为红,用以控制路径黑节点数量相同。继续向上调整即可。
2.2情况二:uncle不存在/存在且为黑(直线)
uncle的情况分两种。
uncle不存在,则cur为插入节点,单旋即可。
uncle存在且为黑是第一种情况变过来的。
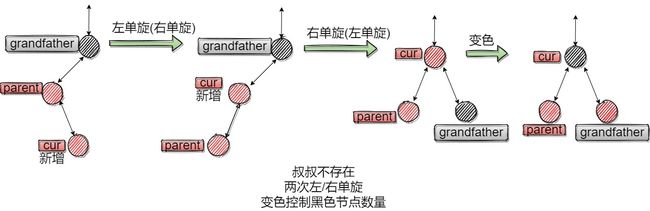
2.3情况三:uncle不存在/存在且为黑(折线)
uncle的情况分两种。
uncle不存在,则cur为插入节点,两次单旋即可。
uncle存在且为黑,先掰直
2.4总结
插入新节点时,父节点为红,看叔叔的颜色。
1、叔叔存在且为红,变色,向上调整(可能变为三种情况中的任意一种)
2、叔叔不存在/存在且为黑,直线。单旋+变色
3、叔叔不存在/存在且为黑,折线,两次单旋+变色
3、红黑树插入代码
bool Insert(const pair& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
_root->_col = BLACK;//根节点给黑色
return true;
}
//_root不为空
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else//相等说明元素相同,插入失败
return false;
}
//开始插入
cur = new Node(kv);
cur->_col = RED;//新插入节点给红色,可能违反规则。如果给黑色会导致其他路径的黑色节点数量不相同,必定违反规则。
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
cur->_parent = parent;//维护cur的父指针
}
else
{
parent->_left = cur;
cur->_parent = parent;
}
//调整
while (parent&&parent->_col == RED)
{
Node* grandfather = parent->_parent;//找到祖父
if (grandfather->_left == parent)//如果父亲是祖父的左孩子
{
Node* uncle = grandfather->_right;//找到叔叔
//情况一:叔叔存在且为红
if (uncle != nullptr && uncle->_col == RED)
{
//变色
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;
}
else//情况二或情况三
{
if (cur == parent->_left)//情况二,直线
{
RotateRight(grandfather);//右单旋
parent->_col = BLACK;
grandfather->_col = RED;
}
else//情况三,折线
{
RotateLeft(parent);//左单旋
RotateRight(grandfather);//右单旋
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
else//如果父亲是祖父的右孩子
{
Node* uncle = grandfather->_left;
if (uncle != nullptr && uncle->_col == RED)
{
parent->_col =uncle->_col= BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;
}
else
{
if (cur == parent->_right)//情况二,直线
{
//g
// p
// c
RotateLeft(grandfather);//左单旋
parent->_col = BLACK;
grandfather->_col = RED;
}
else//情况三,折线
{
//g
// p
//c
RotateRight(parent);//右单旋
RotateLeft(grandfather);//左单旋
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
}
_root->_col=BLACK;
return true;
} 三、红黑树的平衡检测
bool Check(Node* root,int blackNum,const int ref)//检查有没有连续红节点
{
if (root == nullptr)
{
if (blackNum != ref)
{
cout << "路径上黑节点数量不一致" << endl;
return false;
}
return true;
}
if (root->_col == BLACK)
{
++blackNum;
}
if (root->_col == RED && root->_parent->_col == RED)
{
cout << "违反规则,父子均为红" << endl;
return false;
}
return Check(root->_left, blackNum,ref) && Check(root->_right, blackNum, ref);
}
bool _IsBalance()
{
if (_root == nullptr)
return true;
if (_root->_col != BLACK)
{
return false;
}
//数一下一条路径黑色节点数量
int ref = 0;//统计一条路上黑色节点的数量
Node* left = _root;
while (left != nullptr)
{
if (left->_col == BLACK)
{
++ref;
}
left = left->_left;
}
return Check(_root,0,ref);
}1、在_IsBalance中确定号一条路径中黑色节点的数量,作为参数传递给Check函数,Check函数需要在递归至根节点时,统计,每条路径黑色节点数量是否和基准值ref相等。
2、Check函数中还需要判断:子节点为红,父节点也为红(此时不平衡)
四、红黑树整体代码
#pragma once
#include
#include