图像频域及滤波处理
图像频域及滤波处理
我们尝试使用一下频域图像,也主要是傅里叶(FFT),图像如下:
频率及FFT:
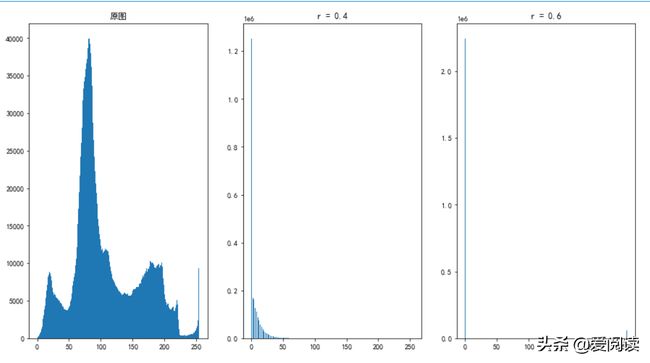
首先,将空间域图像转换为时间域,看一下分布情况:
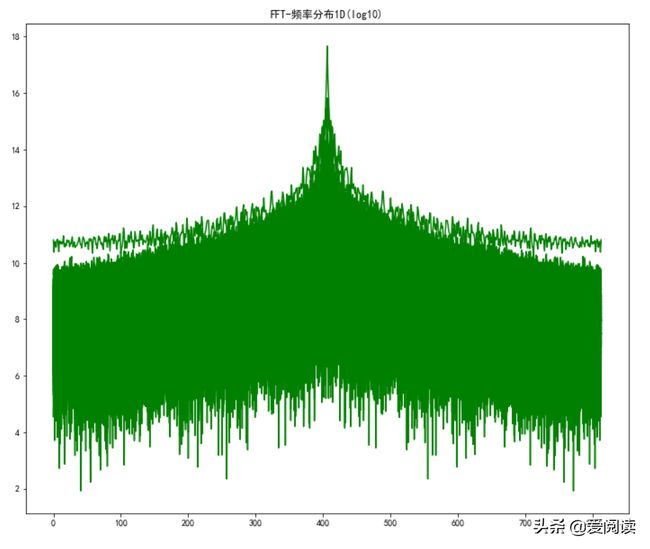
我们再看看一维频率分布情况:
h, w = gray.shape
x=np.arange(h)
plt.figure(figsize=(12,10))
plt.plot(x, log_p, 'g'), plt.title("FFT-频率分布1D(log10)")
plt.show()通过观察上图,中心的低频区域大概100左右,我们可以通过高频滤波器保留高频部分,结果如下:
dft = cv2.dft(gray2.astype('float32'), flags = cv2.DFT_COMPLEX_OUTPUT) ### FFT
dft_shift = np.fft.fftshift(dft)
magnitude_spectrum = 20*np.log(cv2.magnitude(dft_shift[:,:,0],dft_shift[:,:,1])) # 幅值对数变换
## 高频增强处理
D = 50
crow = dft_shift.shape[0]//2
ccol = dft_shift.shape[1]//2
dft_shift[crow-D:crow+D, ccol-D:ccol+D] = 0
dft_ishift = np.fft.ifftshift(dft_shift)
img_ = cv2.idft(dft_ishift)
img_back1 = cv2.magnitude (img_[:,:,0],img_[:,:,1])
img_back1a = np.zeros(gray2.shape, np.uint8)
img_back1a = (255.0 * img_back1/np.max(img_back1) ).astype(np.uint8)
img_back1a_hist = 4.0*img_back1a + 50
img_back1a_hist = np.round(img_back1a_hist)
img_back1a_hist = img_back1a_hist.astype(np.uint8)
效果如下:
高频滤波结果
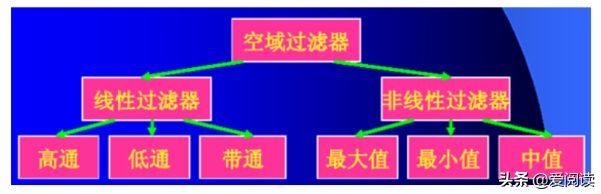
滤波及分类:
滤波作用:高通滤波用于边缘检测,低通滤波用于图像平滑去噪;
(1)方波:线性滤波
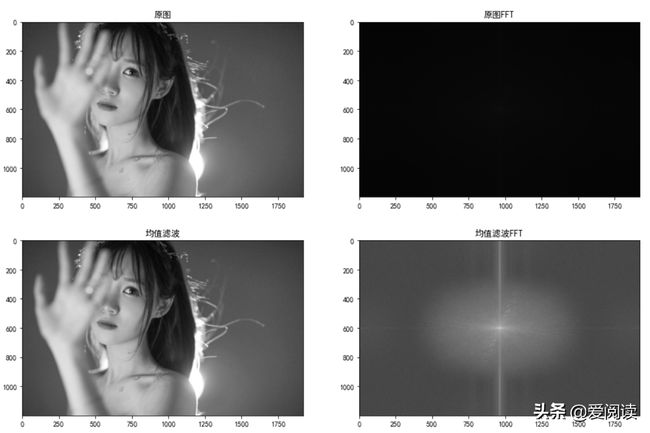
(2)均值滤波:线性滤波
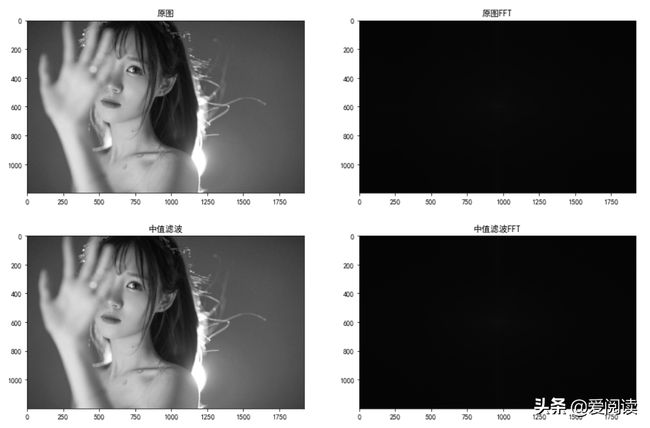
(3)中值滤波:(非线性滤波)
(4)高斯滤波:线性滤波
r = cv2.GaussianBlur(gray2, (3,3), 7)
f1 = gray_f_spectrum(gray2)
f2 = gray_f_spectrum(r)
plt.figure(figsize=(15, 10))
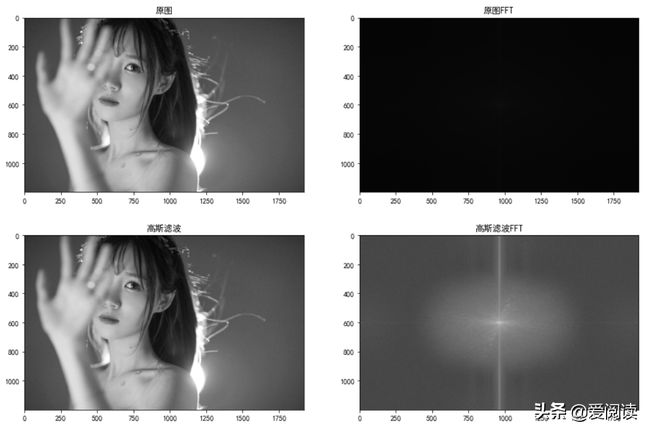
plt.subplot(221), plt.imshow(gray2, 'gray'), plt.title("原图")
plt.subplot(222), plt.imshow(f1, 'gray'), plt.title("原图FFT")
plt.subplot(223), plt.imshow(r, 'gray'), plt.title("高斯滤波")
plt.subplot(224), plt.imshow(f2, 'gray'), plt.title("高斯滤波FFT")
拉普拉斯卷积核
kernLaplace = np.array([[0, 1, 0], [1, -4, 1], [0, 1, 0]]) # Laplacian kernel
Laplace1 = cv2.filter2D(gray2, -1, kernLaplace, borderType=cv2.BORDER_REFLECT)
# 使用 cv2.Laplacian 实现 Laplace 卷积算子
Laplace2 = cv2.Laplacian(gray2, -1, ksize=3)
imgRecovery = cv2.add(gray2, Laplace2) # 恢复原图像
# 二值化边缘图再卷积
_, binary = cv2.threshold(gray2, 0, 255, cv2.THRESH_BINARY | cv2.THRESH_TRIANGLE)
Laplace3 = cv2.Laplacian(binary, cv2.CV_64F)
Laplace3 = cv2.convertScaleAbs(Laplace3)
plt.figure(figsize=(15, 10))
plt.subplot(131), plt.axis('off'), plt.title("原图")
plt.imshow(gray2, 'gray', vmin=0, vmax=255)
plt.subplot(132), plt.axis('off'), plt.title("cv2.Laplacian:拉普拉斯")
plt.imshow(Laplace2, 'gray', vmin=0, vmax=255)
plt.subplot(133), plt.axis('off'), plt.title("thresh-Laplacian")
plt.imshow(Laplace3, 'gray', vmin=0, vmax=255)
plt.tight_layout()
plt.show()
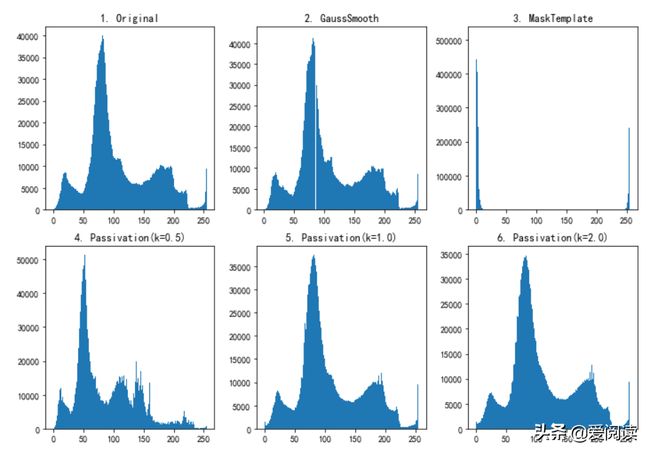
钝化掩蔽
今天就分享到这里, 我是paperClub。
备注:WeiXin 搜索paperClub, 添加关注并回复【paperClub】即可获取使用方法。
1. 感谢各位小伙伴的关注, 您的点赞、鼓励和留言,都是我深夜坚持的一份动力,无论褒贬,都是我们行进途中最好的回馈,也都会被认真对待。
2. 我将持续分享各类、好玩且有趣的算法应用及工程和项目,欢迎分享和转发。沟通、学习和交流,请与我联系,虽然平时忙,但留言必回,勿急,感谢理解!
3. 分享内容包括开源项目和自研项目,如在引用或使用时,考虑不周、遗漏引用信息或涉及版权等,请您及时联系。如果您对某些内容感兴趣,我们可以一起讨论、交流和学习。