Python数据结构与算法篇（十三）-- 位运算与使用技巧

        计算机中的数在内存中都是以二进制形式进行存储的，用位运算就是直接对整数在内存中的二进制位进行操作，因此其执行效率非常高，在程序中尽量使用位运算进行操作，这会大大提高程序的性能。

1 操作符

1.1 基本运算

• & 与运算 两个位都是 1 时，结果才为 1，否则为 0，如

    1 0 0 1 1 
 &  1 1 0 0 1 
 ------------------------------   
    1 0 0 0 1 

• | 或运算 两个位都是 0 时，结果才为 0，否则为 1，如

    1 0 0 1 1 
|   1 1 0 0 1 
------------------------------   
    1 1 0 1 1 

• ^ 异或运算，两个位相同则为 0，不同则为 1，如

    1 0 0 1 1 
^   1 1 0 0 1 
-----------------------------   
    0 1 0 1 0 

• ~ 取反运算，0 则变为 1，1 则变为 0，如

~  1 0 0 1 1 
-----------------------------   
   0 1 1 0 0 ​

1.2 左移操作<< 与 右移操作>>

左移操作
        左移操作，左移一位相当于乘以 b，a<

print(2<<3)     # 2*2^3 = 16，2的二进制10，向左移动3位后10000
print(2<<1)     # 2*2^1 = 4
print(3<<4)     # 3*2^4 = 48,3的二进制为11，向左移动四位后110000

右移操作
        右移操作，右移一位相当于除以 b，a>>b, a' = a//(2^b)注意这里是整除，当向右移动位数大于能移动的位数时，置为0【可以理解为会将尾巴截掉】

print(2>>3)     # 2//2^3 = 0，2的二进制10，向右最多移动2位后，所以多移动无疑为 0
print(2>>1)     # 2//2^1 = 1，向右移动一位为 01,
print(3>>4)     # 3//2^4 = 0, 3 的二进制为11，向右移动四位后00
print(3>>1)     # 3//2^1 = 1, 3 的二进制为11，向右移动一位后为01

$>>$ 和 $<<$ 都是位运算，对二进制数进行移位操作。$<<$ 是左移，末位补 0，类比十进制数在末尾添 0 相当于原数乘以 10，$x<<1$ 是将 $x$ 的二进制表示左移一位，相当于原数 $x$ 乘 2。比如整数 4 在二进制下是100，$4<<1$ 左移1位变成1000(二进制)，结果是 8。$>>$ 是右移，右移1位相当于除以2。


而 $>>=$ 和 $<<=$，就是对变量进行位运算移位之后的结果再赋值给原来的变量，可以类比赋值运算符 $+=$ 和 $-=$ 可以理解。比如 $x>>=2$， 就是把变量 $x$ 右移2位，再保留x操作后的值。

2 常见位运算问题

2.1 位操作实现乘除法

        数 a 向右移一位，相当于将 a 除以 2；数 a 向左移一位，相当于将 a 乘以 2

a = 2
a >> 1  # 1
a << 1  # 4

2.2 位操作交换两数

        位操作交换两数可以不需要第三个临时变量，虽然普通操作也可以做到，但是没有其效率高

a, b = b, a         # 普通操作

# 位操作
a ^= b
b ^= a
a ^= b

解释

• 第一步：a ^= b —> a = (a^b)
• 第二步：b ^= a —> b = b^(ab) —> b = (b^b)a = a
• 第三步：a ^= b —> a = (a^b)a = (a^a)b = b

2.3 位操作判断奇偶数

        要根据数的最后一位是 0 还是 1 来决定即可，为 0 就是偶数，为 1 就是奇数。

if a & 1 == 0:
    print("偶数")

2.4 位操作交换符号

        交换符号将正数变成负数，负数变成正数

def reversal(a):
    return ~a + 1

        正数取反加1，正好变成其对应的负数(补码表示)；负数取反加一，则变为其原码，即正数

2.5 位操作求绝对值

        正数的绝对值是其本身，负数的绝对值正好可以对其进行取反加一求得，即我们首先判断其符号位（整数右移 31 位得到 0，负数右移 31 位得到 -1，即 0xffffffff），然后根据符号进行相应的操作

def abs(a):
    i = a >> 31
    return a if i == 0 else (~a+1)

        上面的操作可以进行优化，可以将 i == 0 的条件判断语句去掉。我们都知道符号位 i 只有两种情况，即 i = 0 为正，i = -1 为负。对于任何数与 0 异或都会保持不变，与 -1 即 0xffffffff 进行异或就相当于对此数进行取反，因此可以将上面三目元算符转换为 ((a^i)-i)，即整数时 a 与 0 异或得到本身，再减去 0，负数时与 0xffffffff 异或将 a 进行取反，然后在加上 1，即减去 i(i =-1)

def abs2(a):
     i = a >> 31
     return ((a^i)-i)

2.6 位操作进行高低位交换

        给定一个 16 位的无符号整数，将其高 8 位与低 8 位进行交换，求出交换后的值，如：

34520的二进制表示：
10000110 11011000

将其高8位与低8位进行交换，得到一个新的二进制数：
11011000 10000110
其十进制为55430

        从上面移位操作我们可以知道，只要将无符号数 a >> 8 即可得到其高 8 位移到低 8 位，高位补 0；将 a << 8 即可将 低 8 位移到高 8 位，低 8 位补 0，然后将 a >> 8 和 a << 8 进行或操作既可求得交换后的结果。

a = 34520
a = (a >> 8) | (a << 8)

2.7 位操作进行二进制逆序

        将无符号数的二进制表示进行逆序，求取逆序后的结果，如

数34520的二进制表示：
10000110 11011000

逆序后则为：
00011011 01100001
它的十进制为7009

        在字符串逆序过程中，可以从字符串的首尾开始，依次交换两端的数据。在二进制中使用位的高低位交换会更方便进行处理，这里我们分组进行多步处理。

• 第一步：以每 2 位为一组，组内进行高低位交换

交换前： 10 00 01 10 11 01 10 00
交换后： 01 00 10 01 11 10 01 00

• 第二步：在上面的基础上，以每 4 位为 1 组，组内高低位进行交换

交换前： 0100 1001 1110 0100
交换后： 0001 0110 1011 0001

• 第三步：以每 8 位为一组，组内高低位进行交换

交换前： 00010110 10110001
交换后： 01100001 00011011

• 第四步：以每16位为一组，组内高低位进行交换

交换前： 0110000100011011
交换后： 0001101101100001

        对于上面的第一步，依次以 2 位作为一组，再进行组内高低位交换，这样处理起来比较繁琐，下面介绍另外一种方法进行处理。先分别取原数 10000110 11011000 的奇数位和偶数位，将空余位用 0 填充：

原数：  10000110 11011000
奇数位： 10000010 10001000
偶数位： 00000100 01010000

        再将奇数位右移一位，偶数位左移一位，此时将两个数据相或即可以达到奇偶位上数据交换的效果：

原数：  10000110 11011000
奇数位右移一位： 0 10000010 1000100
偶数位左移一位：0000100 01010000 0
两数相或得到： 01001001 11100100

        上面的方法用位操作可以表示为：

• 取 a 的奇数位并用 0 进行填充可以表示为：a & 0xAAAA
• 取 a 的偶数为并用 0 进行填充可以表示为：a & 0x5555 因此，上面的第一步可以表示为：
  a = ((a & 0xAAAA) >> 1) | ((a & 0x5555) << 1)

        同理，可以得到其第二、三和四步为：

• a = ((a & 0xCCCC) >> 2) | ((a & 0x3333) << 2)
• a = ((a & 0xF0F0) >> 4) | ((a & 0x0F0F) << 4)
• a = ((a & 0xFF00) >> 8) | ((a & 0x00FF) << 8)

        因此整个操作为：

a = 34520;
a = ((a & 0xAAAA) >> 1) | ((a & 0x5555) << 1)
a = ((a & 0xCCCC) >> 2) | ((a & 0x3333) << 2)
a = ((a & 0xF0F0) >> 4) | ((a & 0x0F0F) << 4)
a = ((a & 0xFF00) >> 8) | ((a & 0x00FF) << 8)

2.8 位操作统计二进制中 1 的个数

        统计二进制1的个数可以分别获取每个二进制位数，然后再统计其1的个数，此方法效率比较低。这里介绍另外一种高效的方法，同样以 34520 为例，我们计算其 a &= (a-1)的结果：

• 第一次：计算前：1000 0110 1101 1000 计算后：1000 0110 1101 0000
• 第二次：计算前：1000 0110 1101 0000 计算后：1000 0110 1100 0000
• 第三次：计算前：1000 0110 1100 0000 计算后：1000 0110 1000 0000

        我们发现，没计算一次二进制中就少了一个 1，则我们可以通过下面方法去统计：

count = 0
while(a):
    a = a & (a-1)
    count += 1

2.9 原码、反码、补码

        机器数：一个数在计算机中的二进制表示形式，机器数带符号，在计算机用一个数的最高位存放符号，正数为0，负数为1

        例如： 十进制中的数 +3 ，计算机字长为8位，转换成二进制就是00000011。如果是 -3 ，就是 10000011。其中，00000011 和 10000011就是机器数

        真值：将带符号位的机器数对应的真正数值称为机器数的真值。

1. 原码

        原码就是符号位加上真值的绝对值，即用第一位表示符号, 其余位表示值。例如：如果是8位二进制，那么

[+1]原 = 0000 0001
[-1]原 = 1000 0001

        第一位是符号位. 因为第一位是符号位, 所以8位二进制数的取值范围就是:

[1111 1111, 0111 1111]
[-127, 127]

        原码在展示上是与机器数相同的

2. 反码

        反码的表示方法是:

• 正数的反码是其本身
• 负数的反码是在其原码的基础上, 符号位不变，其余各个位取反。

[+1] = [00000001]原 = [00000001]反
[-1] = [10000001]原 = [11111110]反

3. 补码

        补码的表示方法是:

• 正数的补码就是其本身
• 负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1。(即在反码的基础上+1)

[+1] = [00000001]原 = [00000001]反 = [00000001]补
[-1] = [10000001]原 = [11111110]反 = [11111111]补

        对于负数, 补码表示方式也是人脑无法直观看出其数值的。通常也需要转换成原码在计算其数值。不管 n 是正数还是负数，只需要下面的语句便可得到此数的补码：

bin(n & 0xffffffff)

        了解更多，请移步：原码反码补码的通俗解释

2.10 进制之间的转换

        二进制、八进制、十进制、十六进制转换：

print(bin(10))          # '0b1010'
print(bin(-10))         # '-0b1010'
print(oct(10))          # '0o12'
print(hex(10))          # '0xa'
a = 0b1010
b = 0x11
x = '1010'
y = '11'
print(a)                # 10
print(int(x, 2))        # 10
print(b)                # 17
print(int(y, 16))       # 17

3 常见题型

3.1 题库列表

190. 颠倒二进制位	191. 位1的个数	461. 汉明距离
268. 丢失的数字	136. 只出现一次的数字	137. 只出现一次的数字 II
260. 只出现一次的数字 III	231. 2 的幂	338. 比特位计数
371. 两整数之和	405. 数字转换为十六进制数	476. 数字的补数
477. 汉明距离总和	526. 优美的排列	1178. 猜字谜

3.2 真题演练

190. 颠倒二进制位

class Solution:
    def reverseBits(self, n: int) -> int:
        '''
        res = 0
        for _ in range(32):
            res = (res << 1) | (n & 1)
            n >>= 1
        return res
        '''
        n = (n >> 16) | (n << 16)
        n = ((n & 0xff00ff00) >> 8) | ((n & 0x00ff00ff) << 8)
        n = ((n & 0xf0f0f0f0) >> 4) | ((n & 0x0f0f0f0f) << 4)
        n = ((n & 0xcccccccc) >> 2) | ((n & 0x33333333) << 2)
        n = ((n & 0xaaaaaaaa) >> 1) | ((n & 0x55555555) << 1)
        return n

191. 位1的个数
        题目描述：编写一个函数，输入是一个无符号整数（以二进制串的形式），返回其二进制表达式中数字位数为 ‘1’ 的个数（也被称为汉明重量）。

1. 消除二进制末尾的 1

class Solution:
    def hammingWeight(self, n: int) -> int:
        count = 0
        while n:
            n &= (n-1)
            count += 1
        return count

2. 右移 32 次

class Solution:
    def hammingWeight(self, n: int) -> int:
        count = 0
        for _ in range(32):
            count += n & 1
            n >>= 1
        return count

3. 库函数

class Solution:
    def hammingWeight(self, n: int) -> int:
        return bin(n).count('1')

461. 汉明距离

        题目描述：两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。给你两个整数 x 和 y，计算并返回它们之间的汉明距离。

1. 异或速解

class Solution:
    def hammingDistance(self, x: int, y: int) -> int:
        return bin(x^y).count('1')

2. 统计1的个数

class Solution:
    def hammingDistance(self, x: int, y: int) -> int:
        z = x ^ y           # 异或运算，二进制位不同的位置为1
        count = 0
        while z:            # 统计运算之后结果中 1 的个数
            z = z & (z-1)   
            count += 1
        return count

3. 字符串解题

class Solution:
    def hammingDistance(self, x, y):
        count = 0
        bx, by = bin(x)[2:].zfill(32), bin(y)[2:].zfill(32)
        for i in range(32):
            if bx[i] != by[i]:
                count += 1
        return count

268. 丢失的数字

        题目描述：给定一个包含 [0, n] 中 n 个数的数组 nums ，找出 [0, n] 这个范围内没有出现在数组中的那个数。

        思路分析：以示例 1 为例 nums = [3,0,1]，其长度为3，不难看出其不缺失的原数组为 [0, 1, 2, 3]。如果将nums与其原数组异或会发生什么呢？异或满足交互律 即 (a^b)c = a^(bc)。我们不妨将其调整一下位置，即
nums 原数组

 0   ^    0     => 0
 1   ^    1     => 0
 无 2 => 2
 3   ^    3     => 0

        所有一样的数全部异或之后成了0，最后所剩下的2与0异或即为本身，也就是所缺失的数。

class Solution:
    def missingNumber(self, nums: List[int]) -> int:
        ans = 0
        for i, num in enumerate(nums):  # 此处 num 代表nums， i 代表原数组
            ans ^= i ^ num
        return ans ^ len(nums)          # 因为原数组比nums长度多1, 所有这里多异或了一次

136. 只出现一次的数字

        题目描述：给你一个 非空 整数数组 nums ，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。你必须设计并实现线性时间复杂度的算法来解决此问题，且该算法只使用常量额外空间。

        对于这道题，可使用异或运算 ⊕。异或运算有以下三个性质。

• 任何数和 0 做异或运算，结果仍然是原来的数，即 $a\oplus 0=a$。
• 任何数和其自身做异或运算，结果是 0，即 $a\oplus a=0$。
• 异或运算满足交换律和结合律，即 $a\oplus b\oplus a=b\oplus a\oplus a=b\oplus (a\oplus a)=b\oplus 0=b$。

class Solution:
    def singleNumber(self, nums: List[int]) -> int:
        '''异或运算'''
        re = 0
        for num in nums:
            re ^= num
        return re

137. 只出现一次的数字 II

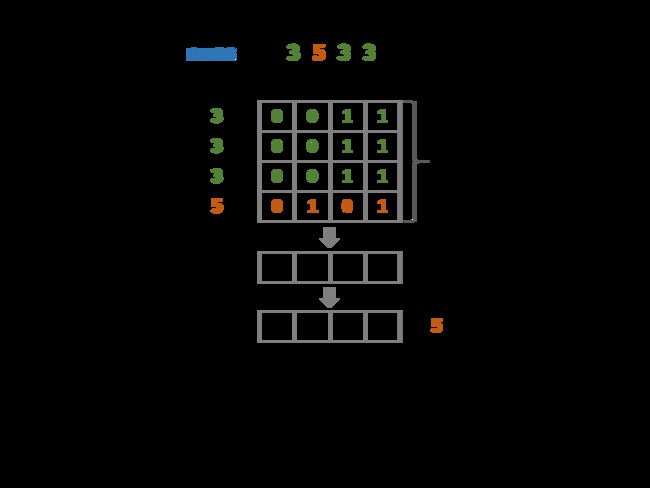
        题目描述：给你一个整数数组 nums，除某个元素仅出现 一次 外，其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。

class Solution:
    def singleNumber(self, nums: List[int]) -> int:’
        '''
        # 数学运算
        return (sum(set(nums))*3-sum(nums)) // 2
        '''
        ans = 0
        for i in range(32):             # nums[i] 是32位整数，
            sum = 0                     # 针对每一位的对应二进制数值求和
            for num in nums:
                sum += (num >> i) & 1   # 提取从右往左数第i位的数值，将所有nums[i], 二进制下的第i位数值进行求和
            if sum % 3 == 1:            # 如果没办法被3整除，那么说明落单的那个数的第i位是 1 不是 0
                ans |= 1 << i           # 恢复第 i 位的值到 ans
        return ~(ans^0xffffffff) if sum % 3 == 1 else ans   # 这里最后的sum是符号位，可以判断最后输出的数字是否是负数

        温馨提示： 由于 Python 的存储负数的特殊性，需要先将 0-32 位取反（即 res^0xffffffff ），再将所有位取反（即 ~ ）。两个组合操作实质上是将数字 32 以上位取反，0-32位不变。

260. 只出现一次的数字 III

        题目描述：给你一个整数数组 nums，其中恰好有两个元素只出现一次，其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。你必须设计并实现线性时间复杂度的算法且仅使用常量额外空间来解决此问题。

class Solution:
    def singleNumber(self, nums: List[int]) -> List[int]:
        mask = 0
        for num in nums:            # 异或运算，目的是找到两个落单数值的不同，便于后面分类
            mask ^= num
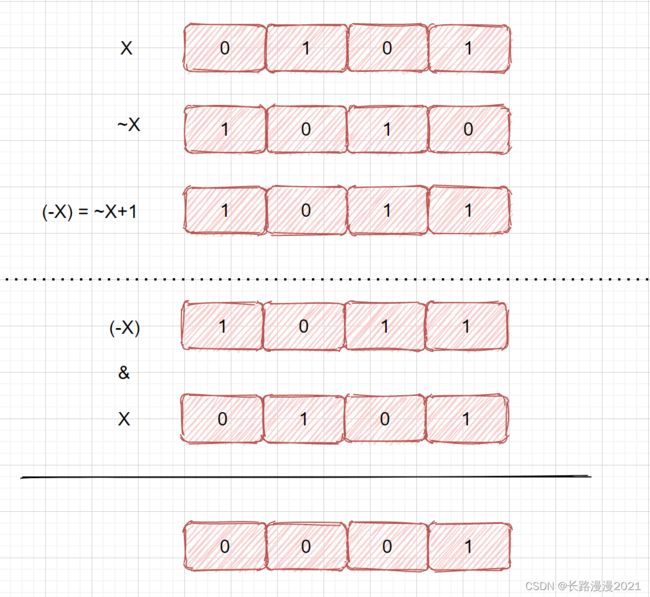
        mask  &= (-mask)            # 直接获取 mask 二进制表示的最低位的 1
        type1, type2 = 0, 0         
        for num in nums:            # 把数组分为两部分，每部分再分别异或
            if mask & num:          # 对于 num，如果 mask 为1，分类为 type1，对这个 type1 进行异或，可以找到落单的数值
                type1 ^= num
            else:                   # 如果 num 的 mask 对应的是0，那么异或找到另一个落单的数值
                type2 ^= num
        return [type1, type2] 

231. 2 的幂
        题目描述：给你一个整数 n，请你判断该整数是否是 2 的幂次方。如果是，返回 true；否则，返回 false。如果存在一个整数 x 使得 $n==2^x$ ，则认为 n 是 2 的幂次方。

class Solution:
    def isPowerOfTwo(self, n: int) -> bool:
        # return n>0 and n&(-n)==n   
        return n>0 and n&(n-1)==0   

338. 比特位计数

        题目描述：给你一个整数 $n$ ，对于 $0<=i<=n$ 中的每个 $i$ ，计算其二进制表示中 1 的个数 ，返回一个长度为 $n+1$ 的数组 ans 作为答案。

        思路分析：对于正整数 $x$，将其二进制表示右移一位，等价于将其二进制表示的最低位去掉，得到的数是 $\lfloor \frac{x}{2}\rfloor$。如果 $bits[\lfloor \frac{x}{2}\rfloor ]$ 的值已知，则可以得到 $bits[x]$ 的值：

• 如果 $x$ 是偶数，则 $bits[x]=bits[\lfloor \frac{x}{2}\rfloor ]$；
• 如果 $x$ 是奇数，则 $bits[x]=bits[\lfloor \frac{x}{2}\rfloor ]+1$。

        上述两种情况可以合并成: $bits[x]$ 的值等于 $bits[\lfloor \frac{x}{2}\rfloor ]$ 的值加上 $x$ 除以 2 的余数。由于$\lfloor \frac{x}{2}\rfloor$ 可以通过 $x>>1$ 得到，$x$ 除以 2 的余数可以通过 $x\&1$ 得到，因此有: $bits[x]=bits[x>>1]+(x\&1)$。

        另一种思路：令 $y=x\&(x—1)$，则 $y$ 为将 $x$ 的最低设置位从 1 变成 0 之后的数，显然 $0\le y<x$, $bits[x]=bits[y]＋+1$。因此对任意正整数 $x$，都有 $bits[x]=bits[x\&(x-1)]+1$。

class Solution:
    def countBits(self, n: int) -> List[int]:
        '''
        # 遍历与统计
        return [bin(i).count('1') for i in range(n+1)]
        '''
        # 动态规划
        ans = [0] * (n+1)
        for i in range(1, n+1):
            ans[i] = ans[i>>1] + (i&1)      # ans[i] = ans[i&(i-1)]+1
        return ans

342. 4的幂

        题目描述：给定一个整数，写一个函数来判断它是否是 4 的幂次方。如果是，返回 true；否则，返回 false。整数 n 是 4 的幂次方需满足：存在整数 x 使得 $n==4^x$

        思路分析：如果 n 是 4 的幂，那么 n 一定也是 2 的幂。因此我们可以首先判断 n 是否是 2 的幂，在此基础上再判断 n 是否是 4 的幂。如果 n 是 4 的幂，那么 n 的二进制表示中有且仅有一个 1，并且这个 1 出现在从低位开始的第偶数个二进制位上（这是因为这个 1 后面必须有偶数个0）。因此我们可以构造一个整数 mask，它的所有偶数二进制位都是 0，所有奇数二进制位都是 1。这样一来，我们将 n 和 mask 进行按位与运算，如果结果为 0，说明 n 二进制表示中的 1 出现在偶数的位置，否则说明其出现在奇数的位置。

        思路二：如果 n 是 4 的幂，可以发现它除以 3 的余数一定为 1

class Solution:
    def isPowerOfFour(self, n: int) -> bool:
        # return n > 0 and n&(n-1) == 0 and (n%3) == 1
        return n > 0 and n&(n-1) == 0 and (n&0xaaaaaaaa) == 0

371. 两整数之和

        题目描述：给你两个整数 a 和 b ，不使用 运算符 + 和 - ​​​​​​​，计算并返回两整数之和。

class Solution:
    def getSum(self, a: int, b: int) -> int:
        mask1 = 0xffffffff
        a &= mask1
        b &= mask1
        while b:
            carry = (a & b) << 1        # 将存在进位的位置置1
            a ^= b                      # 计算无进位的结果
            b = carry
        return a if a < 0x80000000 else ~(a^mask1)  # 考虑负数时的输出
# @lc code=end

405. 数字转换为十六进制数

        题目描述：给定一个整数，编写一个算法将这个数转换为十六进制数。对于负整数，我们通常使用 补码运算 方法。

1. 精简版

class Solution:
    def toHex(self, num: int) -> str:
        # return hex(num&0xffffffff)[2:]       
        '''模拟法'''
        CONV = '0123456789abcdef'
        ans = ''
        if num == 0:
            return '0'
        elif num < 0:
            num = 2 ** 32 + num             
        while num > 0:
            num, res = divmod(num, 16)
            ans += CONV[res]
        
        return ans[::-1]

2. 详细版

class Solution:
    def toHex(self, num: int) -> str:
        CONV = "0123456789abcdef"
        ans = []    
        # 32位2进制数，转换成16进制 -> 4个一组，一共八组
        for _ in range(8):
            # 当输入值num为-1 ，第一次进入循环
            ans.append(num % 16)    # num % 16 = 15
            num //= 16              # num // 16 = -1
            # Python中的//运算取整除：向下取接近商的整数
            # % 取模运算返回整除的余数 （余数 = 被除数 - 除数 * 商）
            # 负整数 // 正整数 的最大值为-1
            # -1 // 16 = -1
            # -1 % 16 = 15
            # 即如num为负数，则一定会跑满for的8次循环
            # 正整数 // 正整数 的最小值为0
            # 1 // 16 = 0
            # 1 % 16 = 1
            # 即num为正数时，有可能触发下面的if语句，提前结束for循环
            if not num:     # 如果num不为0则继续下一次for循环
                break       # 如果num为0则终止for循环
            # 正整数 // 负整数 的最大值为-1，如1 // -16 = -1; 1 % -16 = -15
        return "".join(CONV[n] for n in ans[::-1])

476. 数字补数

        题目描述：对整数的二进制表示取反（0 变 1 ，1 变 0）后，再转换为十进制表示，可以得到这个整数的补数。例如，整数 5 的二进制表示是 “101”，取反后得到 “010”，再转回十进制表示得到补数 2。给你一个整数 num ，输出它的补数。

1. 与运算

class Solution:
    def findComplement(self, num: int) -> int:
        i, ans = 0, 0
        while num:
            if not (num & 1):           # 该位为0
                ans |= (1 << i)
            num >>= 1
            i += 1
        return ans

2. 异或运算

class Solution:
    def findComplement(self, num: int) -> int:
        num_copy = num
        num_1 = 1              
        while num_copy:
            num_1 <<= 1 
            num_copy >>= 1
        return num ^ (num_1-1)          # num_1 二进制位数比num多一位，减1后与num二进制位数相同，且各位均为1

3. 遍历字符串

class Solution:
    def findComplement(self, num: int) -> int:
        result = []
        for bt in bin(num)[2:]:
            if bt == '0':
                result.append('1')
            else:
                result.append('0')
        return int(''.join(result), 2)

477. 汉明距离的总和
        题目描述：两个整数的 汉明距离 指的是这两个数字的二进制数对应位不同的数量。给你一个整数数组 nums，请你计算并返回 nums 中任意两个数之间 汉明距离的总和 。

        对于某个 nums[i] 我们只关心在 nums 中有多少数的第 $x$ 位的与其不同，而不关心具体是哪些数与其不同，同时二进制表示中非 0 即 1。

        这样我们可以建立两个集合 $s_0$ 和 $s_1$，分别统计出 nums 中所有数的第 $x$ 位中 0 的个数和 1 的个数，集合中的每次计数代表了 nums 中的某一元素，根据所在集合的不同代表了其第 $x$ 位的值。那么要找到在 nums 中有多少数与某一个数的第 $x$ 位不同，只需要读取另外一个集合的元素个数即可，变成了 $O(1)$ 操作。那么要求得「第 $x$ 位所有不同数」的对数的个数，只需要应用乘法原理，将两者元素个数相乘即可。

class Solution:
    def totalHammingDistance(self, nums: List[int]) -> int:
        ans = 0
        for i in range(32):
            temp = sum((num >> i) & 1 for num in nums)
            ans += temp * (len(nums) - temp)
        return ans

526. 优美的排列

        题目描述：假设有从 1 到 n 的 n 个整数。用这些整数构造一个数组 perm（下标从 1 开始），只要满足下述条件 之一 ，该数组就是一个 优美的排列 ：

• perm[i] 能够被 i 整除
• i 能够被 perm[i] 整除

        给你一个整数 n ，返回可以构造的 优美排列 的 数量 。

class Solution:
    def countArrangement(self, n: int) -> int:
        canFill = defaultdict(list)
        for i in range(1,n+1):
            for j in range(1, n+1):
                if j % i == 0 or i % j == 0:        # 每个位置可以填入哪些数
                    canFill[i].append(j-1)

        order = sorted(canFill.keys(), key=lambda x:len(canFill[x]))    # 根据可填入数字的个数排序，优先填入个数少的
        end = (1 << n) - 1

        @lru_cache(None)
        def dfs(state):
            if state == end:                    # 全部填入
                return 1
            cnts = ans = 0
            for i in range(n):                  # 当前该填第几个位置
                if (1 << i) & state:
                    cnts += 1
            for i in canFill[order[cnts]]:      # 当前位置可以填哪些数
                if not ((1 << i) & state):      # 哪些数还没被填
                    ans += dfs(state ^ (1 << i))
            return ans
        
        return dfs(0)

1178. 猜字谜

题目描述

class Solution:
    def findNumOfValidWords(self, words: List[str], puzzles: List[str]) -> List[int]:
        frequency = collections.Counter()

        for word in words:
            mask = 0
            for ch in word:
                mask |= (1 << (ord(ch) - ord("a")))
            if str(bin(mask)).count("1") <= 7:
                frequency[mask] += 1
        
        ans = list()
        for puzzle in puzzles:
            total = 0

            # 枚举子集方法一
            # for choose in range(1 << 6):
            #     mask = 0
            #     for i in range(6):
            #         if choose & (1 << i):
            #             mask |= (1 << (ord(puzzle[i + 1]) - ord("a")))
            #     mask |= (1 << (ord(puzzle[0]) - ord("a")))
            #     if mask in frequency:
            #         total += frequency[mask]

            # 枚举子集方法二
            mask = 0
            for i in range(1, 7):
                mask |= (1 << (ord(puzzle[i]) - ord("a")))
            
            subset = mask
            while subset:
                s = subset | (1 << (ord(puzzle[0]) - ord("a")))
                if s in frequency:
                    total += frequency[s]
                subset = (subset - 1) & mask
            
            # 在枚举子集的过程中，要么会漏掉全集 mask，要么会漏掉空集
            # 这里会漏掉空集，因此需要额外判断空集
            if (1 << (ord(puzzle[0]) - ord("a"))) in frequency:
                total += frequency[1 << (ord(puzzle[0]) - ord("a"))]

            ans.append(total)
        
        return ans

---

位运算和使用技巧暂时告一段落，后面在学习中持续补充，谢谢大家的鼓励和支持！

---

参考

• Python位运算——左移操作（＜＜）右移操作＞＞：https://blog.csdn.net/qq_45769063/article/details/118618810
• Python异或运算：https://www.jianshu.com/p/ffa9fdf192a5
• 位运算技巧：https://www.zhihu.com/question/38206659
• 位运算：http://graphics.stanford.edu/~seander/bithacks.html#OperationCounting