常见算法实现



转自 ：http://blog.csdn.net/Xiongchao99/article/details/74910650#comments

目录(?)[+]

算法

牛客网编程题常见的编译错误：

（1）常常有逻辑是对的，但是打印时没有输出结果的情况

原因：一般是输入的测试数据有多组，但编写的程序中没有使用循环接收输入数据，直接收了一组测试数据造成的；

（2）对于二叉树等类似题型，提示堆栈溢出，递归或循环超出范围的情况

原因：一般是首次进入树序列时没有判断树的根节点是否为空；

算法描述问题：

答：描述算法的方法有多种，常用的有自然语言、结构化流程图、伪代码和PAD图等，其中最普遍的是流程图。
算法描述：

自然语言    也就是文字描述；

流程图　　特定的表示算法的图形符号；

伪语言　　包括程序设计语言的三大基本结构及自然语言的一种语言；

类语言　　类似高级语言的语言，例如，类PASCAL、类C语言。

算法复杂度问题：

1）对数据进行压缩存储可以降低算法的空间复杂度；

2）算法的复杂度与问题的规模（即复杂度表达式的n）成正比

3）关于算法时间复杂度和空间复杂度：
答：对于三个复杂度符号：可以简单的理解为θ是一个区间，O是上限（也就是最坏情况），Ω为下限（相当于最好情况），都是描述随输入量n的增长算法所花费的时间的增长情况。而一般情况下，我们都是使用o来表示复杂度（即最差的情况）。
时间复杂度计算方式：寻找算法中执行频度最高的那个语句，算出其执行次数F(n)，去掉F(n)的系数可得到f(n)，那么时间复杂度就是o(f(n))，其中n趋于无穷大。一般情况下，对于n趋于无穷大时，若频次始终是常数的，那么f(n)=1，所以时间复杂度为o(1)；若频次是跟n为线性关系，那么f(n)=n，即时间复杂度为o(n)；其他以此类推。

空间复杂度计算方式：类似于时间复杂度计算。

空间复杂度包括：程序执行时所需要的存储本身指令、常数、变量和输入数据的空间，和一些对数据进行操作的工作单元、计算所需的辅助空间等。主要如下两部分：

① 固定部分。这部分空间的大小与输入/输出的数据的个数多少、数值无关。主要包括指令空间（即代码空间）、数据空间（常量、简单变量）等所占的空间。这部分属于静态空间。

② 可变空间，这部分空间的主要包括动态分配的空间，以及递归栈所需的空间等。这部分的空间大小与算法有关。

一个算法所需的存储空间用f(n)表示。S(n)=O(f(n))　　其中n为问题的规模，S(n)表示空间复杂度。

更详细解释见链接内容：http://www.cnblogs.com/songQQ/archive/2009/10/20/1587122.html

1、各种排序算法

答：常用的几种排序算法可参考：https://zhuanlan.zhihu.com/p/27232454

内部排序：内排序是指待排序列完全存放在内存中所进行的排序过程，适合不太大的数量序列；

外部排序：指数据量过大，内存不能完全存储而需要访问外存数据的排序。

稳定排序：指相同的两个元素在排序前后，其相对位置关系不变；
不稳定排序：排序前后，相同元素相对位置关系发生改变；
教科书上的八种排序算法，按稳定排序和不稳定排序分类：
稳定排序：插冒归基
不稳定排序：快选堆希

其中8种排序方式的时间复杂度和空间复杂度如下表：

注：基数排序的时间复杂度一般也可表示为O(r*n)，当r较小时就近似为O(n)；

如上表所示：

（1）冒泡、选择、直接插入排序统称为简单排序，时间复杂度均为O(n^2)；

（2）希尔排序的时间复杂度与比较步长有关，一般可认为O(n^1.3)；

（3）选择排序和堆排序的时间复杂度与初始序列排列顺序无关；

（4）空间复杂度有3个不是o(1)，分别是快、归、基，其中快排又是相对较小的。

（5）比较排序的时间复杂度最多可以减少到O(nlogn)，基数排序不是比较类排序，所以可以做到O(n)；

（1）直接插入排序

答：①就是对一段数据序列，从第一个开始像摸扑克牌时那样插入排序，如下图：

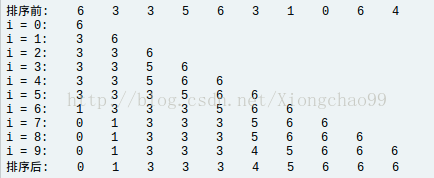
所以其时间复杂度=O(n^2)；

插入排序实现代码参考：

 void insertion_sort(vector<int> &v)  //插入排序算法
 {
     int temp = 0;
     for (int i = 1; i <= v.size(); i++)
     {
         if (v[i - 1] > v[i])
         {
             temp = v[i];
             for (int j=i-1; j > =0 && v[j] > temp; j--)
             {
                 v[j+1] = v[j];
             }
             v[j+1] = temp;
         }
     }
 }

②直接插入排序的优化：在查找插入位置时使用二分查找法，因为前面都是有序序列，使用二分查找法速度更快；

（2）希尔排序

答：希尔(Shell)排序又称为缩小增量排序，它是一种插入排序。它是直接插入排序算法的一种威力加强版，即把原来的比较步长加大。排序如下例子：

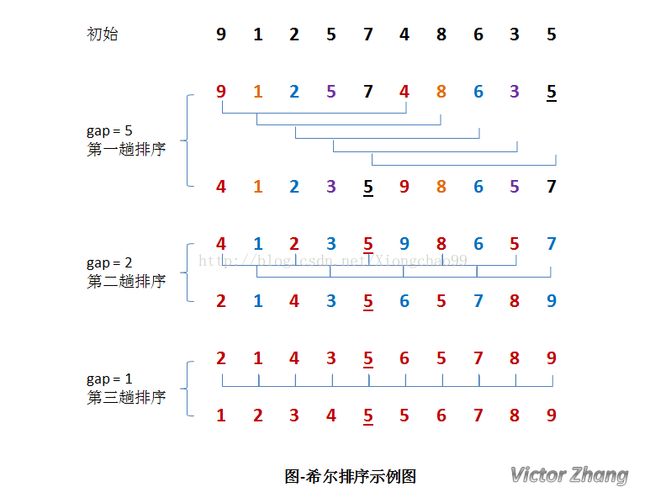
如上图，初始时，有一个大小为 10 的无序序列。

在第一趟排序中，我们不妨设 gap1 = N / 2 = 5，即相隔距离为 5 的元素组成一组，可以分为 5 组。

接下来，按照直接插入排序的方法对每个组进行排序。

在第二趟排序中，我们把上次的 gap 缩小一半，即 gap2 = gap1 / 2 = 2 (取整数)。这样每相隔距离为 2 的元素组成一组，可以分为 2 组。

按照直接插入排序的方法对每个组进行排序。

在第三趟排序中，再次把 gap 缩小一半，即gap3 = gap2 / 2 = 1。 这样相隔距离为 1 的元素组成一组，即只有一组。

按照直接插入排序的方法对每个组进行排序。此时，排序已经结束。

需要注意一下的是，图中有两个相等数值的元素 5 和 5 。我们可以清楚的看到，在排序过程中，两个元素位置交换了。

所以，希尔排序是不稳定的算法。

时间复杂度：希尔排序的时间复杂度跟比较步长的选择有关，一般可以做到O(n^1.3)；

代码实现：

 void ShellInsert(vector<int> &v, int step)//比较希尔排序代码与简单插入排序代码的异同
 {
     int temp=0;
     for(int i=step; i
        {
         if(v[i]
                {
             temp=v[i];
             for(int j=i-step; j>=0 && v[j]>temp; j=j-step)
                        {
                 v[j+1]=v[j];
             }
             v[j+1]=temp;
         }
     }
 }
 void ShellSort(vector<int> v, vector<int> step)//最终排序
 {
     //按增量数组step依次对序列做希尔排序
     for(int i=0; i
     {
         ShellInsert(v, step[i]);
     }
 }

（3）冒泡排序

答：①冒泡排序是数据前后相邻数据比较，前比后大则两者交换，之后继续向后推进比较，一轮下来最大的数据会出现在序列最后。普通的冒泡排序时间复杂度始终是n^2。实现代码略；

②针对冒泡排序的改进，即某一趟冒泡排序后没有任何元素交换位置，则结束排序——设标志位。改进部分如下：

 void(vector<int> v)
 {
     bool flag=false;
     for(int i=0; i
     {
     for(int j=0; j
     {
         if(v[j] > v[j+1])
         {
         if(v[j] > v[j+1])
         {
             swap(v[j],v[j+1]);
             flag=true;//有交换就将标志位置位
         }
         }
     }
     if(!flag)//若一趟结束都没有一次交换，表示序列已经有序
         break;
     }
 }

（4）快速排序

答：确定一个基数，先从后向前寻找一个比基数小的数（若没找到，就继续找），交换。然后转换比较方向，从前向后直到找到比基数大的，交换；再重复前面的过程。快排具体实现就是：从右找到第一个小于poviot（一般取序列中第一个数）的数，与之交换，同时left加1；然后再从左找到第一个大于poviot的数，与之交换，同时right减1；这样循环往复，直到与poviot比较的左右数据的下标相同(left=right)为止，此时poviot右边的数都大于左边，左边的数都大于右边。（注意：无论poviot被移到哪个位置，都是和它作比较）
例如：取key=49
49 38 65 97 76 13 27 原始数组 k=49
27 38 65 97 76 13 49 l=0,r=6（从后向前）
2738 65 97 76 13 49 l=1,r=6（从前向后，未找到）
27 38 49 97 76 13 65 l=2,r=6（从前向后）
27 38 13 97 76 49 65 l=2,r=5（从后向前）
27 38 13 49 76 97 65 l=3,r=5（从前向后）
27 38 13 49 76 97 65 l=3,r=4（从后向前，未找到）
27 38 13 49 76 97 65 l=3,r=3（从后向前，未找到）

注意：快速排序中最快速情况是：每一趟排序的基准值（一般第一个数据）都可以在一趟排序完成后，将当前序列平均分为两个个数相等的序列。最差的情况是，每次选取的基准数据都是当前序列中最小或最大值，即当前序列是有序序列，此时其会退化为冒泡排序。简单总结：快排相比其他排序算法最具优势的情况是数值序列完全无序，最不具优势的情况是数值序列基本有序；

代码：

 "font-size:14px;">void quicksort(vector<int> &v,int left, int right)
 {
     if(left < right)//false则递归结束
     {
         int key=v[left];//基数赋值
         int low = left;
         int high = right;
         while(low < high)    //当low=high时，表示一轮分割结束
         {
             while(low < high && v[high] >= key)//v[low]为基数，从后向前与基数比较
             {
                 high--;
             }
             swap(v[low],v[high]);

             while(low < high && v[low] <= key)//v[high]为基数，从前向后与基数比较
             {
                 low++;
             }
             swap(v[low],v[high]);
         }
         //分割后，对每一分段重复上述操作
         quicksort(v,left,low-1);
         quicksort(v,low+1,right);
     }
 }

快排更多详情参考：http://blog.csdn.net/xiongchao99/article/details/74524807#t3

（5）选择排序

       ①每一次都遍历数据序列，从待排序的数据元素中选出最小（或最大）的一个元素，顺序放在被排序序列第一个位置，直到全部待排序的数据元素排完（第一轮：用第一个数与后面数据比较，后面小就与之交换位置，继续用交换后的第一个和后续数据比较……，第二轮：用第二个数据和后面比较，类似第一轮方式，……，直到比较完所有数据）。 选择排序是不稳定的排序方法。总的比较次数N=(n-1)+(n-2)+...+1=n*(n-1)/2，与数据的初始排列顺序无关。实现代码略。

      ②除此之外还有树形选择排序，即锦标赛排序。如一个数据序列中找出最大的和第二大的数，用竞标赛思想解决最好：如有序列ABCDEFGH共8个数据的序列，找出最大和第二大的两个，需要比较的次数，见下图：

由图可知，找最大值用了7次比较，第二大值用了2次比较，共计用9次比较。

实现代码略；

（6）堆排序

答：堆排序是树形选择排序的改进型，其避免了后者较大的空间复杂度；

注意：使用的最小/最大堆都是完全二叉树；

首先可以看到堆建好之后堆中第0个数据是堆中最小的数据。取出这个数据，再根据章节二中数据结构的堆删除方式，执行下堆的删除操作并进行堆恢复工作。这样堆中第0个数据又是堆中最小的数据，重复上述步骤直至堆中只有一个数据时就直接取出这个数据。
       由于堆也是用数组模拟的，故堆化数组后，第一次将A[0]与A[n - 1]交换，再对A[0…n-2]重新恢复堆。第二次将A[0]与A[n – 2]交换，再对A[0…n - 3]重新恢复堆，重复这样的操作直到A[0]与A[1]交换。由于每次都是将最小的数据并入到后面排好序的数据序列前面，故操作完成后整个数组就有序了。注意使用最小堆排序后是递减数组，反之，最大堆排序后是递增数组。
堆顶删除后的排序也可见下例：

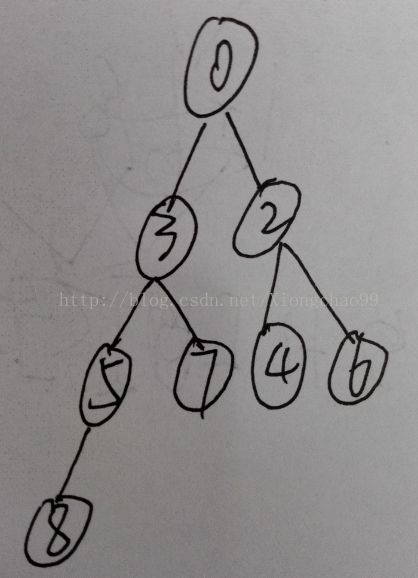根据堆的删除规则，删除操作只能在堆顶进行，也就是删除0元素。
然后让最后一个节点放在堆顶，做向下调整工作，让剩下的数组依然满足最小堆。
删除0后用8填充0的位置，为[8,3,2,5,7,4,6]
然后8和其子节点3,2比较，结果2最小，将2和8交换，为：[2,3,8,5,7,4,6]
然后8的下标为2，其两个孩子节点下标分别为2*2+1=5,2*2+2=6
也就是4和6两个元素，经比较，4最小，将8与4交换，为[2,3,4,5,7,8,6]
这时候8已经没有孩子节点了，调整完成。
每次堆删除后的堆恢复时间复杂度为O(logn)，堆排序总时间复杂度=O(nlogn)；空间复杂度=O(1);

代码实现（以最大堆为例，排序后是递增序列）：

 //注意：为了计算方便，默认数组从下标1开始，即数组v的首元素空着；
 void HeapAdjust(vector<int> v, int start, int end)//start是待调整堆的堆顶元素下标，end即为待调整堆的最后一个元素下标
 {
     int top=v[start];
     for(int j=2*start; j<=end; j=2*j)
     {
         if(j
             j++;
         if(top
         {
             v[start]=v[j];
             start=j;
         }
         else
             break;
     }
     v[start]=top;
 }

 void HeapSort(vector<int> &v) //最终排序
 {
     //建堆（从下往上进行子堆调整即可实现）
     for(int i=v.size()/2; i>0; i--)  //i=v.size()/2是倒数第二层的最后一个非叶子节点
         HeapAdjust(v, i, v.size()); //本来end应该是当前子堆的最后一个元素，但使用整堆的最后一个元素下标依然可以；

     //取堆顶元素与堆末尾交换并调整剩下的前半部分堆元素
     for(int j=v.size(); j>=1; j--)
     {
         swap(v[1], v[j]);
         HeapAdjust(v, 1, j-1);
     }
 }

（7）归并排序

答：n个元素k路归并排序的归并趟数：s=logk(n)；常见的归并排序是2路归并排序，其时间复杂度=log(n)，空间复杂度=O(n)；

排序过程：步骤一， 先将序列中的数据从中间平分为两组，然后每组再平分为两组，……，以此类推，直到最后每组只有一个元素为止；步骤二，两两相邻组进行归并排序成一组，再将归并后的紧邻两组作为一个新的组合进行归并排序，依次类推，直至序列变为一个组为止。

代码实现：

 //归并两个子序列
 void Merge(vector<int> v1, vector<int> &v2, int start, int mid, int end)     //用一个序列装两组数组，使用start、mid、end区分不同序列
 {
      //将分组v1[start,...., mid]与分组v1[mid+1, ... ,end]归并为一个数组序列
      int i=start, j=mid+1,k=0;
      while(i<= mid && j<=end )
      {
        if(v1[i]
         v2[k++]=v1[i++];
        else
         v2[k++]=v1[j++];
      }
      if(i<=mid)
       v2[k, ... ,end]=v1[i, ... ,mid];  //简要表示
      else if(j<=end)
       v2[k, ... ,end]=v1[j, ... ,end];  //简要表示
      //将排好序的新序列v2覆盖到原序列v1中
      v1[start, ..., end]=v2[0, ..., v2.size()-1];  //简要表示
 }
 //最终排序（先分割再归并，递归实现）
 vector<int> v2;     //创建辅助数组（最终长度为n）
 void MergeSort(vector<int> &arr, int start,int end)
 {
      if(start
      {
            int mid=(start+end)/2;
            MergeSort(arr, start, mid);   //递归生成左子节点（分割出左序列）
        MergeSort(arr, mid+1, end);   //递归生成右子节点（分割出右序列）
        Merge(arr, v2, start, mid, end);   //对树当前层上述两个序列进行归并
      }
 }

在归并排序中，本意是归并后的辅助空间v2作为下一个归并的源序列，然后再开辟加倍大小的空间作为新的辅助空间，这样实际的空间复杂度会是O(nlogn)；为了避免空间复杂度过大，本例采用如下方式：

只在开始开辟了一个长度为n的数组v2作为辅助空间，后面的归并都是将排好序的子序列覆盖到原始数组相应位置，然后仍然以原始数组作为归并的源序列，这样辅助空间v2就还可以作为辅助空间使用。所以可以做到空间复杂度=O(n)；

上述排序中的第二个函数使用递归实现序列分割与归并，原理可见下图：

或见下图：

--------------------------上述7个排序是比较排序，其时间复杂度的极限是O(nlogn)，下面将介绍非比较排序，时间复杂度可达到O(n)---------------------------

计数排序——时间复杂度O(k+n)，要求：被排序的数是0~k范围内的整数。一般情况下k较小，所以时间复杂度=O(n)；
基数排序——时间复杂度O(d(k+n))，要求：d位数，每个数位有k个取值。一般情况下k和d较小，所以时间复杂度=O(n)；
桶排序——时间复杂度O(n)，要求：被排序数在某个范围内，范围过大的话桶的个数会过多；

总结：非比较排序的时间复杂度都可以达到O(n)，但其空间复杂度都比较高，就是所谓的用空间换时间；

（8）基数排序

答：多关键字排序，举例说明：

①书上举例是扑克牌排序：四种花色“梅花<方块<黑桃<红桃”，纸牌面值“2<3<..... 先按面值分为13堆，再将这些堆按顺序叠加在一起，最后按花色从前面扑克牌中按顺序抽取出来存放即可；

②本例以常见的3位数以下的整数排序为例：每个数据的个、十、白位分别作为一个关键字，那么每个数据有三个关键字。

基数排序（radix sort）属于「分配式排序」，有点类似 「桶排序」，排序方式如下：

1°、分配10个桶,桶编号为0-9,以个位数数字为关键字依次入桶，将桶里的数字顺序取出来；
2°、再次入桶,不过这次以十位数的数字为关键字，进入相应的桶，同一桶内有序；
3°、再次按顺序取出，排序完成；

注意：比较顺序必须是个、十、百，否则无法比较出结果； 数据序列最大为4位、5位或更多位数的以此类推。

代码实现：

此处不写具体代码，但注意“10个桶可以直接用二维数组表示，如上序列有5个数据，桶就可以为v[10][5]”。同时，每个桶都可以重复使用后，只需要在下一轮按顺序读出数据后将桶复位为空即可；

时间复杂度=O(n)，空间复杂度=O(r*n+d*n)，其中r是关键字取值个数，d是关键字种类数；

补充：链式基数排序——将待排序序列用链表存储，解决原基数排序空间复杂度较高的困境，可以做到空间复杂度为常数（前提是原序列是用链表存储）。

补充两个排序：计数排序与桶排序，两者是在基数排序前提出的，也是上述基数排序的基础；

（9）计数排序

计数排序基本思想：输入一个数X，确定小于X的元素的个数，这样，就可以把这个数放在输出数组的指定位置上。假设输入数组是A[n]，则需要一个辅助数组C[0...k]，一个输出数组B[n]。其中，k代表输入数组中的最大值，n代表输入数组的长度。输入数组A是待排序排序的数据，输出数组B是需要排序完成后的数据，辅助数组中是按键值存储该键值在输入数组中出现的次数。

优点：时间复杂度=O(n)，对于最大元素的值较小时，使用计数排序是极快的；

缺点：空间复杂度较高，若排序数组最大值为1000，就需要一个长度为1001的数组作为辅助数组。所以，计数排序不适合数值较大的情况。

（10）桶排序（bucket sort）

答：计数排序是假设输入的数据都属于一个小区间内的整数，而桶排序则假设输入是由一个随机过程产生的。该过程将元素均匀、独立的分布在区间[0,1）上。桶排序的过程可如下：

①将[0,1)平分为10（其他数字也可）个区间，即创建10个桶，然后遍历序列，将相应数据添加到各个桶中；

②使用其他比较排序方式如快排对每个桶排序；

③按桶的顺序和桶中数据存放顺序依次读出所有数据，排序完成。

2、KMP算法

答：（1） KMP算法是字符串匹配算法，它由简单字符串匹配（BF）转化而来。其中，若串长为n，模式串长为m，则
BF算法（普通匹配算法）：时间复杂度O(m*n)；空间复杂度O(1)；
KMP算法：时间复杂度O(m+n)；空间复杂度O(n)；
KMP算法需要模式函数值数组next[m]，用于辅助。

例如，在S=”abcabcabdabba”中查找T=”abcabd”，如果使用KMP匹配算法，当第一次搜索到S[5] 和T[5]不等后，S下标不是回溯到1，T下标也不是回溯到开始，而是根据T中T[5]==’d’的模式函数值（next[5]=2，为什么？后面讲），直接比较S[5] 和T[2]是否相等，因为相等，S和T的下标同时增加;因为又相等，S和T的下标又同时增加，最终在S中找到了T。如图：

所以，KMP算法相比普通匹配算法最大的优点就是： 主字符串S的指针不需要回溯。

（2）next数组求取方法：

KMP的next数组求解就是求解模式串相同前缀后缀的过程：

①取i=0元素以前的子串，求解其前缀后缀相同的个数，记为nx[0]；

②取i=1元素以前的子串，求解其前缀后缀相同的个数，记为nx[1]；

以此类推，……

③将nx数组每个元素分别右移一位，数组首元素赋值-1，得到的新数组就是next（注：得到的next是对应模式串下标从0开始的情况）；

KMP算法详情参见：http://blog.csdn.net/xiongchao99/article/details/73381280#t12

3、折半查找法（二分查找法）

答：要求：

1.必须采用顺序存储结构；

2.必须按关键字大小有序排列（不一定要升序）。

方法：取正中间进行比较，小则丢掉正中间被比较数大的一侧所有数据，继续采用二分查找比较小的一侧数据。查找中，偶数个数据取正中间靠近起始方向的数据比较，奇数个数据取正中间的。

时间复杂度：o(lgN)

4、蚂蚁爬行算法

答：n只蚂蚁以每秒1cm的速度在长为Lcm的竹竿上爬行。当蚂蚁看到竿子的端点时就会落下来。由于竿子太细，两只蚂蚁相遇时，它们不能交错通过，只能各自反方向爬行。对于每只蚂蚁，我们只知道它离竿子最左端的距离为xi，但不知道它当前的朝向。请计算所有蚂蚁落下竿子的最短时间和最长时间。
问题的要点：蚂蚁相遇后反方向爬行当做穿透对方继续爬行。故最大时间就是离某一端点最远的蚂蚁用时，最小时间则为离某端点最近的蚂蚁用时中的最大者。

5、汉诺塔（Hanoi塔）

问题：汉诺塔问题中有三根杆子A，B，C。A杆上有N个(N>1)穿孔圆盘，盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至C杆：

①每次只能移动一个圆盘；

②每个杆上大盘不能叠在小盘上面；

③根据A上原有圆盘个数k，要完成A上所有圆盘移出至C需要移动次数为。

汉诺塔移动次数的公式：f(k+1)=2*f(k)+1；（其中，f⑴=1,f⑵=3,f⑶=7）

为什么呢？假设有4个圆盘，那么移动过程可以如下描述：

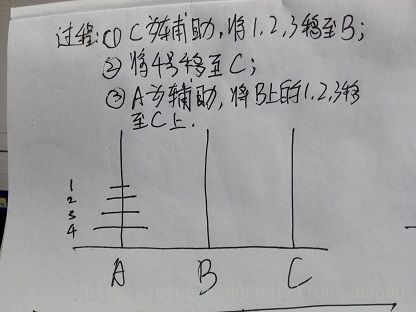
①中其中将1,2,3号移动到B，移动次数为f(3)；

②中只是将最底下的圆盘移动到空杆C上，那么移动次数就是1；

③中将A作为辅助，移动B上的1,2,3号到C上，移动次数同①，仍然为f(3)；

故总次数为：f(4)=2*f(3)+1;

以上移动流程具有普适性，可以推广到k=n，故可得公式：f(k+1)=2*f(k)+1。

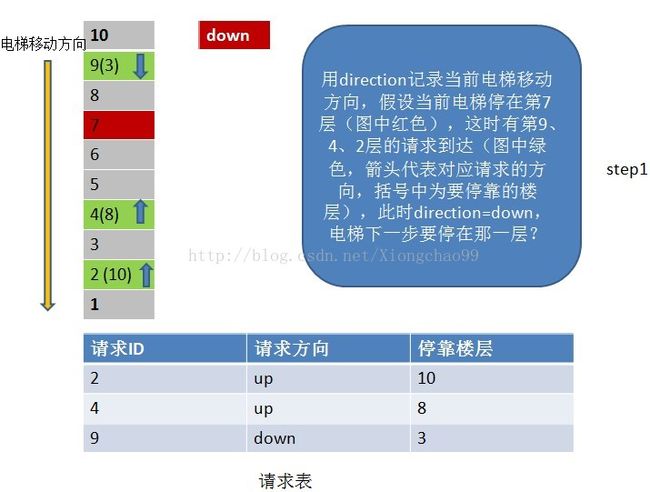
6、常见的电梯调度算法

答：电梯调度算法：

1）电梯有移动方向，各楼层的请求有请求方向，这里维护一个请求表（记录请求ID，请求方向，该请求的停靠楼层）；

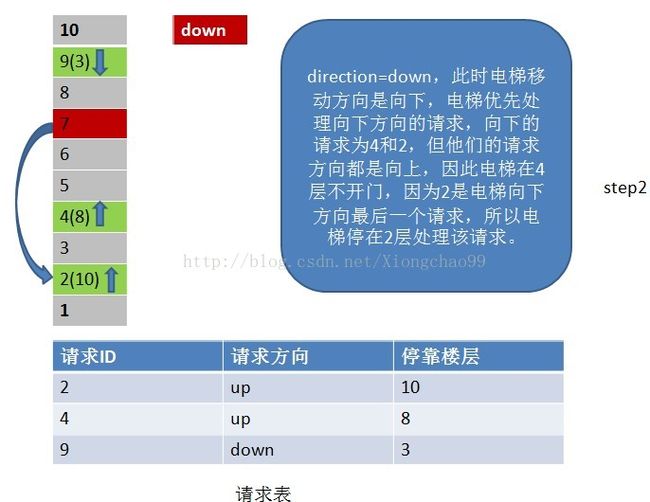
2）电梯按照一个方向移动，直到该方向没有请求，不会根据某一层的请求方向突然改变电梯的移动方向。但是注意：电梯在移动过程中只处理与“电梯移动方向”相同请求方向的请求。如电梯向下移动，只处理电梯下方楼层的请求，且该请求的方向也向下（停靠楼层请求无方向）。若请求楼层在向下方向，但请求方向不是向下，是不做处理的；

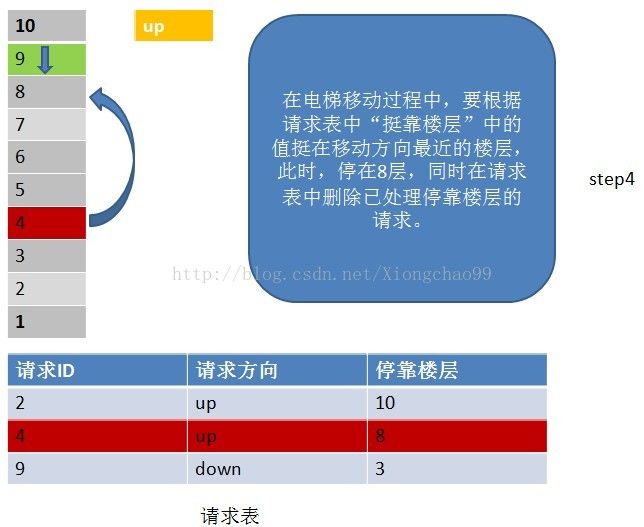
3）没完成一个请求，就从请求表中删除该请求记录；

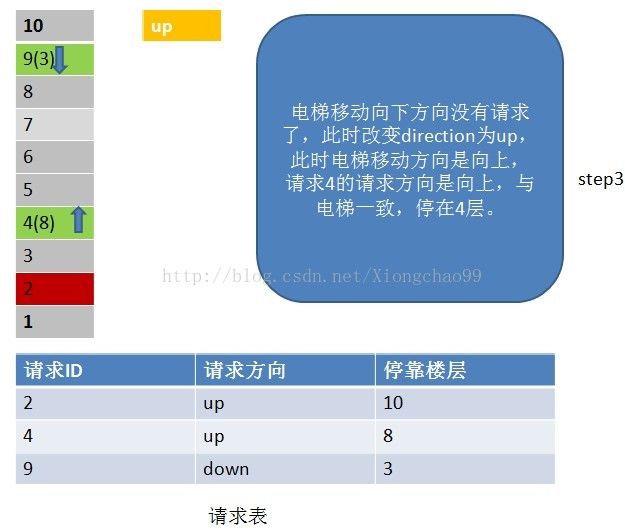
4）若移动方向上已经没有请求（这个请求不仅包括请求表中的请求楼层，还包括停靠楼层），但电梯移动方向的反方向有请求，就把电梯移动方向置位为反方向；

实际上，电梯调度算法和一些操作系统调度算法如磁盘寻道是类似的。

请看下面例子：

7、动态规划（DP）问题

答：动态规划算法通常基于一个递推公式及一个或多个初始状态。当前子问题的解将由上一次子问题的解推出。使用动态规划来解题只需要多项式时间复杂度，因此它比回溯法、暴力法等要快许多。

基本原理：首先，要找到某个状态的最优解，然后在它的帮助下，找到下一个状态的最优解。

基本思路：我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表（二维数组）中。这就是动态规划法的基本思路。具体的动态规划算法多种多样，但它们具有相同的填表格式。

经典例子解释：

（1）01背包问题

题目：一个旅行者准备随身携带一个背包，可以放入背包的物品有n种，每种物品的重量和价值分别为wj， vj。 如果背包的最大重量限制是b，怎样选择放入背包的物品以使得背包的价值最大？

目标：

约束条件：

递推公式和边界约束方程：

上述公式用C++代码表示：

i是物件编号，j是背包允许的重量，dp是最大价值数组；

dp[i][0]={0};

dp[0][j]={0};

dp[i][j] = Max（dp[i - 1][ j ]，dp[ i - 1 ][  j- weight[ i ] ]+ value[ i ]）;//注意，此语句前要添加if(j>=weght[i])判断语句。

上述所有的元素都存储在dp数组中，后续需要只需直接取出即可；

该算法的代码实现就是通过对dp[][]二维数组进行操作实现的，具体就是使用两个for的嵌套循环，实现代码（C++）如下：

 for(int i=1;i<=N;i++)
 {
         for(int j=1;j<=M;j++)
         {
                  if(v[i]<=j)
                  {
                         dp[i][j] = dp[i-1][j-v[i]]+v[i]>dp[i-1][j] ? dp[i-1][j-v[i]]+v[i]:dp[i-1][j];
                  }
                  else
                         dp[i][j]=dp[i-1][j];
          }
 }

其中，dp[][]数组存储的就是价值，i是物件编号，j是允许的最大重量，v是单件价值；

01背包的内存优化：

由dp[i][j] = Max（dp[i - 1][ j ]，dp[ i - 1 ][  j- weight[ i ] ]+ value[ i ]）可知，dp[i][j]的计算只和dp[i-1]相关，即没有使用其他子问题， 因此在存储子问题的解时，只存储dp[i-1]子问题的解即可，这样可以用两个一维数组解决，一个存储子问题，一个存储正在解决的子问题，如predp[ ]存储子问题，dp[ ]存储当前的。进一步思考，由于我们可以使得j由大到小递减变化（与上一个未优化内存的不同），而计算dp[i][j]时又只使用了dp[i-1][0……j]，没有使用dp[i-1][j+1]，即j值指向一个方向变化，这样的话，我们先计算j的循环时，让j=M……1，只使用一个一维数组即可。

代码如下：

 for (int i=1; i<=N; i++)
         for (int j=M; j>=1; j--)
         {
             if (weight[i]<=j)
             {
                 f[j]=max(f[j],f[j-weight[i]]+value[i]);  //被修改的f[j]这一轮循环后续部分就不会再用了，所以直接用一个数组即可
             }
         }

（2）完全背包问题

完全背包相对于01背包的区别是每种物品不止一件，可能有无限件，这样背包问题就可以用下面状态转移方程：

f[i][j]=Max( f[i-1][j]，f[i-1][ j - k*weight[i] ] + k*value[i])，其中0<=k<=V/weight[i+1]；

即将原来选或者不选第i种物品改为选0、1、……、k件第i种物品；

该算法的代码实现就是通过对dp[][]二维数组进行操作实现的，具体就是使用三个for的嵌套循环，实现代码（C++）：

 for (int i=1; i<=N; i++)
         for (int j=1; j<=M; j++)
         {
             for(int k=1;k
             {
                    if (k*weight[i]<=j)
                   {
                         f[i][j]=max(f[i-1][j],f[i-1][j-k*weight[i]]+k*value[i]);
                   }
                   else
                        break;
               }
         }
 }

完全背包内存优化：

1）直接筛选法：完全背包问题有一个很简单有效的优化，是这样的：若两件物品i、j满足v[i]<=v[j]且w[i]>=w[j]，则将物品j去掉，不用考虑，代码略；

2）转化为01背包问题：将同种物品中每件物品提升为每种物品；

举例：物品个数N = 3，背包容量为V = 5。

拆分之前的物品序列：

拆分之后的物品序列：

根据上述思想：在背包的最大容量（5）中，最多可以装入1件物品一，因此不用扩展物品一。最多可以装入2件物品二，因此可以扩展一件物品二。同理，可以扩展一件物品三。

最后，对拆分拓展后的物品序列进行01背包计算即可。

代码实现如下（与01优化背包相同）：

 for (int i=1; i<=N; i++)
         for (int j=M; j>=1; j--)
         {
             if (weight[i]<=j)
             {
                 f[j]=max(f[j],f[j-weight[i]]+value[i]);
             }
         }

8、英语句子按单词为单位逆序

答：一般逆序操作都可以用栈实现；

例如C++中：

定义string类型的栈：stack st;

以及3个常用函数：

string str;

push(str);  //将字符串压栈

pop(str);  //将字符串弹出栈

top(); //返回栈顶元素的引用（注意，此处返回的是栈顶的字符串）

9、根据3条边求三角形面积——海伦公式

答：如下，3边长为：m_a, m_b, m_c，海伦公式为：

s=(m_a+m_b+m_c)/2;  
area=sqrt(s*(s-m_a)*(s-m_b)*(s-m_c));

实现主要代码：

 if((m_a+m_b>m_c) && (m_a+m_c>m_b) && (m_b+m_c>m_a))  //这个判断一定需要有
 {
          double s=(m_a+m_b+m_c)/2;   //算法主要部分
          double area=sqrt(s*(s-m_a)*(s-m_b)*(s-m_c));
 }

10、回文序列相关问题

答：回文序列是指字符串正着读和反着读都是一样的。

（1）字符串是否回文串的判断：

使用栈进行操作——若字符串序列长度为偶数，则将串的前一半依次压入栈中，在依次弹出并与剩下的一般字符串按顺序依次比较，若对应都相同，则该字符串为回文序列。若串长为奇数个，则直接舍掉中间那个，其他按照偶数个操作即可；

（2）字符串最大回文子串查找：

注意区分： 最大回文子序列和最大回文串，前者相邻元素在原串中可以不连续（只保证顺序一致即可），后者在原串中必须是连续的；

1）蛮力法：

时间复杂度为o(n^3)——先将字符串的所有子串求出来，然后对每个子串判断是否为回文串（子串判断是否为回文串使用（1）中方式）；

大致写一下过程：

cin>>s;   //输入字符串

int  maxlen=0;

int n=s.size();

string str;

int count=0;

int p,q=0;

for(int i=0;i

      for(int j=i;j

             str=s.substr(i,j-i+1);

             p=0;

             q=str.size()-1;    //截取子串

             while(p

                   if(str[p]!=str[q]){

         break;

                   } 

                   p++;q--;              

             }

             if(maxlen

                   maxlen=str.size();

             count++;

      }

}

2）蛮力法改进：

说明： 回文串必定是对称的，所以可以一一遍历每个元素，对各个元素进行左右对应数判断是否相等，记录每次遍历得出的回文长度；

过程： 由于回文对称轴有两种情况，①回文长度为奇数，对称轴是正中间元素；②回文长度为偶数，对称轴是正中间间隙；

为了统一成奇数长度，我们对回文可做改变如：ABCBA -> #A#B#C#B#A#，ABBA -> #A#B#B#A#，这样偶数长度变为了奇数长度，奇数长度的还是奇数长度，不用再考虑对称轴在中间间隙的情况了；

时间复杂度o(n^2)—— 相对于蛮力法，其避免了一些重复的比较，减小了时间复杂度；

实现代码如下：

 int maxLen2(string str)
 {
     string s;
     //添加辅助符#
     s.push_back('#');
     for(int k=0;k
         s.push_back(str[k]);
         s.push_back('#');
     }
     cout<

     //依次把每个字符作为对称中心进行最长回文判断
     int len = s.size();
     int maxlen=0;
     for (int i = 1; i < len-1; i++)  //s的首尾都是#，不属于原字符串，可不计算
     {
         int count=1;
         while(i-count>=0&&i+count<=len-1 && s[i-count]==s[i+count]){
                 count++;
         }
         if(maxlen
             maxlen=count-1;
     }
     return maxlen;
 }

3）manacher算法

第二种方法中改进算法的时间复杂度还是不够好，可以继续改进，就是manacher算法，可得到时间复杂度为o(n)；

算法的核心：用辅助数组p记录以每个字符为核心的最长回文字符串半径（也就是p[i]记录了以str[i]为中心的最长回文字符串半径。p[i]最小为1，此时回文字符串就是字符串本身），再结合“一个大回文串对称轴的左右两侧分别有一个子串，且这两个子串的位置相对大回文串对称轴对称，则其中一个子串是回文，另一个子串一定也是回文”的原理，免去重复计算；

算法核心图示：

假设mx记录了前期比较结果中拥有最大右边界回文子串的右边界位置，pi记录该回文字符串对称轴位置：

如上如所示，i和j关于pi对称，若在上述拥有最大有边界的蓝色文串范围内，以j为对称轴处有一个回文子串，那么i为对称轴处也必然有一个回文子串（关于pi的两侧是对称的）。这样便可减少当前i对称轴的回文比较次数，即j处会问半径为p[j]，那么i对称轴会问判断就直接从i+p[j]-1开始判断（说明：公式i的对称位置j=2*pi-i；）；

但是有另外一种情况，就是j的一部分超出蓝色部分，这时p[i]=p[j]就不一定对了，在使用i+p[j]-1前就一定要进行范围判定，如下图 ：

实现代码：

 int maxLen3(string str)
 {
     string s;
     //添加辅助符#
     s.push_back('#');
     for(int k=0;k
         s.push_back(str[k]);
         s.push_back('#');
     }
     cout<

     //依次把每个字符作为对称中心进行最长回文判断
     int len = s.size();
     //以下为相比野蛮改进法新增的参数
     int *p = new int[len];  //辅助数组（记录每个点为对称轴的回文长度）
     p[0] = 1;
     int mx =0, pi=0;//边界和对称中心
     for(int i=1;i//s的首尾都是#，不属于原字符串，可不计算
     {
         if(mx>i)
         {
             p[i]=min(mx-i+1,p[2*pi-i]);//核心
         }else{
             p[i]=1;
         }

         while(i-p[i]>=0&&i+p[i]<=len-1 && s[i-p[i]]==s[i+p[i]]){
             p[i]++;
         }

         if(i+p[i]-1 > mx){
             mx = i+p[i]-1;
             pi = i;
         }
     }
     //最大回文字符串长度
     int maxlen = 0;
     for(int i=1;i
     {
         if(p[i]>maxlen)
         {
             maxlen = p[i];
         }
     }
     delete []p;
     return maxlen-1;
 }

注意比较maxLen2和maxLen3的区别：主要就是将maxLen2中的count，在maxLen3中用数组存储起来了，用于后面减少回文子串开头重复的比较次数；

（3）一个字符串最少需要删掉几个字符才能构成成回文串：

解释：求删除最少元素后的最大回文串实际就是求取一个字符串的最大回文序列，故可用动态规划方式；

过程：

       首先，是将该字符串逆序，采用#include库的reverse(s.begin(),s.end())函数得到逆序的s；

       然后，然后对原字符串s0和逆序字符串s采用如下计算字符串相同子串序列公式（动态规划公式）进行判断：

                 A=a1a2……aN，表示A是由a1a2……aN这N个字符组成，Len(A)=N;

                 B=b1b2……bM，表示B是由b1b2……bM这M个字符组成，Len(B)=M.
                定义LCS(i,j)=LCS(a1a2……ai,b1b2……bj)，其中0≤i≤N，0≤j≤M.
                对于1≤i≤N，1≤j≤M，有公式:
                若ai=bj，则LCS(i,j)=LCS(i-1,j-1)+1；
                若ai≠bj，则LCS(i,j)=Max(LCS(i-1,j-1),LCS(i-1,j),LCS(i,j-1))；

      最后，对于长度为len的字符串，最后返回len-LCS(len,len)就是最少需要删除的字符数。

对于上述相同子序列计算（动态规划）公式的应用，需要设置一个矩阵（代码中用二维数组表示）来进行统计，该部分参考代码如下：

注意：  MaxLen的大小应该是(length1+1)* (length2+1)，字符串下标0对应MaxLen中的下标1，而MaxLen下标0的数据作为辅助求取MaxLen中下标1的元素，从而保证MaxLen[i - 1][j], MaxLen[i][j - 1]不会溢出；可参见图片：

 #include
 #include
 #include
 #include
 using namespace std;

 int maxLen(string s1, string s2){
     int length1 = s1.size();
     int length2 = s2.size();
     vectorint> > MaxLen(length1+1,vector<int>(length2+1));  //也可以用指针来定义二维动态数组

     for (int i = 1; i <= length1; ++i)
     {
         for (int j = 1; j <= length2; ++j)
         {
             if (s1[i-1] == s2[j-1]){
                 MaxLen[i][j] = MaxLen[i-1][j - 1] + 1;
             }
             else{
                 MaxLen[i][j] = max(MaxLen[i - 1][j], MaxLen[i][j - 1]);
             }
         }
     }
     return MaxLen[length1][length2];
 }

 int main(){
     string str;
     while(cin>>str){
         string str0=str;
         reverse(str.begin(),str.end());
         cout<
     }
 }

11、素数统计

答：有两种方法：筛选法和开根号法；
筛选法：从小到大筛去一个已知素数的所有倍数。依次删除可被2整除，3整除……的数字，剩下的则为素数 。

开根号法：如果一个数大于2，对这个数求平方根，如果这个数能被这个数的平方根到2之间的任何一个（只要有一人就行）整除说明就不是质数，如果不能就说明是质数（开根号法时间复杂度小一些，只有筛选法的一半）。

筛选法是原理：所有非素数都是素数的乘积构成的；

开根号法原理：假如一个数N是合数，它有一个约数a,a×b=N，则a、b两个数中必有一个大于或等于根号N，一个小于或等于根号N。因此，只要小于或等于根号N的数（1除外）不能整除N，则N一定是素数。

总结：两者原理其实大同小异，后者是在前者基础上改进而来。

筛选法举例：

 void getPrime0(int n){
      int i,j;
      bool m;
      for(i = 1; i <= n; i ++){
            m = true;
            for(j = 2; j < i; j ++){
                  if(i % j == 0){
                       m = false;
                       break;
                  }
            }
            if(m){
                  cout << i << " ";
            }
      }
      cout << endl;
 }

事实上，上述j应该换为n前的所有素数集合中的一员，所以需要数据存取操作，此处为了方便没有用该操作，而是直接使用所有的n前数据。

开根号法举例：

 bool prime(int x)
 {
      int y;
      for(y=2;y<=sqrt(x);y++)
          if (x%y==0)
             return false;
      return true;
 }

以上是使用开根号算法的素数判断函数。

12、小明走台阶问题——一个楼梯有n级，小明一次最多跨3级，问小明走完台阶有多少种走法？

答：（1）这是一个递归问题，但可以用循环实现：
首先，假设走法总数为f(n)，那么f(1)=1,f(2)=2,f(3)=4；

当n>3，有如下递归关系：

f(n)=f(n-1)+f(n-2)+f(n-3)，因为把爬n级台阶的最后一步分类，则 f(n-1)代表最后一步是爬1级的所有走法，f(n-2)代表最后一步是爬2级的所有走法，f(n-3)代表最后一步是爬3级的所有走法，因此关系式成立。所以：

n>3，f(n)=f(n-1)+f(n-2)+f(n-3)；
注意：这是一次最多跨三级，如果只能跨两级就需要做相应改变。
f(1)=1
f(2)=2
f(3)=4
f(4)=7
f(5)=2*7-f(1)=13
f(6)=2*13-f(2)=24
f(7)=2*24-f(3)=44
f(8)=88-f(4)=81
f(9)=2*81-f(5)=149
f(10)=298-f(6)=274
f(11)=548-f(7)=504
f(12)=1008-f(8)=927
f(13)=1854-f(9)=1854-149=1705
f(14)=3410-f(10)=3410-274=3136
f(15)=6272-f(11)=6272-504=5768
……

代码实现（一个循环语句搞定）：

 int climbStairs(int n){
     vector<int> v;
     v.push_back(1);
     v.push_back(1);
     for(int i = 2; i <= n; i++){
         v.push_back(v[i - 1] + v[i - 2]);
     }
     return v[n];
 }

（2）斐波那契查找

斐波那契查找是对斐波那契数列进行查找，斐波那契序列非常类似上述走台阶的序列：

F0=0，F1=1，Fn=Fn-1+Fn-2（n>=2）；

13、给定n个数的进栈序列，求出栈序列有多少种类型——卡特兰数

答：n个数有多少种出栈序列，用卡特兰数求：

f(n)=f(0)f(n-1)+f(1)f(n-2)+f(2)f(n-3)+……+f(n-2)f(1)+f(n-1)f(0)；其中，f(0)=f(1)=1；

所以，如果有一入栈序列为e1,e2,e3,e4,e5，那么出栈序列就有f(5)=42种。

14、快慢指针——判断循环链表及其他

答：快慢指针中的快慢指的是移动的步长，即每次向前移动速度的快慢。例如可以让快指针每次沿链表向前移动2，慢指针每次向前移动1次。

（1）快慢指针可以用于判断单循环链表：让快慢指针从链表头开始遍历，快指针向前移动两个位置，慢指针向前移动一个位置：

1）如果快指针到达NULL，说明链表以NULL为结尾，不是循环链表；

2）如果 快指针追上慢指针，即快指针=慢指针，则表示出现了循环。

3）为什么慢指针步长为1的话，快指针步长就为2：因为只有fastStep-slowStep=1，才能实现快慢指针一定相遇，而不是快指针越过慢指针。

代码实现如下：

 int isExitsLoop(LinkList* L) {
     LinkList *fast, *slow;
     fast = slow = L;
     while (fast!=NULL && fast->next!=NULL)
     {
         slow = slow->next;
         fast = fast->next->next;
         if (slow == fast)
         {
             break;
         }
     }
     return ((fast == NULL) || (fast->next == NULL));
 }

快慢指针用于判断有无环，有时候还要判断环的入口位置（尤其是单链表局部环入口），这种情况参考另一博文：http://blog.csdn.net/xiongchao99/article/details/74524807#t15

（2）快慢指针获取链表中间节点

使用快慢指针同时出发，当快指针到达终结点时慢指针刚好到达中间节点。

15、寻找二叉树中两个节点的最近祖先节点

答：1）若二叉树是二叉排序树（或叫做二叉查找树、二叉搜索树）：

直接前序遍历，找到一个节点m，满足n1

2）若为普通二叉树：

①树节点结构体中给定父节点指针

如：

struct node{

Node * left; 
Node * right; 
Node * parent; 

}

则算法思想：首先给出p的父节点p->parent，然后将q的所有父节点依次和p->parent作比较，如果发现两个节点相等，则该节点就是

最近公共祖先，直接将其返回。如果没找到相等节点，则将q的所有父节点依次和p->parent->parent作比较，直到p->parent==root。

程序实现如下：

 Node * NearestCommonAncestor(Node * root,Node * p,Node * q)
 {
     Node * temp;
          while(p!=NULL)
     {
         p=p->parent;
         temp=q;
         while(temp!=NULL)
         {
             if(p==temp->parent)
                 return p;
             temp=temp->parent;
         }
     }
 }

②若未给定父节点指针

算法思想：如果一个节点的左子树包含p，q中的一个节点，右子树包含另一个，则这个节点就是p，q的最近公共祖先。

程序实现：

 /*查找a，b的最近公共祖先，root为根节点，out为最近公共祖先的指针地址*/
 int FindNCA(Node* root, Node* a, Node* b, Node** out)
 {
     if( root == null )
     {
         return 0;
     }

     if( root == a || root == b )
     {
         return 1;
     }

     int iLeft = FindNCA(root->left, a, b, out);
     if( iLeft == 2 )
     {
         return 2;
     }

     int iRight = FindNCA(root->right, a, b, out);
     if( iRight == 2 )
     {
         return 2;
     }

     if( iLeft + iRight == 2 )
     {
         *out = root;
     }
     return iLeft + iRight;
 }

用递归方式实现对树一层一层的访问，若left+right=2，那么表示当前节点就是最近祖先节点。

16、双栈排序

答：例如，实现栈数据的升序排列，即栈顶数据最大。

思路：利用一个辅助栈，每次比较排序栈和辅助栈的顶元素，如果排序栈较小直接压入辅助栈，并弹出排序栈，否则将辅助栈的元素弹出并压在排序栈栈顶元素的后面。如此反复，直到排序栈没有元素了，之后将辅助栈的元素全部导入排序栈，就完成排序。

程序实现：

 class TwoStacks {
 public:
     vector<int> twoStacksSort(vector<int> numbers) {
             stack<int> mystack,help;
             for(auto i=numbers.end()-1;i>=numbers.begin();--i)
                 mystack.push(*i);
             while(!mystack.empty())
                 {
                 if(help.empty()){
                     help.push(mystack.top());
                     mystack.pop();
                 }
                 else if(mystack.top()<=help.top())
                     {
                     help.push(mystack.top());
                     mystack.pop();
                 }
                 else
                     {
                     int temp=mystack.top();
                     mystack.pop();
                     mystack.push(help.top());
                     mystack.push(temp);
                     help.pop();
                 }
             }
         while(!help.empty())
             {
             mystack.push(help.top());
             help.pop();
         }
         for(auto &c:numbers)
             {
             c=mystack.top();
             mystack.pop();
         }
         return numbers;
     }
 };

17、判断一个二叉树结构是否为另一个二叉树的子结构

答：一般算法分为两个步骤：

（1）第一步在树A中找到和B的根节点的值一样的结点R；
（2）第二步再判断树A中以R为根结点的子树是不是包含和树B一样的结构。

C++实现代码如下：

 /*
 struct TreeNode {
     int val;
     struct TreeNode *left;
     struct TreeNode *right;
     TreeNode(int x) :
             val(x), left(NULL), right(NULL) {
     }
 };*/
 class Solution {
 public:
     bool HasSubtree(TreeNode* pRoot1, TreeNode* pRoot2)
     {
             bool flag=false;

             if(pRoot1!=NULL && pRoot2!=NULL)
             {
                 if(pRoot1->val==pRoot2->val)  //判断根节点，相等就继续判断其他节点是否相等
                     flag=Match(pRoot1,pRoot2);
                 if(!flag)       //否则判断左儿子节点是否与子结构根节点相等
                     flag=HasSubtree(pRoot1->left,pRoot2);
                 if(!flag)       //还不等，则判断右儿子节点是否与子结构根节点相等
                     flag=HasSubtree(pRoot1->right,pRoot2);
             }
             return flag;
     }



     bool Match(TreeNode* root1,TreeNode* root2){
         if(root1 == NULL && root2 != NULL) return false;
         if(root2 == NULL) return true;
         if(root1->val != root2->val) return false;
         //if(root1->val == root2->val)
         return Match(root1->left, root2->left)&&Match(root1->right, root2->right);
     }
 };

18、DFS

答：以二叉树为例（就是二叉树的先根遍历），其他树或图的DFS在此基础上进行改进。实现代码如下：

①递归方式十分简单：

 void preorder(TreeNode root){
     if(root){
         cout<data<<' ';
         preorder(root->lchild);
         preorder(root->rchild);
     }
 }

②非递归方式：需要使用栈作为辅助，两个循环实现；

 while(t || s.empty!=True){
     while(t){    //只要结点不为空就应该入栈保存，与其左右结点无关
         cout<data<<' ';
         push(&s,t);
         t= t->lchild;
     }
     t=pop(&s);
     t=t->rchild;
 }

19、BFS——队列辅助

答：以二叉树为例（就是二叉树按层遍历），其他树或图的BFS在此基础上进行改进。使用队列queue实现，每当从队列头部弹出一个节点，就将该节点的子节点按先左后右的方式压入队尾；实现代码如下：

 /*
 struct TreeNode {
     int val;
     struct TreeNode *left;
     struct TreeNode *right;
     TreeNode(int x) :
             val(x), left(NULL), right(NULL) {
     }
 };*/
 class Solution {
 public:
     vector<int> PrintFromTopToBottom(TreeNode* root) {
         vector<int> v;
         queue q;
         if(root==NULL)
             return v;

         q.push(root);
         while(q.size()>0){

             int data=q.front()->val;
             v.push_back(data);

             if(q.front()->left!=NULL)
                 q.push(q.front()->left);
             if(q.front()->right!=NULL)
                 q.push(q.front()->right);
             q.pop();
         }
         return v;
     }
 };

20、贪心算法

答： 所谓贪心算法是指总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的 仅是在某种意义上的局部最优解。

一、贪心算法的基本思路：
1.建立数学模型来描述问题。
2.把求解的问题分成若干个子问题。
3.对每一子问题求解，得到子问题的局部最优解。
4.把子问题的解局部最优解合成原来解问题的一个解。

二、贪心算法适用的问题
贪心策略适用的前提是：局部最优策略能导致产生全局最优解。
实际上，贪心算法适用的情况很少。一般，对一个问题分析是否适用于贪心算法，可以先选择该问题下的几个实际数据进行分析，就可做出判断。

例如，常见的背包问题对于贪心算法看似适用，其实是不适用，比如：物品A、B、C的价值为30、20、10，质量为30、20、10。若背包最大承重为28，那么按照贪心算法应该取单位质量价值最高者，但三者价质比都为1，所以无法选择，若任意选择，选A错，选C不是最佳结果；

三、贪心算法的实现框架
如下：

从问题的某一初始解出发；
while （能朝给定总目标前进一步）
{ 
利用可行的决策，求出可行解的一个解元素；
}
由所有解元素组合成问题的一个可行解；

四、常见的贪心算法应用

（1）最小生成树的Prim算法和Kruskal算法

最小生成树：包括了加权连通图里的所有顶点，且其所有边的权值之和亦为最小；

prim算法搜索最小生成树：

设加权图的顶点集为V，边集为E，先新建一个顶点集Vnew和边集Enew，主要步骤就是重复下列操作，直到Vnew = V：

a、在集合E中选取权值最小的边，其中u为集合Vnew中的元素（已经选择过的旧顶点），而v不在Vnew集合当中（如 果存在有多条满足前述条件即具有相同权值的边，则可任意选取其中之一）；

b、将v加入集合Vnew中，将边加入集合Enew中；

Kruskal算法搜索最小生成树：

1）记Graph中有v个顶点，e个边；

2）新建图Graphnew，Graphnew中拥有原图中相同的e个顶点，但没有边；

3）将原图Graph中所有e个边按权值从小到大排序；

4）循环：从权值最小的边开始遍历每条边直至图Graph中所有的节点都在同一个连通分量中， 如果这条边连接的两个节点不在同一个连通分量中， 添加这条边到图Graphnew中；

（2）均分纸牌

有n堆纸牌，每堆纸牌数量不等，每次从任一堆中选取若干张纸牌，移到自己相邻的堆中。例如：有4个堆，分别有9、8、17、6张纸牌，现进行移动最少次数使得每堆纸牌数相等；

算法：

从左向右遍历，当有一堆不足均值，就从右边相邻的取，大于均值就将多余的纸牌移动到右边相邻的堆上；

如上举例：

①从②取1张，②从③取三张，③向④送4张，④不变，结束；用了三次移动，是最少的情况。

（3）最大整数

设有n个正整数，将它们连接成一排，组成一个最大的多位整数。
例如：n=3时，3个整数13，312，343，连成的最大整数为34331213。
又如：n=4时，4个整数7，13，4，246，连成的最大整数为7424613。

算法：

从左到右，依次进行“先把整数转换成字符串，然后在比较a+b和b+a，如果a+b>=b+a，就把a排在b的前面，反之则把a排在b的后面”。

如上举例：

"13312"<"31213"，故取结果为后者，接着"31213343"<"34331213"，也取结果为后者；

21、比较钻石重量（笔试编程题）

答：题目如下：

小明陪小红去看钻石，他们从一堆钻石中随机抽取两颗并比较她们的重量。这些钻石的重量各不相同。在他们们比较了一段时间后，它们看中了两颗钻石g1和g2。现在请你根据之前比较的信息判断这两颗钻石的哪颗更重。
给定两颗钻石的编号g1,g2，编号从1开始，同时给定关系数组vector,其中元素为一些二元组，第一个元素为一次比较中较重的钻石的编号，第二个元素为较轻的钻石的编号。最后给定之前的比较次数n。请返回这两颗钻石的关系，若g1更重返回1，g2更重返回-1，无法判断返回0。输入数据保证合法，不会有矛盾情况出现。
测试样例：2，3，[[1，2]，[2，4]，[1，3]，[4，3]]，4
返回：1

思路：设法将大于g1的所有元素存入max中，小于g1的元素存入min中，然后查看g2在max还是min中；

实现代码如下：

 int cmp(int g1, int g2, int records[][2], int n)
 {
     // write code here
     vector<int> max, min;
     //先直接根据含有g1的比较组，将大于g1的值添加到数组max，小于g1的值添加到数组min
     for (int i = 0; i < n; i++)
     {
         if (records[i][0] == g1)
         {
             min.push_back(records[i][1]);
         }

         if (records[i][1] == g1)
         {
             max.push_back(records[i][0]);
         }
     }

     //然后根据重量大小关系的传递性，循环比较，向max中添加比max已有元素还大的值，向min中
     //添加比min已有元素还小的值
     int count = 0;
     while (count < n) //为什么要比较n轮：最坏的情况是每轮只有比较序列中最后一对某元素被添加，故
     {                //需要n轮才可以保证添加完整性
         count++;
         for (int i = 0; i < n; i++)
         {
             if (records[i][0] != g1 && records[i][1] != g1)
             {
                 if (find(min.begin(),min.end(),records[i][0])!=min.end()) //原有min数组中发现当前数值对较大者
                     min.push_back(records[i][1]);
                 if (find(max.begin(),max.end(),records[i][1])!=max.end()) //原有max数组中发现当前数值对较小者
                     max.push_back(records[i][0]);
             }
         }
     }

     if (find(max.begin(),max.end(),g2)!=max.end() && find(min.begin(),min.end(),g2)==min.end())
         return -1;
     else if (find(max.begin(),max.end(),g2)==max.end() && find(min.begin(),min.end(),g2)!=min.end())
         return 1;
     else
         return 0;
 }

22、任意进制之间互相转换

答：题目描述
将一个处于Integer类型取值范围内的整数从指定源进制转换为指定目标进制； 可指定的进制值范围为[2,62]； 
每个数字位的可取值范围为[0-9a-zA-Z]； 输出字符串的每一个都须为有效值；反例："012"的百位字符即为无效值。 实现时无需考虑非法输入。

输入描述:
输入为：
源进制 目标进制 待转换的整数值
例子：8 16 12345670

输出描述:
整数转换为目标进制后得到的值

输入例子:
8 16 12345670

输出例子:
29cbb8

思路：这类进制转换的题目一般是先转化为十进制，然后将十进制转化为目标进制（即：以十进制作为桥梁）

代码实现：

 #include
 #include
 using namespace std;

 int main(){
     int source,target=0;
     string str;
     while(cin>>source>>target>>str){
         int DecNum=0;
         //区分正负数
         int i=0;
         if(str[0]=='-')
             i=1;
         else
             i=0;

         //转化为10进制
         while(i
             int num=0;
             DecNum=DecNum*source;
             if(str[i]<='9')
                 num=str[i]-'0';
             else if(str[i]>='a' && str[i]<='z')
                 num=str[i]-'a'+10;
             else if(str[i]>='A' && str[i]<='Z')
                 num=str[i]-'A'+36;

             DecNum+=num;
             i++;
         }

         //10进制转化为目标进制
         string tStr;
         while(DecNum>0){
             string temStr;
             int num=DecNum%target;
             if(num<=9)
                 temStr=std::to_string(static_cast<long long>(num));   //VS2010未实现int转化为string
             else if(num>=10 && num<=35)
                 temStr='a'+num-10;
             else if(num>=36 && num<=61)
                 temStr='A'+num-36;
             tStr=temStr+tStr;

             DecNum=DecNum/target;
         }
         if(str[0]=='-')
             tStr="-"+tStr;
         cout<
     }
 }

23、链表反转

答：链表反转最典型的的方式就是使用三个指针p、q、r，前两个用于当前反转的两个节点，第三个用于保存后续待反转的第一个节点。注意，r指针的必须的，否则q的反转会造成q->next丢失。实现代码如下：

 ListNode* ReverseList(ListNode* pHead) {
     ListNode *p,*q,*r;
     if(pHead==NULL || pHead->next==NULL){
         return pHead;
     }else{
         p=pHead;
         q=p->next;
         pHead->next=NULL;
         while(q!=NULL){
             r=q->next;
             q->next=p;
             p=q;
             q=r;
         }
         return p;
     }
 }

24、统计二进制中有多少个1

答：这类算法题是非常普遍的，解法也有多种，在此介绍3种（注意：以下算法对正负整型数都适用）：

①直接统计二进制每位是否为1（用求余法，和十进制统计每位一样）

 int Count1(unsigned int v)
 {
     int num = 0;
     while(v)
     {
          if(v % 2 == 1)
          {
               num++;
          }
          v = v/2;
     }
     return num;
 }

②右移法（每次右移前统计最后一位是否为1）

 int Count2(unsigned int v)
 {
     unsigned int num = 0;
     while(v)
     {
          num += v & 0x01;
          v >>= 1;
     }
     return num;
 }

③依次清除最右位1法（使用减1和&实现清除，每清除一次统计数加一）

 int Count3(unsigned int v)
 {
     int num = 0;
     while(v)
     {
          v &= (v-1);
          num++;
     }
     return num;
 }

25、复杂链表复制

答：复杂链表：每个节点中有节点值，以及两个指针，一个指向下一个节点，另一个特殊指针指向任意一个节点。如下：

 struct RandomListNode {
     int label;
     struct RandomListNode *next, *random;
     RandomListNode(int x) :
     label(x), next(NULL), random(NULL){
 }
 };

复杂链表复制就是指复制一个一模一样的链表，不是浅拷贝而是深拷贝。因为每个节点多了一个指向任意位置的特殊指针，常见的链表深拷贝方式（按节点对应关系一个个创建）已经不好用了，要实现复制复杂链表，最好的办法是“将新创建的节点插入到原链表对应节点的后面”，具体如下：

     1）复制节点A得到A1，将A1插入节点A后面；

     2）遍历链表，A1->random = A->random->next；

     3）将链表拆分成原链表和复制后的链表；

代码实现：

 链接：https://www.nowcoder.com/questionTerminal/f836b2c43afc4b35ad6adc41ec941dba
 来源：牛客网

     RandomListNode* Clone(RandomListNode* pHead)
     {
         if(!pHead) return NULL;
         RandomListNode *currNode = pHead;
         while(currNode){
             RandomListNode *node = new RandomListNode(currNode->label);
             node->next = currNode->next;
             currNode->next = node;
             currNode = node->next;
         }
         currNode = pHead;
         while(currNode){
             RandomListNode *node = currNode->next;
             if(currNode->random){
                 node->random = currNode->random->next;
             }
             currNode = node->next;
         }
         //拆分
         RandomListNode *pCloneHead = pHead->next;
         RandomListNode *tmp;
         currNode = pHead;
         while(currNode->next){
             tmp = currNode->next;
             currNode->next =tmp->next;
             currNode = tmp;
         }
         return pCloneHead;
     }

26、两个有序链表合并

答：题目：输入两个单调递增的链表，输出两个链表合成后的链表，当然我们需要合成后的链表满足单调不减规则。

思路：针对两个有序链表或者线性表的合并问题，一般都是定义一个数组（或者vector）v，然后根据：

 while(i
      if(a[i]>=b[j]){
           v.push_back(a[i]);
           i++;
      }
      else{
           v.push_back(b[j]);
           j++;
      }
 }

 if(i
      ……
 }
 else if(b.size()){
      ……
 }

分别将两组数据按大小顺序插入新的数组或容器中；

上述题目代码实现：

 /*
 struct ListNode {
     int val;
     struct ListNode *next;
     ListNode(int x) :
             val(x), next(NULL) {
     }
 };*/
 class Solution {
 public:
     ListNode* Merge(ListNode* pHead1, ListNode* pHead2)
     {
         if(pHead1==NULL){
             return pHead2;
         }else if(pHead2==NULL){
             return pHead1;
         }

         ListNode* pHead;
         vector v;
         int len=0;
         while(pHead1!=NULL && pHead2!=NULL){
             if(pHead1->val<=pHead2->val){
                 v.push_back(pHead1);
                 pHead1=pHead1->next;
             }else{
                 v.push_back(pHead2);
                 pHead2=pHead2->next;
             }

             len=v.size();
             if(len>=2){
                 v[len-2]->next=v[len-1];
             }
         }

         if(pHead1!=NULL){
             v[len-1]->next=pHead1;
         }else if(pHead2!=NULL)
             v[len-1]->next=pHead2;

         pHead=v[0];
         return pHead;
     }
 };

拓展：上述是常规方式，针对两个有序链表的合并，还可以使用递归实现：

 ListNode* Merge(ListNode* pHead1, ListNode* pHead2)
 {
     if(pHead1==NULL)
         return pHead2;
     else if(pHead2==NULL)
         return pHead1;
     if(pHead1->val <= pHead2->val){
         pHead1->next=Merge(pHead1->next,pHead2);
         return pHead1;
     }else{
         pHead2->next=Merge(pHead1,pHead2->next);
         return pHead2;
     }
 }

递归太强大，代码量少多了。。。

27、字符串全排列

答：全排列：对于一个序列，按照一定的排列规则（一般都是按元素字典顺序）进行排序，获得所有的排序序列。若序列有n个元素，全排列就有n!个序列组合；

举例：字符串acb的全排列就是从最小的abc开始已进行排序得到abc、acb、bac、bca、cab、cba共3!=6个；

实现方式：

（1）调用库函数： next_permutation：

对于C++的使用者，STL中的algorithm库封装了全排列函数next_permutation(str.begin(), str.end())，具体实现如下：

 vector Permutation(string str){
     vector v;
     if(str=="")
  return v;
     sort(str.begin(), str.end());//必须先递增排序，使得str是最小一种排序
     do
     {
         v.push_back(str);
     }
     while (next_permutation(str.begin(), str.end()));//每一次循环返回true表示找到了比str大的字符串

     return v;
 }

prev_permutation：

     prev_permutation和next_permutation的区别就是：next_permutation获得序列集合是按字典序或者升序进行的，而prev_permutation正好相反，是按降序获取的。例如字符串abc调用prev_permutation后返回FALSE，因为abc已经是最小组合了，acb字符串调用后就是abc；降序全排列代码如下：

 bool cmp(const char a,const char b){
     return a>b;
 }

 vector Permutation(string str){
     vector v;
     if(str=="")
          return v;
     sort(str.begin(), str.end(),cmp);//此处不同
     do
     {
          v.push_back(str);
     }
     while (prev_permutation(str.begin(), str.end()));

     return v;
 }

注意，next_permutation的参数分别是：第一个地址和最后元素的下一个地址，例如上述程序str.begin(), str.end()；或直接使用str，str+str.size()即可。

（2）自己编码：

一般分两种：非递归和递归；

①非递归（字典序法）：

【例】 如何得到346987521的下一个
1，从尾部往前找第一个P(i-1) < P(i)的位置
4 6 <- 9 <- 8 <- 7 <- 5 <- 2 <- 1
最终找到6是第一个变小的数字，记录下6的位置i-1
2，从i位置往后找到最后一个大于6的数
4 6 -> 9 -> 8 -> 7 5 2 1
最终找到7的位置，记录位置为m
3，交换位置i-1和m的值
4 7 9 8 6 5 2 1
4，倒序i位置后的所有数据
4 7 1 2 5 6 8 9
则347125689为346987521的下一个排列；

算法实现代码：

 vector permutation(string str)
 {
     vector v;
     if(str.empty())
         return v;
     int length=str.size();
     int fromIndex, changeIndex;
     sort(str.begin(), str.end());  //先升序排列，获取最小的字符串组合
     do
     {
         //保存当前获得的一种全排列组合
         v.push_back(str);

         fromIndex = length - 1;
         //(1)向前查找第一个由大变小的元素位置
         while (fromIndex > 0 && str[fromIndex] <= str[fromIndex - 1])
             --fromIndex;
         changeIndex = fromIndex;
         if (fromIndex == 0)
             break;
         //(2)向后查找最后一个大于words[fromIndex-1]的元素
         while (changeIndex + 1< length && str[changeIndex + 1] >= str[fromIndex - 1])
             ++changeIndex;
         //(3)交换两个值
         swap(str[fromIndex - 1], str[changeIndex]);
         //(4)对后面的所有值进行反向处理
         reverse(str.begin()+fromIndex, str.end());
     }
     while (true);
     return v;
  }

此方式在VS2010上可以实现，但不知道为什么牛客网上提示内存超限制，空间复杂度过大；

②递归方式

递归方法很容易理解：分别将每个位置交换到最前面位，之后全排列剩下的位。

【例】递归全排列 1 2 3 4 5
1，for循环将每个位置的数据交换到第一位
swap(1,1~5);
2，按相同的方式全排列剩余的位；

可见下图：

代码实现：

 void PermutationHelp(vector &ans, int k, string str) //遍历第k位的所有可能
     {
         if(k == str.size() - 1)
             ans.push_back(str);
         for(int i = k; i < str.size(); i++)
         {
             if(i != k && str[k] == str[i])
                 continue;
             swap(str[i], str[k]);
             PermutationHelp(ans, k + 1, str);
         }
     }

     vector Permutation(string str) {
         sort(str.begin(), str.end());
         vector ans;
         PermutationHelp(ans, 0, str);
         return ans;
     }

28、单链表的反转算法

答：思想：创建3个指针，分别指向上一个节点、当前节点、下一个节点，遍历整个链表的同时，将正在访问的节点指向上一个节点，当遍历结束后，就同时完成了链表的反转。

实现代码：

 ListNode* ReverseList(ListNode* pHead) {
     ListNode *p,*q,*r;
     if(pHead==NULL || pHead->next==NULL){
         return pHead;
     }else{
         p=pHead;
         q=p->next;
         pHead->next=NULL;
         while(q!=NULL){
             r=q->next;
             q->next=p;
             p=q;
             q=r;
         }
         return p;
     }
 }

29、栈作为辅助结构的经典算法

答：（1）括号匹配检验：若是左括号就压入栈，若是右括号就将栈顶括号弹出与右括号匹配；

（2）迷宫求解：若当前位置可通就压入栈，接着向下一个位置探索。若当前位置不可通，则读取栈顶元素，继续探索该元素其他方向的邻接位置。重复上述过程直到出口位置。

（3）算术表达式求值：使用两个栈，一个用来寄存运算符，另一个用来寄存操作数和运算结果。基本思想如下：

（4）实现一个拥有min()成员函数的栈结构：使用两个栈，其中一个用于存储所有元素，另一个用于存储每个序列对应的最小值。基本思想如下：

①当前要进栈元素<=stackMin栈顶元素时，将当前要进栈元素同时加入到stackMin中；
②当前要进栈元素>stackMin栈顶元素时，stackMin栈把当前stackMin的栈顶元素再压入一遍；

（5）两个栈实现队列的先进先出；

（6）不使用第二个栈作为辅助的情况下实现栈的反转：是用递归实现，每次递归创建一个局部变量存储一个栈元素。基本思路如下：

①递归获取栈底元素，将栈底元素取出，其他元素依次在退出递归时按原顺序压入栈；

②将上述步骤①迭代n-1次就可实现栈的反转；

获取栈底元素（步骤①）参考代码：

 int popBottom(Stack stack){
      int result = stack.pop();
      if(stack.isEmpty()){//弹出一个栈顶元素后，栈为空了，表示该元素就是栈底元素
          return result;
      }else{
          int last = popBottom(stack);
          stack.push(result);//注意！！！这里是把前面拿到的元素压入，这样栈底元素才不会再次压入到栈中
          return last;
      }
  }

（6）栈中元素 排序（最多使用一个辅助栈）：假设栈stack是存放原来数据的，再定义一个辅助栈help，先从stack栈中取出栈顶元素pop，将pop和help中栈顶元素比较，如果pop <= help栈顶元素，将pop压入到help栈中；如果pop > help栈顶元素，取出help栈顶元素，将其放入到stack栈中，直到help为空或者pop <= help栈顶元素。

30、队列作为辅助结构的经典算法

答：（1）两个队列实现栈的先进后出；

（2）树的广度优先遍历：先向队列压入第一层节点（只有一个根节点），再弹出队列头部节点（根节点）并打印，弹出节点的同时将该节点的所有子节点从左到右依次压入队列。接着又弹出头部节点并打印，同时把该节点的所有子节点都压入队列。以此类推。

（3）双端队列实现滑动窗口最大值序列获取： 双端队列保存的是数组的下标，通过插入与弹出保证队首始终是最值的下标，并且时间复杂度为O(n)。基本思路：

①窗口向前移动一个元素，先在队头执行弹出规则：若前队尾-队首元素的值==窗口大小w-1，就表示队头元素在这一轮就过期了，直接将队头元素弹出；

②在队尾执行插入规则：1°、队列为空肯定直接插入；2°、队列不空，如果队尾元素arr[qmax.peekLast]  > 当前遍历元素arr[i]，直接将下标i插入到队尾；如果队尾元素为下标所指的数组元素arr[qmax.peekLast] <= 当前遍历元素arr[i]，说明当前队尾元素下标不可能成为后面窗口的最大值了，因此直接将队尾元素弹出，再继续比较新的队尾元素所指数组元素和当前元素arr[i]，根据上面规则加入；