雷达干扰样式仿真matlab仿真
雷达干扰样式仿真matlab
- 噪声调幅干扰
- 噪声调频干扰
- 切片重构干扰
- 间歇采样转发干扰
- 梳状谱干扰
- 频谱弥散干扰
- 噪声卷积干扰
- 噪声乘积干扰
- 代码私聊
噪声调幅干扰
噪声调幅干扰（AM）的数学模型表示为：
J ( t ) = [ U 0 + K A U n ( t ) ] e x p ( ω j + ϕ ) J(t) = [U_0+K_AU_n(t)]exp(\omega_j+\phi) J(t)=[U0+KAUn(t)]exp(ωj+ϕ)
该函数表达式是一个广义的平稳随机过程，其中exp()是以e为底的指数函数， U n ( t ) U_n(t) Un(t)是零均值高斯白噪声， U 0 ( t ) U_0(t) U0(t)是载波电压，噪声的调制系数 K A K_A KA控制 U n ( t ) U_n(t) Un(t)的功率， ω j \omega_j ωj为干扰的载频相位 ϕ \phi ϕ在 [ 0 , 2 π ] [0,2\pi] [0,2π]上均匀分布，且和 U n ( t ) U_n(t) Un(t)是相互独立的随机变量。由此可知，噪声调幅干扰是一种瞄准干扰，将高斯白噪声调制到雷达的线性调频信号的带宽范围内，即利用大能量的调制噪声对雷达形成频带压制，以影响接收端对信号的检测。
（1）时域图
（2）频域图
（3）时频图
噪声调频干扰
噪声调频干扰（FM）的数学模型表示为：
J ( t ) = U j e x p [ j ( 2 π f c + 2 π K F ∫ 0 t u ( t ) d t + ϕ ) d t ] J(t) = U_jexp[j(2\pi f_c+2\pi K_F\int_0^t u(t )\,dt+\phi)dt] J(t)=Ujexp[j(2πfc+2πKF∫0tu(t)dt+ϕ)dt]
噪声调频干扰是一个广义平稳的随机过程，其中exp()是以e为底的指数函数，调制噪声 ϕ \phi ϕ是零均值高斯白噪声，在 [ 0 , 2 π ] [0,2\pi] [0,2π]上均匀分布,且和 U n ( t ) U_n(t) Un(t)是相互独立, f c f_c fc 是噪声调频信号的中心频率， K F K_F KF是调频斜率， U j U_j Uj是干扰的振幅，用于控制单位调制信号强度引起的频率的增减。有效调制系数 m f m_f mf可以由下式计算：
m f = K F / δ F n m_f=K_F/\delta F_n mf=KF/δFn
其中， δ F n \delta F_n δFn是调制噪声的带宽，有效调制系数是判断瞄准式干扰和阻塞式干扰的重要依据，当 m f > 1 m_f>1 mf>1,此时噪声调频干扰是阻塞式干扰，否则是瞄准式干扰。
（1）时域图
(2)频域图
（3）时频图
切片重构干扰
切片重构干扰是一种为了针对脉冲压缩雷达而研发的密集距离假目标干扰。该种干扰的产生原理如下：
1.由干扰机截获雷达信号，然后把信号下变频到中频信号。
2.把信号存储在数字存储器之内。
3.读取信号并进行均分的等间隔采样。
4.分段复制采样信号
其数学模型为：
J ( t ) = ∑ k = 0 n − 1 p ( t − K T / m n ) J(t) = \sum_{k=0}^{n-1}p(t-KT/mn) J(t)=k=0∑n−1p(t−KT/mn)
其中， p ( t ) p(t) p(t)表达式为：
p ( t ) = s ( t ) [ r e c t ( ( t − τ a ) / τ a ) ∗ ∑ i = 0 m − 1 δ ( t − i T a ) ] p(t) = s(t)[rect((t-\tau_a)/\tau_a)*\sum_{i=0}^{m-1}\delta(t-iT_a)] p(t)=s(t)[rect((t−τa)/τa)∗i=0∑m−1δ(t−iTa)]
其中，T表示雷达LFM信号脉宽，m表示矩形脉冲串个数，n表示每一段填充的个数， τ a \tau_a τa表示矩形脉冲串脉宽， δ ( . ) \delta(.) δ(.)表示冲击函数， T a T_a Ta表示矩形脉冲串基波周期
（1）时域图
（2）频域图
（3）时频图
间歇采样转发干扰
间歇采样转发干扰（IS）是采用DRFM干扰机对雷达信号进行间歇采样再依次转发形成的，一个采样周期中多次采样转发，就形成了IS干扰。该种干扰的数学表达式为：
J ( t ) = ∑ n = 1 N r e c t ( ( t − τ / 2 − ( n − 1 ) T s ) / T ) e j 2 π ( f 0 t + K / 2 t 2 ) J(t) = \sum_{n=1}^N rect((t-\tau /2-(n-1)T_s)/T)e^{j2\pi(f_0t+K/2 t^2)} J(t)=n=1∑Nrect((t−τ/2−(n−1)Ts)/T)ej2π(f0t+K/2t2)
其中， τ \tau τ是间歇采样的脉冲宽度，T是雷达信号的脉宽， T s T_s Ts是采样周期，则 τ / T s \tau/T_s τ/Ts表示间歇采样占空比。
（1）时域图
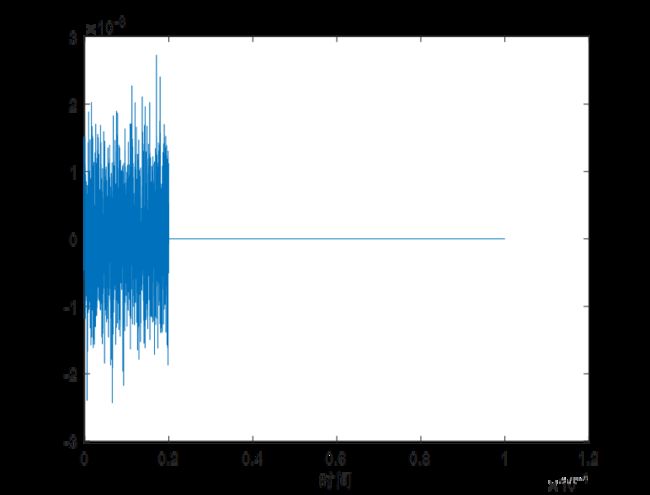
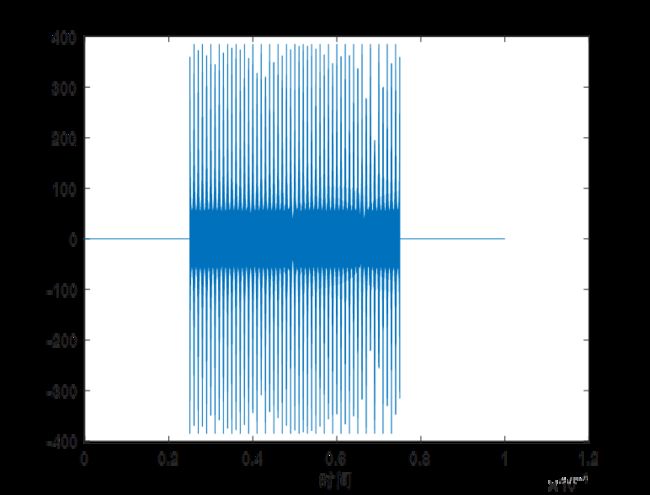
（2）频域图
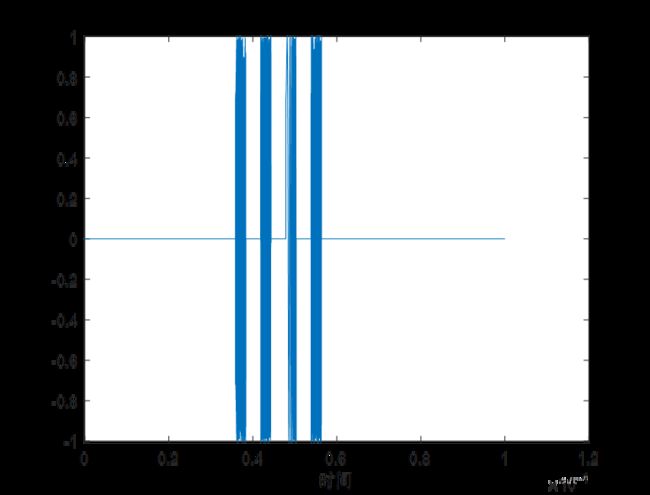
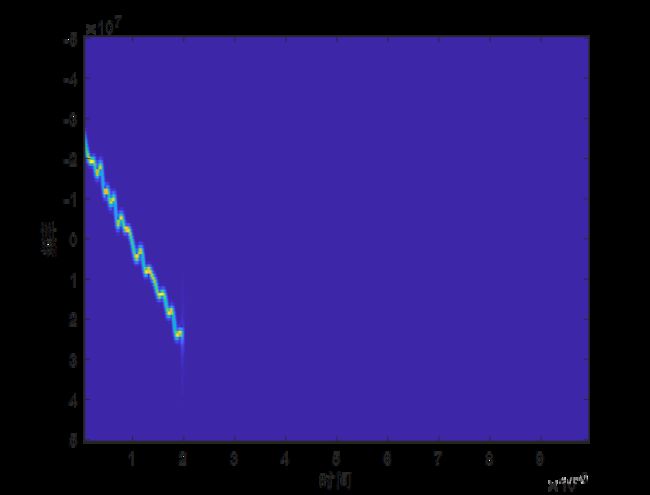
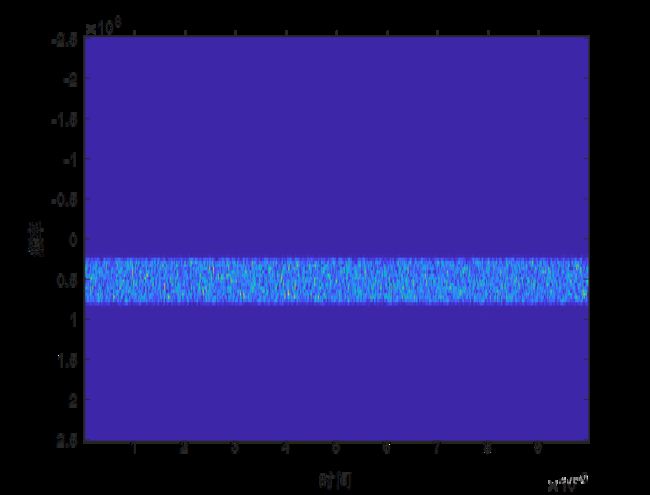
（3）时频图
梳状谱干扰
LFM信号的梳状谱（COMB）干扰的产生主要是通过梳状谱信号和线性调频信号乘积调制产生的，产生的干扰可以拥有欺骗或压制效果，梳状谱信号的表达式如下：
c o m b ( t ) = ∑ i = 1 M a i e j 2 π f i t comb(t)=\sum_{i=1}^M a_i e^{j2\pi f_i t} comb(t)=i=1∑Maiej2πfit
其中， f i f_i fi对应每个梳齿出现的频率点， a i a_i ai是第 i i i个频率点处的幅度。
因此，雷达梳状谱干扰的数学模型如下：
J ( t ) = s ( t ) c o m b ( t ) = r e c t ( t / T ) ∑ i = 1 M a i e j 2 π [ ( f 0 + f i ) t + K t 2 / 2 ] J(t)=s(t)comb(t)=rect(t/T)\sum_{i=1}^M a_ie^{j2\pi [(f_0+f_i)t+K t^2/2]} J(t)=s(t)comb(t)=rect(t/T)i=1∑Maiej2π[(f0+fi)t+Kt2/2]
间歇采样转发干扰（IS）是采用DRFM干扰机对雷达信号进行间歇采样再依次转发形成的，一个采样周期中多次采样转发，就形成了IS干扰。该种干扰的数学表达式为：
$$
（1）时域图
（2）频域图
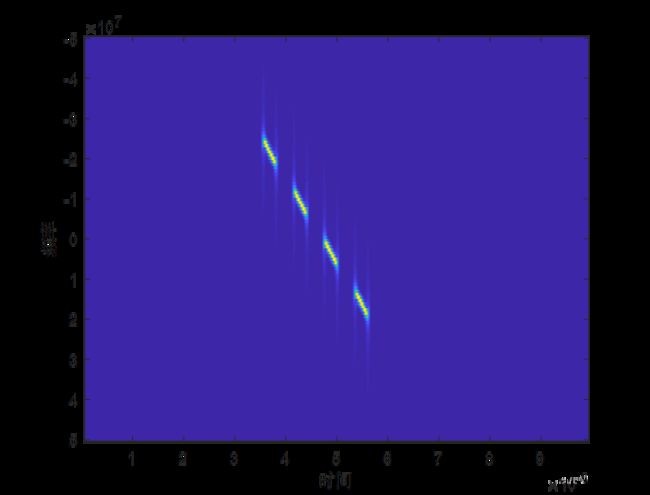
（3）时频图
频谱弥散干扰
频谱弥散干扰（SMSP）是针对LFM雷达的一种干扰，其产生过程为：干扰接收机接收到雷达发射信号后，通过混频、低通滤波、模数转换后将数据存入数字射频存储器。然后，将数据送入数据缓冲区，经过传输门并行传输到移位寄存器组，其中移位寄存器的时钟频率是控制数据送入DRFM时的时钟频率的N倍。数据重复N次后串行送入数模转换器，经混频滤波由发射机将干扰信号发射出去。干扰信号由N个子脉冲组成的调频斜率为雷达发射信号N倍的时宽不变的信号。
设雷达发射信号为LFM信号，其形式为：
S ( t ) = e j π k t 2 , k = B / T , 0 < t < T S(t)=e^{j\pi kt^2},k=B/T,0
根据SMSP信号产生原理，将时钟频率调成原频率的N倍，则得到第一个子脉冲信号为：
J 1 ( t ) = A j e j π k n t 2 , k n = N k , 0 < t < T / N J_1(t)=A_je^{j\pi k_nt^2},k_n=Nk,0
其中， A j A_j Aj为干扰信号幅度。将这一子脉冲信号重复N次即得到干扰信号时域表达式如下：
J S M S P ( t ) = ∑ i = 1 N − 1 J 1 ( t − i T / N ) = J 1 ( t ) ⨂ ∑ i = 1 N − 1 δ ( t − i T / N ) J_{SMSP}(t)=\sum_{i=1}^{N-1}J_1(t-iT/N)=J_1(t)\bigotimes \sum_{i=1}^{N-1}\delta(t-iT/N) JSMSP(t)=i=1∑N−1J1(t−iT/N)=J1(t)⨂i=1∑N−1δ(t−iT/N)
（1）时域图
（2）频域图
（3）时频图
噪声卷积干扰
噪声卷积干扰（CN，卷积调制灵巧噪声）是一种基于DRFM技术的卷积调制干扰，旨在利用目标信号产生想干干扰。雷达发射的信号被干扰机接收再放大滤波后，下变频变为中频信号然后存储到数字射频存储器（DRFM），经过一定处理后再上变频雷达信号所在频段。另一路，雷达信号经过接收和处理后，控制噪声单元产生合理长度和类型的噪声数据。两路输出信号在卷积器例完成卷积运算，最后可以产生一种效果较好的灵巧噪声干扰波形。设输入DRFM的雷达信号为 s ( t ) s(t) s(t)，延时后输出 s ( t − τ ) s(t-\tau) s(t−τ)， s ( t − τ ) s(t-\tau) s(t−τ)和 s ( t ) s(t) s(t)是相参的。窄带高斯噪声信号为 n ( t ) n(t) n(t)， s ( t − τ ) s(t-\tau) s(t−τ)与 n ( t ) n(t) n(t)卷积，进行噪声卷积调制得到输出卷积调制灵巧噪声干扰信号，其数学表达式为：
J ( t ) = s ( t − τ ) ⨂ n ( t ) J(t)=s(t-\tau)\bigotimes n(t) J(t)=s(t−τ)⨂n(t)
（1）时域图
（2）频域图
（3）时频图
噪声乘积干扰
噪声乘积干扰（NP，乘积调制灵巧噪声）产生原理域卷积调制灵巧噪声类似，设输入DRFM的雷达信号为 s ( t ) s(t) s(t)，延时后输出 s ( t − τ ) s(t-\tau) s(t−τ)， s ( t − τ ) s(t-\tau) s(t−τ)和 s ( t ) s(t) s(t)是相参的。窄带高斯噪声信号为 n ( t ) n(t) n(t)， s ( t − τ ) s(t-\tau) s(t−τ)与 n ( t ) n(t) n(t)相乘，进行噪声乘积调制得到输出乘积调制灵巧噪声干扰信号，其数学表达式为：
J ( t ) = s ( t − τ ) n ( t ) J(t)=s(t-\tau)n(t) J(t)=s(t−τ)n(t)
（1）时域图
（2）频域图
（3）时频图
