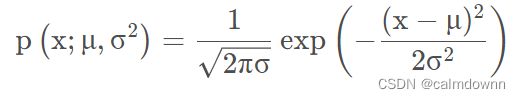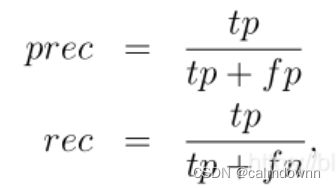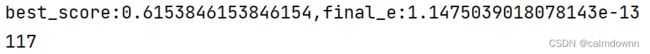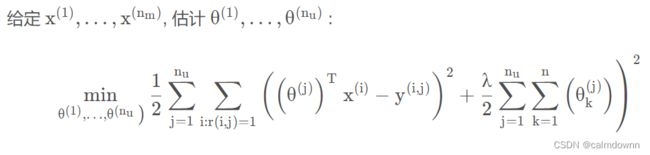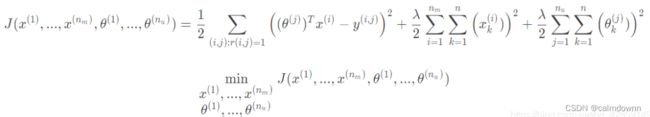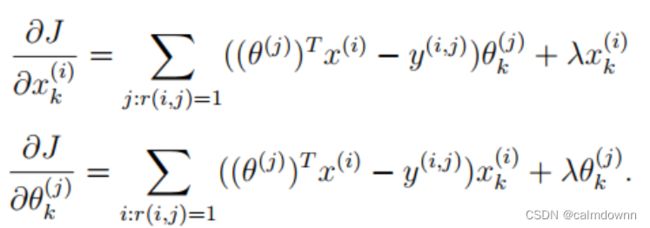【吴恩达】机器学习作业ex8--异常检测和推荐系统(Python)
一.前言
此次作业也是分为俩大部分,第一部分是利用高斯分布来检测计算机中的异常行为,每个计算机有吞吐量和响应延迟俩个特征,此次数据集分为测试集和交叉验证集,交叉验证集中的yval集合是标注是否正常或者异常,测试集中并没有此标注,需要我们来找出异常,熟练之后,还要将其应用于更高维的数据集中,第二部分是推荐系统,给一个新用户推荐10部他有可能会喜欢的电影
二.异常检测
1.ex8data1.mat代码部分
1.1 导入工具包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.io import loadmat1.2 导入数据
导入测试集和交叉验证集
data = loadmat('ex8data1.mat')
# print(data.keys()) # ['__header__', '__version__', '__globals__', 'X', 'Xval', 'yval']
Xtest = data['X']
Xval = data['Xval']
yval = data['yval']Xtest,Xval,yval的维度如下:
1.3 图像分布
从图像可以看出,有几个点的布局有点离谱,这几个离谱点一般被认为是异常点
# 看一下图像分布
def plot_pic(Xtest):
plt.figure(figsize=(13, 8))
plt.scatter(Xtest[:, 0], Xtest[:, 1], c='purple', s=150)
pass
# plot_pic(Xtest)
# plt.show()1.4 获取高斯分布的参数(平均值和方差)
平均值和方差的求法如下图:简单说一下,平均值就是当前这一列特征值的所有行数据相加和再除以行数,得到的就是此特征值的平均值,方差也是同理,用当前这一列特征值的所有行数据减取当前特征值的平均值,开平方再加到一起,最后除以行数即可
说一下代码的思想,我用的是矩阵运算方法,这样可以减少运算时间,看着也更方便,这里平均值就是利用Xtest.sum(0),意思就是对Xtest的每一列都求和,然后放入mean_matrix,这里mean_matrix矩阵的维度是1行2列(1,2),同理方差也是这个方法,套入公式返回到一个variance_matrix矩阵中,里面存放着每列特征值的方差,维度同样是1行2列(1,2)
# 获取一下高斯函数的参数
def get_gaussian_parameters(Xtest):
X_rows, X_colums = Xtest.shape
mean_matrix = Xtest.sum(0) * (1 / X_rows) # sum0是列求和,sum1是行求和,这里得到的是每个特征值的平均值mu
variance_matrix = np.power(Xtest - mean_matrix, 2).sum(0) * (1 / X_rows) # 里面存放每个特征值的方差
return mean_matrix, variance_matrix
pass
# mean_matrix,variance_matrix = get_gaussian_parameters(Xtest)
# print(mean_matrix,variance_matrix)测试集(Xtest)的平均值和方差如下:
1.5 高斯函数
高斯分布的算法如下:
高斯分布也就是正态分布,通常我们认为x符合高斯分布, x ∼ N ( μ , σ 2 ) ,概率函数如下图,注意,下图的X可以看成是Xj,也就是第i个特征向量,同理 μ 和 σ2 也是属于第j个特征值的平均值和方差
下图可以看出,μ 和 σ2 对P(Xj)的影响,μ控制中心坐标,σ2控制宽度
下面这个公式就是给定一行数据,假如此数据有n个特征值,那么就要求出每个特征值的p(xj),将这个数据所有特征值p(xj)进行练乘,就得到了最终的p(x),p(x)在三维图像上代表的就是高度,概率越大高度越高,越贴近中心,反之也成立
# 高斯函数
def get_gaussian(mean_matrix, variance_matrix, Xtest):
X_rows, X_colums = Xtest.shape
front = np.power(2 * np.pi * np.power(variance_matrix, 1 / 2), 1 / 2 * (-1)) # 公式前一部分
back = np.exp(-np.power(Xtest - mean_matrix, 2) / (2 * variance_matrix)) # 公式后一部分
p = front * back
p_matrix = np.prod(p, axis=1) # 得到一个1*307的矩阵,每一列都是已经算好的,根据公式累乘就行
return p_matrix
pass
# mean_matrix,variance_matrix = get_gaussian_parameters(Xtest)
# p_matrix = get_gaussian(mean_matrix,variance_matrix,Xtest)
# print(p_matrix)
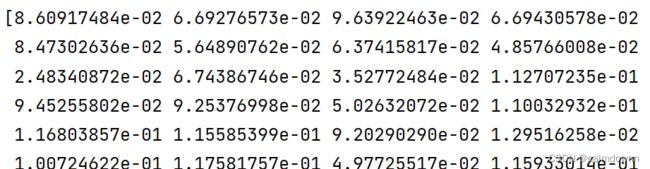
# print(p_matrix.shape,p_matrix)在这里简单说一下代码过程:我这里同样是直接用矩阵操作的,得到的p维度为307*2,行代表307行数据,2列就代表2个特征值所对应各自的概率值p(xj),每行数据总的p(x)就是其每个特征值自己的p(xj)进行相乘,所以最好用了np.prod()函数,来将矩阵p的所有列相乘得到p_matrix最终矩阵
测试集返回的p矩阵数据如下:
1.6 画高等线图
画高等线图就是为了更直观的看到概率p(x)的分布情况,简单说一下画这个图的思想:
首先创建x,y为0-30分100段的俩个轴,因为高等线图是三维状态,所以我们得将x,y俩个轴绘制成一张大网格,可以把这个网格想象成地面,np.meshgrid()作用就是绘制成网格后,返回每个网格的横纵坐标,zz就是将网格的所有横纵坐标捏和到一起,将zz传入高斯分布函数中,返回的就是当前网格的概率p,前面说过了p(x)其实就是高度,小网格的概率p(x)越大,越靠近中心,高度也越高,正常点的概率更大,反之异常点的概率更大,但判断是否异常的分界点p需要在后面找
# 画一下高等线图
def plot_countour(mean_matrix, variance_matrix, Xtest):
plt.figure(figsize=(13, 8))
x = np.linspace(0, 30, 100)
y = np.linspace(0, 30, 100)
xx, yy = np.meshgrid(x, y) # 将xy绘制成网格,xx,yy分别是网格的所有横纵坐标
zz = np.c_[xx.ravel(), yy.ravel()] # 将网格中每一个小网格的坐标都放入z中,然后进行高斯函数求值(10000,2)
p = get_gaussian(mean_matrix, variance_matrix, zz) # 高斯函数返回的是(10000,)维度的矩阵
p = p.reshape(xx.shape) # 重新绘制成网格的形态(100,100)
cont_levels = [10 ** h for h in range(-20, 0, 3)]
plt.contour(xx, yy, p, cont_levels) # xx,yy代表的是底部平面,平面由网格组成,每个网格的值也就是P值,就是高度,高度越高代表概率越大
plt.scatter(Xtest[:, 0], Xtest[:, 1], c='purple', s=100)
pass
# mean_matrix,variance_matrix = get_gaussian_parameters(Xtest)
# plot_countour(mean_matrix,variance_matrix,Xtest)
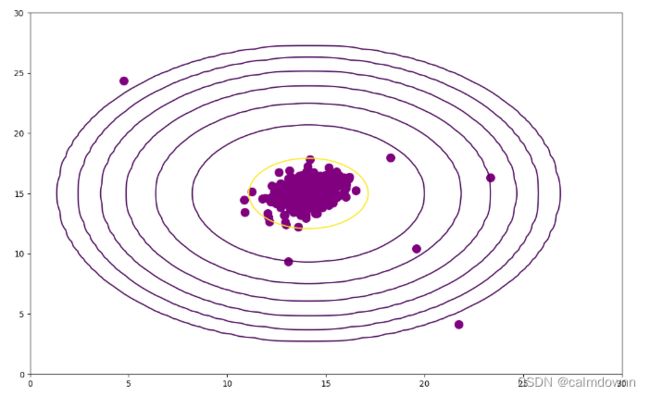
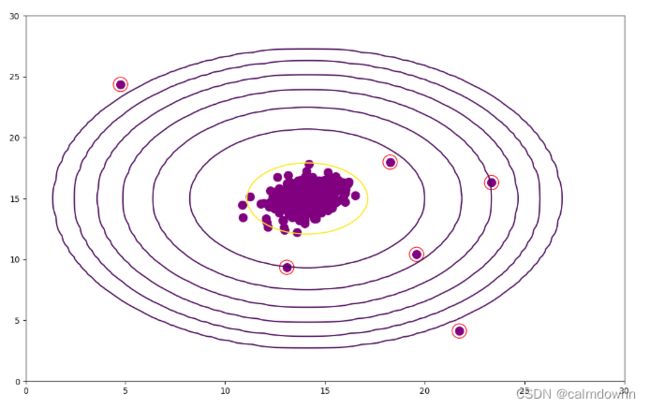
# plt.show()图中一圈一圈的就是等高线,因为这是二维图片,所以在三维图中此线是高度,被揪起来的感觉,可以看到越外圈的等高线,概率越低,高度也越低,在外圈上的点作为异常点的概率也越大
1.7 构造一个评分函数
构造评分函数的目的:
在进行高斯分布算法之后会得到矩阵p(x),里面存放着数据集集每行数据的概率,要判断是否是异常点,我们需要找出一个参数 ε ,以此作为分界点,比当前 ε 小的概率p就会被视为异常点,反之为正常点,但是这个参数 ε 需要不停的尝试才行,所以需要一个评分函数来对每一个 ε 进行评分,来取最适合的分界点
评分函数的过程:
此次用的是计算F1score的方法,需要将TP,FP,TN,FN都先计算好,注意这里计算它们一定要用交叉验证集当中的数据,因为只有交叉验证集中才有yval结果,才能进行判断操作。
下一步求出prec与rec:
最后将prec.rec带入下面公式求出f1即可
注意!!!:一定要注意分母为0的情况,将分母为0的情况做一个if 分支,不然会报错
# 下面构造一个评分函数,判断边界函数是否够好
def predict_score(p, yval, e):
p = p.reshape(yval.shape)
rows, columns = yval.shape
TP = 0
FP = 0
TN = 0
FN = 0
prec = 0
rec = 0
F1 = 0
# p ( x ) < ε 被认为异常(y = 1),p ( x ) < ε(y = 0) 被认为正常
for i in range(rows):
if (p[i, :] > e): # 预测为0
if (yval[i, :] == 0):
TN += 1 # 实际为0
else:
FN += 1 # 实际为1
if (p[i, :] < e): # 预测为1
if (yval[i, :] == 1):
TP += 1 # 实际为1
else:
FP += 1 # 实际为0
if (TP + FP):
prec = TP / (TP + FP)
if (TP + FN):
rec = TP / (TP + FN)
if (prec + rec):
F1 = (2 * prec * rec) / (prec + rec)
return F1
pass
# mean_matrix,variance_matrix = get_gaussian_parameters(Xtest)
# p_matrix = get_gaussian(mean_matrix,variance_matrix,Xval)
# F1 = predict_score(p_matrix,yval,p_matrix[0])
1.7 挑选边界 ε 值
下面就开始找最适合的参数 ε ,作为p矩阵的概率边界,这里参数范围我选择的p(x)矩阵最大值到最小值之间,分成1000段,依次带入评分函数进行评分,最后返回最好的预测分数以及参数 ε
# 下面构造select函数,用来选出最好的ε作为分解条件
def select_beste(p, yval):
p_max = np.max(p)
p_min = np.min(p)
e_list = np.linspace(p_min, p_max, 1000)
best_score = 0
final_e = p_min
for i in e_list:
cur_score = predict_score(p, yval, i)
if (cur_score > best_score):
best_score = cur_score
final_e = i
return best_score, final_e下面运行一下,注意取得平均值和方差是属于测试集的,对于高斯算法求出的概率矩阵p_matrix是属于交叉验证集的
# 取一下边界e
mean_matrix, variance_matrix = get_gaussian_parameters(Xtest)
p_matrix = get_gaussian(mean_matrix, variance_matrix, Xval)
best_score, final_e = select_beste(p_matrix, yval)
print(f"best_score:{best_score},final_e:{final_e}")1.8 找出异常点并在图像上标出
上面通过交叉验证集已经得到了最好的参数 ε (final_e),接下来先获取测试集的概率矩阵p_matrix1,用np.where()函数去筛选所有比ε (final_e)小的数据行,将这些数据行在图片上表示出来即可
p_matrix1 = get_gaussian(mean_matrix,variance_matrix,Xtest) # 这个p矩阵一定要是Xtest的
weird_point = np.where(p_matrix1 < final_e)[0]
plot_countour(mean_matrix,variance_matrix,Xtest)
plt.scatter(Xtest[weird_point,0],Xtest[weird_point,1],edgecolors='r',s=300,facecolors='none')
plt.show()2. ex8data2代码部分(高维)
2.1 导入数据
data2 = loadmat('ex8data2.mat')
# print(data2.keys()) # ['__header__', '__version__', '__globals__', 'X', 'Xval', 'yval']
X2test = data2['X']
X2val = data2['Xval']
y2val = data2['yval']
# print(X2test.shape, X2val.shape, yval.shape) # (1000, 11) (100, 11) (100, 1)X2test,X2val,yval的维度如下: 可以看出有11个特征值
2.2 找出异常点
过程还是一样的,先利用交叉验证集(X2val)找出最优的参数 ε(final_e),接下来获取测试集(X2test)的概率矩阵p_matrix1,找出异常点,展示异常点的个数
mean_matrix, variance_matrix = get_gaussian_parameters(X2test)
p_matrix = get_gaussian(mean_matrix, variance_matrix, X2val)
best_score, final_e = select_beste(p_matrix, y2val)
print(f"best_score:{best_score},final_e:{final_e}")
p_matrix1 = get_gaussian(mean_matrix,variance_matrix,X2test)
weird_point = np.where(p_matrix1 < final_e)[0]
print(len(weird_point))可以看出异常点有117个
三.推荐系统
1.前言
此部分目的是给新用户推荐10个新电影,利用以往的用户对电影的评分,通过协同过滤算法来求出X与Theta矩阵,ex8movies.mat的数据集中存放着Y矩阵(1682行*943列数据),行列分别代表了1682篇电影与943个用户,矩阵中存放的是用户对电影的打分。其中还有R矩阵(1682,943),矩阵中只有0和1俩个值,0代表用户没有看过此电影,1代表看过并且打分
2.代码部分(ex8movies.mat/ex8movies.txt)
2.1 导入包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.io import loadmat
from scipy.optimize import minimize2.2 导入数据
先导入ex8_movies.mat,将Y矩阵和R矩阵取出
data = loadmat('ex8_movies.mat')
# print(data.keys()) # ['__header__', '__version__', '__globals__', 'Y', 'R']
Y = data['Y'] # 不用用户对于不同电影的评分,行为电影数,列为用户数(维度:1682,943)
R = data['R'] # 判断是否有评分,维度与Y矩阵相同
# print(Y.shape,R.shape)其次导入ex8_movieParams.mat,这个数据集分别存放着:用户的数量,电影数量,特征数量以及电影特征值矩阵(X)和用户特征值矩阵(Theta)
data2 = loadmat('ex8_movieParams.mat')
# print(data2.keys()) # ['__header__', '__version__', '__globals__', 'X', 'Theta', 'num_users', 'num_movies', 'num_features']
X = data2['X'] # 电影类型偏向的特征值
Theta = data2['Theta'] # 用户的特征值
num_users = int(data2['num_users']) # 用户数量
num_movies = int(data2['num_movies']) # 电影数量
num_features = int(data2['num_features']) # 特征数量(X和Theta矩阵的)
# print(X.shape,Theta.shape) # (1682, 10) (943, 10)
# print(num_users,num_movies,num_features) # [943] [1682] [10]2.3 序列化参数
这里说一下为什么要序列化参数,其实就是改变矩阵的形状,我们后面会用到opt.minimize()这个函数方法,这个优化方法里面需要的参数X0一定得是一维数组(nums,),所以这里将欲求的X与Theta矩阵进行序列化,将(1682,10)(943,10)维度的俩个矩阵变成(26250,)
再说一下np.r_函数,np.r_与np.c_都是对矩阵进行合并,np_r是以行为基准进行合并,可以理解为行叠加,上下组合,np_c正相反,它是以列为基准进行合并,列叠加,左右进行组合,有一点需要注意的是当内部是俩个一维度矩阵时,np_r是将第二个一维矩阵直接加在第一个一维矩阵的屁股后面,而np_c是将俩个一维矩阵先排成N行一列的矩阵,然后将俩个矩阵结合成N行俩列的矩阵
# 更改参数形状
def change_shape(X, Theta):
return np.r_[X.flatten(), Theta.flatten()] # np.r_函数对于1维数据,进行的就是合并的操作,和np.append作用相同,但是高维度就是行相加
pass2.4 解序列
上面合并成了一维数据,但在运算时候还是需要用到矩阵的四和运算,因为合并时候是电影在前用户在后,所以前(电影数量*特征数量)个数据是属于X矩阵的,剩下的为Theta矩阵
# 恢复参数形状
def recover_shape(coverage_XTheta, num_users, num_movies, num_features):
X = coverage_XTheta[: num_movies * num_features].reshape(num_movies, num_features)
Theta = coverage_XTheta[num_movies * num_features:].reshape(num_users, num_features)
return X, Theta
pass2.5 代价函数
代价函数的公式如下,给定X求Theta的代价函数,给点Theta求X的代价函数,将他们结合
下面为结合之后的公式,俩项正则项,分别是X和Theta矩阵,其他地方相同
下面是我用矩阵来进行求解的过程
求出预测矩阵带入公式即可,因为只检测有评分的电影,所以最后直接与矩阵R进行点乘即可
# 代价函数
def cost_function(coverage_XTheta, num_users, num_movies, num_features, Y, R, lamda):
X1, Theta1 = recover_shape(coverage_XTheta, num_users, num_movies, num_features)
variance_part = np.power((X1 @ Theta1.T - Y) * R, 2).sum() # [email protected]为所有预测的值偏差,与矩阵R进行点成,筛选出看过的电影
reg1 = lamda * np.power(X1, 2).sum()
reg2 = lamda * np.power(Theta1, 2).sum()
return (variance_part + reg1 + reg2) * (1 / 2)
pass随便取些值看一下代价函数
users = 4
movies = 5
features = 2
X1 = X[:movies,:features]
theta1 = Theta[:users,:features]
coverage_1 = change_shape(X1,theta1)
Y1 = Y[:movies,:users]
R1 = R[:movies,:users]
print(cost_function(coverage_1,users,movies,features,Y1,R1,1))2.6 梯度下降导数部分
这里只需要提供梯度下降的导数即可,opt.minimize()函数会用内部算法自动进行迭代更新
矩阵求法的推导过程与上面相似,有很多写的形式都可以,在Theta导数部分也可以将转质放到后面一起翻转,只要结构和结果对怎么都可以
# 下面是梯度下降的导数参数
def gradient_func(coverage_XTheta, num_users, num_movies, num_features, Y, R, lamda):
X1, Theta1 = recover_shape(coverage_XTheta, num_users, num_movies, num_features)
X_derivative = ((X @ Theta1.T - Y) * R) @ Theta1 + lamda * X1
Theta_derivative = ((Theta1 @ X.T - Y.T) * R.T) @ X + lamda * Theta1
return change_shape(X_derivative, Theta_derivative)
pass2.7 添加新用户
# 添加新的用户
my_ratings = np.zeros((num_movies, 1))
my_ratings[0] = 5
my_ratings[7] = 5
my_ratings[14] = 4
my_ratings[21] = 4
my_ratings[28] = 3
my_ratings[35] = 3
my_ratings[75] = 2
my_ratings[163] = 2
my_ratings[260] = 1
my_ratings[370] = 5
my_ratings[580] = 5
my_ratings[600] = 5
my_ratings[800] = 5
# print(Y.shape,R.shape)
Y = np.c_[Y, my_ratings]
R = np.c_[R, my_ratings != 0]
# print(Y.shape,R.shape)添加一个新用户之后,Y矩阵与R矩阵的维度如下,列增加1
2.8 进行均值归一化
# 均值归一化
def formulization(Y, R):
Y_mean = Y.sum(1) / R.sum(1)
Y_formu = (Y - Y_mean.reshape(Y.shape[0], 1)) * R
return Y_formu,Y_mean
pass2.9 初始化数据
这里np.random.random()是指随机初始化0-1之间的小数
Y_formu,Y_mean = formulization(Y, R)
num_movies, num_users = Y_formu.shape
num_features = 10
X = np.random.random((num_movies, num_features))
Theta = np.random.random((num_users, num_features))
# print(X.shape, Theta.shape) # (1682, 10) (944, 10)
converage_XTheta = change_shape(X, Theta)
lamda = 10下面进行计算X,Theta
res = minimize(fun=cost_function, x0=converage_XTheta, args=(num_users, num_movies, num_features, Y_formu, R, lamda),
method='TNC', jac=gradient_func, options={'maxiter': 100})
X_res, Theta_res = recover_shape(res.x, num_users, num_movies, num_features)
print(X_res,Theta_res)3.0 预测新用户未看过的电影评分
预测评分矩阵公式还是X @ Theta.T,要注意的是这里需要重新加上算出的Y每行的平均值,因为在归一化操作时被减掉了
还要注意的是np.argsort()这个函数是将矩阵从小到大排列,并返回排好序的元素下标,这里添加个负号,矩阵里面最大的元素就会变成最小的元素,去掉负号之后返回的坐标就是从大到小的数了,简单来说就是获得了从大到小的序列
之后我们取10个预测评分最高的电影序号
# 下面开始预测
prediction_matrix = X_res @ Theta_res.T + Y_mean.reshape(num_movies,1)
last_user = prediction_matrix[:,-1]
sort_list = np.argsort(-last_user)
top_ten = sort_list[:10]3.1 导入电影名字
# 导入电影名字
movies = [] # 包含所有电影的列表
with open('movie_ids.txt','r', encoding='latin 1') as f:
for line in f:
# movies.append(' '.join(line.strip().split(' ')[1:]))
movies.append(' '.join(line.strip().split(' ')[1:]))
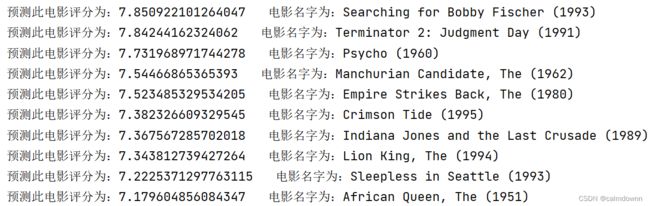
取出推荐的10部电影
for i in top_ten:
print(f"预测此电影评分为:{last_user[i]} 电影名字为:{movies[i]}")四. 全部代码
1.异常检测代码
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.io import loadmat
data = loadmat('ex8data1.mat')
# print(data.keys()) # ['__header__', '__version__', '__globals__', 'X', 'Xval', 'yval']
Xtest = data['X']
Xval = data['Xval']
yval = data['yval']
# print(Xtest.shape,Xval.shape,yval.shape) # (307, 2) (307, 2) (307, 1)
# 看一下图像分布
def plot_pic(Xtest):
plt.figure(figsize=(13, 8))
plt.scatter(Xtest[:, 0], Xtest[:, 1], c='purple', s=150)
pass
# plot_pic(Xtest)
# plt.show()
# 获取一下高斯函数的参数
def get_gaussian_parameters(Xtest):
X_rows, X_colums = Xtest.shape
mean_matrix = Xtest.sum(0) * (1 / X_rows) # sum0是列求和,sum1是行求和,这里得到的是每个特征值的平均值mu
variance_matrix = np.power(Xtest - mean_matrix, 2).sum(0) * (1 / X_rows) # 里面存放每个特征值的方差
return mean_matrix, variance_matrix
pass
# mean_matrix,variance_matrix = get_gaussian_parameters(Xtest)
# print(mean_matrix,variance_matrix)
# 高斯函数
def get_gaussian(mean_matrix, variance_matrix, Xtest):
X_rows, X_colums = Xtest.shape
front = np.power(2 * np.pi * np.power(variance_matrix, 1 / 2), 1 / 2 * (-1)) # 公式前一部分
back = np.exp(-np.power(Xtest - mean_matrix, 2) / (2 * variance_matrix)) # 公式后一部分
p = front * back
p_matrix = np.prod(p, axis=1) # 得到一个1*307的矩阵,每一列都是已经算好的,根据公式累乘就行
return p_matrix
pass
# mean_matrix,variance_matrix = get_gaussian_parameters(Xtest)
# p_matrix = get_gaussian(mean_matrix,variance_matrix,Xtest)
# print(p_matrix)
# print(p_matrix.shape)
# 画一下高等线图
def plot_countour(mean_matrix, variance_matrix, Xtest):
plt.figure(figsize=(13, 8))
x = np.linspace(0, 30, 100)
y = np.linspace(0, 30, 100)
xx, yy = np.meshgrid(x, y) # 将xy绘制成网格,xx,yy分别是网格的所有横纵坐标
zz = np.c_[xx.ravel(), yy.ravel()] # 将网格中每一个小网格的坐标都放入z中,然后进行高斯函数求值(10000,2)
p = get_gaussian(mean_matrix, variance_matrix, zz) # 高斯函数返回的是(10000,)维度的矩阵
p = p.reshape(xx.shape) # 重新绘制成网格的形态(100,100)
cont_levels = [10 ** h for h in range(-20, 0, 3)]
plt.contour(xx, yy, p, cont_levels) # xx,yy代表的是底部平面,平面由网格组成,每个网格的值也就是P值,就是高度,高度越高代表概率越大
plt.scatter(Xtest[:, 0], Xtest[:, 1], c='purple', s=100)
pass
# mean_matrix,variance_matrix = get_gaussian_parameters(Xtest)
# plot_countour(mean_matrix,variance_matrix,Xtest)
# plt.show()
# 下面构造一个评分函数,判断边界函数是否够好
def predict_score(p, yval, e):
p = p.reshape(yval.shape)
rows, columns = yval.shape
TP = 0
FP = 0
TN = 0
FN = 0
prec = 0
rec = 0
F1 = 0
# p ( x ) < ε 被认为异常(y = 1),p ( x ) < ε(y = 0) 被认为正常
for i in range(rows):
if (p[i, :] > e): # 预测为0
if (yval[i, :] == 0):
TN += 1 # 实际为0
else:
FN += 1 # 实际为1
if (p[i, :] < e): # 预测为1
if (yval[i, :] == 1):
TP += 1 # 实际为1
else:
FP += 1 # 实际为0
if (TP + FP):
prec = TP / (TP + FP)
if (TP + FN):
rec = TP / (TP + FN)
if (prec + rec):
F1 = (2 * prec * rec) / (prec + rec)
return F1
pass
# mean_matrix,variance_matrix = get_gaussian_parameters(Xtest)
# p_matrix = get_gaussian(mean_matrix,variance_matrix,Xval)
# F1 = predict_score(p_matrix,yval,p_matrix[0])
# 下面构造select函数,用来选出最好的ε作为分解条件
def select_beste(p, yval):
p_max = np.max(p)
p_min = np.min(p)
e_list = np.linspace(p_min, p_max, 1000)
best_score = 0
final_e = p_min
for i in e_list:
cur_score = predict_score(p, yval, i)
if (cur_score > best_score):
best_score = cur_score
final_e = i
return best_score, final_e
# # 图上找出异常点
# def find_weird(p,final_e,Xtest):
# weird_point = []
# for i in range(len(p)):
# if (p[i] < final_e):
# weird_point.append(Xtest[i,:])
# return weird_point
# pass
# 取一下边界e
# mean_matrix, variance_matrix = get_gaussian_parameters(Xtest)
# p_matrix = get_gaussian(mean_matrix, variance_matrix, Xval)
# best_score, final_e = select_beste(p_matrix, yval)
# print(f"best_score:{best_score},final_e:{final_e}")
# # ---------------------------------------------------------------
# p_matrix1 = get_gaussian(mean_matrix,variance_matrix,Xtest) # 这个p矩阵一定要是Xtest的
# weird_point = np.where(p_matrix1 < final_e)[0]
# plot_countour(mean_matrix,variance_matrix,Xtest)
# plt.scatter(Xtest[weird_point,0],Xtest[weird_point,1],edgecolors='r',s=300,facecolors='none')
# plt.show()
# -----------------------------------------------------------------------
# 数据集ex7data2.mat
data2 = loadmat('ex8data2.mat')
# print(data2.keys()) # ['__header__', '__version__', '__globals__', 'X', 'Xval', 'yval']
X2test = data2['X']
X2val = data2['Xval']
y2val = data2['yval']
# print(X2test.shape, X2val.shape, yval.shape) # (1000, 11) (100, 11) (100, 1)
mean_matrix, variance_matrix = get_gaussian_parameters(X2test)
p_matrix = get_gaussian(mean_matrix, variance_matrix, X2val)
best_score, final_e = select_beste(p_matrix, y2val)
print(f"best_score:{best_score},final_e:{final_e}")
p_matrix1 = get_gaussian(mean_matrix,variance_matrix,X2test)
weird_point = np.where(p_matrix1 < final_e)[0]
print(len(weird_point))
2.推荐系统代码
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.io import loadmat
from scipy.optimize import minimize
data = loadmat('ex8_movies.mat')
# print(data.keys()) # ['__header__', '__version__', '__globals__', 'Y', 'R']
Y = data['Y'] # 不用用户对于不同电影的评分,行为电影数,列为用户数(维度:1682,943)
R = data['R'] # 判断是否有评分,维度与Y矩阵相同
# print(Y.shape,R.shape)
data2 = loadmat('ex8_movieParams.mat')
# print(data2.keys()) # ['__header__', '__version__', '__globals__', 'X', 'Theta', 'num_users', 'num_movies', 'num_features']
X = data2['X'] # 电影类型偏向的特征值
Theta = data2['Theta'] # 用户的特征值
num_users = int(data2['num_users']) # 用户数量
num_movies = int(data2['num_movies']) # 电影数量
num_features = int(data2['num_features']) # 特征数量(X和Theta矩阵的)
# print(X.shape,Theta.shape) # (1682, 10) (943, 10)
# print(num_users,num_movies,num_features) # [943] [1682] [10]
# 更改参数形状
def change_shape(X, Theta):
return np.r_[X.flatten(), Theta.flatten()] # np.r_函数对于1维数据,进行的就是合并的操作,和np.append作用相同,但是高维度就是行相加
pass
# print(change_shape(X,Theta).shape)
# 恢复参数形状
def recover_shape(coverage_XTheta, num_users, num_movies, num_features):
X = coverage_XTheta[: num_movies * num_features].reshape(num_movies, num_features)
Theta = coverage_XTheta[num_movies * num_features:].reshape(num_users, num_features)
return X, Theta
pass
# coverage_XTheta = change_shape(X,Theta)
# X1,Theta1 = recover_shape(coverage_XTheta,num_users,num_movies,num_features)
# print(X1.shape,Theta1.shape)
# 代价函数
def cost_function(coverage_XTheta, num_users, num_movies, num_features, Y, R, lamda):
X1, Theta1 = recover_shape(coverage_XTheta, num_users, num_movies, num_features)
variance_part = np.power((X1 @ Theta1.T - Y) * R, 2).sum() # [email protected]为所有预测的值偏差,与矩阵R进行点成,筛选出看过的电影
reg1 = lamda * np.power(X1, 2).sum()
reg2 = lamda * np.power(Theta1, 2).sum()
return (variance_part + reg1 + reg2) * (1 / 2)
pass
# users = 4
# movies = 5
# features = 2
# X1 = X[:movies,:features]
# theta1 = Theta[:users,:features]
# coverage_1 = change_shape(X1,theta1)
# Y1 = Y[:movies,:users]
# R1 = R[:movies,:users]
# print(cost_function(coverage_1,users,movies,features,Y1,R1,1))
# 下面是梯度下降的导数参数
def gradient_func(coverage_XTheta, num_users, num_movies, num_features, Y, R, lamda):
X1, Theta1 = recover_shape(coverage_XTheta, num_users, num_movies, num_features)
X_derivative = ((X @ Theta1.T - Y) * R) @ Theta1 + lamda * X1
Theta_derivative = ((Theta1 @ X.T - Y.T) * R.T) @ X + lamda * Theta1
return change_shape(X_derivative, Theta_derivative)
pass
# test1 = gradient_func(change_shape(X,Theta),num_users,num_movies,num_features,Y,R,1)
# print(test1)
# 添加新的用户
my_ratings = np.zeros((num_movies, 1))
my_ratings[0] = 5
my_ratings[7] = 5
my_ratings[14] = 4
my_ratings[21] = 4
my_ratings[28] = 3
my_ratings[35] = 3
my_ratings[75] = 2
my_ratings[163] = 2
my_ratings[260] = 1
my_ratings[370] = 5
my_ratings[580] = 5
my_ratings[600] = 5
my_ratings[800] = 5
# print(Y.shape,R.shape)
Y = np.c_[Y, my_ratings]
R = np.c_[R, my_ratings != 0]
# print(Y.shape,R.shape)
# 均值归一化
def formulization(Y, R):
Y_mean = Y.sum(1) / R.sum(1)
Y_formu = (Y - Y_mean.reshape(Y.shape[0], 1)) * R
return Y_formu,Y_mean
pass
Y_formu,Y_mean = formulization(Y, R)
num_movies, num_users = Y_formu.shape
num_features = 10
X = np.random.random((num_movies, num_features))
Theta = np.random.random((num_users, num_features))
# print(X.shape, Theta.shape) # (1682, 10) (944, 10)
converage_XTheta = change_shape(X, Theta)
lamda = 10
#
res = minimize(fun=cost_function, x0=converage_XTheta, args=(num_users, num_movies, num_features, Y_formu, R, lamda),
method='TNC', jac=gradient_func, options={'maxiter': 100})
X_res, Theta_res = recover_shape(res.x, num_users, num_movies, num_features)
# print(X_res,Theta_res)
#
# 下面开始预测
prediction_matrix = X_res @ Theta_res.T + Y_mean.reshape(num_movies,1)
last_user = prediction_matrix[:,-1]
sort_list = np.argsort(-last_user)
top_ten = sort_list[:10]
#
# 导入电影名字
movies = [] # 包含所有电影的列表
with open('movie_ids.txt','r', encoding='latin 1') as f:
for line in f:
movies.append(' '.join(line.strip().split(' ')[1:]))
for i in top_ten:
print(f"预测此电影评分为:{last_user[i]} 电影名字为:{movies[i]}")