Chapter9.4:状态反馈与极点配置
该系列博客主要讲述Matlab软件在自动控制方面的应用,如无自动控制理论基础,请先学习自动控制系列博文,该系列博客不再详细讲解自动控制理论知识。
自动控制理论基础相关链接:https://blog.csdn.net/qq_39032096/category_10287468.html?spm=1001.2014.3001.5482
博客参考书籍:《MATLAB/Simulink与控制系统仿真》。
4.状态反馈与极点配置
4.1 线性定常系统常用反馈结构及其对系统特性的影响
4.1.1 状态反馈和输出反馈
-
状态反馈
设有 n n n维线性定常系统:
x ˙ = A x + B u , y = C x \dot{x}=Ax+Bu,y=Cx x˙=Ax+Bu,y=Cx
式中: x 、 u 、 y x、u、y x、u、y分别为 n n n维、 p p p维和 q q q维向量; A 、 B 、 C A、B、C A、B、C分别为 n × n 、 n × p 、 q × n n\times{n}、n\times{p}、q\times{n} n×n、n×p、q×n实数矩阵;当将系统的控制量 u u u取为状态变量的线性函数:
u = v − K x u=v-Kx u=v−Kx
称为线性直接状态反馈,简称状态反馈,其中 v v v为 p p p维参考输入向量, K K K为 ( p × n ) (p\times{n}) (p×n)维实反馈增益矩阵;整理化简可得状态反馈系统动态方程:
x ˙ = ( A − B K ) x + B v , y = C x \dot{x}=(A-BK)x+Bv,y=Cx x˙=(A−BK)x+Bv,y=Cx
其传递函数矩阵为:
G K ( s ) = C ( s I − A + B K ) − 1 B G_{K}(s)=C(sI-A+BK)^{-1}B GK(s)=C(sI−A+BK)−1B
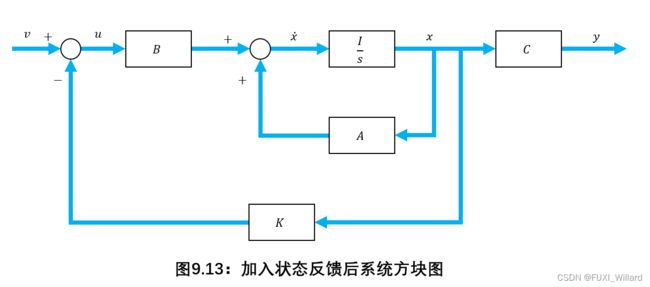
加入状态反馈后系统方块图如下图所示: -
输出反馈
输出反馈的目的:使系统闭环成为稳定系统,然后在此基础上进一步改善闭环系统性能;
输出反馈的两种形式:一种是将输出量反馈至状态微分,另一种是将输出量反馈至参考输入;
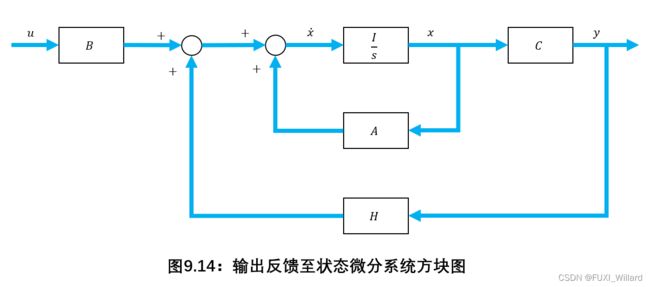
输出量反馈至状态微分系统方块图如下图所示:
输出反馈系统的动态方程为:
x ˙ = A x + B u − H y = ( A − H C ) x + B u , y = C x \dot{x}=Ax+Bu-Hy=(A-HC)x+Bu,y=Cx x˙=Ax+Bu−Hy=(A−HC)x+Bu,y=Cx
其传递矩阵为:
G H ( s ) = C ( s I − A + H C ) − 1 B G_H(s)=C(sI-A+HC)^{-1}B GH(s)=C(sI−A+HC)−1B
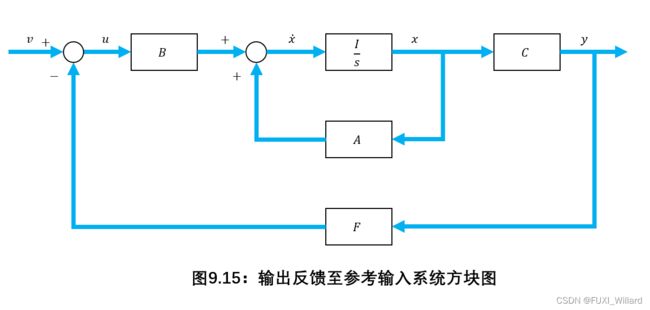
将输出量反馈至输入系统方块图如下图所示:当将系统的控制量 u u u取为输出 y y y的线性函数:
u = v − F y u=v-Fy u=v−Fy
称为线性非动态输出反馈,简称输出反馈,其中 v v v为 p p p维参考输入向量, F F F为 p × q p\times{q} p×q维实反馈增益矩阵,是一种最常用的输出反馈;输出反馈系统动态方程:
x ˙ = ( A − B F C ) x + B v , y = C x \dot{x}=(A-BFC)x+Bv,y=Cx x˙=(A−BFC)x+Bv,y=Cx
其传递函数矩阵为:
G F ( s ) = C ( s I − A + B F C ) − 1 B G_F(s)=C(sI-A+BFC)^{-1}B GF(s)=C(sI−A+BFC)−1B
利用状态反馈时,其信息量大而完整,可以在不增加系统维数的情况下,自由地支配响应特性;输出反馈仅利用状态变量的线性组合进行反馈,其信息量较小,所引入的补偿装置将使系统维数增加,且难以得到任意的所期望的响应特性;
4.1.2 反馈结构对系统性能的影响
-
对系统可控性和可观测性的影响
定理1:对于线性定常系统,状态反馈的引入不改变系统的可控性,但可能改变系统的可观测性;
状态反馈可能改变系统的可观测性,其原因是状态反馈造成了所配置的极点与零点相对消;
定理2:对于线性定常系统,输出至状态微分反馈的引入不改变的可观测性,但可能改变系统的可控性;
定理3:对于线性定常系统,输出至参考输入反馈的引入能同时不改变系统的可控性和可观测性,即输出反馈系统 Σ F \Sigma_F ΣF为可控(可观测)的充分必要条件是被控系统 Σ 0 \Sigma_0 Σ0为可控(可观测);
-
对系统稳定性的影响
状态反馈和输出反馈都能影响系统的稳定性,加入反馈,使得通过反馈构成的闭环系统成为稳定系统,称之为镇定;
对于线性定常被控系统:
x ˙ = A x + B u \dot{x}=Ax+Bu x˙=Ax+Bu
如果可以找到状态反馈控制律:
u = − K x + v u=-Kx+v u=−Kx+v
其中: v v v为参考输入,使得通过反馈构成的闭环系统:
x ˙ = ( A − B K ) x + B v \dot{x}=(A-BK)x+Bv x˙=(A−BK)x+Bv
是渐近稳定的,即 ( A − B K ) (A-BK) (A−BK)的特征值均具有负实部,则称系统实现了状态反馈镇定;定理4:当且仅当线性定常系统的不可控部分渐近稳定时,系统是状态反馈可镇定的;
4.2 系统的极点配置
状态反馈和输出反馈都能改变闭环系统的极点位置;极点配置:利用状态反馈或输出反馈使闭环系统的极点位于所希望的极点位置;
-
极点可配置条件
-
利用状态反馈的极点可配置条件
定理5:利用状态反馈任意配置闭环极点的充分必要条件是被控线性定常系统可控。
-
利用输出反馈的极点可配置条件
定理6:用输出至状态微分的反馈任意配置闭环极点的充分必要条件是被控线性定常系统可观测;
-
-
单输入-单输出系统的极点配置算法
配置步骤:
-
列写系统状态方程及状态反馈控制律
x ˙ = A x + b u , u = v − k x \dot{x}=Ax+bu,u=v-kx x˙=Ax+bu,u=v−kx
其中: k = [ k 0 k 1 ⋯ k n − 1 ] k=\begin{bmatrix}k_0 & k_1 & \cdots & k_{n-1}\end{bmatrix} k=[k0k1⋯kn−1]; -
检验 ( A , b ) (A,b) (A,b)的可控性,若 r a n k [ b A b ⋯ A n − 1 b ] = n {\rm rank}\begin{bmatrix}b & Ab & \cdots & A^{n-1}b\end{bmatrix}=n rank[bAb⋯An−1b]=n,则转下一步;
-
由要求配置的闭环极点 λ 1 , λ 2 , ⋯ , λ n \lambda_1,\lambda_2,\cdots,\lambda_n λ1,λ2,⋯,λn,求出希望特征多项式 a 0 ∗ ( s ) = ∏ i = 1 n ( s − λ i ) a_0^*(s)=\displaystyle\prod_{i=1}^{n}(s-\lambda_i) a0∗(s)=i=1∏n(s−λi);
-
计算状态反馈系统的特征多项式 a 0 ( s ) = det [ s I − A + b k ] a_0(s)=\det[sI-A+bk] a0(s)=det[sI−A+bk];
-
比较多项式 a 0 ( s ) a_0(s) a0(s)与 a 0 ∗ ( s ) a_0^*(s) a0∗(s),令其对应项系数相等,可确定状态反馈增益向量 k k k;
应用极点配置方法来改善系统性能需要注意的:
- 配置极点时并非离虚轴越远越好,以免造成系统带宽过大使抗干扰性降低;
- 状态反馈向量 k k k中的元素不宜过大,否则物理实现不易;
- 闭环零点对系统动态性能影响甚大,在规定希望配置的闭环极点时,需要充分考虑闭环零点的影响;
- 状态反馈对系统的零点和可观测性没有影响,只有当任意配置的极点与系统零点存在对消时,状态反馈系统的零点和可观测性将会发生改变;
- 以上几点适用于单输入-多输出或单输出系统,不适用于多输入-多输出系统;
实例分析:
Example1: 已知单输入线性定常系统的状态方程为:
x ˙ = [ 0 0 0 1 − 6 0 0 1 − 12 ] x + [ 1 0 0 ] u \dot{x}= \begin{bmatrix} 0 & 0 & 0\\ 1 & -6 & 0\\ 0 & 1 & -12 \end{bmatrix}x+ \begin{bmatrix} 1\\ 0\\ 0 \end{bmatrix}u x˙= 0100−6100−12 x+ 100 u
求状态反馈向量 k k k,使系统的闭环特征值为:
λ 1 = − 2 , λ 2 = − 1 + j , λ 3 = − 1 − j \lambda_1=-2,\lambda_2=-1+{\rm j},\lambda_3=-1-{\rm j} λ1=−2,λ2=−1+j,λ3=−1−j
解:系统的可控性判别矩阵为:
S c = [ b A b A 2 b ] = [ 1 0 0 0 1 − 6 0 0 1 ] S_c= \begin{bmatrix} b & Ab & A^2b \end{bmatrix}= \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & -6\\ 0 & 0 & 1 \end{bmatrix} Sc=[bAbA2b]= 1000100−61 r a n k S c = 3 = n {\rm rank}S_c=3=n rankSc=3=n
故系统可控,满足极点可配置条件.
系统的特征多项式为:
det ( s I − A ) = det [ s 0 0 − 1 s + 6 0 0 − 1 s + 12 ] = s 3 + 18 s 2 + 72 s \det(sI-A)= \det\begin{bmatrix} s & 0 & 0\\ -1 & s+6 & 0\\ 0 & -1 & s+12 \end{bmatrix}=s^3+18s^2+72s det(sI−A)=det s−100s+6−100s+12 =s3+18s2+72s
希望特征多项式为:
a 0 ∗ ( s ) = ( s − λ 1 ) ( s − λ 2 ) ( s − λ 3 ) = ( s + 2 ) ( s + 1 − j ) ( s + 1 + j ) = s 3 + 4 s 2 + 6 s + 4 a_0^*(s)=(s-\lambda_1)(s-\lambda_2)(s-\lambda_3)=(s+2)(s+1-{\rm j})(s+1+{\rm j})=s^3+4s^2+6s+4 a0∗(s)=(s−λ1)(s−λ2)(s−λ3)=(s+2)(s+1−j)(s+1+j)=s3+4s2+6s+4
可求得:
k ‾ = [ a 0 ∗ − a 0 a 1 ∗ − a 1 a 2 ∗ − a 2 ] = [ 4 − 66 − 14 ] \overline{k}= \begin{bmatrix} a^*_0-a_0 & a^*_1-a_1 & a^*_2-a_2 \end{bmatrix}= \begin{bmatrix} 4 & -66 & -14 \end{bmatrix} k=[a0∗−a0a1∗−a1a2∗−a2]=[4−66−14]变换矩阵为:
P − 1 = [ A 2 b A b b ] [ 1 0 0 a 2 1 0 a 1 a 2 1 ] = [ 1 0 0 − 6 1 0 1 0 0 ] [ 1 0 0 18 1 0 72 18 1 ] = [ 72 18 1 12 1 0 1 0 0 ] P^{-1}= \begin{bmatrix} A^2b & Ab & b \end{bmatrix} \begin{bmatrix} 1 & 0 & 0\\ a_2 & 1 & 0\\ a_1 & a_2 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0\\ -6 & 1 & 0\\ 1 & 0 & 0 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0\\ 18 & 1 & 0\\ 72 & 18 & 1 \end{bmatrix}= \begin{bmatrix} 72 & 18 & 1\\ 12 & 1 & 0\\ 1 & 0 & 0 \end{bmatrix} P−1=[A2bAbb] 1a2a101a2001 = 1−61010000 118720118001 = 721211810100
P = [ 0 0 1 0 1 − 12 1 − 18 144 ] P= \begin{bmatrix} 0 & 0 & 1\\ 0 & 1 & -12\\ 1 & -18 & 144 \end{bmatrix} P= 00101−181−12144
k = k ‾ P = [ 4 − 66 − 14 ] [ 0 0 1 0 1 − 12 1 − 18 144 ] = [ − 14 186 − 1220 ] k=\overline{k}P= \begin{bmatrix} 4 & -66 & -14 \end{bmatrix} \begin{bmatrix} 0 & 0 & 1\\ 0 & 1 & -12\\ 1 & -18 & 144 \end{bmatrix}= \begin{bmatrix} -14 & 186 & -1220 \end{bmatrix} k=kP=[4−66−14] 00101−181−12144 =[−14186−1220]
或
a 0 ∗ ( s ) = det ( s I − A + b k ) = [ s + k 1 k 2 k 3 − 1 s + 6 0 0 − 1 s + 12 ] = s 3 + ( k 1 + 18 ) s 2 + ( 18 k 1 + k 2 + 72 ) s + ( 72 k 1 + 12 k 2 + k 3 ) \begin{aligned} a^*_0(s)&=\det(sI-A+bk)\\\\ &=\begin{bmatrix}s+k_1 & k_2 & k_3\\ -1 & s+6 & 0\\ 0 & -1 & s+12 \end{bmatrix}\\\\ &=s^3+(k_1+18)s^2+(18k_1+k_2+72)s+(72k_1+12k_2+k_3) \end{aligned} a0∗(s)=det(sI−A+bk)= s+k1−10k2s+6−1k30s+12 =s3+(k1+18)s2+(18k1+k2+72)s+(72k1+12k2+k3){ k 1 + 18 = 4 18 k 1 + k 2 + 72 = 6 72 k 1 + 12 k 2 + k 3 = 4 \begin{cases} &k_1+18=4\\ &18k_1+k_2+72=6\\ &72k_1+12k_2+k_3=4 \end{cases} ⎩ ⎨ ⎧k1+18=418k1+k2+72=672k1+12k2+k3=4
求得:
k 1 = − 14 , k 2 = 186 , k 3 = − 1220 k_1=-14,k_2=186,k_3=-1220 k1=−14,k2=186,k3=−1220
可得:
k = [ k 1 k 2 k 3 ] = [ − 14 186 − 1220 ] k= \begin{bmatrix} k_1 & k_2 & k_3 \end{bmatrix}= \begin{bmatrix} -14 & 186 & -1220 \end{bmatrix} k=[k1k2k3]=[−14186−1220] -
-
状态反馈对传递函数零点的影响
状态反馈对 G ( s ) G(s) G(s)的零点没有影响,仅使 G ( s ) G(s) G(s)的极点改变为闭环系统极点,但可能引入状态反馈后恰巧使某些极点移到 G ( s ) G(s) G(s)的零点处而构成极、零点对消,这时既失去了一个系统零点,又失去了一个系统极点,且被对消掉的那些极点可能不可观测;
4.3 MATLAB/SIMULINK在极点配置中的应用
4.3.1 极点配置常用函数
-
p l a c e ( ) {\rm place()} place()函数。
-
p l a c e ( ) {\rm place()} place()函数是基于鲁棒极点配置的算法编写的,用来求取状态反馈阵 K K K,使得多输入系统具有指定的闭环极点 p p p,即 p = e i g ( A − B ⋅ K ) p={\rm eig}(A-B\cdot{K}) p=eig(A−B⋅K);
-
常用调用格式:
# 语法格式: K=place(A,B,p) [K,prec,message]=place(A,B,p) # 参数说明: (A,B):系统状态方程模型; p:包含期望闭环极点位置的列向量; K:状态反馈行向量; prec:闭环系统的实际极点与期望极点p的接近程度,prec的每个量的值为匹配的位数; # 注1:如果闭环系统的实际极点偏离期望极点10%以上,message将给出警告信息; # 注2:函数place()不适用于含有多重期望极点的配置问题;
-
-
a c k e r ( ) {\rm acker()} acker()函数。
-
a c k e r ( ) {\rm acker()} acker()函数是根据 A c k e r m a n {\rm Ackerman} Ackerman公式编写;
-
常用调用格式:
# 语法格式: K=acker(A,B,p) # 参数说明: (A,B):系统状态方程模型; p:包含期望闭环极点位置的列向量; K:状态反馈行向量; # 注:acker()只适用于单输入系统,希望的极点可以包括多重极点;
-
4.3.2 实战1
实验要求:已知控制系统的方程为: X = A X + B U X=AX+BU X=AX+BU,其中:
A = [ 0 1 0 0 0 1 − 1 − 5 − 6 ] , B = [ 0 0 1 ] A=\begin{bmatrix} 0 & 1 & 0\\ 0 & 0 & 1\\ -1 & -5 & -6 \end{bmatrix},B=\begin{bmatrix} 0\\0\\1 \end{bmatrix} A= 00−110−501−6 ,B= 001
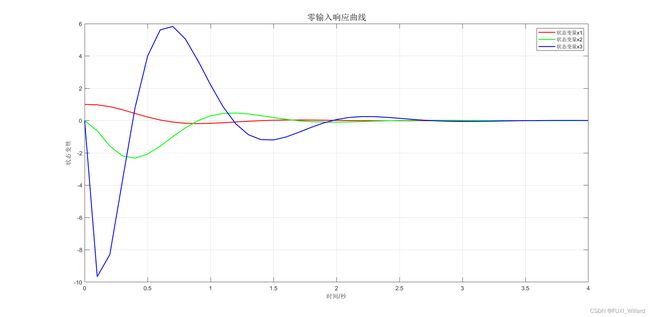
采用状态反馈: U = − K X U=-KX U=−KX,希望的闭环极点为: p 1 , 2 = − 2 ± j 4 , p 3 = − 10 p_{1,2}=-2±{\rm j}4,p_3=-10 p1,2=−2±j4,p3=−10,使用 M A T L A B {\rm MATLAB} MATLAB确定状态反馈增益矩阵,计算当系统初始条件为: X 0 = [ 1 , 0 , 0 ] {X_0=\begin{bmatrix}1,0,0\end{bmatrix}} X0=[1,0,0]时的零输入响应。
解:
% 实例Chapter9.4.3.2
clc;clear;
A=[0,1,0;0,0,1;-1,-5,-6];B=[0;0;1]; % 状态矩阵和输入矩阵
P=[-2+1i*4,-2-1i*4,-10]; % 期望的闭环极点
K=acker(A,B,P) % 极点配置
sys=ss(A-B*K,eye(3),eye(3),eye(3)) % 极点配置后的系统
t=0:0.1:4;
X=initial(sys,[1;0;0],t); % 零输入响应
x1=[1,0,0]*X'; % 状态x1
x2=[0,1,0]*X'; % 状态x2
x3=[0,0,1]*X'; % 状态x3
plot(t,x1,'r',t,x2,'g',t,x3,'b');grid;
xlabel('时间/秒');ylabel('状态变量');
legend('状态变量x1','状态变量x2','状态变量x3');
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('零输入响应曲线','FontSize',15);
% 结果显示:
% 状态反馈增益矩阵
K =
199 55 8
% 极点配置后的系统
sys =
A =
x1 x2 x3
x1 0 1 0
x2 0 0 1
x3 -200 -60 -14
B =
u1 u2 u3
x1 1 0 0
x2 0 1 0
x3 0 0 1
C =
x1 x2 x3
y1 1 0 0
y2 0 1 0
y3 0 0 1
D =
u1 u2 u3
y1 1 0 0
y2 0 1 0
y3 0 0 1
4.3.3 实战2
实验要求:已知数字控制系统的状态方程为:
x ( k + 1 ) = [ 0 1 − 0.16 − 1 ] x ( k ) + [ 0 1 ] u ( k ) x(k+1)=\begin{bmatrix} 0 & 1\\ -0.16 & -1 \end{bmatrix}x(k)+\begin{bmatrix} 0\\1 \end{bmatrix}u(k) x(k+1)=[0−0.161−1]x(k)+[01]u(k)
设系统期望的闭环极点为: z = 0.5 ± j 0.5 z=0.5±{\rm j}0.5 z=0.5±j0.5,现用全状态反馈控制系统,求反馈增益矩阵 K K K。
解:
% 实例Chapter9.4.3.3
clc;clear;
A=[0,1;-0.16,-1];B=[0;1];
P=[0.5+1i*0.5,0.5-1i*0.5];
K=acker(A,B,P)
% 反馈增益矩阵为:
% K =
% 0.3400 -2.0000
4.4 全维状态观测器及其设计
很多情况下,多数状态变量不易测得或不可能测得,可利用被控对象的输入量和输出量建立状态观测器(亦称状态估计器、状态重构器)来重构状态的问题,当重构状态向量的维数等于被控对象状态向量的维数时,称为全维状态观测器;
-
全维状态观测器构成方案
设被控对象动态方程为:
x ˙ = A x + B u , y = C x \dot{x}=Ax+Bu,y=Cx x˙=Ax+Bu,y=Cx
构造一个动态方程与被控对象动态方程相同且能用计算机实现的模拟被控系统:
x ^ ˙ = A x ^ + B u , y ^ = C x ^ \dot{\hat{x}}=A\hat{x}+Bu,\hat{y}=C\hat{x} x^˙=Ax^+Bu,y^=Cx^
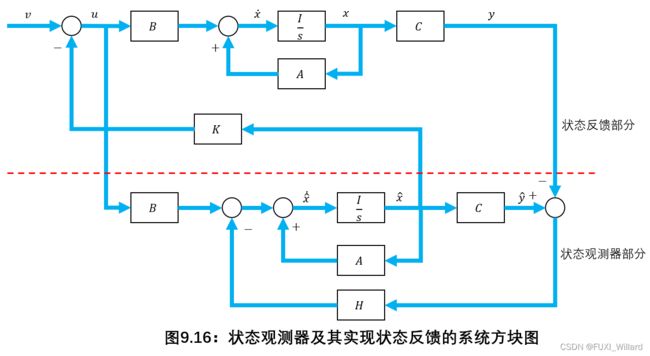
式中: x ^ 、 y ^ \hat{x}、\hat{y} x^、y^分别为模拟系统的状态向量和输出向量,是被控对象状态向量和输出向量的估值;状态观测器有两个输入,即 u u u和 y y y,输出为 x ^ \hat{x} x^,观测器含 n n n个积分器并对全部状态变量做出估计; H H H为观测器输出反馈阵,把 ( y ^ − y ) (\hat{y}-y) (y^−y)负反馈至 x ^ ˙ \dot{\hat{x}} x^˙处,是为配置观测器极点,提高其动态性能,即尽快使 ( x ^ − x ) (\hat{x}-x) (x^−x)逼近于零而引入的;
-
全维状态观测器分析设计
全维状态观测器动态方程:
x ^ ˙ = A x ^ + B u − H ( y ^ − y ) , y ^ = C x ^ \dot{\hat{x}}=A\hat{x}+Bu-H(\hat{y}-y),\hat{y}=C\hat{x} x^˙=Ax^+Bu−H(y^−y),y^=Cx^
故有:
x ^ ˙ = A x ^ + B u − H C ( x ^ − x ) = ( A − H C ) x ^ + B u + H y \dot{\hat{x}}=A\hat{x}+Bu-HC(\hat{x}-x)=(A-HC)\hat{x}+Bu+Hy x^˙=Ax^+Bu−HC(x^−x)=(A−HC)x^+Bu+Hy
式中: ( A − H C ) (A-HC) (A−HC)称为观测器系统矩阵;观测器分析设计的关键问题是能否在任何初始条件下,即尽管 x ^ ( t 0 ) \hat{x}(t_0) x^(t0)与与 x ( t 0 ) x(t_0) x(t0)不同,但总能保证下式成立:
lim t → ∞ ( x ^ ( t ) − x ( t ) ) = 0 \lim_{t\to\infty}(\hat{x}(t)-x(t))=0 t→∞lim(x^(t)−x(t))=0
只有满足上式,状态反馈系统才能正常工作,称为观测器存在条件;定理7:若被控系统 ( A , B , C ) (A,B,C) (A,B,C)可观测,则其状态可用形如
x ^ ˙ = A x ^ + B u − H C ( x ^ − x ) = ( A − H C ) x ^ + B u + H y \dot{\hat{x}}=A\hat{x}+Bu-HC(\hat{x}-x)=(A-HC)\hat{x}+Bu+Hy x^˙=Ax^+Bu−HC(x^−x)=(A−HC)x^+Bu+Hy
的全维状态观测器给出估值,其中矩阵 H H H按任意配置观测器极点的需要来选择,以决定状态误差衰减的速率;实例分析:
Example2: 设被控对象传递函数为:
Y ( s ) U ( s ) = 2 ( s + 1 ) ( s + 2 ) \frac{Y(s)}{U(s)}=\frac{2}{(s+1)(s+2)} U(s)Y(s)=(s+1)(s+2)2
设计全维状态观测器,将极点配置在 − 10 , − 10 -10,-10 −10,−10.解:
被控对象的传递函数为:
Y ( s ) U ( s ) = 2 ( s + 1 ) ( s + 2 ) = 2 s 2 + 3 s + 2 \frac{Y(s)}{U(s)}=\frac{2}{(s+1)(s+2)}=\frac{2}{s^2+3s+2} U(s)Y(s)=(s+1)(s+2)2=s2+3s+22
根据传递函数直接写出系统的可控标准型:
x ˙ = A x + b u , y = c x \dot{x}=Ax+bu,y=cx x˙=Ax+bu,y=cx
其中:
A = [ 0 1 − 2 − 3 ] , b = [ 0 1 ] , c = [ 2 0 ] A= \begin{bmatrix} 0 & 1\\ -2 & -3 \end{bmatrix},b= \begin{bmatrix} 0\\ 1 \end{bmatrix},c= \begin{bmatrix} 2 & 0 \end{bmatrix} A=[0−21−3],b=[01],c=[20]
系统可控可观测, n = 2 , q = 1 n=2,q=1 n=2,q=1,输出反馈向量 h h h为 2 × 1 2\times1 2×1向量.全维状态观测器系统矩阵为:
A − h c = [ 0 1 − 2 − 3 ] − [ h 0 h 1 ] [ 2 0 ] = [ − 2 h 0 1 − 2 − 2 h 1 − 3 ] A-hc= \begin{bmatrix} 0 & 1\\ -2 & -3 \end{bmatrix}- \begin{bmatrix} h_0\\ h_1 \end{bmatrix}\begin{bmatrix} 2 & 0 \end{bmatrix}= \begin{bmatrix} -2h_0 & 1\\ -2-2h_1 & -3 \end{bmatrix} A−hc=[0−21−3]−[h0h1][20]=[−2h0−2−2h11−3]
观测器特征方程为:
∣ λ I − ( A − h c ) ∣ = λ 2 + ( 2 h 0 + 3 ) λ + ( 6 h 0 + 2 h 1 + 2 ) = 0 |\lambda{I}-(A-hc)|=\lambda^2+(2h_0+3)\lambda+(6h_0+2h_1+2)=0 ∣λI−(A−hc)∣=λ2+(2h0+3)λ+(6h0+2h1+2)=0
期望特征方程为:
( λ + 10 ) 2 = λ 2 + 20 λ + 100 = 0 (\lambda+10)^2=\lambda^2+20\lambda+100=0 (λ+10)2=λ2+20λ+100=0
令两特征方程同次项系数相等,可得:
2 h 0 + 3 = 20 , 6 h 0 + 2 h 1 + 2 = 100 2h_0+3=20,6h_0+2h_1+2=100 2h0+3=20,6h0+2h1+2=100
解得:
h 0 = 8.5 , h 1 = 23.5 h_0=8.5,h_1=23.5 h0=8.5,h1=23.5
其中: h 0 , h 1 h_0,h_1 h0,h1分别为 ( y ^ − y ) (\hat{y}-y) (y^−y)引至 x ^ ˙ 1 , x ^ ˙ 2 \dot{\hat{x}}_1,\dot{\hat{x}}_2 x^˙1,x^˙2的反馈系数;被控对象及全维状态观测器组合系统的状态变量图如下图所示:
-
分离特性
定理8(分离定理):若被控系统 ( A , B , C ) (A,B,C) (A,B,C)可控可观测,用状态观测器估值形成状态反馈时,其系统的极点配置和观测器设计可分别独立进行,即 K K K和 H H H阵的设计可分别独立进行;
4.5 MATLAB/SIMULINK在状态观测器设计中的应用
实验要求:给定线性定常系统为: { x ˙ = A x + B u y = C x \begin{cases}&\dot{x}=Ax+Bu\\&y=Cx\end{cases} {x˙=Ax+Buy=Cx,其中:
A = [ 0 1 20.6 0 ] , B = [ 0 1 ] , C = [ 1 0 ] A=\begin{bmatrix} 0 & 1\\ 20.6 & 0 \end{bmatrix},B=\begin{bmatrix} 0\\1 \end{bmatrix},C=\begin{bmatrix} 1 & 0 \end{bmatrix} A=[020.610],B=[01],C=[10]
闭环极点为: s = μ i ( i = 1 , 2 ) s=\mu_i(i=1,2) s=μi(i=1,2),其中: μ 1 = − 1.8 + j 2.4 , μ 1 = − 1.8 − j 2.4 \mu_1=-1.8+{\rm j}2.4,\mu_1=-1.8-{\rm j}2.4 μ1=−1.8+j2.4,μ1=−1.8−j2.4;期望用观测状态反馈控制,而不是用真实的状态反馈控制。观测器的期望特征值为: μ 1 = μ 2 = − 8 \mu_1=\mu_2=-8 μ1=μ2=−8。采用 M A T L A B {\rm MATLAB} MATLAB确定相应的状态反馈增益矩阵 K K K和观测器增益矩阵 K e K_e Ke。
解:
% 实例Chapter9.4.5
clc;clear;
% 判断系统的可控性
A=[0,1;20.6,0];B=[0;1];
C=[1,0];D=[0];
Q=[B,A*B];
rankQ=rank(Q);
if rankQ<2
disp('系统不可控!');
else
disp('系统完全可控!');
end
% 系统完全可控,可实现任意的极点配置
expectPole=[-1.8+1i*2.4,-1.8-1i*2.4]; % 期望的闭环极点
expectPoly1=poly(expectPole) % 期望闭环极点的多项式
Phi=polyvalm(expectPoly1,A);
K=[0,1]*inv(Q)*Phi % 计算状态反馈增益矩阵
% 判断系统的可观性
V=[C',A'*C'];
rankV=rank(V);
if rankV<2
disp('系统不可观!');
else
disp('系统完全可观!');
end
% 系统完全可观,可以对系统设计观测器
expectCharacteristicRoot=[-8,0;0,-8];
expectPoly2=poly(expectCharacteristicRoot)
Ph=polyvalm(expectPoly2,A);
Ke=Ph*(inv(V'))*[0;1] % 计算观测器增益矩阵
% 计算系统特征多项式
X=[eig(A-B*K);eig(A-Ke*C)]; % 计算矩阵的特征值和特征向量的函数
poly(X)
% 结果:
系统完全可控!
expectPoly1 =
1.0000 3.6000 9.0000
K =
29.6000 3.6000
系统完全可观!
expectPoly2 =
1 16 64
Ke =
16.0000
84.6000
ans =
1.0000 19.6000 130.6000 374.4000 576.0000
4.6 综合实例及MATLAB/SIMULINK应用
实验要求:给定一个线性系统,其状态空间表达式为:
{ X ′ = [ 0 1 0 − 5 ] X + [ 0 100 ] u y = [ 1 0 ] X \begin{cases} &X'=\begin{bmatrix} 0 & 1\\ 0 & -5 \end{bmatrix}X+\begin{bmatrix} 0\\100 \end{bmatrix}u\\\\ &y=\begin{bmatrix} 1 & 0 \end{bmatrix}X \end{cases} ⎩ ⎨ ⎧X′=[001−5]X+[0100]uy=[10]X
采用二维状态反馈方法,实现闭环阻尼比 ζ = 0.707 \zeta=0.707 ζ=0.707,无阻尼自然振荡频率 ω c = 10 r a d / s \omega_c=10{\rm rad/s} ωc=10rad/s。
解:
【 S T E P 1 {\rm STEP1} STEP1】:建立控制系统的状态空间模型。
% STEP1:建立控制系统状态空间模型
A=[0,1;0,-5];B=[0;100];
C=[1,0];D=0;
sys=ss(A,B,C,D)
% MATLAB结果:
sys =
A =
x1 x2
x1 0 1
x2 0 -5
B =
u1
x1 0
x2 100
C =
x1 x2
y1 1 0
D =
u1
y1 0
【 S T E P 2 {\rm STEP2} STEP2】:判断控制系统的可控性和可观性。
% STEP2:判断系统的可控性和可观性
ctrl_matrix=ctrb(A,B); % 可控性矩阵
R1=rank(ctrl_matrix);
if (R1 == 2)
disp('系统完全可控!');
else
disp('系统不可控!');
end
observe_matrix=obsv(A,C); % 可观性矩阵
R2=rank(observe_matrix);
if (R2 == 2)
disp('系统完全可观!');
else
disp('系统不可观!');
end
% MATLAB结果:
% 系统完全可控!
% 系统完全可观!
【 S T E P 3 {\rm STEP3} STEP3】:求状态反馈矩阵,进行状态反馈。
根据设计要求,闭环阻尼比 ζ = 0.707 \zeta=0.707 ζ=0.707,无阻尼自然振荡频率 ω c = 10 r a d / s \omega_c=10{\rm rad/s} ωc=10rad/s,可得闭环系统的期望极点为: s 1 , 2 = − 7.07 ± j 7.07 s_{1,2}=-7.07±{\rm j}7.07 s1,2=−7.07±j7.07;
因此,系统特征多项式为: ( s − s 1 ) ( s − s 2 ) = s 2 + 14.14 s + 100 (s-s_1)(s-s_2)=s^2+14.14s+100 (s−s1)(s−s2)=s2+14.14s+100;
假设二维状态反馈矩阵为: K = [ k 1 , k 2 ] K=\begin{bmatrix}k_1,k_2\end{bmatrix} K=[k1,k2],则反馈后的闭环系统特征多项式为:
det [ s I − ( A − B K ) ] = det [ s − 1 100 k 1 s + 5 + 100 k 2 ] \det[sI-(A-BK)]=\det\begin{bmatrix} s & -1\\ 100k_1 & s+5+100k_2 \end{bmatrix} det[sI−(A−BK)]=det[s100k1−1s+5+100k2]
根据 ( s − s 1 ) ( s − s 2 ) = det [ s I − ( A − B K ) ] (s-s_1)(s-s_2)=\det[sI-(A-BK)] (s−s1)(s−s2)=det[sI−(A−BK)],求得状态反馈矩阵: K = [ 1 , 0.914 ] K=\begin{bmatrix}1,0.914\end{bmatrix} K=[1,0.914];
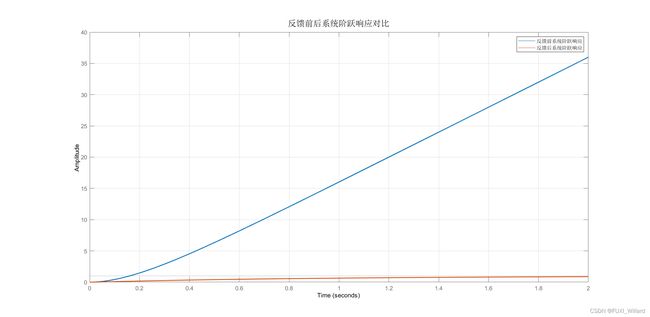
【 S T E P 4 {\rm STEP4} STEP4】:对反馈前后的系统进行对比分析。
% STEP4:对状态反馈前后的系统进行对比分析
K=[1,0.914]; % 状态反馈矩阵K
stateFeedback=A-B*K;
sysStateFeedback=ss(stateFeedback,B,C,D)
syms s;
det(s*eye(2)-stateFeedback) % 状态反馈后系统特征多项式
figure(1);
step(sys);hold on;
step(sysStateFeedback,2);grid on;
legend('反馈前系统阶跃响应','反馈后系统阶跃响应');
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('反馈前后系统阶跃响应对比','FontSize',15);
figure(2);
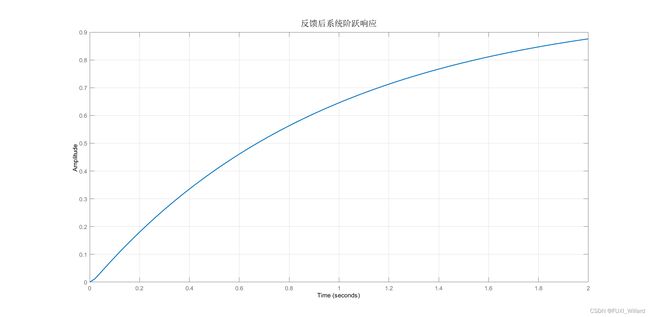
step(sysStateFeedback,2);grid;
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('反馈后系统阶跃响应','FontSize',15);
% 结果:
sysStateFeedback =
A =
x1 x2
x1 0 1
x2 -100 -96.4
B =
u1
x1 0
x2 100
C =
x1 x2
y1 1 0
D =
u1
y1 0
Continuous-time state-space model.
ans =
s^2 + (482*s)/5 + 100
【完整代码】
% 实例Chapter9.4.6.1
clc;clear;
% STEP1:建立控制系统状态空间模型
A=[0,1;0,-5];B=[0;100];
C=[1,0];D=0;
sys=ss(A,B,C,D)
% STEP2:判断系统的可控性和可观性
ctrl_matrix=ctrb(A,B); % 可控性矩阵
R1=rank(ctrl_matrix);
if (R1 == 2)
disp('系统完全可控!');
else
disp('系统不可控!');
end
observe_matrix=obsv(A,C); % 可观性矩阵
R2=rank(observe_matrix);
if (R2 == 2)
disp('系统完全可观!');
else
disp('系统不可观!');
end
% STEP4:对状态反馈前后的系统进行对比分析
K=[1,0.914]; % 状态反馈矩阵K
stateFeedback=A-B*K;
sysStateFeedback=ss(stateFeedback,B,C,D)
syms s;
det(s*eye(2)-stateFeedback) % 状态反馈后系统特征多项式
figure(1);
step(sys);hold on;
step(sysStateFeedback,2);grid on;
legend('反馈前系统阶跃响应','反馈后系统阶跃响应');
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('反馈前后系统阶跃响应对比','FontSize',15);
figure(2);
step(sysStateFeedback,2);grid;
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('反馈后系统阶跃响应','FontSize',15);