Python+人工智能基础班（通俗易懂版教学）

Python+人工智能基础班（通俗易懂版教学）_人工智能基础入门教程_人工智能机器学习

一、环境及工具包的介绍

后续的启动都是由Anaconda中直接launch来启动jupyter notebook
开发环境


工具包

二、Python基本语法

1. 基本运算

2. 列表生成

3. 函数

4. 模块引入

三、matplotlib、numpy、pandas实操

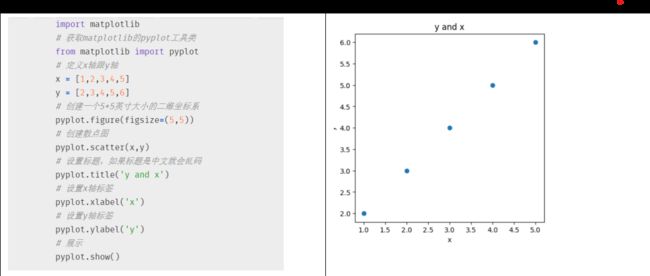
1. Matplotlib实现可视化
matplotlib使用介绍
下载 打开Anaconda Powershell prompt命令窗口下载

使用


2. numpy实现数组运算
numpy使用介绍




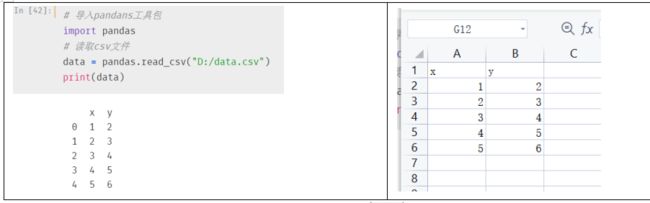
3. pandas实现数据快速的导入导出
pandas使用介绍

四、机器学习介绍

1. 机器学习的基本概念

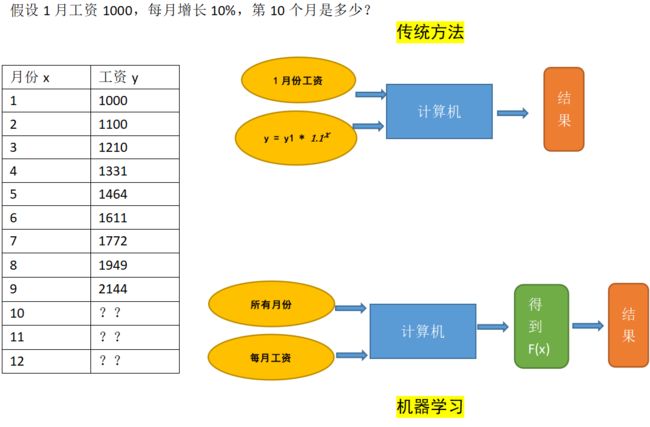
这就是机器学习，计算机不用你告诉它根据什么函数计算出来的，计算机自己会拟合出函数，然后根据自己的函数计算出结果。

2. 机器学习的类别
1. 监督机器学习算法
当一个孩子逐渐认识事物的时候，父母给他一些苹果和橘子(目标值)，并且告诉他苹果是什么样的，有哪儿些特征(特征值)，橘子是什么样的，有哪儿些特征(特征值)。经过父母的不断介绍，这个孩子已经知道苹果和橘子的区别，如果孩子在看到苹果和橘子的时候给出错误的判断，父母就会指出错误的原因（人工干预），经过不断地学习，再见到苹果和橘子的时候，孩子立即就可以做出正确的判断。

2. 无监督机器学习算法
同样的一个孩子，在一开始认识事物的时候，父母会给他一些苹果和橘子，但是并不告诉他哪儿个是苹果，哪儿个是橘子，而是让他自己根据两个事物的特征自己进行判断，会把苹果和橘子分到两个不同组中，下次再给孩子一个苹果，他会把苹果分到苹果组中，而不是分到橘子组中。

3. 强化机器学习算法

五、机器学习线性回归

1. 回归分析
根据数据确定两种或两种以上变量间相互依赖的定量关系

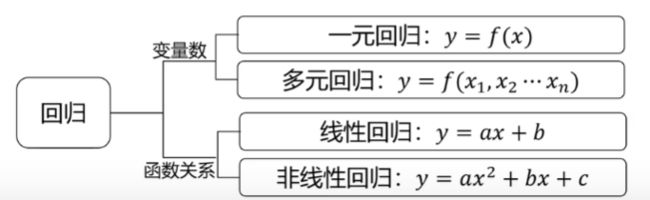
2. 线性回归求解

3. 损失函数
通过损失函数比较最适合的a和b

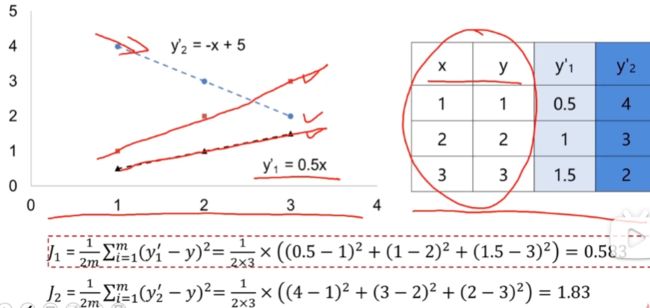
4. 梯度下降法
上面损失函数可以用来比较两个线性方程，哪个方程的a和b更合适，但是梯度下降法可以寻找到损失函数的极小值。

梯度下降法的含义就是：通过一个求导来确定当前p_i点的导数值，并且通过0.01来缩放导数值。然后再通过p _i 减去缩放后的导数值就可以得到更接近极小值点的p _i+1

这里就不断地使用梯度下降法来找到极小值点

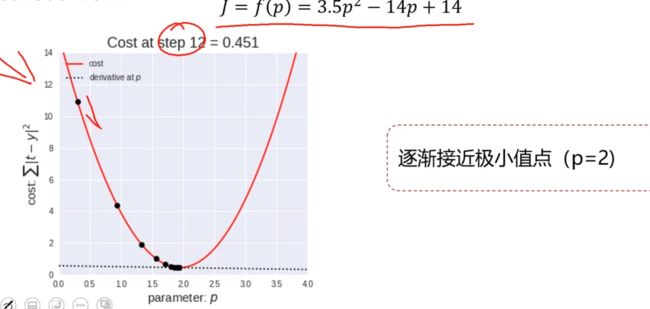
5. 应用梯度下降法，在损失函数中找到极小值
重复计算是指每个计算出来的tempa和tempb都赋值给a和b，重复这个动作直到计算的tempa和tempb值不怎么变化，就算是收敛了。

线性回归实战准备

1. sklearn算法库
sklearn算法库使用介绍
从上述损失函数跟梯度下降的运算过程来看，不编写个百来行代码是无法计算出结果的，但是如果使用了sklearn算法库，大概使用五行代码就能实现。

2. 通过sklearn求解线性回归问题

# 寻找a、b
from sklearn.linear_model import LinearRegression
lr_model = LinearRegression()
lr_model.fit(x,y)

# 展示a、b
a = lr_model.coef_
b = lr_model.intercept_

#对新数据做预测
predictions = lr_model.predict(x_new)

3. 模型评估
对于线性回归方程，主要有以下三种评估方法

均方误差（MSE）
MSE值越小越好，最小可以是0，但无法达到0

R方值
R方值越大越好，最大可以是1，但无法达到1

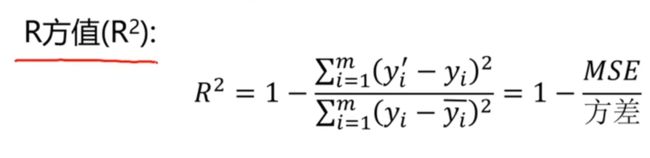
4. 图形展示
注意：左边四个散点图跟右边的多张图同时展示的代码不匹配的，只是对pyplot.subplot函数做介绍

单因子线性回归实战

任务：基于generated_data.csv数据，建立线性回归模型，预测x=3.5对应的y值。

# 将csv文件导入
import pandas
data = pandas.read_csv('C:/Users/liguojun/Desktop/AI_Data_Set/generated_data.csv')

# 测试数据是否导入
x = data.loc[:,'x']
y = data.loc[:,'y']
from matplotlib import pyplot
pyplot.figure(figsize=(10,10))
pyplot.scatter(x,y)

# 将x、y维度转换，因为后面的fit需要x和y是二维数组
import numpy
x=numpy.array(x)
x=x.reshape(-1,1)
y=numpy.array(y)
y=y.reshape(-1,1)

# 导入sklearn工具包，并且使用线性回归
from sklearn.linear_model import LinearRegression
# 创建模型并返回实例
lr_model = LinearRegression()
# 训练数据集，但是这里需要x和y是二维数组
lr_model.fit(x,y)

# 拟合完后看看效果
y_3 = lr_model.predict([[3.5]])
print(y_3)

# 查看线性回归得到的a和b
a = lr_model.coef_
b = lr_model.intercept_
print(a,b)

# 模型评估
from sklearn.metrics import mean_squared_error, r2_score
y_predict = lr_model.predict(x)
MSE = mean_squared_error(y,y_predict)
R2 = r2_score(y,y_predict)
print(MSE, R2)

运行结果

多因子线性回归实战

1. 对数据进行可视化

# 导入数据
import pandas as pd
import numpy as np
data = pd.read_csv('C:/Users/liguojun/Desktop/AI_Data_Set/usa_housing_price.csv')

# 导入可视化工具包
%matplotlib inline
from matplotlib import pyplot as plt
# 定制一个10*10英寸的二维坐标系
fig = plt.figure(figsize=(10,10))
# 定制两行三列，并把fig1放在第一个位置
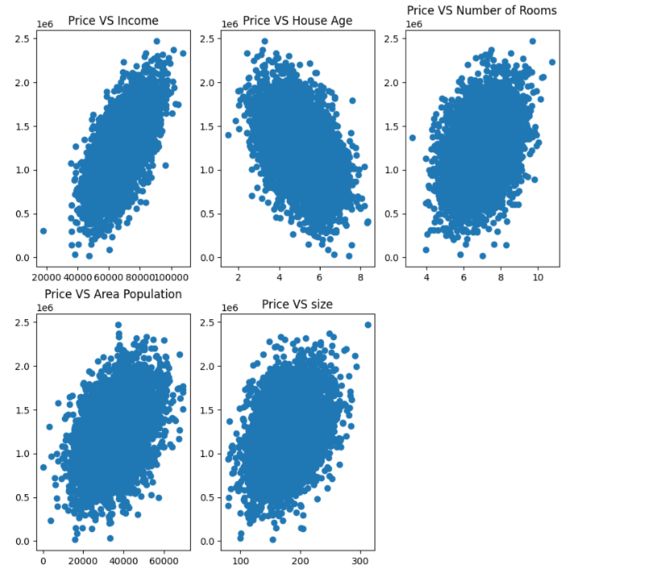
# 绘制散点图，Avg. Area Income做x轴，Price做y轴，并且设置标题
fig1 = plt.subplot(231)
plt.scatter(data.loc[:,'Avg. Area Income'], data.loc[:,'Price'])
plt.title('Price VS Income')

fig2 = plt.subplot(232)
plt.scatter(data.loc[:,'Avg. Area House Age'], data.loc[:,'Price'])
plt.title('Price VS House Age')

fig3 = plt.subplot(233)
plt.scatter(data.loc[:,'Avg. Area Number of Rooms'], data.loc[:,'Price'])
plt.title('Price VS Number of Rooms')

fig4 = plt.subplot(234)
plt.scatter(data.loc[:,'Area Population'], data.loc[:,'Price'])
plt.title('Price VS Area Population')

fig5 = plt.subplot(235)
plt.scatter(data.loc[:,'size'], data.loc[:,'Price'])
plt.title('Price VS size')

2. 训练模型、预测数据、模型评估

# 建立多变量，X_multi是包含除Price列之外的所有列
X_multi = data.drop(['Price'],axis = 1)
y = y = data.loc[:,'Price']
# 导入sklearn工具包，并且使用线性回归
from sklearn.linear_model import LinearRegression
# 获取线性回归模型
LR_multi = LinearRegression()
# 使用多变量来训练模型
LR_multi.fit(X_multi,y)
# 预测
y_predict_multi = LR_multi.predict(X_multi)
print(y_predict_multi)

# 模型评估
from sklearn.metrics import mean_squared_error, r2_score
MSE = mean_squared_error(y,y_predict_multi)
R2 = r2_score(y,y_predict_multi)
print(MSE, R2)

3. 预测房屋售价
预测Income=65000，House Age=5，Number of Rooms=5， Population=30000，size=200的合理房价

X_test = [65000,5,5,30000,200]
X_test = np.array(X_test).reshape(1,-1)
y_test_predict = LR_multi.predict(X_test)
print(y_test_predict)

六、机器学习逻辑回归

使用线性回归解决分类任务

1. 分类任务
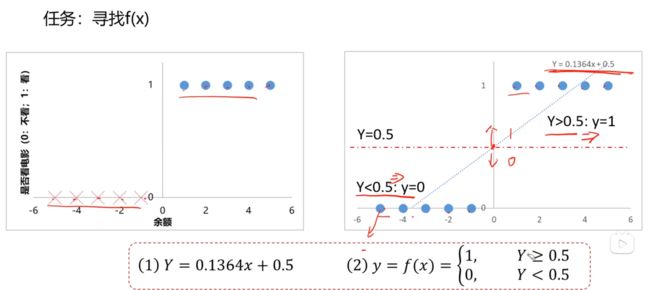
小明如果余额为正，那么就会分类到看电影。
小明如果余额为负，那么就会分类到不看电影。

2. 使用线性回归解决

首先对离散的节点拟合出函数（1），然后再通过函数（2）来分类

将数据集放入模型中训练，然后将新的数据放入进行预测。

3. 线性回归出现的问题

使用逻辑回归解决分类任务

重点就是找到这个g(x)函数



损失函数判断拟合效果

梯度下降法寻找最小损失函数

评估模型

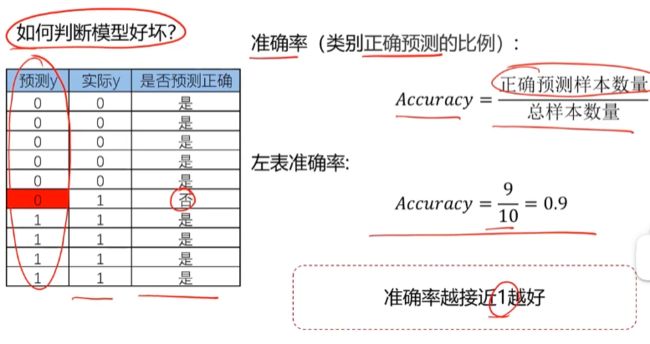
逻辑回归实战：考试通过预测

任务：基于examdata.csv数据，建立逻辑回归模型，预测Exam1=75，Exam2=60时，该同学在Exam3是passed还是failed；
1. 导入数据

# 导入数据
import pandas as pd
import numpy as np
data = pd.read_csv('C:/Users/liguojun/Desktop/AI_Data_Set/examdata.csv')

# 查看数据
%matplotlib inline
from matplotlib import pyplot as plt
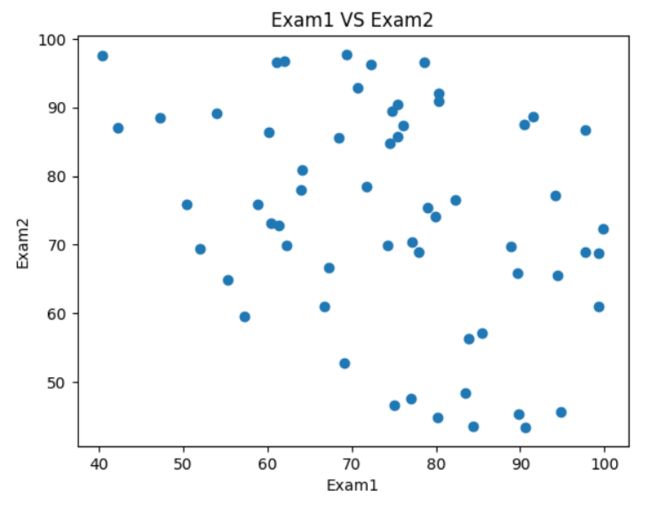
fig1 = plt.figure()
plt.scatter(data.loc[:,'Exam1'],data.loc[:,'Exam2'])
plt.xlabel('Exam1')
plt.ylabel('Exam2')
plt.title('Exam1 VS Exam2')

2. 只输出Pass等于1的数据

# 如果Pass列中值为1，那么这一行就设置为true
mask = data.loc[:,'Pass'] == 1

# mask为true的那一行数据才会被显示出来
fig2 = plt.figure()
plt.scatter(data.loc[:,'Exam1'][mask],data.loc[:,'Exam2'][mask])
plt.xlabel('Exam1')
plt.ylabel('Exam2')
plt.title('Exam1 VS Exam2')

3. 将Pass不同值的点分开

# mask=true和mask=false两种数据分类
fig3 = plt.figure()
# 会自动分颜色
passed = plt.scatter(data.loc[:,'Exam1'][mask],data.loc[:,'Exam2'][mask])
failed = plt.scatter(data.loc[:,'Exam1'][~mask],data.loc[:,'Exam2'][~mask])
plt.xlabel('Exam1')
plt.ylabel('Exam2')
plt.title('Exam1 VS Exam2')

4. 训练模型

# 定义训练模型的数据集
x = data.drop(['Pass'],axis=1)
y = data.loc[:,'Pass']
x1 = data.loc[:,'Exam1']
x2 = data.loc[:,'Exam2']

# 训练模型
from sklearn.linear_model import LogisticRegression
LR = LogisticRegression()
LR.fit(x,y)

# 预测结果
y_predict = LR.predict(x)
print(y_predict)

5. 评估模型

from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y,y_predict)
print(accuracy)

6. 预测数据

# 预测exam1=70，exam2=65
y_test = LR.predict([[70,65]])
print(y_test)

7. 获取系数

# 获取系数
theta0 = LR.intercept_
theta1, theta2 = LR.coef_[0][0],LR.coef_[0][1]
print(theta0,theta1,theta2)

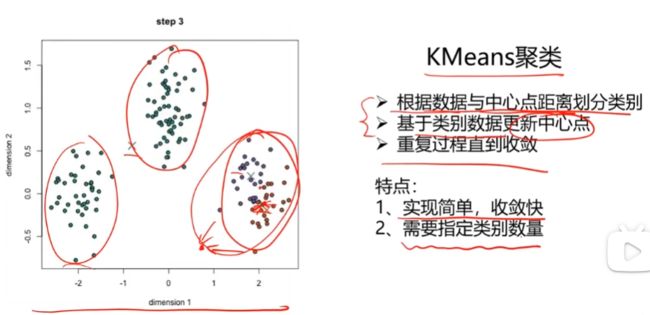
七、机器学习聚类分析

常用聚类算法

1. KMeans聚类

2. KNN最近邻分类模型
给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的K个实例（也就是上面所说的K个邻居）

3. Meanshift均值漂移聚类

4. DBSCAN基于密度的空间聚类算法

---

预测结果矫正

因为聚类是无监督学习，所以label0、label1、label2这个标签并不是固定在一堆数据中，所以在散点图与中心点的label需要矫正

KMeans算法实战

任务：采用Kmeans算法实现2D数据自动聚类，预测V1=80，V2=60数据类别，计算预测准确率，完成结果矫正
1. 导入并查看数据集

import pandas as pd
import numpy as np
data = pd.read_csv('C:/Users/liguojun/Desktop/AI_Data_Set/data.csv')
data.head()

2. 根据labels分类

# 定义训练数据
x = data.drop(['labels'], axis=1)
y = data.loc[:,'labels']
x.head()
pd.value_counts(y)

3. 观察散点图

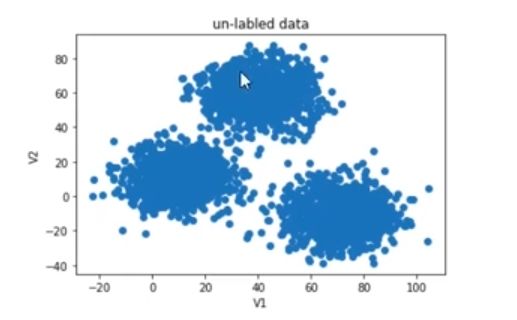
# 画出散点图
%matplotlib inline
from matplotlib import pyplot as plt
fig1 = plt.figure()
plt.scatter(x.loc[:,'V1'],x.loc[:,'V2'])
plt.title("un-labled data")
plt.xlabel('V1')
plt.ylabel('V2')
plt.show()

4. 分类显示散点图

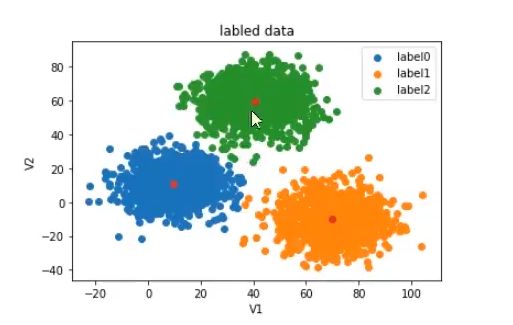
fig1 = plt.figure()
label0 = plt.scatter(x.loc[:,'V1'][y==0],x.loc[:,'V2'][y==0])
label1 = plt.scatter(x.loc[:,'V1'][y==1],x.loc[:,'V2'][y==1])
label2 = plt.scatter(x.loc[:,'V1'][y==2],x.loc[:,'V2'][y==2])
plt.title("labled data")
plt.xlabel('V1')
plt.ylabel('V2')
plt.legend((label0,label1,label2),('label0','label1','label2'))
plt.show()

5. 训练模型

# 获取聚类模型
from sklearn.cluster import KMeans
# K为3
KM = KMeans(n_clusters=3, random_state=0)
# 训练模型
KM.fit(x)

6. 获取中心点

# 展示聚类模型训练之后的三个中心点
centers = KM.cluster_centers_

7. 将散点图跟中心点放在一起看看效果

# 将三个中心点放入数据中展示
fig3 = plt.figure()
label0 = plt.scatter(x.loc[:,'V1'][y==0],x.loc[:,'V2'][y==0])
label1 = plt.scatter(x.loc[:,'V1'][y==1],x.loc[:,'V2'][y==1])
label2 = plt.scatter(x.loc[:,'V1'][y==2],x.loc[:,'V2'][y==2])
plt.title("labled data")
plt.xlabel('V1')
plt.ylabel('V2')
plt.legend((label0,label1,label2),('label0','label1','label2'))

plt.scatter(centers[:,0],centers[:,1])
plt.show()

8. 查看预测数据
发现预测数据的结果跟实际值不一样

# 测试预测数据
y_predict_test = KM.predict([[80,60]])
print(y_predict_test)

9. 查看准确率

# 获取准确率
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y,y_predict)
print(accuracy)

10. 查看哪里出现差错

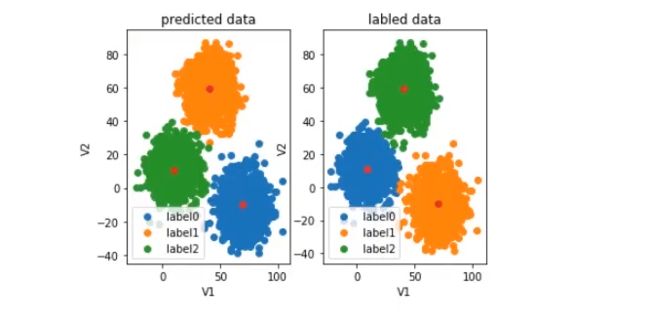
fig5 = plt.subplot(121)
label0 = plt.scatter(x.loc[:,'V1'][y==0],x.loc[:,'V2'][y==0])
label1 = plt.scatter(x.loc[:,'V1'][y==1],x.loc[:,'V2'][y==1])
label2 = plt.scatter(x.loc[:,'V1'][y==2],x.loc[:,'V2'][y==2])
plt.title("predicted data")
plt.xlabel('V1')
plt.ylabel('V2')
plt.legend((label0,label1,label2),('label0','label1','label2'))
plt.scatter(centers[:,0],centers[:,1])

fig6 = plt.subplot(122)
label0 = plt.scatter(x.loc[:,'V1'][y==0],x.loc[:,'V2'][y==0])
label1 = plt.scatter(x.loc[:,'V1'][y==1],x.loc[:,'V2'][y==1])
label2 = plt.scatter(x.loc[:,'V1'][y==2],x.loc[:,'V2'][y==2])
plt.title("labled data")
plt.xlabel('V1')
plt.ylabel('V2')
plt.legend((label0,label1,label2),('label0','label1','label2'))
plt.scatter(centers[:,0],centers[:,1])

发现label错乱了

---

11. 预测结果纠正

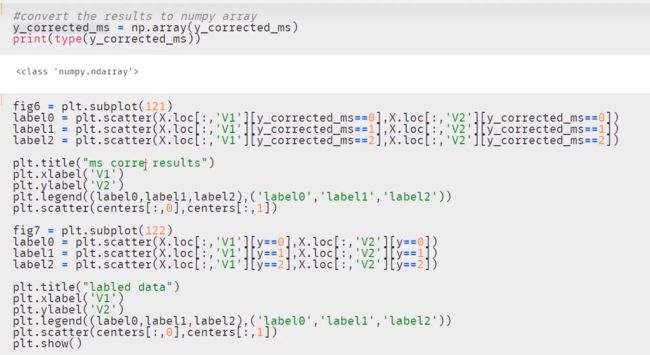
# 预测结果矫正
y_corrected =[]
for i in y_predict:
    if i==0:
        y_corrected.append(1)
    elif i==1:
        y_corrected.append(2)
    else:
        y_corrected.append(0)
print(pd.value_counts(y_corrected),pd.value_counts(y))

12. 重新计算准确率

# 重新计算准确率
print(accuracy_score(y,y_corrected))

KNN算法实战

1. 获取KNN算法模型并训练模型

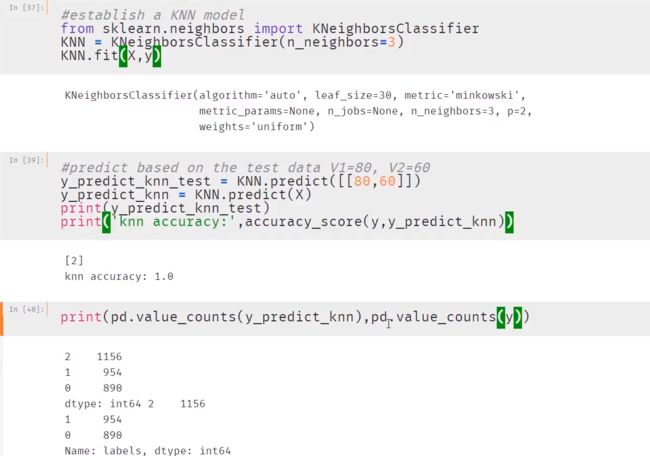
==2.查看效果 ==
因为KNN算法是监督式算法，所以label不会混乱


3. 预测结果并计算准确率

Meanshift算法实战

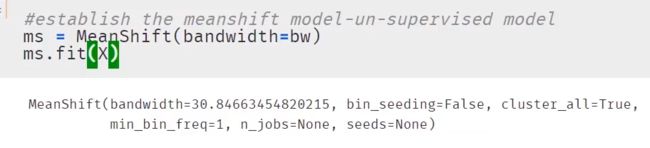
1. 确定样本数量以及估算半径
对x数据集的样本数量为500，估算半径为30.84663454820215

2. 创建Meanshift模型

3. 预测数据
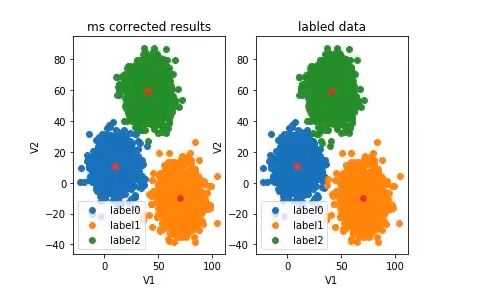
发现label又出现了混乱

4. 查看散点图

fig5 = plt.subplot(121)
label0 = plt.scatter(x.loc[:,'V1'][y==0],x.loc[:,'V2'][y==0])
label1 = plt.scatter(x.loc[:,'V1'][y==1],x.loc[:,'V2'][y==1])
label2 = plt.scatter(x.loc[:,'V1'][y==2],x.loc[:,'V2'][y==2])
plt.title("predicted data")
plt.xlabel('V1')
plt.ylabel('V2')
plt.legend((label0,label1,label2),('label0','label1','label2'))
plt.scatter(centers[:,0],centers[:,1])

fig6 = plt.subplot(122)
label0 = plt.scatter(x.loc[:,'V1'][y==0],x.loc[:,'V2'][y==0])
label1 = plt.scatter(x.loc[:,'V1'][y==1],x.loc[:,'V2'][y==1])
label2 = plt.scatter(x.loc[:,'V1'][y==2],x.loc[:,'V2'][y==2])
plt.title("labled data")
plt.xlabel('V1')
plt.ylabel('V2')
plt.legend((label0,label1,label2),('label0','label1','label2'))
plt.scatter(centers[:,0],centers[:,1])

5. 根据上述散点图进行纠正

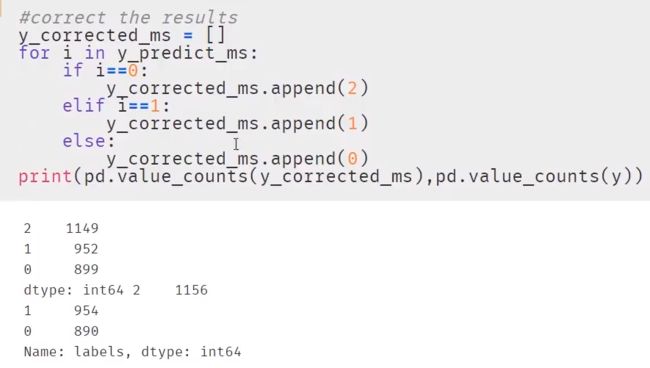
6. 根据纠正后的结果查看散点图

八、机器学习决策树

决策树介绍

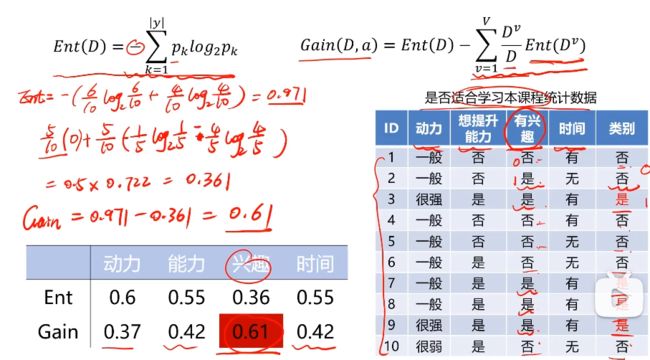
目标：划分后样本分布不确定性尽可能小，即划分后信息熵小，信息增益大
总结：哪个属性分类后信息更集中就先选择哪个属性进行分类
算法：ID3、C4.5、CART

决策树实战准备

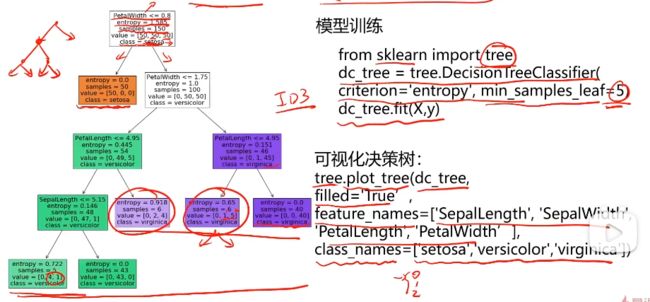
entropy：信息熵
samples：样本数量
value：根据class分类后每个种类的不同值
class：种类

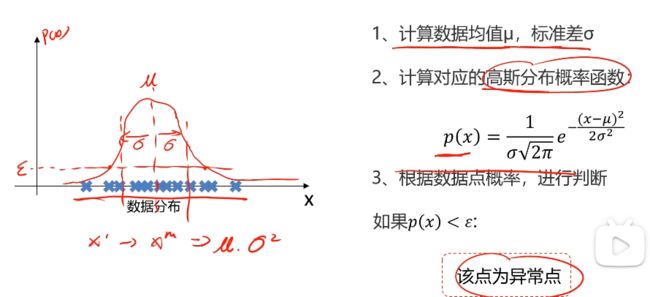
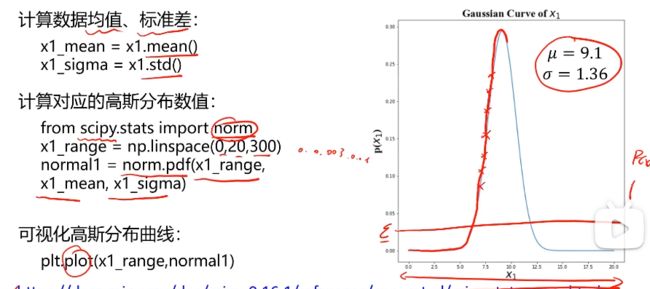
九、机器学习异常检测

异常检测介绍

基于高斯分布实现异常检测

异常数据检测实战准备

十、机器学习主成分分析PCA

主成分分析介绍

主成分分析用于实现数据降维，数据降维可以减少模型分析数据量，提升处理效率，降低计算难度，实现数据可视化（因为高纬度无法进行数据可视化）

主成分分析实战准备

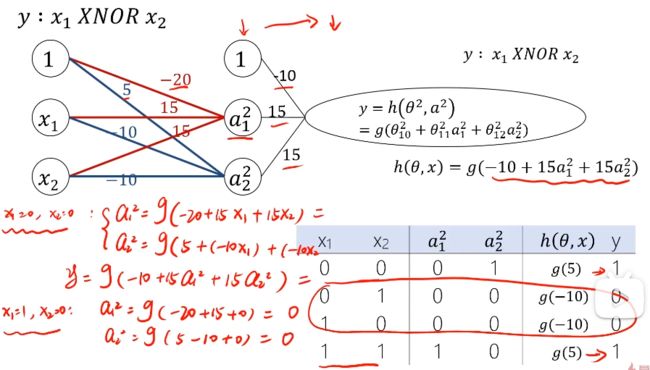
十一、深度学习之多层感知机MLP

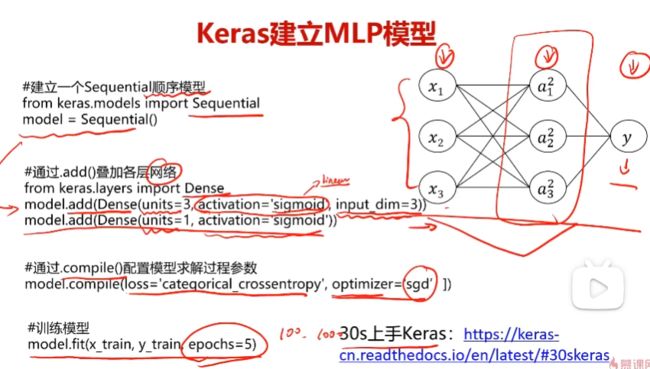
多层感知机MLP介绍

多层感知机MLP实现单一非线性分类

1. AND运算

2. 同或运算

多层感知机MLP实现多分类预测

多层感知机MLP实战准备

十二、总结

在学习了部分章节之后，我觉得本门课程后面的学习都是讲知识点，然后做实战准备，最后实战。所以我认为有了前面的几个算法演练之后，后面的就可以省略，思路大致掌握就可以了，后面遇到新的算法再去学习就行了。