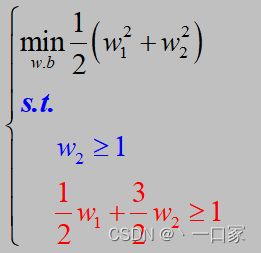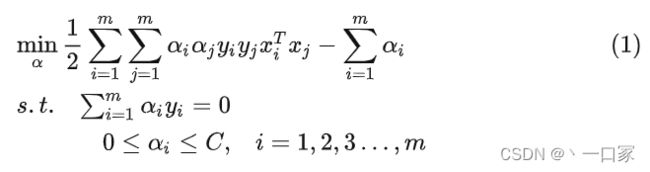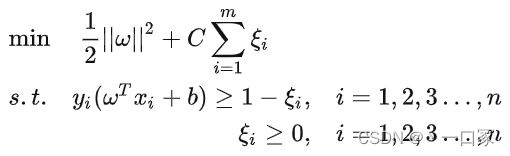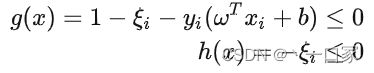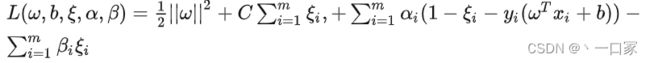机器学习：支持向量机（SVM）

简介

支持向量机（support vector machines，SVM）是一种二分类模型，它将实例的特征向量映射为空间中的一些点，SVM 的目的就是想要画出一条线，以 “最好地” 区分这两类点，以至如果以后有了新的点，这条线也能做出很好的分类。SVM 适合中小型数据样本、非线性、高维的分类问题。

SVM 最早是由 Vladimir N. Vapnik 和 Alexey Ya. Chervonenkis 在1963年提出，目前的版本（soft margin）是由 Corinna Cortes 和 Vapnik 在1993年提出，并在1995年发表。深度学习（2012）出现之前，SVM 被认为机器学习中近十几年来最成功，表现最好的算法。
 

最大分类与间隔

先举一个例子：

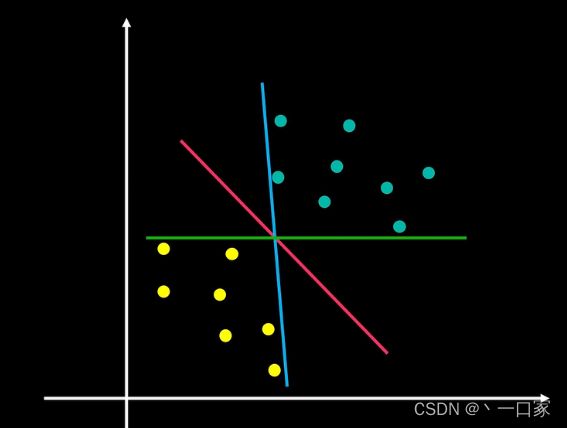
下面的二维平面中中我们应取三条直线中的哪一条来分割两类颜色种类不同的点呢？

这个问题同样可以延申到三维空间中找一个二维平面区分两类数据，也可以再进一步推演到更高维的空间中找一个超平面区分两类数据。这样问题就是两类维度数据，有n个样本，每个样本有m个维度，如何设计一个维度数为m-1的超平面即决策边界将两类数据区分开来。

为了便于直观理解我们仍以上图的二维空间问题为例。

若选取蓝色或绿色直线，我们可以看出两类数据都有相应的数据点与决策边界非常接近。当我们有一新的数据同样接近该直线，这样分类错误的概率是非常大的，因此这种画法非常危险。

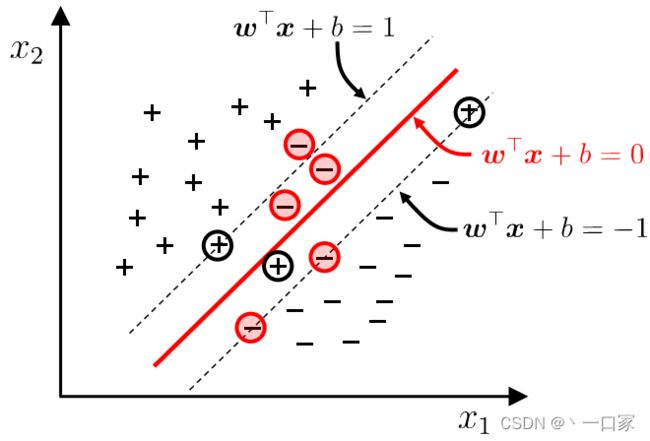
若选取红色直线，我们可以看出两类数据中所有的点都与决策边界保持了一定距离，这个距离取到了缓冲区的作用，当这个缓冲区足够大时分类结果的可信度就很高了。我们把这个缓冲区称为间隔，越大的间隔意味着两类数据的差异越大，我们区分起来就越容易。因此寻找最佳决策边界线的问题可以转化为求解两类数据的最大间隔问题。

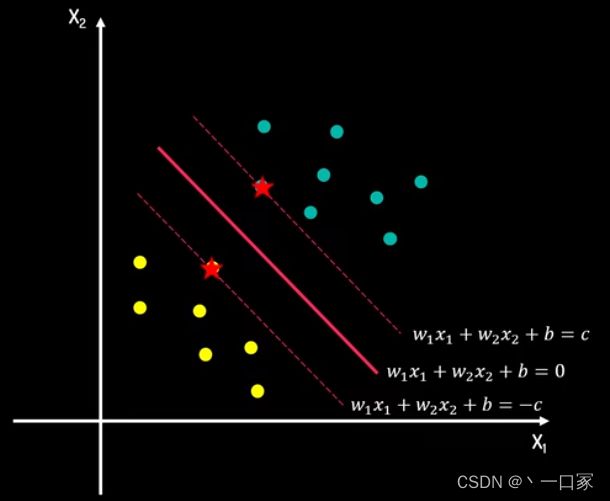
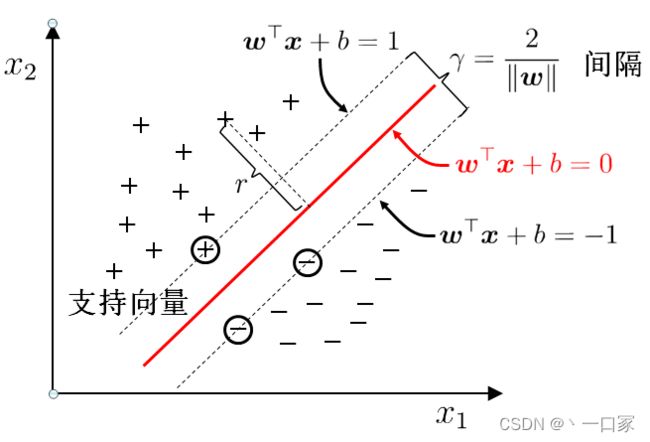
假设决策边界的超平面方程式为w1+w2+b=0，它上下分别移动c来到对于的间隔上下边界w1+w2+b=c或w1+w2+b=-c。由于上下边界一点会经过一些样本数据点，而这些点距离决策边界最近，它们决定了间隔距离，我们称它们为支持向量，这也是为什么我们将该方法称之为支持向量机（SVM）。把上述超平面方程式同时除以c，则方程右侧被转化为+-1，则我们可将上述超平面分为正超平面w1+w2+b=1，负超平面w1+w2+b=-1以及决策超平面1+w2+b=0。所有正超平面及其上方的数据点颜色相同，都属于正类；负超平面及其下方的点为负类。

那么我们应该如何求解两类数据的最佳超平面呢？下面以下图中示例进行推导得出最佳超平面。

假设划分超平面的线性方程为：，其中  为法向量，决定了超平面的方向； 为位移项，决定了超平面与源点之间的距离。显然划分超平面可被法向量  和位移  决定。根据点到平面的距离公式d=|Ax0+By0+Cz0+D|/√(A²+B²+C²)，空间中任意点到超平面 的距离可写为，其中为w向量的各个元素的平方和的开平方.

又有定义：（其中和分别是第i个样本和第i个样本值所对应的目标值）

为函数距离；

所以我们把函数距离和点到面的距离进行一个综合，就变成了：

为数据集与分隔超平面的几何距离；

又因为y的取值是1或-1，这就保证了如果样本分类正确，则这个值是一个正数；如果样本分类错误，这个值是一个负数。这很好理解，分类对了就是同一边，就为正数，即公式如下：

在训练的时候我们要求限制条件更严格点以使最终得到的分类器鲁棒性更强，所以为了提高容错率我们将上述公式稍加改变为

将该公式变式为。

记超平面上的正样本为，超平面的负样本为。则根据向量的加减法规则减去得到的向量在最佳超平面的法向量方向的投影即为“间隔” 。

而，

将这两个式子带入中得到。

也就是说使两类样本距离最大的因素仅仅和最佳超平面的法向量有关。要找到具有“最大间隔”（maximum margin）的最佳超平面就是找到能满足上述式子中约束的参数 w，b使得最大，即：。由上式进行变式，为了最大化间隔，仅需最大化   ，这等价于最小化 。

因此就是SVM的基本型。

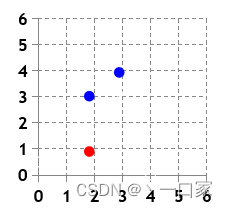
以下举一个二维平面中的例子。已知在二维平面上有三个点分别为（2，3），（3，4），     （2，1）；这三个点的标签分别为+1，+1，-1。请求解出最佳分割平面。

 

首先由SVM基本型可知问题可转换成：

 消去b得：

 将约束条件几何化如下图，又显然可看为为圆的方程式的左半部分，故在几何平面上可翻译为找出在约束条件下以原点为圆心半径最小的圆。

如上图知在约束条件下以原点为圆心的圆显然与直线w2=1相切时半径最小，故w1=0。又显然负超平面必然经过点（2，1），

正超平面必然经过点（2，3）。故有，，代入w1=0，得w2=1，b=-2。

故最佳超平面为。

但是以上求解最佳超平面的方法只适用于样本点较少的情况。那我们该如何处理更多样本点呢？

 

对偶问题

给定一个目标函数 f : Rn→R，希望找到xRn，在满足约束条件g(x)=0的前提下，使得f(x)有最小值。该约束优化问题记为：可建立拉格朗日函数：

 其中 λ 称为拉格朗日乘数。因此，可将原本的约束优化问题转换成等价的无约束优化问题：分别对待求解参数求偏导，可得：一般联立方程组可以得到相应的解。

将约束等式 g(x)=0 推广为不等式 g(x)≤0。这个约束优化问题可改为：

同理，其拉格朗日函数为：。其约束范围为不等式，因此可等价转化成Karush-Kuhn-Tucker (KKT)条件：

在此基础上，通过优化方式（如二次规划或SMO）求解其最优解。

 

核函数

首先我们来介绍一下核函数的概念，可能大家会很好奇，明明我们已经把SVM模型的原理完整推导完了，怎么又冒出来一个核函数。实际上核函数非常精彩，它对于SVM也非常重要，因为它奠定了SVM的“江湖地位”，也可以说是SVM模型最大的特性。

在介绍核函数之前，我们先来看一个问题，这个问题在机器学习的历史上非常有名，叫做异或问题。我们都知道，在二进制当中有一个操作叫做亦或操作。亦或操作其实很简单，就是如果两个数相同返回的结果就是0，否则就返回1。如果我们的数据是类似亦或组成的，就会是这样一个形状：

 

我们观察一下上面这个图，会发现一个问题，就是我们无论如何也不可能找到一条线把上面这个分类完成。因为一条线只能分出两个区域，但是上面这个图明显有四个区域。

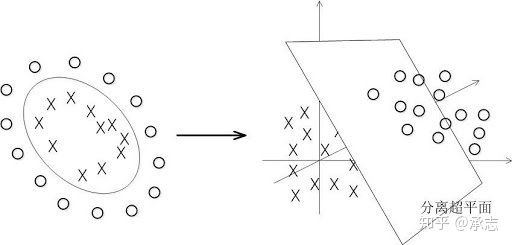
那如果我们把上面的数据映射到更高的维度当中，上图是二维的图像，我们把它映射到三维当中，就可以使用一个平面将样本区分开了。也就是说通过一个映射函数，将样本从n维映射到n+1或者更高的维度，使得原本线性不可分的数据变成线性可分，这样我们就解决了一些原本不能解决的问题。

所以核函数是什么？是一系列函数的统称，这些函数的输入是样本x，输出是一个映射到更高维度的样本。大部分能实现这一点的函数都可以认为是核函数（不完全准确，只是为了理解方便），当然一些稀奇古怪的函数虽然是核函数，但是对我们的价值可能并不大，所以我们也很少用，常用的核函数还是只有少数几种。 

 现在我们已经知道核函数是什么了，那么它又该如何使用呢？

这个问题也不难，数学上比较困难的是表示问题，一个问题被描述以及表示清楚可能是最难的，当表示出来了之后把它解出来可能就要简单很多了。所以我们先来表示问题，用一个字母Φ来表示核函数。前面已经说过了，核函数的输入是样本x，所以映射之后的样本就是Φ(x)。

已知由对偶问题推导出的SVM公式为：

我们要做的就是把核函数代入进去，仅此而已，代入进去之后，就会得到：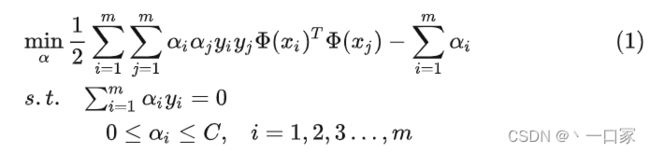

这里有一个小问题，我们前面说了函数Φ(x)会把x映射到更高的维度。比如x本身是10维的，我们用了函数之后给映射到1000维了，当然它的线性不可分的问题可能解决了，但是这会带来另外一个问题，就是计算的复杂度增加了。因为原本本来只需要10次计算，但现在映射了之后，需要1000次计算才可以得到结果。这不符合我们想要白嫖不想花钱的心理，所以我们对核函数做了一些限制，只有可以白嫖的映射函数才被称为核函数。我们把需要满足的条件写出来，其实很简单。我们把满足条件的核函数称为K，那么K应该满足：

也就是说K对的结果进行计算等价于映射之后的结果再进行点乘操作，这样就可以在计算复杂度不变的情况下完成映射。其实对于核函数是有数学上的定义的，这里我没放出来，一个是觉得表示太复杂用不到，另外一个是在面试的时候其实也不会问到这么细，我们只需要知道它的性质就可以了。因为常见使用的核函数来来回回基本上也就那么几种，我们记住它们就OK了。

下面我们就来看一下常见的核函数，大概有这么四种：

1.线性核函数，其实就是没有核函数。我们表示出来就是

2.多项式核函数，它等价于一个多项式变换：这里的，b和d都是我们设置的参数

3.高斯核，这种核函数使用频率很高，

4.sigmoid核，它的公式是：

 

软间隔

在实际的场景当中，数据不可能是百分百线性可分的，即使真的能硬生生地找到这样的一个分隔平面区分开样本，那么也很有可能陷入过拟合当中，也是不值得追求的。

因此，我们需要对分类器的标准稍稍放松，允许部分样本出错。但是这就带来了一个问题，在硬间隔的场景当中，间隔就等于距离分隔平面最近的支持向量到分隔平面的距离。那么，在允许出错的情况下，这个间隔又该怎么算呢？

为了解决这个问题，我们需要对原本的公式进行变形，引入一个新的变量叫做松弛变量。松弛变量我们用希腊字母来表示，这个松弛变量允许我们适当放松这个限制条件，我们将它变成。

也就是说对于每一条样本我们都会有一个对应的松弛变量，它一共有几种情况。 

1. =0，表示样本能够正确分类

2. 0<<1，表示样本在分割平面和支持向量之间

3. =1，表示样本在分割平面上

4. 1，表示样本异常

我们可以结合下面这张图来理解一下，会容易一些：

 

松弛变量虽然可以让我们表示那些被错误分类的样本，但是我们当然不希望它随意松弛，这样模型的效果就不能保证了。所以我们把它加入损失函数当中，希望在松弛得尽量少的前提下保证模型尽可能划分正确。这样我们可以重写模型的学习条件：

 这里的C是一个常数，可以理解成惩罚参数。我们希望||w||2尽量小，也希望∑尽量小，这个参数C就是用来协调两者的。C越大代表我们对模型的分类要求越严格，越不希望出现错误分类的情况，C越小代表我们对松弛变量的要求越低。

从形式上来看模型的学习目标函数和之前的硬间隔差别并不大，只是多了一个变量而已。这也是我们希望的，在改动尽量小的前提下让模型支持分隔错误的情况。

对于上面的式子我们同样使用拉格朗日公式进行化简，将它转化成没有约束的问题。

首先，我们确定几个值。第一个是我们要优化的目标：

第二个是不等式约束，拉格朗日乘子法当中限定不等式必须都是小于等于0的形式，所以我们要将原式中的式子做一个简单的转化：

 

最后是引入拉格朗日乘子

我们写出广义拉格朗日函数： 

我们要求的是这个函数的最值，也就是

支持向量机Python代码实例

演示数据集：

链接：https://pan.baidu.com/s/1RPPtIkioXf3CSp5eHtTVXQ

提取码：3u2b

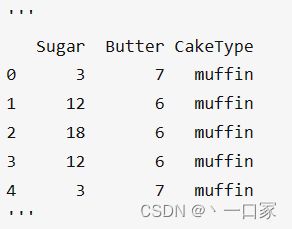
数据集是一个蛋糕配方，共有muffin和cupcake两种类型的蛋糕，配方变量为Sugar和Butter。我们需要判断，给定Sugar和Butter值，预测该蛋糕类型。

1.导入数据

#导入数据
import pandas as pd
path = "C:\\Users\\Cara\\Desktop\\cupcake or muffin.xlsx"
data = pd.read_excel(path)

数据结构大致如下：

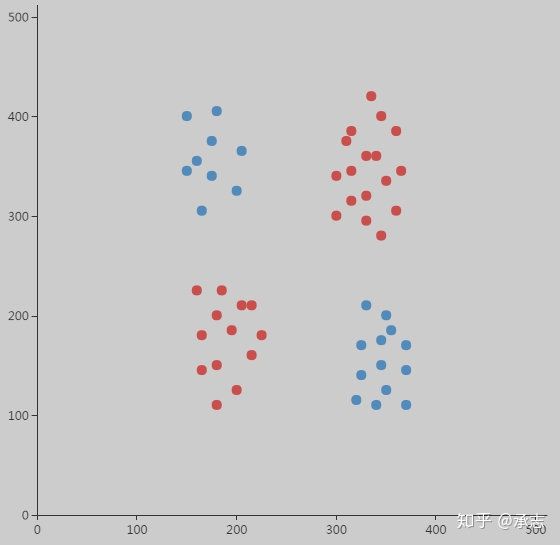
 2.数据可视化

#认识数据：数据可视化
import seaborn as sns
sns.lmplot(data=data,x='Sugar',y='Butter',palette='Set1',fit_reg=False,hue='CakeType',scatter_kws={'s':150})
'''
lmplot()参数说明：
palette='Set1'设置调色板型号，对应不同绘图风格，色彩搭配。
fit_reg=False表示不显示拟合的回归线。因为lmplot()本身是线性回归绘图函数，默认会绘制点的拟合回归线。
hue='CakeType'表示对样本点按照'CakeType'的取值不同进行分类显示，这样不同类型的蛋糕会用不同颜色显示。若不设置hue参数，则所有点都会显示为一个颜色显示。
scatter_kws={'s':150}：设置点的大小，其中s表示size。
'''

效果如下：

 

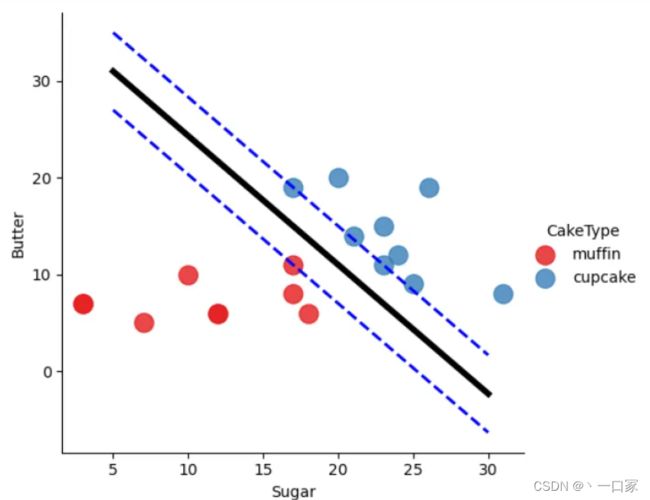
从绘图结果来看，样本数据很适合进行二分类训练，因为两种蛋糕刚好可以互相分离，使用一条直线就可以将两类样本清楚划分。而且，这样的直线不止一条，因此，我们需要找到最优的那条划分直线。 

3. 数据预处理

#数据预处理
#将CakeType的值映射到0、1，方便后续模型运算
import numpy as np
label = np.where(data['CakeType']=='muffin',0,1)

4.SVM实例化

#SVM实例化
from sklearn.svm import SVC
#SVC指Support Vector Classifier
svc = SVC(kernel='linear',C=1)
'''
SVC参数说明：
C:惩罚系数，即当分类器错误地将A类样本划分为B类了，我们将给予分类器多大的惩罚。当我们给与非常大的惩罚，即C的值设置的很大，那么分类器会变得非常精准，但是，会产生过拟合问题。
kernel：核函数，如果使用一条直线就可以将属于不同类别的样本点全部划分开，那么我们使用kernel='linear'，
如果不能线性划分开，尤其是当数据维度很多时，一般很难找到一条合适的线将不同的类别的样本划分开，那么就尝试使用高斯核函数（也称为径向基核函数-rbf）、多项式核函数（poly）
'''
svc.fit(X=x,y=label)

 5.根据拟合结果，找出超平面及其边界线并对其进行可视化

#根据拟合结果，找出超平面
w = svc.coef_[0]
a = -w[0]/w[1]#超平面的斜率，也是边界线的斜率
xx = np.linspace(5,30)#生成5~30之间的50个数
yy = a * xx - (svc.intercept_[0])/w[1]

#根据超平面，找到超平面的两条边界线
b = svc.support_vectors_[0]
yy_down = a * xx + (b[1]-a*b[0])
b = svc.support_vectors_[-1]
yy_up = a * xx + (b[1]-a*b[0])

#绘制超平面和边界线
#(1)绘制样本点的散点图
sns.lmplot(data=data,x='Sugar',y='Butter',hue='CakeType',palette='Set1',fit_reg=False,scatter_kws={'s':150})
#（2）向散点图添加超平面
from matplotlib import pyplot as plt
plt.plot(xx,yy,linewidth=4,color='black')

#（3）向散点图添加边界线
plt.plot(xx,yy_down,linewidth=2,color='blue',linestyle='--')
plt.plot(xx,yy_up,linewidth=2,color='blue',linestyle='--')

效果如下：