珂朵莉树学习笔记

优质资源分享

学习路线指引（点击解锁）	知识定位	人群定位
Python实战微信订餐小程序	进阶级	本课程是python flask+微信小程序的完美结合，从项目搭建到腾讯云部署上线，打造一个全栈订餐系统。
Python量化交易实战	入门级	手把手带你打造一个易扩展、更安全、效率更高的量化交易系统

0x00 前言

0x01 关于其命名

最开始出现在 Codeforces Round #449 (Div. 1) C题 上，这位珂学家在题解中用了一种玄学的数据结构解题，开始命名为 ODT树（Old Driver Tree，老司机树，以出题者的ID命名），后来普遍称为珂朵莉树。

0x02 能解决的问题

珂朵莉树用于解决含有区间平推操作（即将区间上的数全部变为一个数）的问题时卓有成效，在数据随机的情况下，用 set 实现复杂度为 O(N log log N)O(N \ log \ log \ N)，用链表实现复杂度为 O(N log N)O(N \ log \ N)，比同类问题其他算法更优。时间复杂度证明请移步这篇文章。

0x03 前置知识

• set 相关知识

0x10 正文

本文使用 Codeforces Round #449 (Div. 1) C题 作为例题讲解珂朵莉树。

0x11 题意

– 威廉…
– 怎么了？
– 瑟尼欧里斯好像出了什么问题…
– 我会看看的…

瑟尼欧里斯是一把由特殊护符按特定顺序排列组成的剑。
已经 500500 年过去了，现在剑的状态很差，所以威廉决定检查一下。
瑟尼欧里斯由 nn 片护符组成，威廉把它们排成一列，每个护符上有一个数字 aia_i。
为了保养它，威廉需要进行 mm 次操作。
这里有四种操作：

• 1 l r x1 \ l \ r \ x : 将区间 [l,r][l, r] 上的数加上 xx。
• 2 l r x2 \ l \ r \ x : 将区间 [l,r][l, r] 上的数全部变为 xx。
• 3 l r x3 \ l \ r \ x : 查询区间 [l,r][l, r] 的第 xx 大数。
• 4 l r x y4 \ l \ r \ x \ y : 查询区间 [l,r][l, r] 上的数的 xx 次方之和对 yy 取模的值。

本题输入较为特殊，输入格式如下：
一行四个整数，分别为 nn，mm，seedseed，vmaxvmax，前两个变量意义如题目所述，后两个变量用于生成随机数据，数据生成伪代码如下

def rnd():

    ret = seed
    seed = (seed * 7 + 13) mod 1000000007
    return ret

for i = 1 to n:

    a[i] = (rnd() mod vmax) + 1

for i = 1 to m:

    op = (rnd() mod 4) + 1
    l = (rnd() mod n) + 1
    r = (rnd() mod n) + 1

    if (l > r): 
         swap(l, r)

    if (op == 3):
        x = (rnd() mod (r - l + 1)) + 1
    else:
        x = (rnd() mod vmax) + 1

    if (op == 4):
        y = (rnd() mod vmax) + 1

0x12 珂朵莉树基本思路

由于数据随机，所以在区间平推操作中区间长度普遍不会太短，所以区间总个数不会太多，于是我们就考虑维护每一个这样连续的区间，区间中的数都相同。

0x13 结构体定义

用一个结构体来维护每一个区间的信息。

struct node {
	ll l, r; //区间左右端点
	mutable ll v; //区间单个元素值
	node(ll l, ll r, ll v) : l(l), r(r), v(v) {}
	bool operator< (const node &a) const { return l < a.l; }
};

在上述定义中有下面一点需要注意：

• 因为元素值并不是固定的，所以一定要用 mutabel 让元素值可变起来

0x14 初始化

#include
set tree;

这样你就得到了一颗啥也没有的珂朵莉树。

0x15 spilt操作

因为一个区间上的数不一定自始至终都是一样的，所以我们需要一个分割函数将区间分隔开，这就是 spilt 函数。
  这个操作是珂朵莉树的核心操作之一，此函数有一个参数，表示要分裂的位置，我们先看代码，再解释它的运作过程。

auto spilt(ll pos) {
	auto it = tree.lower\_bound(node(pos, 0, 0));
	if(it != tree.end( ) && it -> l == pos) return it;
	it--;
	ll l = it -> l, r = it -> r, v = it -> v;
	tree.erase(it);
	tree.insert(node(l, pos - 1, v));
	return tree.insert(node(pos, r, v)).first;
}

首先，我们要找到一个左端点大于等于 pospos 的区间，用一个迭代器指向它（注意，如果你使用的是c++11，auto 必须要换成 set::iterator），如果当前区间的左端点等于 pospos （并且这个区间要存在）那就说明当前区间不用分割，直接返回当前迭代器，否则就向前跳转到前一个区间，并将其分割为 [l,pos−1][l, pos - 1] 和 [pos,r][pos, r] 两个区间。

0x16 assgin操作

珂朵莉树的核心操作之二，也就是区间平推操作。
  有了 spilt 函数，我们的实现也简单了很多，依旧是对着代码解释。

void assgin(ll l, ll r, ll v) {
	auto end = spilt(r + 1), start = spilt(l);
	tree.erase(start, end);
	tree.insert(node(l, r, v));
}

实现思路没什么好讲的，无非就是断开需要赋值的区间，全部删除再加入一个新的区间，重点在 spilt 的顺序上。
  看上去貌似和顺序没什么关系，如果单从逻辑上看确实如此，但是如果从实现上去看就会发现问题。
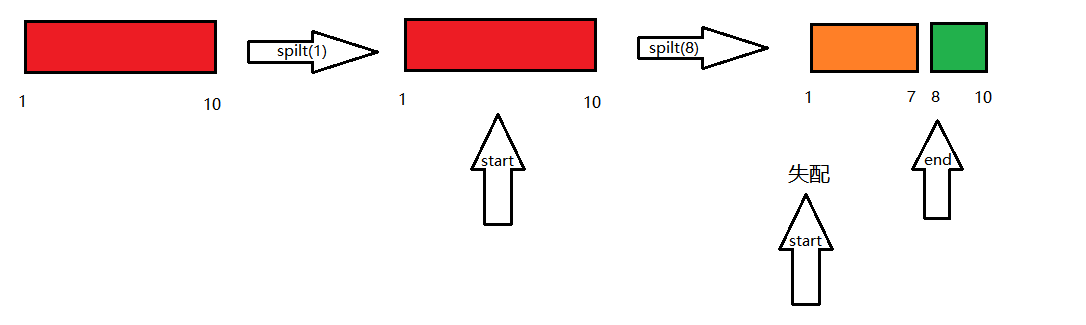
  假设我们要从区间 [1,10][1, 10] 里截取出 [3,7][3, 7]，我们先执行 spilt(1)，现在 start 迭代器指向的是区间 [3,10][3, 10]，然后我们再执行 spilt(8)，end 则指向了区间 [8，10][8，10]，此时我们发现 start 指向的迭代器被第二次 spilt 操作 erase 掉了，所以调用时可能会 RE。（之所以是可能，是因为这东西比较玄学，有可能一会 RE，一会 AC，为了避免这种麻烦，还是规范写法较为稳妥）
  如果还是不理解，就结合下图再多看几遍上一段。

0x17 其他代码实现

核心代码就上面两个，剩下的乱搞就行。

void add(ll l, ll r, ll x) { //区间加操作
	auto end = spilt(r + 1), start = spilt(l);
	for(auto it = start; it != end; it++)
		it -> v += x; //mulable的作用在此
} 

struct Rank {
	ll num, cnt; // 值与数量
	Rank(ll num, ll cnt) : num(num), cnt(cnt) {}
	bool operator< (const Rank &a) const { return num < a.num; }
};

ll get\_rank(ll l, ll r, ll x) { //求区间第 x 大数
	auto end = spilt(r + 1), start = spilt(l);
	vector vec;
 for(auto it = start; it != end; it++) vec.push\_back(Rank(it -> v, it -> r - it -> l + 1));
 sort(vec.begin( ), vec.end( )); //将区间上的所有数排序，以便后续暴力查找
 int i;
 for(i = 0; i < vec.size( ); i++) {
 if(vec[i].cnt < x) x -= vec[i].cnt;
 else break;
 }
 return vec[i].num;
}

ll get\_power(ll l, ll r, ll x, ll y) { //求区间 x 次方和 mod y 的值
	auto end = spilt(r + 1), start = spilt(l);
	ll ans = 0;
	for(auto it = start; it != end; it++) ans = (ans + power(it -> v, x, y) * (it -> r - it -> l + 1) % y) % y; //power 为快速幂函数
	return ans;
}

0x17 完整代码

请在确保自己理解上述所有内容的情况下阅读

#include
#include
#include
#include
#include
using namespace std;

typedef long long ll;
const int MOD = 1e9 + 7;
ll n, m, seed, vmax;

struct node {
	ll l, r;
	mutable ll v;
	node(ll l, ll r, ll v) : l(l), r(r), v(v) {}
	bool operator< (const node &a) const { return l < a.l; }
};

struct Rank {
	ll num, cnt;
	Rank(ll num, ll cnt) : num(num), cnt(cnt) {}
	bool operator< (const Rank &a) const { return num < a.num; }
};

set tree; 

ll rnd( );
auto split(ll pos);
void add(ll l, ll r, ll x);
ll power(ll a, ll b, ll p);
void assgin(ll l, ll r, ll v);
ll get\_rank(ll l, ll r, ll x);
ll get\_power(ll l, ll r, ll x, ll y);

int main( ) {
 cin >> n >> m >> seed >> vmax;
 for(int i = 1; i <= n; i++) tree.insert(node(i, i, rnd( ) % vmax + 1));
 for(int i = 1; i <= m; i++) {
 ll op, l, r, x, y;
 op = rnd( ) % 4 + 1;
 l = rnd( ) % n + 1;
 r = rnd( ) % n + 1;
 if(l > r) swap(l, r);
 if(op == 3) x = rnd( ) % (r - l + 1) + 1;
 else x = rnd( ) % vmax + 1;
 if(op == 4) y = rnd( ) % vmax + 1;
 
 if(op == 1) add(l, r, x);
 if(op == 2) assgin(l, r, x);
 if(op == 3) cout << get\_rank(l, r, x) << endl;
 if(op == 4) cout << get\_power(l, r, x, y) << endl;
 }
 return 0;
}

auto spilt(ll pos) {
 auto it = tree.lower\_bound(node(pos, 0, 0));
 if(it != tree.end( ) && it -> l == pos) return it;
 it--;
 ll l = it -> l, r = it -> r, v = it -> v;
 tree.erase(it);
 tree.insert(node(l, pos - 1, v));
 return tree.insert(node(pos, r, v)).first;
}

void assgin(ll l, ll r, ll v) {
 auto end = spilt(r + 1), start = spilt(l);
 tree.erase(start, end);
 tree.insert(node(l, r, v));
}

void add(ll l, ll r, ll x) {
 auto end = spilt(r + 1), start = spilt(l);
 for(auto it = start; it != end; it++)
 it -> v += x;
} 

ll get\_rank(ll l, ll r, ll x) {
 auto end = spilt(r + 1), start = spilt(l);
 vector vec;
 for(auto it = start; it != end; it++) vec.push\_back(Rank(it -> v, it -> r - it -> l + 1));
 sort(vec.begin( ), vec.end( ));
 int i;
 for(i = 0; i < vec.size( ); i++) {
 if(vec[i].cnt < x) x -= vec[i].cnt;
 else break;
 }
 return vec[i].num;
}

ll get\_power(ll l, ll r, ll x, ll y) {
 auto end = spilt(r + 1), start = spilt(l);
 ll ans = 0;
 for(auto it = start; it != end; it++) ans = (ans + power(it -> v, x, y) * (it -> r - it -> l + 1) % y) % y;
 return ans;
}

ll power(ll a, ll b, ll p) {
 ll res = 1, base = a % p;
 while(b) {
 if(b & 1) res = (res * base) % p;
 base = (base * base) % p;
 b >>= 1;
 }
 return res;
}

ll rnd( ) {
 ll res = seed;
 seed = (seed * 7 + 13) % MOD;
 return res;
}

0x18 小结

珂朵莉树的核心其实就二十行左右的代码，并不是什么很难的算法，但是由于其对于数据的要求，很少有题将其作为正解，但是考场骗分还是很有用的。

0x19 习题

• CF915E Physical Education Lessons
• P4344 [SHOI2015]脑洞治疗仪
• P3740 [HAOI2014]贴海报
• P4979 矿洞：坍塌
• CF343D Water Tree（涉及到树链剖分）

0x20 后记

本文是本蒟蒻近期学习了珂朵莉树，为了巩固所以写下了这篇学习笔记，如果有纰漏请指出。
  另外感谢本文用到的所有资料的提供者。
  还有，珂朵莉太可爱了~