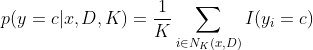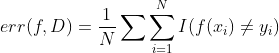MLAPP(翻译)—第一章
- 1 什么是机器学习
我们沉浸在信息中,渴望知识。—约翰奈斯比特。
我们正在进入大数据时代。例如,大约有1万亿个网页;每秒钟有一小时的视频上传到youtube上,每天的内容相当于10年的总和;1000多人的基因组,每一个都有![]() 个碱基对,已被各种实验室测序;沃尔玛每小时处理超过100万笔交易,并且包含超过2.5千兆字节(
个碱基对,已被各种实验室测序;沃尔玛每小时处理超过100万笔交易,并且包含超过2.5千兆字节(![]() )信息的数据库(Cukier 2010)等等。
)信息的数据库(Cukier 2010)等等。
这种大量的数据需要自动化的数据分析方法,这就是机器学习所提供的。特别是,我们将机器学习定义为一套可以自动检测数据中的模式,然后使用未发现的模式预测未来数据,或在不确定的情况下执行其他类型的决策(例如计划如何收集更多数据)。
本书认为解决这些问题的最好办法是使用概率论工具。概率论可以应用于任何涉及不确定性的问题。在机器学习中,不确定性有多种形式:给定一些历史数据如何做最好的预测?解释一些数据什么模型最好?执行下一步应该用什么测量等。机器学习的概率方法与统计领域相似,但在重点和术语方面略有不同。
我们将描述各种各样的概率模型,适用于各种各样数据和任务。我们还将描述各种学习和使用此类模型的算法。我们的目标不是开发一本专门技术的烹饪书,而是呈现一个统一的通过概率建模和推理的视角来观察这个领域。尽管我们会注意计算效率,但是关于如何将这些方法扩展到真正的海量数据集的细节在其他书籍中有更好的描述,如(Rajaraman and Ullman 2011; Bekkermanet al. 2011)
然而,应该注意的是,即使一个人有一个明显巨大的数据集,对于某些感兴趣的情况,数据点的有效数量可能非常少。实际上,跨越各种域的数据表现出称为长尾的属性,这意味着一些事物(例如,单词)非常常见,但大多数事物都非常罕见(见第2.4.6节详细信息)。例如,每天有20%的谷歌搜索从未出现过。这个意味着我们在本书中讨论的核心统计问题,涉及到从相对较小的样本量中归纳,仍然是非常重要,即使在大数据时代。
- 1.1 机器学习的分类
机器学习通常分为两种主要类型。在预测或监督学习方法,目标是学习一种映射从输入x到输出y,在给定输入输出对标签![]() ,这里D被叫为训练集,N是训练样本数量。在最简单的设置中,每个训练输入
,这里D被叫为训练集,N是训练样本数量。在最简单的设置中,每个训练输入![]() 用数值的D维向量表示,比如说,一个人的身高和体重。这些被叫特征,属性或者协变量。然而,一般来说,
用数值的D维向量表示,比如说,一个人的身高和体重。这些被叫特征,属性或者协变量。然而,一般来说,![]() 可以是一个复杂的结构化对象,例如图像,句子,电子邮件消息,时间序列,分子形状,图形等。
可以是一个复杂的结构化对象,例如图像,句子,电子邮件消息,时间序列,分子形状,图形等。
同样,输出或反应变量的形式原则上可以是任何形式,但是大多数方法都假定![]() 是来自某个有限集的分类或定类变量,
是来自某个有限集的分类或定类变量,![]() (如男性或女性),或者
(如男性或女性),或者![]() 是一个实值的标量(如收入水平)。当是
是一个实值的标量(如收入水平)。当是![]() 分类时,问题被称为分类或模式识别,当
分类时,问题被称为分类或模式识别,当![]() 是实值时,这个问题被称为回归,另一种变体,被称为序数回归,出现在标签空间y具有一些自然顺序的地方,例如等级a-f。
是实值时,这个问题被称为回归,另一种变体,被称为序数回归,出现在标签空间y具有一些自然顺序的地方,例如等级a-f。
机器学习的第二种主要类型是描述性的或无监督的学习方法。这里我们只给出给定的输入,![]() ,目标是在数据中找到“有趣模式”。这是一个很少被明确定义的问题,因为我们没有被告知需要寻找什么样的模式,并且没有明显的误差度量标准可供使用(与监督学习不同,我们可以将给定x的y预测与观察值进行比较)。
,目标是在数据中找到“有趣模式”。这是一个很少被明确定义的问题,因为我们没有被告知需要寻找什么样的模式,并且没有明显的误差度量标准可供使用(与监督学习不同,我们可以将给定x的y预测与观察值进行比较)。
还有第三种类型的机器学习,称为强化学习,这种学习很少被使用。 这对于如何学习行动或行为是很有用,当给定偶尔的奖励或惩罚信号时。(例如,考虑婴儿如何学会走路)不幸的是,RL超出了本书的范围,尽管我们确实在第5.7节中讨论RL的基础决策理论。参见例如(Kaelbling et al. 1996; Sutton and Barto 1998;Russell and Norvig 2010; Szepesvari 2010; Wiering and van Otterlo 2012)了解更多信息关于RL。
 (a)
(a)  (b)
(b)
图1.1左:一些彩色形状的标记训练示例,以及3个未标记的测试用例。右:将训练数据表示为N×D设计矩阵。行i代表特征向量![]() 。最后一列是标签,
。最后一列是标签,![]() 。根据Leslie Kaelbling的一个数字。
。根据Leslie Kaelbling的一个数字。
- 2 监督学习
我们从讨论监督学习开始对机器学习的研究,这是在实践中最广泛使用的ML形式。
- 2.1 分类
在本节中,我们将讨论分类。这里的目标是学习从输入x到输出y的映射,其中![]() ,其中c是类的数目。如果c=2,这被称为二分类(在这种情况下,我们通常假设
,其中c是类的数目。如果c=2,这被称为二分类(在这种情况下,我们通常假设![]() );如果c>2,这被称为多类分类。如果类标签不是互斥的(例如,某人可能被分类为高的和强壮的),我们将其称为多标签分类,但最好将其视为预测多个相关的二分类标签(所谓的多输出模型)。当我们使用术语“分类”时,我们将指具有单个输出的多类分类,除非我们另有说明。
);如果c>2,这被称为多类分类。如果类标签不是互斥的(例如,某人可能被分类为高的和强壮的),我们将其称为多标签分类,但最好将其视为预测多个相关的二分类标签(所谓的多输出模型)。当我们使用术语“分类”时,我们将指具有单个输出的多类分类,除非我们另有说明。
将问题形式化的一种方法是函数逼近。对于一些未知的函数f,我们假设![]() ,学习的目的是估计函数f在给定一个标记训练集上,然后使用
,学习的目的是估计函数f在给定一个标记训练集上,然后使用![]() 进行预测。(我们用帽子符号表示一个估计)我们的主要目标是对新输入进行预测,这意味着我们以前没有见过(这称为泛化),因为预测训练集上的输出很容易(我们只需查找答案)。
进行预测。(我们用帽子符号表示一个估计)我们的主要目标是对新输入进行预测,这意味着我们以前没有见过(这称为泛化),因为预测训练集上的输出很容易(我们只需查找答案)。
- 2.1.1 例子
作为分类的简单玩具示例,请考虑图中1.1(a)所示的问题。 我们有两类对象,分别对应标签0和1。输入是彩色形状。 这些已由一组D特征或属性描述,这些特征或属性存储在N×D设计矩阵X中,如图1.1(b)所示。 输入特征x可以是离散的,连续的或两者的组合。 除了输入之外,我们还有一个训练标签y的向量。
在图1.1中,测试用例是蓝色新月形,黄色圆形和蓝色箭头。 以前都没有见过这些。 因此,我们需要在训练集之外进行概括。一个合理的猜测是蓝色新月应该是y = 1,因为所有蓝色形状在训练集中都标记为1。 黄色圆圈是难分类,因为一些黄色的东西被标记为y = 1而一些被标记为y = 0,并且一些圆圈被标记为y = 1一些y = 0。因此,在黄色圆圈的情况下,不清楚正确的标签应该是什么。 同样,蓝色箭头的正确标签也不清楚。
- 2.1.2 概率预测的必要
要处理不明确的情况,如上面的黄色圆圈,需要返回一个概率。假定读者已经对概率的基本概念有了一些熟悉。如果没有,有必要,请参阅第2章进行复习。
在给定输入向量x和训练集D,我们将通过表示可能标签上的概率分布。通常,这表示长度为C的向量。(如果只有两个类,只返回单个![]() 就足够了,因为p(y = 1 | x,D)+ p(y =0 | x,D)= 1)在我们的符号中,我们明确表示概率是在测试输入x和训练集d上,将这些条件放在竖线的右侧。我们也在隐式地调节我们用来做预测模型的形式。在选择不同的模型时,我们将通过写p(y| x,d,m)来明确这个假设,其中m表示模型。但是,如果模型在上下文中是清晰的,为了简洁起见,我们将从符号中去掉m。
就足够了,因为p(y = 1 | x,D)+ p(y =0 | x,D)= 1)在我们的符号中,我们明确表示概率是在测试输入x和训练集d上,将这些条件放在竖线的右侧。我们也在隐式地调节我们用来做预测模型的形式。在选择不同的模型时,我们将通过写p(y| x,d,m)来明确这个假设,其中m表示模型。但是,如果模型在上下文中是清晰的,为了简洁起见,我们将从符号中去掉m。
给定概率输出,我们总是能够使用“真实标签”来计算我们的“最佳猜测”
![]()
这对应于最可能的类标签,被称为分布p(y| x,d)的模式;它也被称为map估计(map代表最大后验概率)。使用最可能的标签是直观的,但是我们将在第5.7节中给出这个过程更正式的理由。
现在考虑一个例子,例如黄色圆圈,其中![]() 远离1.0。在这种情况下,我们对自己的答案不是很有信心,所以最好说“我不知道”,而不是返回一个我们并不真正信任的答案。正如我们在第5.7节中所解释的,这在医学和金融等我们可能会规避风险的领域尤为重要。评估风险很重要的另一个应用程序是在播放电视游戏节目时,例如jeopardy。在这个游戏中,参赛者必须解决各种字谜和回答各种琐碎的问题,但如果回答错误,他们就会赔钱。2011年,ibm推出了一款名为watson的计算机系统,它击败了人类最危险的冠军。Watson使用了各种有趣的技术(Ferrucci等人,但就我们目前的目的而言,最相关的是它包含了一个模块,可以估计它对自己的答案有多自信。系统只有在充分确信答案是正确的情况下才会选择“嗡嗡”作响。类似地,谷歌也有一个名为smartass(广告选择系统)的系统,它可以根据你的搜索历史和其他用户、广告特定功能预测你点击广告的概率(metz 2010)。这种可能性被称为点击率或CTR,,可用于最大化预期利润。我们将在本书后面讨论系统背后的一些基本原则,比如smartass。
远离1.0。在这种情况下,我们对自己的答案不是很有信心,所以最好说“我不知道”,而不是返回一个我们并不真正信任的答案。正如我们在第5.7节中所解释的,这在医学和金融等我们可能会规避风险的领域尤为重要。评估风险很重要的另一个应用程序是在播放电视游戏节目时,例如jeopardy。在这个游戏中,参赛者必须解决各种字谜和回答各种琐碎的问题,但如果回答错误,他们就会赔钱。2011年,ibm推出了一款名为watson的计算机系统,它击败了人类最危险的冠军。Watson使用了各种有趣的技术(Ferrucci等人,但就我们目前的目的而言,最相关的是它包含了一个模块,可以估计它对自己的答案有多自信。系统只有在充分确信答案是正确的情况下才会选择“嗡嗡”作响。类似地,谷歌也有一个名为smartass(广告选择系统)的系统,它可以根据你的搜索历史和其他用户、广告特定功能预测你点击广告的概率(metz 2010)。这种可能性被称为点击率或CTR,,可用于最大化预期利润。我们将在本书后面讨论系统背后的一些基本原则,比如smartass。
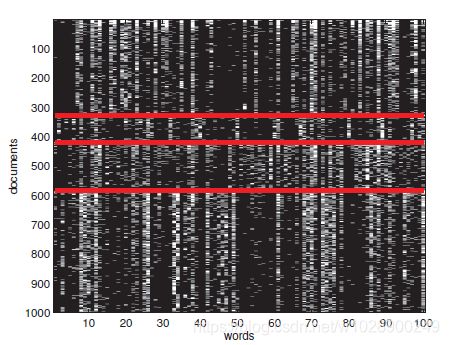
图1.2 20个新闻组数据中16242 x 100大小的子集。为了清楚起见,我们只显示1000行每一行是一个文档(表示为词袋模型字位向量),每一列是一个字。红线分隔了4个类,它们是(按降序排列的)comp、rec、sci、talk(这些是usenet组的标题)我们可以看到有一些词的子集,它们的存在或不存在都表示这个类。数据来自http://cs.nyu.edu/~roweis/data.html.NewsGroupsVisualize生成的图
1.2.1.3 真实世界的应用
分类可能是最广泛使用的机器学习形式,并已被使用来解决许多有趣的、通常很困难的现实问题。我们已经提到了一些重要的应用。下面我们再举几个例子。
文档分类和垃圾邮件过滤
在文档分类中,目标是对文档进行分类,例如网页或电子邮件消息,分为C类之一,即计算p(y = c | x,D),其中x是某些的文本表示。 一个特例是垃圾邮件过滤,其中的类是垃圾邮件y = 1或y = 0。
大多数分类器假设输入向量x的大小是固定的。用特征向量方式表示可变长度文档的一种常见方法是使用词袋表示法。这在第3.4.4.1节中有详细的解释,但基本思想是定义![]() iff单词j在文档i中发生。如果我们将此转换应用于我们数据集中的每个文档,我们将得到二进制文档×词共现矩阵:示例见图1.2。本质上,文档分类问题已经简化为寻找位的模式。例如,我们可能会注意到大多数垃圾邮件很可能包含“买”,“便宜”,“伟哥”等字样。在练习8.1和练习8.2中,您将获得将各种分类技术应用于垃圾邮件过滤问题的实践经验。
iff单词j在文档i中发生。如果我们将此转换应用于我们数据集中的每个文档,我们将得到二进制文档×词共现矩阵:示例见图1.2。本质上,文档分类问题已经简化为寻找位的模式。例如,我们可能会注意到大多数垃圾邮件很可能包含“买”,“便宜”,“伟哥”等字样。在练习8.1和练习8.2中,您将获得将各种分类技术应用于垃圾邮件过滤问题的实践经验。
 (a)
(a)
图1.3 鸢尾花的三种类型:山鸢尾,变色鸢尾和维吉尼亚鸢尾.来源:http://www.statlab.uni-heidelberg.de/data/iris/.在马丁·克拉姆和西娜的允许下使用
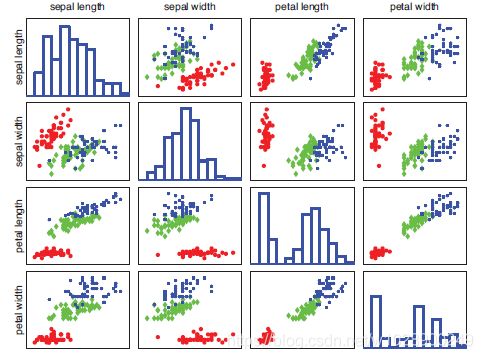
图1.4虹膜数据作为成对散点图的可视化。对角线绘制4个特征的边缘直方图。非对角线包含所有可能特征对的散点图。红圈=山鸢尾,绿钻石=变色鸢尾,蓝星=维吉尼亚鸢尾。Fisheririsdemo生成的图形
分类花
图1.3给出了另一个分类示例,由统计学家Ronald Fisher提供。目标是学会区分三种不同的鸢尾花,称为山鸢尾,变色鸢尾和维吉尼亚鸢尾。
 (a)
(a)  (b)
(b)
图1.5(a)前9个测试mnist灰度图像。(b)与(a)相同,但特征是随机排列的。两个版本的数据的分类性能相同(假设训练数据以相同的方式排列)。由ShuffledDigitsDemo生成的图。
幸运的是,植物学家没有直接处理图像,而是提取了4个有用的特征或特点:萼片的长度和宽度,以及花瓣的长度和宽度。(这种特征提取是一项重要而困难的任务。大多数机器学习方法使用一些人为选择的特性。稍后我们将讨论一些可以从数据中学习好特性的方法。)如果我们对鸢尾花数据做一个散点图,如图1.4所示,我们可以通过检查它们的花瓣长度或宽度是否低于某个阈值,很容易将山鸢尾(红色圆圈)与其他两类区分开来。然而,从维吉尼亚鸢尾中区分变色鸢尾,是稍微困难的;任何决定都需要基于至少两个特性(在应用机器学习方法之前,最好先进行探索性数据分析,例如绘制数据)。
图像分类与笔迹识别
现在考虑直接对图像进行分类的难题,人类没有对数据进行预处理。我们可能想要将图像整体分类,例如,它是室内还是室外场景? 它是水平还是垂直的照片? 它是否包含一只狗? 这称为图像分类。
在特殊情况下,图像由孤立的手写字母和数字组成,例如,在信件上的邮政编码或ZIP编码中,我们可以使用分类来执行手写识别。 在该领域中使用的标准数据集称为MNIST,其代表“Modified National Institute of Standards”。(使用“modified”一词是因为图像已经过预处理,以确保数字大部分位于图像的中心)该数据集包含60000个训练图像和10000个由不同的人编写的数字0到9的测试图像。图像大小为28×28,具有灰度范围为0:255的值。有关一些示例图像,请参见图1.5(a)。
许多通用分类方法忽略了输入特征中的任何结构,如空间布局。因此,它们也可以像图1.5(b)一样轻松地处理数据,这是相同的数据,只是我们随机排列了所有特性的顺序。(您将在练习1.1中验证这一点)这种灵活性既是一种幸事(因为方法是通用的)也是一种灾难(因为方法忽略了明显有用的信息源)。我们将在本书后面讨论如何在输入特性中开发结构。
(a)
图1.6人脸检测示例。(a)输入图像(墨菲家族,2010年8月5日摄)。经舍伍德工作室的伯纳德·迪德里奇允许使用。(b)分类器的输出,检测5个不同姿态的人脸。这是使用http://demo.PITTPAT.COM/在线演示程序制作的。分类器在人脸和非人脸的手工标记图像的1000s上进行训练,然后应用于测试图像中的密集重叠块。仅返回包含面部的概率足够高的补丁。经pittpatt.com允许使用
人脸检测与识别
一个比较困难的问题是在图像中查找目标;这称为目标检测或目标定位。一个重要的特殊情况是人脸检测。解决这个问题的一种方法是将图像分成多个位于不同位置、比例和方向的小重叠块,并根据每个重叠块是否包含面部特征对其进行分类。这被称为滑动窗探测器。然后系统返回人脸概率足够高的位置,示例见图1.6。这种人脸检测系统内置于大多数现代数码相机中,检测到的人脸的位置是用于确定自动对焦的中心。另一个应用程序是在谷歌街景系统中自动模糊人脸。
找到人脸后,可以继续进行人脸识别,这意味着估计此人的身份(见图1.10(a))。在这种情况下,类标签的数量可能非常大。此外,人们应该使用的特征可能与人脸检测问题中的特征不同。对于识别来说,诸如发型之类的面部细微差别可能对确定身份很重要,但对于检测来说,重要是对这些细节保持不变,并且仅关注面部和非面部的差别。有关视觉对象检测的更多信息,请参阅例如(Szeliski 2010)。
- 2.2 回归
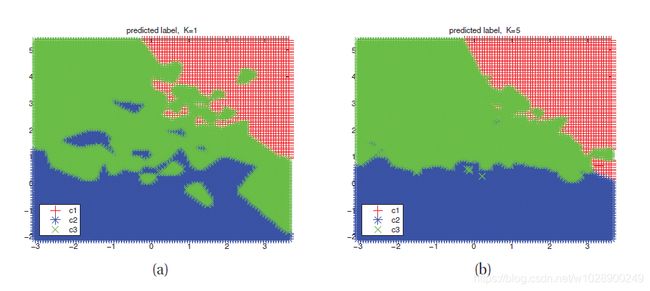
回归就像分类一样,除了反应变量是连续的。 图1.7显示了一个简单的例子:我们有一个实值输入![]() 和一个实值输出
和一个实值输出![]() 。我们考虑将两个模型拟合到数据中:直线和二次函数(我们将在下面解释如何适合这样的模型)。这一基本问题的各种扩展可能会出现,例如具有高维输入、异常值、非平稳响应等。我们将在本书后面讨论处理此类问题的方法。
。我们考虑将两个模型拟合到数据中:直线和二次函数(我们将在下面解释如何适合这样的模型)。这一基本问题的各种扩展可能会出现,例如具有高维输入、异常值、非平稳响应等。我们将在本书后面讨论处理此类问题的方法。
 (a)
(a) 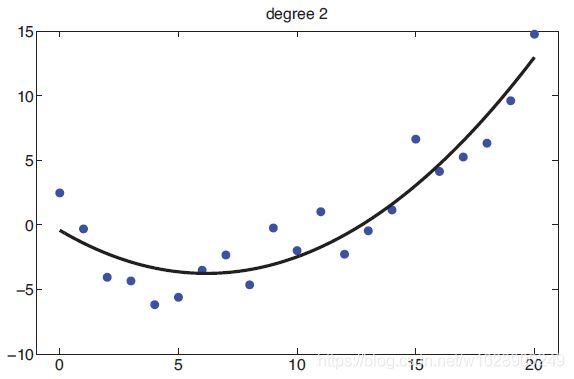 (b)
(b)
图1.7(a)一些一维数据的线性回归。(b)多项式回归的相同数据(次数2)。由linregpolyvsdegree生成的图形
下面是一些实际回归问题的例子
根据当前市场状况和其他可能的侧面信息,预测明天的股票市场价格。
预测在YouTube上观看给定视频的观众的年龄。
预测机器人手臂末端执行器在3D空间中的位置,给定发送到其各个电机的控制信号(扭矩)。
预测体内前列腺特异性抗原(PSA)的量作为多种不同临床测量的函数。
利用天气数据、时间、门传感器等预测建筑物内任何位置的温度。
- 3 无监督学习
我们现在考虑无监督学习,我们只给出输出数据,没有任何输入。目标是发现数据中的“有趣结构”,这有时被称为知识发现。与监督学习不同,我们不知道每个输入的期望输出是什么。相反,我们将我们的任务形式化为密度估计,也就是说,我们要建立形式![]() 的模型。与监督学习情况有两个不同之处。首先,我们用
的模型。与监督学习情况有两个不同之处。首先,我们用 ![]() 代替
代替![]() ,也就是说,有监督学习是条件密度估计,而无监督学习是无条件密度估计。第二,
,也就是说,有监督学习是条件密度估计,而无监督学习是无条件密度估计。第二,![]() 是特征向量,所以我们需要创建多元概率模型。相比之下,在有监督的学习中,
是特征向量,所以我们需要创建多元概率模型。相比之下,在有监督的学习中,![]() 通常只是我们试图预测的一个单一变量。这意味着对于大多数有监督的学习问题,我们可以使用单变量概率模型(具有与输入相关的参数),这大大简化了问题。我们将在第19章中讨论多输出分类,我们将看到它也涉及多变量概率模型。
通常只是我们试图预测的一个单一变量。这意味着对于大多数有监督的学习问题,我们可以使用单变量概率模型(具有与输入相关的参数),这大大简化了问题。我们将在第19章中讨论多输出分类,我们将看到它也涉及多变量概率模型。
无监督学习可以说是人类和动物学习中比较典型的一种。它也比监督学习更广泛地应用,因为它不需要一个人类专家手动标记数据。标记的数据不仅获取成本高昂,而且还包含信息相对较少,当然不足以可靠地估计复杂模型的参数。多伦多大学医学硕士的著名教授杰夫辛顿说:
当我们学会看的时候,没有人告诉我们正确的答案是什么——我们只是看看。你妈妈经常说
“那是条狗”,但信息很少。如果你能以这种方式获得一些信息,即使是每秒一点,那你就太幸运了。大脑的视觉系统有![]() 个神经连接。你只能活
个神经连接。你只能活![]() 秒。所以每秒钟学习一个比特是没有用的。你需要更多像
秒。所以每秒钟学习一个比特是没有用的。你需要更多像![]() 比特每秒。只有一个地方你能得到这么多信息:从输入本身。----杰弗里·辛顿,1996年(引用于(Gorder 2006年))。
比特每秒。只有一个地方你能得到这么多信息:从输入本身。----杰弗里·辛顿,1996年(引用于(Gorder 2006年))。
下面我们描述一些无监督学习的典型例子
- 3.1 发现集群
 (a)
(a)  (b)
(b)
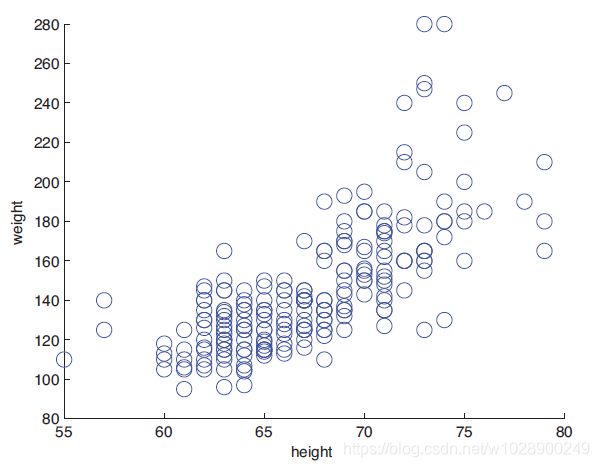
图1.8(a)一些人的身高和体重。(b)使用k=2个聚类的可能聚类。由kmeansheightweight生成的数字。
作为无监督学习的典型例子,考虑将数据分组的问题。例如,图1.8(a)绘制了一些二维数据,表示一组210人的身高和体重。看起来可能有不同的集群或子群,尽管不清楚有多少。让k表示簇的数目,我们的第一个目标是估计集群数量![]() 上的分布,这告诉我们数据中是否有子种群。为了简单起见,我们通常用它的模式近似
上的分布,这告诉我们数据中是否有子种群。为了简单起见,我们通常用它的模式近似![]() 的分布,
的分布,![]() 。在监督的情况下,我们被告知有两个类(男性和女性),但在在无监督的情况下,我们可以自由选择我们喜欢的多个或几个集群。选择“正确”复杂性的模型称为模型选择,并将在下面详细讨论。我们的第二个目标是估计每个点属于哪个簇,让
。在监督的情况下,我们被告知有两个类(男性和女性),但在在无监督的情况下,我们可以自由选择我们喜欢的多个或几个集群。选择“正确”复杂性的模型称为模型选择,并将在下面详细讨论。我们的第二个目标是估计每个点属于哪个簇,让![]() 表示为其分配数据点i的集群,
表示为其分配数据点i的集群,![]() 是一个隐藏或潜在变量的例子,因为它在训练集中从未被观察到,通过计算
是一个隐藏或潜在变量的例子,因为它在训练集中从未被观察到,通过计算![]() 。可以推断出每个数据点属于哪个簇。如图1.8(b)所示,假设k=2,我们使用不同的颜色来表示赋值。在这本书中,我们关注基于模型的聚类,这意味着我们将概率模型拟合到数据中,而不是运行一些特殊的算法。基于模型的方法的优点是可以客观地比较不同类型的模型(根据它们分配给数据的可能性),我们可以将它们组合成更大的系统,等等。
。可以推断出每个数据点属于哪个簇。如图1.8(b)所示,假设k=2,我们使用不同的颜色来表示赋值。在这本书中,我们关注基于模型的聚类,这意味着我们将概率模型拟合到数据中,而不是运行一些特殊的算法。基于模型的方法的优点是可以客观地比较不同类型的模型(根据它们分配给数据的可能性),我们可以将它们组合成更大的系统,等等。
下面是聚类的一些实际应用。
在天文学中,自动分类系统(Cheeseman等人1988年)发现了一种新型恒星,基于聚类天体物理测量。在电子商务中,通常根据用户的购买或上网行为将用户分组,然后向每个组发送定制的有针对性的广告(参见例如(Berkhin 2006))。
- 3.2 发现潜在因素
在处理高维数据时,通常通过将数据投影到一个低维子空间,来捕获数据的“本质”。
 (b)
(b)
图1.9(a)一组点,位于嵌入3d的2d线性子空间上。实心红线是第一主分量方向。黑色虚线是第二个PC方向。(b)数据的二维表示。由pcademo3d生成的图形。
 (a)
(a)  (b)
(b)
图1.10(a)25从Olivetti人脸数据库中随机选择64×64像素图像。(b)平均值和前三个主分量基向量(特征面)。
这叫做降维。一个简单的例子如图1.9所示,其中将一些三维数据投影到二维平面。二维近似相当好,因为大多数点靠近这个子空间。减少到1d将涉及将点投影到图1.9(a)中的红线上,这是一个相当差的近似值(我们将在第12章中阐明这一概念)。这种技术背后的动机是,尽管数据可能看起来很高维度,但可能只有少量的可变度,与潜在因素相对应。例如,在对人脸图像的外貌进行建模时,可能只有一些潜在的因素可以描述大多数的变化,例如灯光、姿势、身份等如图1.10所示。
当被用作其他统计模型的输入时,这种低维的表示通常会产生更好的预测精度,因为它们关注对象的“本质”,过滤掉不重要的特征。此外,低维表示对于实现快速近邻搜索非常有用,而二维投影对于可视化高维数据非常有用。
最常见的降维方法称为主成分分析(pca)。这可以被认为是(多输出)线性回归的无监督版本,在这里我们观察高维输出y,而不是低维“原因”z。因此,模型具有z→y的形式,我们必须“反转箭头”,从观测到的高维y推断出潜在的低维z。详情见第12.1节。
降维,特别是主成分分析,已经被应用于许多不同的领域。一些例子包括:
在生物学中,通常使用主成分分析来解释基因微阵列数据,以解释每个测量通常是许多基因的结果,这些基因通过它们属于不同生物途径的事实而在它们的行为中相关。
在自然语言处理中,通常使用称为潜在语义分析的pca变体进行文档检索(见第27.2.2节)。
在信号处理(例如,声音或神经信号)中,通常使用ica(pca的一种变体)将信号分离成不同的信号源(见第12.6节)。
在计算机图形学中,通常将运动捕捉数据投影到低维空间,并使用它创建动画。解决此类问题的方法见第15.5节。
图1.11使用图形套索(第26.7.2节)学习的稀疏无向高斯图形模型应用于一些流式细胞术数据(来自Sachs等人,它测量了11种蛋白质的磷酸化状态。
- 3.3 发现图结构
有时我们测量一组相关变量,我们想发现哪些变量与哪些其他变量最相关。这可以用一个图g来表示,其中的节点表示变量,边表示变量之间的直接依赖关系(当我们讨论图形模型时,我们将在第10章中详细说明这一点)。然后我们可以从数据中学习这个图形结构,即我们计算![]() 。
。
与一般的无监督学习一样,稀疏图的学习主要有两种应用:发现新知识和获得更好的联合概率密度估计。我们现在分别举几个例子
学习稀疏图形模型的大部分动机来自系统生物学社区。例如,假设我们测量细胞中某些蛋白质的磷酸化状态(Sachs等人,2005)。图1.11给出了从这些数据中学习到的图形结构的示例(使用第26.7.2节中讨论的方法)。另一个例子是,Smith等人(2006)研究表明,可以从时间序列的脑电数据中恢复某种鸟类的神经“接线图”。恢复的结构与鸟脑这一部分已知的功能连接紧密匹配。
在某些情况下,我们对解释图结构不感兴趣,我们只是想用它来建立相关性模型并进行预测。这方面的一个例子是在金融投资组合管理中,对大量不同股票之间协方差的精确模型非常重要。Carvalho和West(2007)表明,通过学习稀疏图,然后将其作为交易策略的基础,有可能超越不利用稀疏图的方法(即,赚更多的钱)。另一个例子是预测高速公路上的交通堵塞,霍维茨等人,(2005)描述一个被称为jambayes的部署系统,用于预测西雅图地区的交通流量。使用图形模型进行预测,其结构是从数据中学习的。
 (a)
(a)  (b)
(b)
图1.12(a)用封堵器的噪声图像。(b)基于成对mrf模型的基本像素强度的估计。资料来源:图8(Felzenszwalb和Huttenlocher,2006年)。在佩德罗·费尔岑斯瓦布的允许下使用。
- 3.4 矩阵完成
有时我们会丢失数据,也就是说,值未知的变量。例如,我们可能进行了一项调查,有些人可能没有回答某些问题。或者我们可能有各种各样的传感器,其中一些失灵了。相应的设计矩阵中会有“洞”,这些缺失的条目通常用NaN表示,NaN代表“不是数字”。插补的目的是为缺失的条目推断合理的值。这有时被称为矩阵完成。下面我们给出一些应用实例。
- 3.4.1 图像修复
一个有趣的类似于插补的任务被称为图像修复。目标是在具有真实结构的图像中“填充”孔洞(例如,由于划痕或遮挡)。如图1.12所示,我们对图像进行去噪,并输入隐藏在遮挡后面的像素。这可以通过建立像素的联合概率模型来解决,给定一组干净的图像,然后在给定已知变量(像素)的情况下推断未知变量(像素)。这有点像masket-basket分析,只是数据是实值的,并且是空间结构的,所以我们使用的概率模型种类是完全不同的。一些可能的选择见第19.6.2.7和13.8.4节。
- 3.4.2 协同过滤
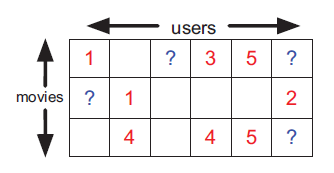
另一个类似于插补的任务的有趣例子是协作过滤。这方面的一个常见例子是,根据人们和其他人对已经看过的电影的评价,预测人们希望看哪些电影。关键的思想是,预测不是基于电影或用户的特征(尽管它可能是),而是仅仅基于评分矩阵。更准确地说,我们有一个矩阵x,其中x(m,u)是电影m的用户u的评分(比如1到5之间的整数,其中1表示不喜欢,5表示喜欢)。请注意,x中的大多数条目将丢失或未知,因为大多数用户不会对大多数电影进行分级。因此我们只观察x矩阵的一个很小的子集,我们希望预测一个不同的子集。特别是,对于任何给定的用户u,我们可能希望预测他/她最希望观看哪些未分级的电影。
图1.13电影分级数据示例。训练数据为红色,测试数据用?,空单元格未知。
为了鼓励这方面的研究,DVD租赁公司Netflix于2006年发起了一项竞赛,奖金100万美元(见http://netflix prize.com/)。特别是,他们提供了一个大的收视率矩阵,大小为1到5,用约50万用户创建的约18,000部电影。整个矩阵将有![]() 个条目,但只观察到约1%的条目,因此矩阵非常稀疏。其中一部分用于训练,其余部分用于测试,如图1.13所示。 竞争的目标是比Netflix现有系统更准确地预测。2009年9月21日,该奖项授予了一个名为“BellKor’s Pragmatic Chaos”的研究团队。 第27.6.2节讨论了他们的一些方法。有关团队及其方法的更多详细信息,请访问http://www.netflixprize.com/community/viewtopic.php?id=1537。
个条目,但只观察到约1%的条目,因此矩阵非常稀疏。其中一部分用于训练,其余部分用于测试,如图1.13所示。 竞争的目标是比Netflix现有系统更准确地预测。2009年9月21日,该奖项授予了一个名为“BellKor’s Pragmatic Chaos”的研究团队。 第27.6.2节讨论了他们的一些方法。有关团队及其方法的更多详细信息,请访问http://www.netflixprize.com/community/viewtopic.php?id=1537。
1.3.4.3 市场篮子分析
在商业数据挖掘中,人们对一个叫做市场篮子分析的任务非常感兴趣。数据由一个(通常很大但稀疏的)二进制矩阵组成,其中每一列表示一个项或产品,每一行表示一个事务。如果项目j是在第i次交易中购买的,我们![]() 将设置为1。许多商品都是一起购买的(如面包和黄油),因此它们之间会有关联。给定一个新的部分观测位向量,表示消费者购买的商品的子集,目标是预测哪些其他位可能打开,表示消费者可能购买的其他商品。(与协作过滤不同,我们通常假设训练数据中没有丢失数据,因为我们知道每个客户过去的购物行为)
将设置为1。许多商品都是一起购买的(如面包和黄油),因此它们之间会有关联。给定一个新的部分观测位向量,表示消费者购买的商品的子集,目标是预测哪些其他位可能打开,表示消费者可能购买的其他商品。(与协作过滤不同,我们通常假设训练数据中没有丢失数据,因为我们知道每个客户过去的购物行为)
除了建模采购模式之外,这项任务还出现在其他领域。例如,可以使用类似的技术来建模复杂软件系统中文件之间的依赖关系。在这种情况下,任务是在给定已更改的文件子集的情况下,预测需要更新哪些其他文件以确保一致性(参见,例如,hu等人,2010)
使用频繁项集挖掘(frequency itemset mining)来解决这类任务是很常见的,它会创建关联规则(参见例如haste等人,2009年,第14.2节)。或者,我们可以采用概率方法,并拟合联合密度模型![]() 到位向量,参见例如(hu等人2010)这类模型通常比关联规则具有更好的预测准确性,尽管它们可能不太容易解释。这是数据挖掘和机器学习之间的典型区别:在数据挖掘中,更强调可解释的模型,而在机器学习中,更强调精确的模型。
到位向量,参见例如(hu等人2010)这类模型通常比关联规则具有更好的预测准确性,尽管它们可能不太容易解释。这是数据挖掘和机器学习之间的典型区别:在数据挖掘中,更强调可解释的模型,而在机器学习中,更强调精确的模型。
 (a)
(a)
 (b)
(b)
图1.14(a)k=3时二维k近邻分类器的图解。测试点x1的3个最近邻具有标签1、1和0,因此我们预测p(y=1 x1,d,k=3)=2/3。测试点x2的3个最近邻具有0、0和0标签,因此我们预测p(y=1 x2,d,k=3)=0/3。(b)1-nn引起的voronoi镶嵌图解。根据图4.13(Duda等人2001)。
- 4 机器学习中的一些基本概念
在本节中,我们将介绍机器学习中的一些关键思想。我们将在本书的后面对这些概念进行扩展,但是我们将在这里简要介绍它们,以使我们对即将到来的事情有一个了解。
- 4.1 参数模型与非参数模型
在这本书中,我们将集中讨论![]() 或
或![]() 形式的概率模型,这取决于我们分别对有监督学习还是无监督学习感兴趣。定义此类模型的方法有很多,但最重要的区别是:模型是否有固定数量的参数,或者参数数量是否随着训练数据的数量而增长?前者称为参数模型,后者称为非参数模型。参数模型的优点是通常使用起来更快,但缺点是对数据分布的性质作出更强的假设。非参数模型更为灵活,但对于大型数据集来说,往往难以计算。我们将在下面的章节中给出这两种模型的示例。为了简单起见,我们将重点放在有监督的学习上,尽管我们的大部分讨论也适用于无监督的学习。
形式的概率模型,这取决于我们分别对有监督学习还是无监督学习感兴趣。定义此类模型的方法有很多,但最重要的区别是:模型是否有固定数量的参数,或者参数数量是否随着训练数据的数量而增长?前者称为参数模型,后者称为非参数模型。参数模型的优点是通常使用起来更快,但缺点是对数据分布的性质作出更强的假设。非参数模型更为灵活,但对于大型数据集来说,往往难以计算。我们将在下面的章节中给出这两种模型的示例。为了简单起见,我们将重点放在有监督的学习上,尽管我们的大部分讨论也适用于无监督的学习。
- 4.2 一种简单的非参数分类器:k近邻
非参数分类器的一个简单示例是K最近邻(KNN)分类器。这只是“查看”训练集中最接近测试输入x的k个点,计算每个类中有多少成员在这个集合中(k点集合),并返回该经验分数作为估计值,如图1.14所示。更正式一点
其中![]() 是x在D中的K个最近点,而
是x在D中的K个最近点,而![]() 是指示函数,定义如下:
是指示函数,定义如下:
这种方法是基于记忆的学习或基于实例的学习的一个例子。它可以从第14.7.3节中解释的概率框架中导出。最常用的距离度量是欧几里德距离(它限制了该技术对实值数据的适用性),尽管可以使用其他度量。
图1.15给出了一个实际方法的例子,其中输入是二维的,我们有三个类,k=10。(我们在下面讨论k的影响)面板(a)绘制了![]() 训练数据。 面板(b)绘制,其中x在点网格上评估。面板(c)绘制
训练数据。 面板(b)绘制,其中x在点网格上评估。面板(c)绘制![]() 。我们不需要绘制
。我们不需要绘制![]() ,因为概率等于1。面板(d)绘制地图估计值
,因为概率等于1。面板(d)绘制地图估计值![]() 。
。
K = 1的KNN分类器引起点的Voronoi曲面细分(见图1.14(b))。这是一个空间分区,它将区域![]() 与每个点关联起来,使得
与每个点关联起来,使得![]() 中的所有点都比任何其他点更接近于
中的所有点都比任何其他点更接近于![]() 。在每个单元格中,预测的标签是对应训练点的标签。
。在每个单元格中,预测的标签是对应训练点的标签。
图1.15(a)二维三类综合训练数据。(b)k=10时knn的一类概率。(c)二类概率。(d)类别标签的地图估计。
![]()
图1.16维度灾难图解。(a)我们在一个更大的单位立方体中嵌入一个S边的小立方体。(b)我们绘制一个立方体的边缘长度,以覆盖单位立方体的给定体积,作为维数的函数。根据图2.6(Haste等人2009)。
- 4.3 维度灾难
只要给出一个良好的距离度量,并有足够的标记训练数据,knn分类器就简单且能很好地工作。事实上,可以证明,如果n→∞(cover和hart 1967),knn分类器可以达到最佳性能的2倍之内。
然而,knn分类器的主要问题是它们不能很好地处理高维输入。在高维环境中表现不佳是由于维数灾难。
为了解释这个灾难,我们举了一些例子(Haste等人2009年,第22页)。考虑将knn分类器应用于输入均匀分布在d维单位立方体中的数据。假设我们通过在x周围“生长”一个超立方体来估计测试点x周围类标签的密度,直到它包含数据点的期望分数f。这个立方体的预期边长是![]() 。如果d=10,我们希望根据10%的数据进行估计,我们得到了
。如果d=10,我们希望根据10%的数据进行估计,我们得到了![]() ,因此我们需要将立方体沿着x周围的每个维度扩展80%。即使我们只使用1%的数据,我们也会发现
,因此我们需要将立方体沿着x周围的每个维度扩展80%。即使我们只使用1%的数据,我们也会发现![]() ,见图1.16。由于数据的整个范围在每个维度上只有1个,我们看到该方法不再是非常局部的,尽管它的名称是“最近的邻居”。观察距离如此之远的邻居的问题在于,它们可能不能很好地预测给定点上输入输出函数的行为。
,见图1.16。由于数据的整个范围在每个维度上只有1个,我们看到该方法不再是非常局部的,尽管它的名称是“最近的邻居”。观察距离如此之远的邻居的问题在于,它们可能不能很好地预测给定点上输入输出函数的行为。
![]()
图1.17(a)均值为0,方差为1的高斯分布函数。由gaussplotdemo生成的图形。(b)条件密度模型![]() 的可视化。当我们离开回归线时,密度以指数速度下降。
的可视化。当我们离开回归线时,密度以指数速度下降。
- 4.4 分类和回归的参数模型
对抗维数灾难的主要方法是对数据分布的性质作出一些假设(对于有监督问题![]() 或对于无监督问题
或对于无监督问题![]() )。这些假设被称为归纳偏差,通常以参数模型的形式体现,参数模型是一个具有固定参数数的统计模型。下面我们将简要介绍两个广泛使用的示例;我们将在本书后面更深入地讨论这些模型和其他模型。
)。这些假设被称为归纳偏差,通常以参数模型的形式体现,参数模型是一个具有固定参数数的统计模型。下面我们将简要介绍两个广泛使用的示例;我们将在本书后面更深入地讨论这些模型和其他模型。
- 4.5 线性回归
最广泛使用的回归模型之一是线性回归。这表明输出是输入的线性函数。这可以写成如下
其中,![]() 表示输入向量x和模型权重向量
表示输入向量x和模型权重向量![]() 之间的内积或标量积,
之间的内积或标量积,![]() 是线性预测和真实输出之间的残差。
是线性预测和真实输出之间的残差。
我们经常假设![]() 是高斯分布或正态分布。我们用
是高斯分布或正态分布。我们用![]() 表示,其中
表示,其中![]() 是平均值,
是平均值,![]() 是方差(详见第2章)。当我们绘制这个分布图时,我们得到如图1.17(a)所示的众所周知的钟形曲线。
是方差(详见第2章)。当我们绘制这个分布图时,我们得到如图1.17(a)所示的众所周知的钟形曲线。
为了使线性回归和高斯之间的连接更加明确,我们可以用以下形式重写模型:
![]()
这说明模型是一个条件概率密度。在最简单的情况下,我们假设![]() 是x的线性函数,所以
是x的线性函数,所以![]() ,并且噪声是固定的,
,并且噪声是固定的,![]() 。在这种情况下,
。在这种情况下,![]() 是模型的参数。
是模型的参数。
例如,假设输入为一维。 我们可以表示预期的输出如下:
![]()
其中![]() 是截距或偏差项,
是截距或偏差项,![]() 是斜率,这里我们定义了向量
是斜率,这里我们定义了向量![]() (在输入向量前加上常数1项是一种常见的符号技巧,它允许我们将截距项与模型中的其他项结合起来)。如果
(在输入向量前加上常数1项是一种常见的符号技巧,它允许我们将截距项与模型中的其他项结合起来)。如果![]() 为正,则意味着我们期望输出随着输入的增加而增加。这在图1.17(b)的1d中进行了说明;图1.7(a)中显示了平均输出与 x的更常规的曲线图。
为正,则意味着我们期望输出随着输入的增加而增加。这在图1.17(b)的1d中进行了说明;图1.7(a)中显示了平均输出与 x的更常规的曲线图。
线性回归可以通过用输入的非线性函数![]() 代替x来模拟非线性关系。也就是说,我们用
代替x来模拟非线性关系。也就是说,我们用
![]()
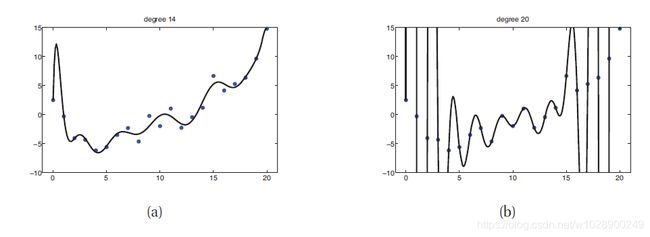
这称为基函数展开。例如,图1.18说明了![]() ,对d=14和d=20。这被称为多项式回归。我们将在本书后面考虑其他类型的基函数。事实上,许多流行的机器学习方法(如支持向量机、神经网络、分类和回归树等)可以被看作是从数据估计基函数的不同方式,正如我们在第14章和第16章中讨论的。
,对d=14和d=20。这被称为多项式回归。我们将在本书后面考虑其他类型的基函数。事实上,许多流行的机器学习方法(如支持向量机、神经网络、分类和回归树等)可以被看作是从数据估计基函数的不同方式,正如我们在第14章和第16章中讨论的。
图1.18 14度和20度多项式通过最小二乘法拟合到21个数据点
![]()
图1.19(a)sigmoid或logistic功能。我们有sigm(-∞)=0,sigm(0)=0.5,sigm(∞)=1。(b)SAT分数的逻辑回归。实心黑点是数据。开放的红色圆圈是预测的概率。绿色十字表示两个学生的SAT成绩相同,为525分(因此输入表示X相同),但训练标签不同(一个学生通过,Y=1,另一个失败,Y=0)。因此,仅使用sat特征并不能完全分离这些数据。
- 4.6 逻辑回归
我们可以通过两个改变将线性回归推广到(二元)分类设置,首先我们用伯努利分布代替y的高斯分布,这更适合于输出为二元![]() 的情况。也就是说,我们用
的情况。也就是说,我们用
![]()
其中![]() ,其次,我们像以前一样计算输入的线性组合,但是我们通过一个函数传递它,通过定义确保
,其次,我们像以前一样计算输入的线性组合,但是我们通过一个函数传递它,通过定义确保![]()
![]()
其中是指![]() 函数,也称为logistic或logit函数。 这被定义为
函数,也称为logistic或logit函数。 这被定义为
术语“sigmoid”是指S形,图1.19(a)为一个图。它也被称为挤压函数,因为它将整条实线映射到[0,1],这是将输出解释为概率所必需的。
把这两个步骤放在一起
![]()
这被称为逻辑回归,因为它与线性回归相似(尽管它是一种分类形式,而不是回归)。
图1.19(b)显示了逻辑回归的一个简单例子
![]()
其中![]() 是学生i和
是学生i和![]() 的
的![]() 分数,无论他们是否通过了课程。实心黑点显示训练数据,红色圆圈绘制
分数,无论他们是否通过了课程。实心黑点显示训练数据,红色圆圈绘制![]() ,其中
,其中![]() 是从训练数据估计的参数(我们在第8.3.4节中讨论了如何计算这些估计值)。
是从训练数据估计的参数(我们在第8.3.4节中讨论了如何计算这些估计值)。
如果我们将输出概率阈值设为0.5,我们就可以得到一个形式为
![]()
通过查看图1.19(b),我们看到![]() ,
,![]() 。我们可以想象在
。我们可以想象在![]() 处画一条垂直线;这就是所谓的决策边界。该垂直线左侧的所有内容都归为0,右侧的所有内容都归为1。
处画一条垂直线;这就是所谓的决策边界。该垂直线左侧的所有内容都归为0,右侧的所有内容都归为1。
我们注意到,即使在训练集上,此决策规则也具有非零错误率。这是因为数据不是线性可分的,也就是说,没有直线可以把0和1分开,我们可以用基函数展开来创建具有非线性决策边界的模型,就像非线性回归一样。我们将在本书后面看到许多这样的例子。
- 4.7 过度拟合
当我们拟合高度灵活的模型时,我们需要注意不要过度拟合数据,也就是说,我们应该避免尝试对输入中的每一个微小变化进行建模,因为这更可能是噪声而不是真实信号。这如图1.18(b)所示,在图中我们看到,使用高次多项式会导致曲线非常“摇摆”。真正的函数不太可能有如此极端的振荡。因此,使用这样一个模型可能会导致对未来产出的准确预测。
作为另一个例子,考虑knn分类器。k值对模型的行为有很大的影响。当k=1时,该方法在训练集上没有错误(因为我们只返回原始训练点的标签),但是得到的预测曲面非常“摇摆”(见图1.20(a))。因此,该方法在预测未来数据时可能效果不佳。在图1.20(b)中,我们看到使用k=5可以得到更平滑的预测曲面,因为我们在更大的邻域上求平均值。随着K增加时,预测变得更平滑,直到在K = N的极限中,我们最终预测整个数据集的多数标签。 下面我们讨论如何选择K的“正确”值。
- 4.8 模型选择
当我们有各种不同复杂度的模型(例如,具有不同程度多项式的线性或logistic回归模型,或具有不同k值的knn分类器)时,我们应该如何选择合适的模型?一种自然的方法是计算每种方法在训练集上的误分类率。定义如下:
其中![]() 是我们的分类器。在图1.21(a)中,我们绘制了一个KNN分类器的错误率与K的关系(蓝色虚线)。我们发现增加k会增加训练集上的错误率,因为我们过度平滑。如上所述,我们可以使用k=1在训练集上获得最小的错误,因为这个模型只是存储数据。
是我们的分类器。在图1.21(a)中,我们绘制了一个KNN分类器的错误率与K的关系(蓝色虚线)。我们发现增加k会增加训练集上的错误率,因为我们过度平滑。如上所述,我们可以使用k=1在训练集上获得最小的错误,因为这个模型只是存储数据。
图1.20基于图1.15(a)中数据的knn预测面。(a)k=1。(b)k=5。
然而,我们关心的是泛化误差,它是对未来数据进行平均时误分类率的期望值。(详见第6.3节)。这可以通过计算大型独立测试集上的错误分类率来近似,而不是在模型训练期间使用。我们在图1.21(a)中用实心红色(上部曲线)绘制测试误差与K的关系。现在我们看到一条U形曲线:对于复杂模型(小K),方法过拟合;对于简单模型(大K),方法欠拟合。因此,选择k的一个明显方法是在测试集上选择误差最小的值(在本例中,10到100之间的任何值都应该很好)。
不幸的是,在训练模型时,我们没有访问测试集的权限(通过假设),因此我们不能使用测试集来选择正确复杂度的模型。但是,我们可以通过将训练集分成两部分来创建测试集:用于训练模型的部分和第二部分,称为验证集,用于选择模型复杂性。然后,我们将所有模型都拟合到训练集上,并在验证集上评估它们的性能,然后选择最佳的模型。一旦我们选出了最好的,我们就可以把它改装成所有可用的数据。如果我们有一个单独的测试集,我们可以评估在这方面的性能,以估计我们的方法的准确性。(我们将在第6.5.3节中对此进行更详细的讨论。)
通常我们使用大约80%的数据用于训练集,20%用于验证集。但是,如果训练案例的数量很少,这种技术就会遇到问题,因为模型没有足够的数据进行训练,而且我们也没有足够的数据对未来的性能做出可靠的估计。
一个简单但流行的解决方案是使用交叉验证(cv)。这个想法很简单:我们将训练数据分成k个折叠;然后,对于每个折叠![]() ,我们以循环的方式在除k以外的所有折叠上进行训练,并在k上测试。如图1.21(b)所示。然后计算所有折叠的平均误差,并将其用作测试误差。(注意,每个点只预测一次,尽管它将用于训练k-1次)。通常使用k=5;这称为5-fold CV.。如果我们设置K = N,那么我们得到一个名为leave-one out cross validation或LOOCV的方法,因为在折叠i中,我们训练所有数据情况除了i,然后在i上测试。练习1.3要求您计算K和5-fold CV测试误差估计值,并将其与图1.21(a)中的经验测试误差进行比较。
,我们以循环的方式在除k以外的所有折叠上进行训练,并在k上测试。如图1.21(b)所示。然后计算所有折叠的平均误差,并将其用作测试误差。(注意,每个点只预测一次,尽管它将用于训练k-1次)。通常使用k=5;这称为5-fold CV.。如果我们设置K = N,那么我们得到一个名为leave-one out cross validation或LOOCV的方法,因为在折叠i中,我们训练所有数据情况除了i,然后在i上测试。练习1.3要求您计算K和5-fold CV测试误差估计值,并将其与图1.21(a)中的经验测试误差进行比较。
为knn分类器选择k是一个更为普遍的问题,即模型选择的特殊情况,在这个问题中,我们必须在具有不同灵活性的模型之间进行选择。交叉验证广泛用于解决此类问题,尽管我们将在本书后面讨论其他方法。
![]()
图1.21(a)k近邻分类器的误分类率与k的关系。在左边,k很小,模型很复杂,因此我们过拟合。在右边,k很大,模型很简单,我们欠拟合。蓝色虚线:训练集(大小200)。实心红线:测试集(大小500)。(b)5倍交叉验证示意图。
- 4.9 无免费午餐定理
所有的模型都是错误的,但是有些模型是有用的。-乔治·博克斯(Box and Draper 1987,第424页)
许多机器学习都涉及设计不同的模型,以及适合它们的不同算法。 我们可以使用交叉验证等方法来根据经验为我们的特定问题选择最佳方法。 然而,没有普遍最好的模型 - 这有时被称为无免费午餐定理(Wolpert 1996)。 这样做的原因是,在一个域中运行良好的一组假设在另一个域中可能效果不佳。
由于没有免费午餐定理,我们需要开发许多不同类型的模型,以涵盖现实世界中出现的各种各样的数据。 对于每个模型,我们可以使用许多不同的算法来训练模型,从而进行不同的速度 - 精度 - 复杂度权衡。 我们将在后续章节中研究这种数据,模型和算法的组合。