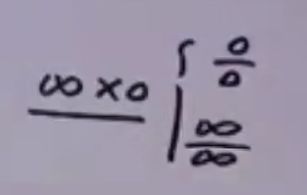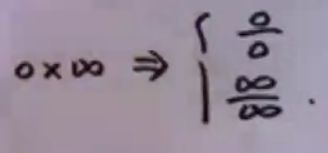第一章 极限与连续 （part1）极限

数学一定是一个先微观再宏观的过程，先弄清楚每一个细枝末节，然后才有调动一大块的资格。

极限定义

数列极限的定义，就是当n不停的往正无穷走的时候，这个数列不断向一个常数靠近，而且是无限地在靠，那么这个常数就叫做这个数列的极限。

这个符号表达的意思

• 趋于0，代表永远也达不到0，是可以这样认为的。

在那个点的极限和在那个点的函数值没有关系

在这个点的极限存在和在这个点的左极限和有极限存在且相等充分必要

再这种情况的时候一定要记得分左右极限去考虑

无穷小是0，无穷小的研究对象是一个函数，而且是在某种条件下才是无穷小的，除了0不带条件

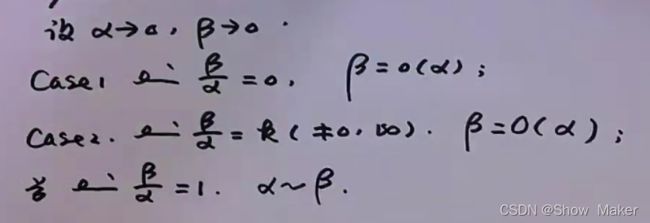
第一个是高阶无穷小
第二个是同阶无穷小
第三个是等价无穷小

极限性质

1.唯一性
极限如果有，那么只有一个

2.保号性
去心领域是一个这样的东西

右边的东西代表你邻域的半径，a代表你的心，x->0的话就是0，你的邻域就是左右两块

如果你的极限是大于0的，那么你一定能够找到一个去心邻域，在该邻域内，你的函数值是大于0的

如果你的极限是小于0的，那么你一定能够找到一个去心邻域，在该邻域内，你的函数值是小于0的

要根据题目给的式子去推断的，得这样才能推断出东西来。
推断得有足够的理由去推断
如果题目有说它的极限的保号性，那么你就得要考虑用一下极限的保号性
如果推出了题目给的数据比如说0，那么你就需要很敏感去替换了

有导数有极值点，需要考虑怎么样才能得出一个区间让导数的符号变换一下（去心邻域，保号性）

极限存在准则

准则一 夹逼定理

夹逼定理

有限的几个几次幂相加，记得要用夹逼定理：
放缩：左边是只留一个最大的，右边的全部改成最大的

这种又有x，又有n的，你看左边是研究n，所以是数列极限
直接可以应用那个结论，取三个中最大的为值，然后如果不知道谁是最大的，那么就需要分类讨论

这是先里面求和再极限

这种的缩放呢，把最小的放在左边，把最大的放在右边
然后全部加起来就是全部加起来，
直接夹逼定理拿下

在求极限的时候，同除以一个$n^2$这种操作应该算蛮常见的

分子或者分母，有一个不齐，赶紧夹逼定理
而且缩放的时候，放大或者缩小，齐的地方不能动，要动非齐的

先说明一个i的情况的大小关系，然后加起来，再次说明大小关系
然后分别求出小的和大的的值发现相等，然后就可以用夹逼定理了

当遇到分子的次数相等，分母的次数相等，并且分母的次数比分子多一次的情况下，用夹逼定理肯定错，这是标准的定积分的定义

牛顿莱布尼茨公式

遇到分子和分母的次数的齐的，然后分母的次数比分子的次数要多一次，就用定积分的公式。
就是得要凑出

这三种东西，然后直接就是定积分定义拿下了。

这三个东西一定要记牢啊

准则二 单调有界的数列必有极限

有界的定义，就如果你是单调递减的，那么你就考虑下界就可以了。

需要记的两个重要不等式

a1>0
推出有下界，并且下界等于0（一叶知秋，我有90%的把握）

证明极限存在：
1.有界-》数学归纳法
2.单调-》重要不等式
求极限：
设极限等于一个值，在你已有的等式呢，你把极限换上去，进入等式的一部分。然后你再去解。

如果说递增是显然的，那么你可以直接说显然递增
证明上界再次应用数学归纳法，a_k下界是一个东西，然后你只需要证明a_k+1的下界也是这个东西你就可以直接说a_k的上界就是你设的那个东西了。
递增加有上界-》根据极限存在准则得出极限存在
n趋于无穷大，n和n+1可以看作没区别，a_n和a_n+1也可以看作没区别

1.有界：重要不等式，一定要记住
2.相邻的两项相减a_n+1-a_n，得出结论之后再利用前面问的结论再次得出结论。得到单调递减

无穷小的性质

无穷小的基本性质

这三个基本性质记牢

等价无穷小的性质

第一个是常识，第二个关键记一下

当x -> 0时，常用的等价无穷小

这里可以看一下最后一条挺有意思的，就像是e为底然后转换的那个样子，其实还挺好记的我还以为不好记

再加一个
（1+bx）^a-1 ~ abx

记牢啊，就是你随时都得有使用这些东西的意识，把式子拼凑出这个样子你就能够使用了。
用法举例：其中：看到ln就可以试着拼凑出ln(1+x)
e^x 就试着拼凑出e^x-1

两个重要极限

首先记住这两个东西

上面的东西要记住

两个重要极限

重点题型讲解

题型三 不定型极限的计算问题

这是几种题型

0/0型

这几种条件反射要形成的

这里是三阶就是可能就是对你的一个提示，对于你等价无穷小什么时候可以相减的一个提示

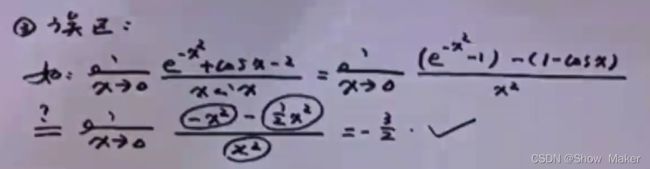
这个其实是有点扯淡的，就是你上面本来都同阶了，你可以直接减了啊喂，还在意什么呢，能减成一个项的话肯定我直接洛必达了啊，我还在意什么呢

就等价无穷小你相乘是一点问题没有，但是相加减呢就是需要看你的“精确度”就你上面的全部都是2阶的就是可以，但是你看下面的

要是一个是三阶的，一个是1阶的那就是不行。

有指数的就把指数弄下来

拆分就很有用了，还有相乘的关系，tan x和cos x 之间的关系

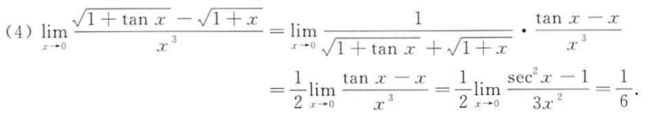
定型要和不定型区分，各放一边，然后就等价无穷小和洛必达交替使用了

1.如果有e的话你就需要考虑给它弄一个-1，然后你+1-1的话阶数不够，所以你需要提取一个出来，
2.然后多个式子之间的多种写法互换你都需要清楚
3.就你之前学到的公式，你需要把它融汇贯通地活学活用

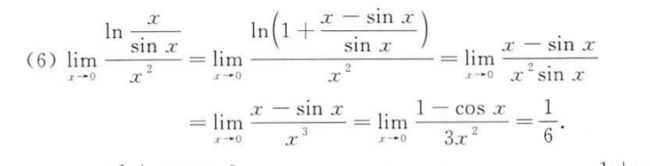
1.看到ln的条件反射
2.如果是乘除，那么直接用等价无穷小替换
3.洛必达
4.等价无穷小

1.看到次方的条件反射
2.看到e^x的条件反射
3.看到ln的条件反射
4.等价无穷小

1.等价无穷小的反向使用，为了随大流
2.约去和换元
3.洛必达法则
4.等价无穷小

1.平方差公式
2.资源分配，这个时候可以考虑就是定型的放一边，不定型的放一边的这种方式去分配你的分母x
3.遇事不决，洛必达

1 ^∞ 型

这个就是凑出那个重要极限，值为e

1.1^∞型，凑出1
2.这一步存疑，他用了啥变换？泰勒公式？
暂时用洛必达理解

这个型的两种解题技巧：转换

1.看出了是1^∞型了你就得去硬凑出那个样子
2.然后又看出是∞*0型的你就用那个方法去左
3.看出可以换元，换元的时候要记得你趋近的符号也需要换一下范围
4.看出等价无穷小
可以看出其实很多题呢，都是你看出一步发现又一个做法能够继续走下去，然后又看出东西，又继续做

1.照样看出是1^∞，然后直接变换
2.等价无穷小公式！！！记得用（1+bx）^a=abx，这个很多地方有用

1.正常看出是1^∞型的
2.正常变化，1拉出来
3.记得要把确定的极限和不确定的极限分开，因为你确定的极限可以直接算出来就相当于是一个常数了，常数分开这很合理吧
4.然后觉得走不下去了，你要记得资源分配，两个数相减是很简单资源分配成两个数相乘的，只要你加入1就行了。



这个看最高次的就可以了
这些结论可以直接用

1.发现这两个相除的结果是一个常数，所以这两个多项式的最高次幂相等，
你可以求一下下面那个式子的最高次幂，（只需要最高次幂）
2.1最高次幂相等
2.2二项式相除的结果就是最高次幂的系数相除

多项式除以多项式的题型就是这样了，就是看你的结果了，这里结果是0，就代表下面的最高次幂的系数要大于上面的。
求一下上面的最高次幂的系数就好了。

特征：x趋于无穷，多项式最高次幂系数除一下就是结果

这个没啥好说的

∞-∞型

这个分这两种情况

无分母

1.∞-∞：提取，一定要变形，不变形是做不出来的，提取一个x²变成了∞ * 0型的，然后再按∞ * 0型的方法变成相除来做
2.看到可以换元，那就换一下元喽，换元记得趋于的范围要换一下。

1.∞ - ∞型的，但是多了一个1，把1提取出来，单独算，这种拆分出来肯定是要的，就你定型的，能算的你先给他分出来算了
2.然后就正常转换了

1.∞-∞型，分子有理化
2.分子分母同时除以x
3.直接算，有利用到无穷小×有界函数还是无穷小这个知识点

有分母

1.有分母的就直接先通分
2.然后看到这种样子你就应该想到资源分配
3.1同阶的可以直接相加（这点是汤说的，等价无穷小在同阶的时候可以直接相加）
3.2然后洛必达

∞ ⁰ 型和0⁰型

这两种型就用e去转换就可以了

1.看到是0⁰型的就马上用e去替换
2.如果是×的直接用等价无穷小替换，这个地方的等价无穷小替换需要很小心，最好还是不要用，用泰勒展开，这边直接用等价无穷小的话有几率出错。然后又变成0 * ∞了，就再次转换称除的形式