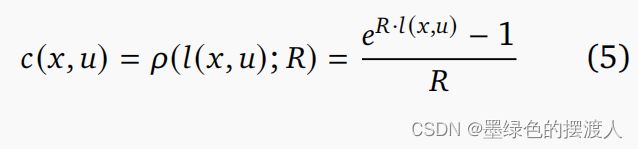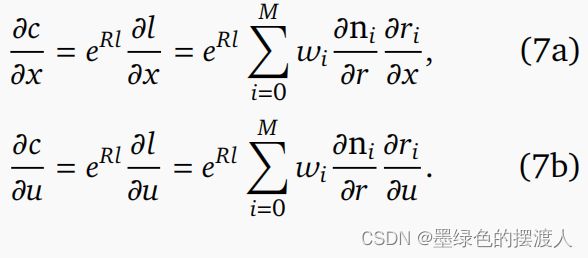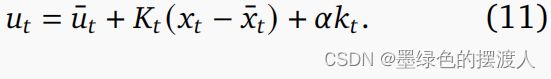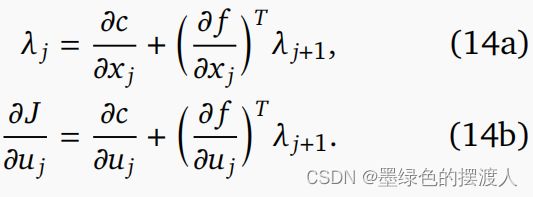论文笔记（二十三）：Predictive Sampling: Real-time Behaviour Synthesis with MuJoCo

文章概括

作者：Taylor Howell, Nimrod Gileadi, Saran Tunyasuvunakool, Kevin Zakka, Tom Erez and Yuval Tassa
来源：arXiv:2212.00541v1 [cs.RO] 1 Dec 2022
原文：https://arxiv.org/pdf/2212.00541.pdf
代码、数据和视频：
系列文章目录：
上一篇：
论文笔记（二十二）：GRiD: GPU-Accelerated Rigid Body Dynamics with Analytical Gradients
下一篇：

摘要

我们介绍了 MuJoCo MPC (MJPC)，这是一种基于 MuJoCo 物理学的实时预测控制的开源交互式应用程序和软件框架。 MJPC 允许用户轻松创作和解决复杂的机器人任务，目前支持三种基于射击的规划器：基于导数的 iLQG 和梯度下降，以及一种简单的无导数方法，我们称之为预测采样。 预测抽样被设计为基本基线，主要是因为它的教学价值，但事实证明它与更成熟的算法相比具有惊人的竞争力。 这项工作没有提出算法上的进步，而是通过直观和交互式软件优先考虑高性能算法、简单代码和基于模型的方法的可访问性。 MJPC 可在 https://github.com/deepmind/mujoco_mpc 获取，视频摘要可在 https://www.youtube.com/watch?v=Bdx7DuAMB6o 查看。

1. 介绍

基于模型的方法构成了经典控制和机器人技术的基础。 自从 Kalman 的开创性工作 [Kalman, 1960] 以来，状态及其动力学和观察模型一直发挥着核心作用。

经典方法正受到基于学习的方法的挑战，这些方法放弃了对状态和相关模型的明确描述，让内部表示从学习过程中出现 [Lillicrap et al., 2015, Schulman et al., 2017, Salimans et al. ., 2017, Smith 等人, 2022, Rudin 等人, 2022]。 学习表示提供的灵活性使这些方法强大而通用，但对大量数据和计算的要求使它们变得缓慢。 相比之下，纯基于模型的方法（如下所述）可以实时合成行为 [Tassa 等人，2014 年]。

由于这两种方法最终都会通过优化目标来产生行为，因此有理由相信它们可以有效结合。 事实上，众所周知的离散域突破，如 AlphaGo [Silver et al., 2016]，是结合了基于模型的搜索和基于学习的价值和策略近似。我们相信机器人和控制也可能发生同样的情况，并在讨论（第 5 节）中描述了我们对这种情况如何发生的想法。 然而，在社区迎接这一挑战之前，必须克服一个核心问题：基于模型的优化难以实现，通常依赖于精心设计的优化算法，而且通常难以实现。

为了解决这一缺陷，我们提出了 MJPC，这是一种基于 MuJoCo 物理学 [Todorov 等人，2012 年] 的预测控制开源交互式应用程序和软件框架，它使用户可以使用预测控制算法轻松编写和解决复杂任务 即时的。 该工具提供基于标准导数的算法的实现：iLQG（二阶规划器）和梯度下降（一阶规划器）。 此外，它还引入了预测采样，这是一种简单的零阶、基于采样的算法，效果出奇地好并且易于理解。

重要的是，交互式模拟可以异步减慢，从而在模拟时间方面加快规划器的速度。 这意味着可以在较旧、较慢的机器上生成行为，从而导致预测控制工具的民主化。

MJPC 和预测采样推进了我们的中心目标，即降低机器人研究中预测控制的进入门槛。 一个重要的次要目标是加快研究速度。 调整参数时，研究人员不需要等待数小时或数分钟，而是应该收到即时反馈——这将显着提高他们自己的认知表现 [Lu and Dosher, 2022]。 我们相信，使用研究人员编写的 GUI 进行灵活、交互式的模拟不仅是“可有可无”，而且是高级机器人研究的先决条件。

2. 背景

在本节中，我们提供有关最优控制和轨迹优化的一般背景，然后重点介绍预测控制和无导数优化。

最优控制： 最优控制意味着选择行动以最小化未来成本（等价地，最大化未来回报）。 具有状态 $x\in R^n$ 的动态系统，采用用户选择的控制（或动作）$u\in R^m$，根据离散时间动态演化，

$$x_{t+1}=f(x_t,u_t)\text{\hspace{1em}(1)}$$

系统的行为通过运行成本编码：$R^n\times R^m\to R_{+}，$

$$c(x_t,u_t),\text{\hspace{1em}(2)}$$

状态和控制的函数，其中明确的时间依赖性可以通过将时间折叠到状态中来实现。 未来成本（又名成本或价值）可以通过多种方式定义。 求和可以继续无穷大，导致平均成本或折扣成本公式，在时间差异学习中受到青睐，我们将在第 5 节中讨论。这里我们关注有限范围公式，由此给出优化目标 经过：

状态和控制的函数，其中明确的时间依赖性可以通过将时间折叠到状态中来实现。 未来成本（又名成本或价值）可以通过多种方式定义。 求和可以继续无穷大，导致平均成本或折扣成本公式，在时间差异学习中受到青睐，我们将在第 5 节中讨论。这里我们关注有限范围公式，由此给出优化目标 $J$ 经过：

$$J(x_{0:T},u_{0:T})=\sum _{t=0}^{T}c(x_t,u_t).\text{\hspace{1em}(3)}$$

轨迹优化： 解决有限范围最优控制问题 (1, 3)，即优化固定长度的轨迹，通常称为规划或轨迹优化。 这些算法 [Von Stryk and Bulirsch, 1992, Betts, 1998] 的历史可以追溯到阿波罗计划 [NASA, 1971, Smith and Yound, 1967]。 两类算法之间有一个重要的区别：

• 直接或同步方法将状态和控制都作为决策变量并强制执行动态(1) 作为约束。 这些方法（例如 Von Stryk [1993]）指定了一个大型的稀疏优化问题，通常使用通用软件 [Wächter and Biegler, 2006, Gill et al., 2005] 来解决。 它们的重要好处是可以表示非物理可实现的轨迹，例如为了限制最终状态，而无需最初知道如何到达它。

• 微分动态规划 [Jacobson 和 Mayne，1970] 等射击方法仅使用控制 $u_{0:T}$ 作为决策变量，并通过前向模拟强制执行动态。 在射击方法中，只能考虑物理上可实现的轨迹，但它们受益于减少的搜索空间和不必强制执行动力学的优化器。 后一个好处对于刚性系统尤其重要，例如那些有接触的系统，其中物理和非物理轨迹之间的差异可能非常小。 与需要动力学导数的直接方法不同，射击方法可以采用无导数优化，如下所述。

预测控制： 预测控制的关键思想发明于 60 年代末，首次发表于 [Richalet 等人，1978 年]，是在系统动态变化时实时使用轨迹优化。 此类算法已成功部署在众多现实环境中，包括：化学和核过程控制 [Na et al., 2003, Lopez-Negrete et al., 2013]，自动驾驶汽车导航 [Falcone et al., 2007] ]，以及人形机器人的全身控制 [Kuindersma et al., 2016]。

在实时设置中，需要估计或测量当前状态$x$，并且需要轨迹优化器为有限范围（这里通常称为后退范围）问题返回一组最优或接近最优的控制， 从$x$开始。 我们使用 $\Pi$ 来表示计划，即有限范围策略。 在射击方法 $\Pi =u_{0:T}$ 的上下文中，尽管正如我们稍后讨论的那样，在某些情况下它可以重新参数化，而不是直接使用离散时间控制序列。 预测控制最好从两个异步过程的角度来考虑，即代理和规划器：

预测控制具有以下显着特性：

• 更快的计算可以提高性能。 原因很明显，规划器在一个单位时间内可以采取的优化步骤越多，优化的控制序列就越好。

• 热启动具有很大的有益效果。 通过重用先前计划步骤中的计划，优化器只需进行少量修改即可纠正新状态隐含的变化。 热启动还导致跨多个规划步骤的优化过程的摊销。

• 优化不需要收敛，只需要改进，见第 5.1 节。

• 行为时间尺度比计划范围长得多的任务$T$通常仍然可以解决，尽管此属性取决于任务。

• 预测控制器很容易陷入局部极小值，尤其是那些使用导数的控制器。 这是由于优化的短视性质，可以通过使用价值函数近似值终止 rollout 来解决，请参阅第 5.3 节。

无导数优化： 我们最初关注拍摄方法的主要原因之一是它们能够利用无导数优化，也称为基于采样的优化 [Audet and Hare, 2017]。 尽管没有利用问题结构或梯度信息，这类算法可以发现复杂的行为 [Salimans et al., 2017, Mania et al., 2018]。

基于抽样的方法维护策略参数的搜索分布并评估抽样点的目标以找到改进的解决方案。 流行的算法包括：随机搜索 [Matyas, 1965]、遗传算法 [Holland, 1992] 和进化策略 [Rechenberg, 1973]，包括 CMA-ES [Hansen 和 Ostermeier, 2001]。

这类算法具有许多理想的特性。 首先，因为不需要导数信息，它们非常适合具有非平滑和不连续动态的任务。 其次，这些方法很容易并行化。

基于采样的方法已在预测控制环境中使用，但不是很广泛。 值得注意的例外是 Hämäläinen 的作品 [Hämäläinen et al., 2014, 2015]，它是 MJPC 的早期先驱，以及 Theodorou 的作品，包括 [Williams et al., 2017] 和相关论文。 虽然这些方法通常被认为样本效率低下，但我们在下面解释了为什么它们具有惊人的竞争力，特别是在预测控制的背景下。

3. MuJoCo MPC (MJPC)

我们介绍了 MJPC，这是一种用于预测控制的开源交互式应用程序和软件框架，它使用户可以使用预测控制算法实时轻松地综合复杂系统的行为。 行为由具有风险意识的简单、可组合的目标指定。 规划器，包括：梯度下降、迭代线性二次高斯 (iLQG) 和预测采样，都是用 C++ 实现的，并广泛利用多线程进行并行部署。 该框架是异步的，可以降低仿真速度并模拟更快的控制器，从而使该工具可以在慢速机器上运行。 直观的图形用户界面支持与环境的实时交互，并能够修改任务参数、计划器和模型设置，并立即查看修改的效果。 该工具位于：https://github.com/deepmind/mujoco_mpc。

3.1. 物理模拟

我们使用开源物理引擎 MuJoCo [Todorov et al., 2012] 的 API 构建 MJPC。 MuJoCo 是机器人算法交互式框架的良好基础设施，主要原因有两个：首先，MuJoCo 通过提供线程安全的 API 支持并行模拟多个候选未来轨迹，最大限度地利用现代多核 CPU 架构； 其次，MuJoCo 提供了比实时更快的高维系统模拟，具有许多接触——例如，类人动物（27-DoF 系统）在单个 CPU 线程上的模拟速度比实时快 4000 倍。

图 1 | 风险转换(;)。 对于风险参数 的不同值，该函数在 0 和 1 之间进行评估。

3.2. 目标

MJPC 提供方便的实用程序来轻松设计和组合成本以指定目标 (3)； 以及自动高效地计算导数。

费用： 我们使用以下形式的“基本成本”：

$$l(x,u)=\sum _{i=0}^M{w}_i\cdot n_i(r_i(x,u)).\text{\hspace{1em}(4)}$$

这个成本是 $M$ 项的总和，每项包括：

• 非负权重 $w\in R_{+}$ 确定该术语的相对重要性。

• 二次可微范数 $n(\cdot ):R^p\to R_{+}$，它在 $0^p$ 处取最小值。

• 残差 $r\in R^p$ 是“任务解决时很小”的元素向量。

风险敏感性： 我们通过风险感知指数标量变换 $\rho :R_{+}\times R\to R$ 来增加基本成本 (4)，对应于经典的风险敏感控制框架 [Jacobson, 1973, Whittle, 1981]。 最终运行成本 $c$ 由下式给出：

标量参数 ∈ R 表示风险敏感性。 = 0（默认值）被解释为风险中性， > 0 为风险厌恶， < 0 为风险寻求。 映射（参见图 1）具有以下属性：

• 任何的定义和平滑。
• 如果 = 0，则恒等式(; 0) = （在极限内）。
• 零是不动点：(0; ) = 0。
• 0 处的导数为 1：(0; )/ = 1。
• 非负：如果 ≥ 0 则 (; ) ≥ 0。
• 单调：(; ) > (; ) 如果 > 。
• 如果 < 0 则 是有界的：$\rho (l;R)<-\frac{1}{R}$。
• (; ) 与 的单位相同。

请注意，对于负 ，转换 产生的成本类似于强化学习中常用的有界奖励。 例如，当对某些 SPD 矩阵 $W={\Sigma }^{-1}$ 和风险参数 = −1 使用二次范数 $n(r)=r^{T}Wr$ 时，我们得到倒高斯成本 $c=1-e^{-r^T{\Sigma }^{-1}r}$， 其最小化相当于高斯的最大似然最大化。 这导致了对 RL 中常用的有界奖励作为风险寻求的有趣解释。 我们不会在本文中进一步研究这种关系。

衍生品： MuJoCo 提供了一种用于计算动力学的有限差分 (FD) 雅可比矩阵的实用程序，它在两个方面都很有效。 首先，在可能的情况下避免重新计算，例如在对控制进行差分时，不会重新计算仅取决于位置和速度的数量。其次，由于 FD 计算成本与输入的维度成比例，因此可以廉价地添加输出。 MuJoCo 的步进函数’,=(,)，计算模型中定义的下一个状态’和传感器值。 因为雅可比矩阵的 FD 近似，

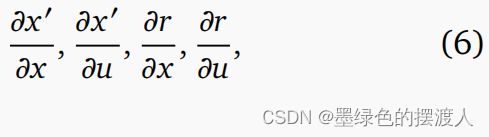
像 和 的组合维度这样的尺度，添加更多传感器 实际上是“免费的”。 MJPC 自动高效地计算成本导数如下。

梯度： 成本梯度计算如下：

范数梯度 n/ 是通过分析计算的。

Hessians： 二阶导数使用高斯-牛顿近似，忽略 $r$ 的二阶导数：

范数 Hessians ${\partial }^{2}n/\partial r^2$ 是通过分析计算的。

图 2 | 控件的时间索引样条表示。 用于构造的参数点（黑色）：零（洋红色）、线性（橙色）和三次（蓝色）插值。

3.3. 样条

正如我们在下面解释的那样，由于贝尔曼原理的要求，像 iLQG 这样的规划器需要直接控制序列表示$u_{0:T}$。 没有这个约束，控件可以被“压缩”到低维对象中。 有很多方法可以做到这一点，我们选择了最简单的：样条。 动作轨迹表示为一组时间索引的结或控制点，由一系列单调时间点 ${}_{0:P}$和参数值${\theta }_{0:P}$参数化，我们使用简写$\theta ={\theta }_{0:P}$。 给定一个查询点，样条的评估由下式给出：

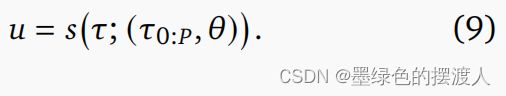
我们提供三种样条实现：传统的三次 Hermite 样条、分段线性插值和零阶保持。 有关说明，请参见（图 2）。

像样条这样的压缩表示的主要好处是它们减少了搜索空间。 它们还平滑控制轨迹，这通常是可取的。 样条函数属于线性基类，包括傅里叶基和正交多项式。 这些很有用，因为它们允许梯度从直接表示 Π 轻松传播回参数值 。 在我们的例子中，这相当于计算：

它有一个简单的解析公式（详见代码）。 与其他线性基不同，样条具有方便的属性，即限制值 也限制样条轨迹。 这对于零插值和线性插值是完全正确的，对于三次样条曲线也是如此。 边界很重要，因为大多数物理系统都将控制限制在边界内，在边界之外搜索是没有意义的。 附录 A 中提供了三次插值、线性插值和零插值的表达式。

3.4. 规划师

MJPC 包括两个基于衍生的规划器。

iLQG： iLQG^ 规划器 [Tassa 等人，2012 年]，DDP 算法的高斯-牛顿近似 [Jacobson 和 Mayne，1970 年]，利用一阶和二阶导数信息对开环控制采取近似牛顿步 序列 $u_{0:T}$ 通过动态规划 [Kalman, 1964]，产生一个时变线性反馈策略：

标称或当前最佳轨迹用上划线 (¯) 表示， 是反馈增益矩阵， 是对当前动作轨迹的改进。 执行步长 ∈ [${}_{min}$, 1] 的平行线搜索以找到最佳改进。 其他增强功能包括强制执行动作限制和自适应正则化的约束后向传递 [Tassa et al., 2014]。 iLQG 的细节过于复杂，在此不再赘述，请读者参阅上述参考资料。

梯度下降： 这个一阶规划器，被称为 Pontryagin 的最大原理 [Mangasarian，1966]，利用梯度信息来改进动作序列，这里表示为样条。 总回报的梯度用于更新样条参数，在步长∈[${}_{min}$，${}_{max}$]上使用平行线搜索：

总梯度由下式给出：

其中样条梯度Π/由（10）给出，而/Π用最大原理计算。 让表示共态，关于的梯度由下式给出：

与 iLQG 等计算成本更高的方法相比，这种一阶方法的主要优势在于，优化是在较小的样条参数空间而不是整个（非参数）动作序列上执行的。

预测抽样： 这是一种简单的、零阶的、基于采样的预测控制方法，效果很好且易于理解。 该算法被设计为基本基线，结果证明与更复杂的基于导数的算法相比具有惊人的竞争力。

算法： 用样条参数表示的标称动作序列使用随机搜索 [Matyas，1965] 进行迭代改进。 在每次迭代中，评估候选样条：标称本身和-1个来自高斯的噪声样本，标称作为其均值和固定标准差。 采样后，通过固定样条参数 将动作固定在控制限值内。 评估每个候选人的总回报，并用最佳候选人更新名义。 请参阅附录 C 中的算法 4 和伪代码。预测抽样不是创新的或高性能的，而是作为简单的基线呈现的，请参阅下面的讨论。

我们的存储库 https://github.com/deepmind/mujoco_mpc 包含一个笔记本，它使用易于理解的 Python 代码实现预测采样。

4. 结论

我们为三个示例任务提供了图形用户界面 (GUI) 的简短文本描述。 通过在 https://www.youtube.com/watch?v=Bdx7DuAMB6o&feature=youtu.be 上观看相关视频或更好地下载软件并与之交互，可以更好地理解它们。

4.1. 图形用户界面

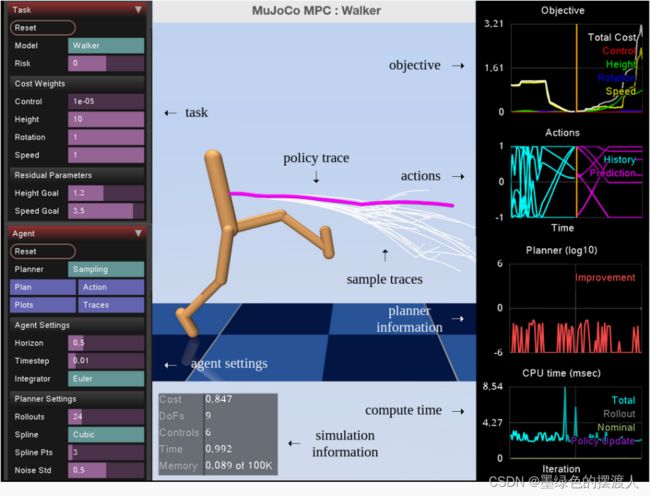
图 3 中显示和描述的 MJPC GUI 提供了一个交互式模拟环境，以及包含研究人员可以设置的实时图和参数的模块。 直观的界面使研究人员能够以交互方式更改成本参数或规划器设置并立即在模拟环境和实时图中查看结果，从而简化政策设计，从而实现快速调试并加深对影响行为的因素的理解。

图 3 | 图形用户界面。 左侧选项卡包括任务和代理模块。 在任务模块中，从下拉菜单中选择模型并设置风险值； 成本权重和残差参数使用交互式滑块指定。 代理模块提供对规划器、设置和切换规划器和控制器的开关的下拉菜单的访问。 右侧选项卡包括模拟读数和成本预测，包括个别条款和操作。 实时的、特定于规划器的信息和各种计算时间结果如下所示。 当前策略和采样轨迹的痕迹是可视化的，用户可以交互地暂停或减慢模拟并向系统施加外力和力矩。

4.2. 例子

在以下示例中，我们展示了在单个 CPU 上模拟各种高维系统的复杂运动和操纵行为的综合能力。 此外，我们证明了这些行为对干扰和模拟与规划模型之间的不匹配具有鲁棒性，并且可以在新场景中非常快速地适应。 对于所有示例，单个更新的总计划时间在 1 到 20 毫秒之间。 我们在下面重点介绍了三个示例，并提供了软件的其他示例。 附录 B 中提供了目标和规划器设置的实验细节。

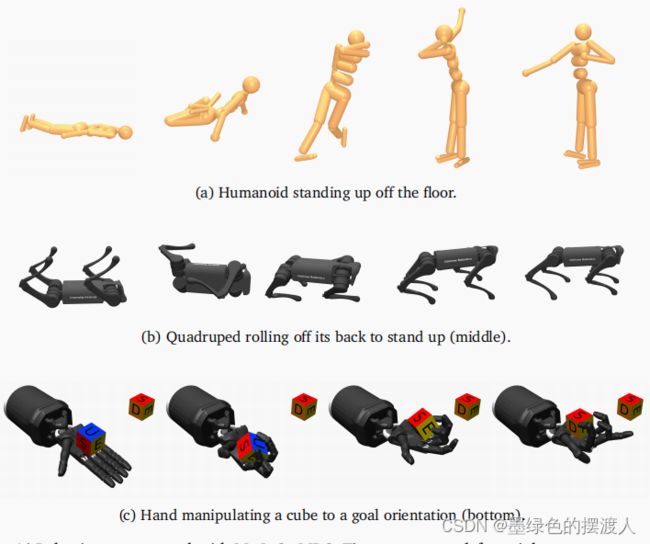
Humanoid: 这个 27-DOF 类人系统来自 DeepMind Control Suite [Tunyasuvunakool et al., 2020]，有 21 个动作，任务是站立。 该系统可以在地板上初始化，并以对大干扰具有鲁棒性的方式快速站立。 如果足够大的干扰将人形机器人撞到地板上，系统将重新站起来（图 4a）。

Quadruped: 来自 MuJoCo Menagerie [MuJoCo Menagerie Contributors, 2022] 的四足 Unitree A1 [Unitree, 2022] 表现出敏捷的行为，可以穿越不平坦的地形，包括在陡坡上行走。 在速度较慢的机器上，四足动物常常难以上升。 在这种情况下，可以有效地利用模拟减速来为计划者提供额外的模拟时间来计划成功的爬升。 该系统还能够从背上滚下来并站起来（图 4b）。 为了执行像连续导航地形这样的长距离任务，设置了一系列目标姿势。 一旦达到目标，就会发生自动转换并设置下一个目标。

Hand: 同样来自 MuJoCo Menagerie 的 Shadow Hand [Tuffield and Elias, 2003]，将立方体手动操作到所需的方向（图 4c），研究人员可以通过交互式设置目标方向来实时设置此目标。手部重新定向——具有复杂接触动力学的高自由度系统——被认为难以解决 [Chen et al., 2021]，据我们所知，以前尚未从头开始实时解决。

图 4 | 使用 MuJoCo MPC 生成的行为。 时间从左到右进行。

5. 讨论

本文的主旨是通过可定制的、交互式的、开源的工具来实现预测控制。 我们相信响应式、基于 GUI 的工具是加速机器人研究的先决条件，并且由于它们的重要性，这些工具应该是可修改的，并且内部工作对研究人员来说是透明的。 我们希望我们的 MJPC 项目能够被社区所接受，并期待共同完善和扩展它。

5.1. 预测抽样

这种简单方法的有效性表明，快速、近似优化可以与更复杂的方法竞争，后者返回更好的解决方案但速度更低。 较高的计划率是否可以完全解释这种惊人的有效性？ 我们相信还有另一个更微妙的原因。 传统优化的原则并没有很好地描述预测控制。 例如，采取不止一个优化步骤通常是没有意义的。 一旦单次迭代完成，测量状态的新值并重新规划比继续收敛到已经过时的问题的最小值更重要。 优化格局的不断变化使预测控制成为一个性质不同的问题，更像是冲浪而不是登山。 目标不是找到最小值，而是保持在最小值的吸引力盆地中。 这是一个不同的、较弱的标准，在这个标准下，简单的算法比用传统的收敛标准来衡量要好。

需要明确的是，预测抽样并不是一种新颖的算法。 相反，它是一个基线。 许多现有方法的极端情况，它可以不同地描述为“具有无限温度的 MPPI”、“具有非自适应分布的 CEM”或只是“简单的随机搜索”。 存在更好的算法，但没有一个是那么容易描述或实现的。 我们引入预测抽样不是因为它好，而是因为它不好。 这是最简单的基于采样的拍摄方法，因此为性能基准建立了一个下限。

5.2. 用例

在我们讨论限制及其可能的解决方案之前，有必要问一下现在如何使用 MJPC，如上所述？

1. 任务设计： MJPC 使添加新任务、向 GUI 公开任务参数以及快速生成所需行为变得容易。 然后可以在任何其他选择的框架中重新执行该任务。 虽然我们还没有实现与时间相关的任务，但这是可能且容易的； 我们希望 MJPC 在运动跟踪任务中表现得特别出色。

2. 数据生成： MJPC 可用于为基于学习的方法生成数据，即，它可以充当“专家策略”。 在这种情况下，通常情况下生成数据的模型和任务不必与学习者使用的模型和任务完全匹配，并且数据可能对广泛的设置有用。

3. 预测控制研究： 对于对预测控制本身感兴趣的研究人员，MJPC 提供了一个理想的平台。 MJPC 可以即时切换规划器，其异步设计通过正确计算和奖励更快的规划器来提供公平的比较。

5.3. 局限和未来的工作

只能控制MuJoCo可以模拟的东西： 这是预测控制的一般限制，实际上更强，因为人们只能控制可以比实时快得多的模拟。 例如，很难想象对非常高 DoF 系统（如流体、布料或软体）进行如此快速的模拟。 一种解决方案是结合使用传统物理建模和学习来改进模拟，例如 [Ladicky et al., 2017]。 另一种可能性是完全从观察中学习动态。 这种通常被称为基于模型的强化学习的方法显示出巨大的前景 [Heess 等人，2015 年；Nagabandi 等人，2019 年；Wu 等人，2022 年]。 我们建议在可能的情况下，在尝试使用学习的动力学模型进行预测控制时，使用传统模拟器作为后备，如 [Schrittwieser et al., 2020] 中所述，以消除建模错误的影响。

近视： Predictive Control 的核心限制是它是近视的，无法超越固定的视野。 这可以通过三种概念上直接的方式得到改善：

1. 学习策略： 通过添加学习策略，来自过去事件的信息可以通过策略泛化传播到现在 [Byravan et al., 2021]。 这种方法很有吸引力，因为它只能提高性能：在推出样本时，也会推出提案策略。 如果推出更好，它将成为新的标称。 一个习得的政策也有望导致更刻板的、周期性的行为，这在运动中很重要。

2. 值函数： 用估计剩余成本的学习价值函数终止推出是增加有效范围的明显方法。 将学习到的策略和价值函数与基于模型的搜索相结合将构成“用于控制的 AlphaGo”[Silver 等人，2016 年，Springenberg 等人，2020 年]。

3. 高级代理： 预测控制器可以用作分层控制设置中的低级模块。 在这种情况下，高级代理的动作具有设置预测控制器成本函数的语义。 预测控制器保持近视，而高级代理包含任务的长期“认知”方面。 这种情况的一个好处是高级动作的频率比低级控制（例如扭矩）所需的频率低得多。

硬件： MJPC是针对机器人研究的，这就引出了一个问题，它能用来控制硬件吗？

1. 迁移学习： 如 5.2 中所述，使用 MJPC 生成数据然后传输到真实机器人已经成为可能。

2. 估计： 控制硬件的最明显但最困难的途径是跟随经典控制的脚步，并将 MJPC 耦合到提供实时状态估计的估计器。 在估计很容易的极少数情况下，例如使用固定底座操纵器和静态物体，直接使用 MJPC 控制机器人将是一个简单的练习。 困难而有趣的案例涉及自由移动的身体和接触，如运动和操纵。 对于某些特定情况，如在平坦、均匀地形上的运动，不难获得合理的估计。 对于一般情况，我们认为按照 [Lowrey et al., 2014] 的方法进行接触感知估计是可能的，但这还有待观察。 相关地，我们认为高质量的估算器也需要与 MJPC 使用的相同类型的交互式 GUI 驱动界面。