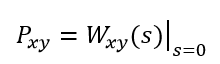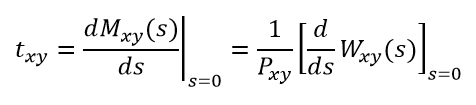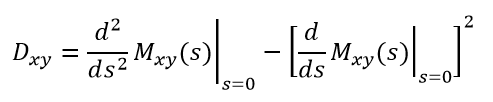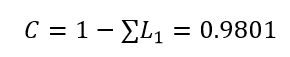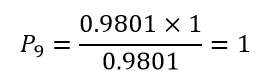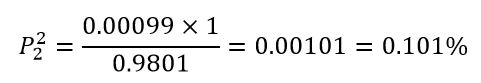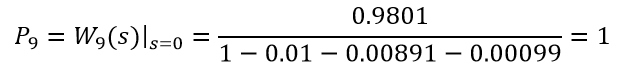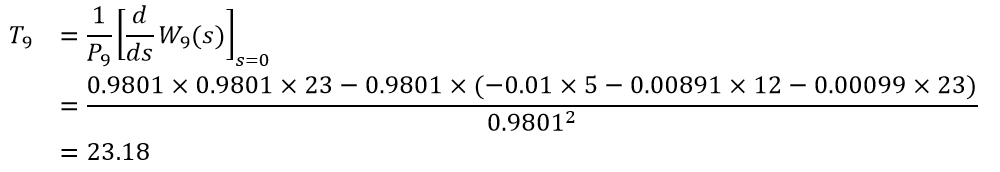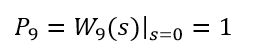网络计划经典例题讲解

请点击↑关注、收藏，本博客免费为你获取精彩知识分享！有惊喜哟！！

在实际工作中，我们能发现网络计划在经济管理中有着许多应用，本期小编选择了其中一些典型例子，包括网络计划时间参数的多种求解问题、最低成本日程问题以及随机网络（GERT）问题，进行详细讲解。

01

时间参数计算

Time parameter calculation

网络图的时间参数包括工作所需时间、事项最早、最迟时间、工作的最早、最迟时间及时差等。进行时间参数计算不仅可以得到关键路线，确定和控制整个任务在正常的进度下的最早完工期，而且在掌握非关键工作的基础上可进行人、财、物等资源的合理安排，进行网络计划的优化。

问题描述

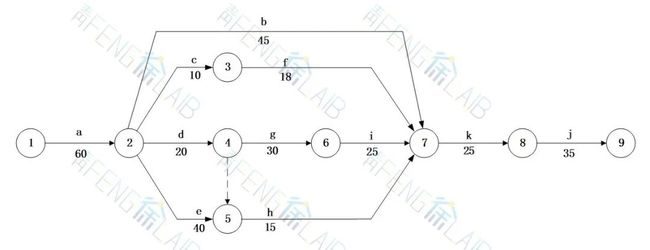
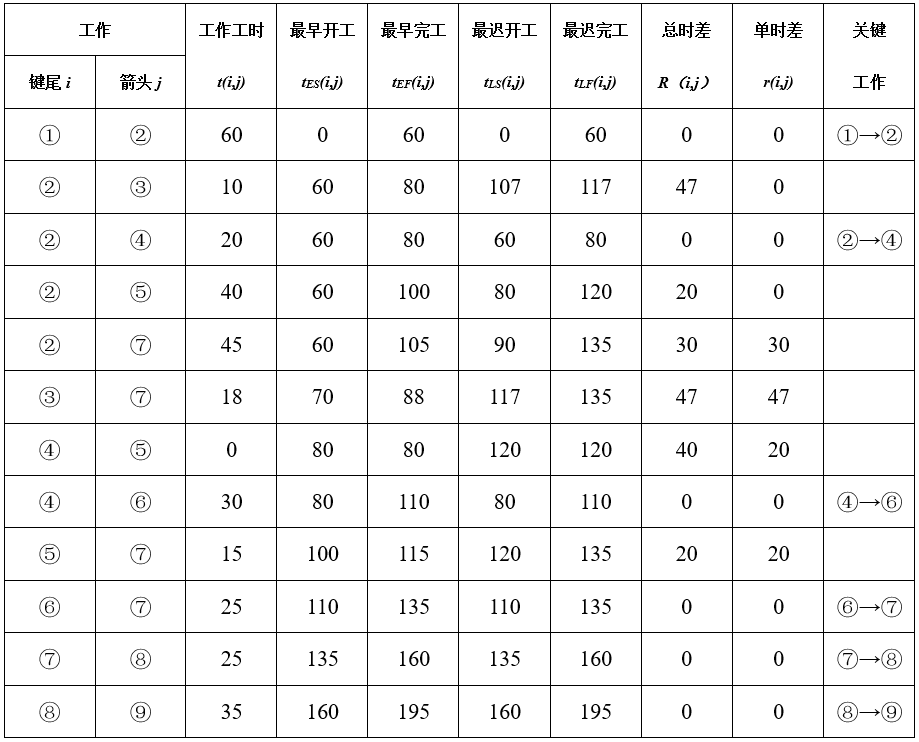
某新产品研制项目的各项工序、所需时间及相互关系如下表所示，试画出该项目的网络图，分别用和双代号、单代号方法以及表上计算法计算事项时间参数，并求出关键路线。

问题解析

1

双代号方法求解

①计算各项工作的最早开始时间和最早完成时间；

②计算各项工作的最晚开始时间和最晚完成时间；

③计算各项工作的单时差，用后一项工作的最早开始时间-本项工作的最早结束时间；

④计算各项工作的总时差。

如图所示，关键路径为总时差最小的路线，即

①→②→④→⑥→⑦→⑧→⑨

2

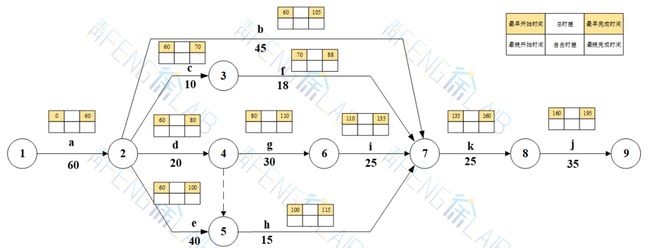
表上计算法求解

3

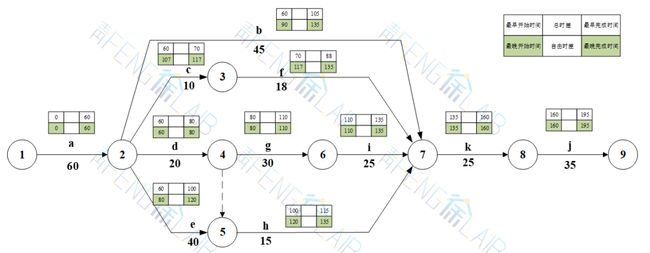
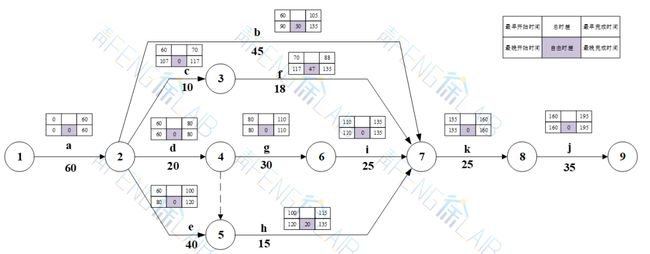
单代号方法求解

①计算各项工作的最早开始时间和最早完成时间；

②计算相邻工作之间的时间间隔；

③计算各项工作的自由时差；

④计算各项工作的总时差；

⑤计算各项工作的最晚开始时间和最晚完成时间。

4

方法总结

双代号法

双代号法通过给每个活动编号，确定其最早开始时间（ES），最晚开始时间（LS），最早完成时间（EF）和最晚完成时间（LF），进而计算出整个项目的最早完成时间（TE）和关键路径。这种方法简单易懂，适合计算量不太大的项目，但是当项目较为复杂时，计算量较大且容易出错。

单代号法

单代号法将每个活动表示成一个字母或数字，通过画出箭头来表示活动之间的关系，并在箭头上标出活动持续时间，进而计算出整个项目的最早完成时间和关键路径。这种方法比双代号法通俗易懂，计算量也较小，适合一些简单的项目，但是不够灵活，当项目变化时，需要重新绘制网络图。

表上计算法

表上计算法将每个活动表示成一个表格，通过计算每个活动的最早开始时间和最早完成时间，进而计算出整个项目的最早完成时间和关键路径。这种方法直观简便，计算量较小，灵活性较高，适用于一般的项目，但是对于较为复杂的项目，需要维护大量的计算表格，有一定的难度。 

综合来说，选择何种方法求解网络计划应考虑项目的复杂度和计算的准确性，从而选择最适合的方法。

02

最低成本日程

Lowest cost schedule

项目或任务的成本一般包括直接费用和间接费用两部分。直接费用是完成各项工作应会增加一些费用，在一定范围内，工作的作业时间越短，直接费用越大。间接费用则包括管理费、办公费等，常按任务期长短分摊，在一定条件下，工期越长，间接费用越大。工期缩短时直接费用要增加而间接费用减少，总成本是由直接费用与间接费用相加而得。通过计算网络计划的不同完工期相应的总费用，以求得成本最低的日程安排就是“最低成本日程”，又称“工期一成本”优化。

问题描述

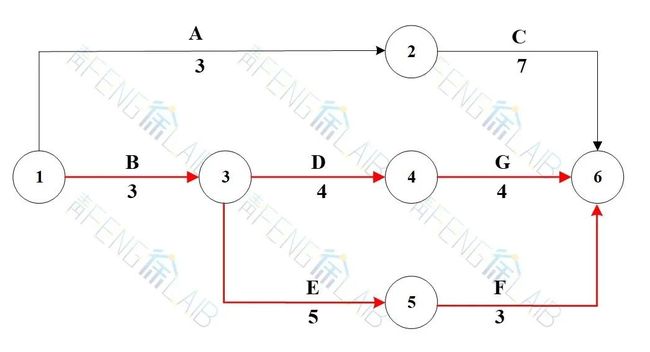
已知网络计划各工作的正常完工、极限完工及相应费用如下表所示，网络图如下图所示。

问题解析

按正常工时从下图中计算出总工期为15天。关键路线为①→③→④→⑥。由上表数据可计算出正常工时情况下总直接费用为8800元。设正常工时下，任务总间接费用为3000元，工期每缩短一天，间接费用可节省200元，求最低成本日程。

解：以上图所示的原始网络为基础，计算按下列步骤进行：

（1）从关键工作中选出缩短工时所需直接费用最少的方案，并确定该方案可能缩短的天数。

（2）按照工作的新工时，重新计算网络计划的关键路线及关键工作。

（3）计算由于缩短工时所增加的直接费用。

不断重复上述三个步骤，直到工期不能再缩短为止。

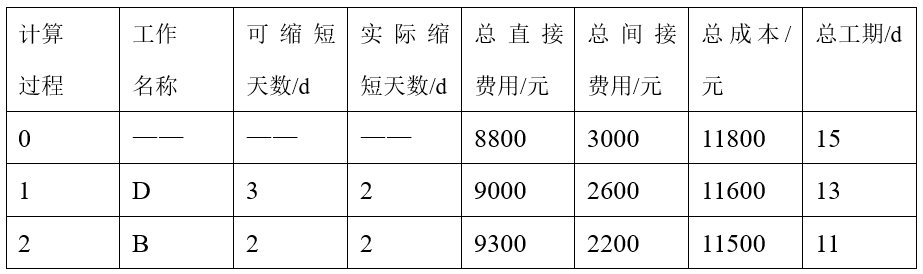
从上图看出，关键路线上的三道关键工作（1，3）、（3，4）、（4，6）中，工作（3，4）的成本斜率相比之下最小，应选择在工作（3，4）上缩短工时，查表可知，最多可缩短3天，即取工作（3，4）新工时为6-3=3（天）。重新计算网络图时间参数，结果如图a所示，关键路线为①→③→⑤→⑥，工期为13天，实际只缩短了2天。这意味着（3，4）工作没有必要减少3天，（3，4）工时应取6-2=4（天）。重新计算，结果如图b，总工期为13天，有两条关键路线：①→③→④→⑥与①→③→⑤→⑥，此次调整增加直接费用2×100=200（元）。

重复步骤（1）、（2）、（3），必须注意两条关键路线应同时缩短。有如下几个方案可选择：

①在B工作缩短1天，需要费用150（元）；

②在D、E上同时缩短1天，需费用100+120=220（元）；

③在G、E上同时缩短1天，需费用200+120=320（元）；

取费用最小方案①，最多缩短2天，工时变为5-2=3（天）。重新计算网络时间参数，结果如下图所示。总工期为11天，这时的关键路径仍为两条：①→③→④→⑥与①→③→⑤→⑥，增加直接费用2×150=300（元）。

再进行第三次调整，可供选择的方案如下：

①在D、E上同时缩短1天，需费用100+120=220（元）；

②在G、E上同时缩短1天，需费用200+120=320（元）；

因为间接费用每减少1天缩短200元，而上述方案每缩短一天增加的费用均大于间接费用，所以继续缩短工期并不能减少费用，则停止计算，计算结果如下表所示：

03

图解评审法

Illustrated review method

在之前的学习中我们知道，图解评审法GERT用随机网络来表示不确定性网络规划问题。引入完工概率和概率分支的概念，显示一项工作的完成可能有多种结果，主要用于处理超出PERT/CPM能力的更为复杂的模型情况，是经过普利茨克等人不断完善而由广义随机网络技术发展起来的网络分析法。逐步应用到存贮分析、费用分析、人口动态、车辆运输网络等不同领域。本次小编选取一道GERT网络在水利水电工程中的实际应用问题为大家进行讲解。

问题描述

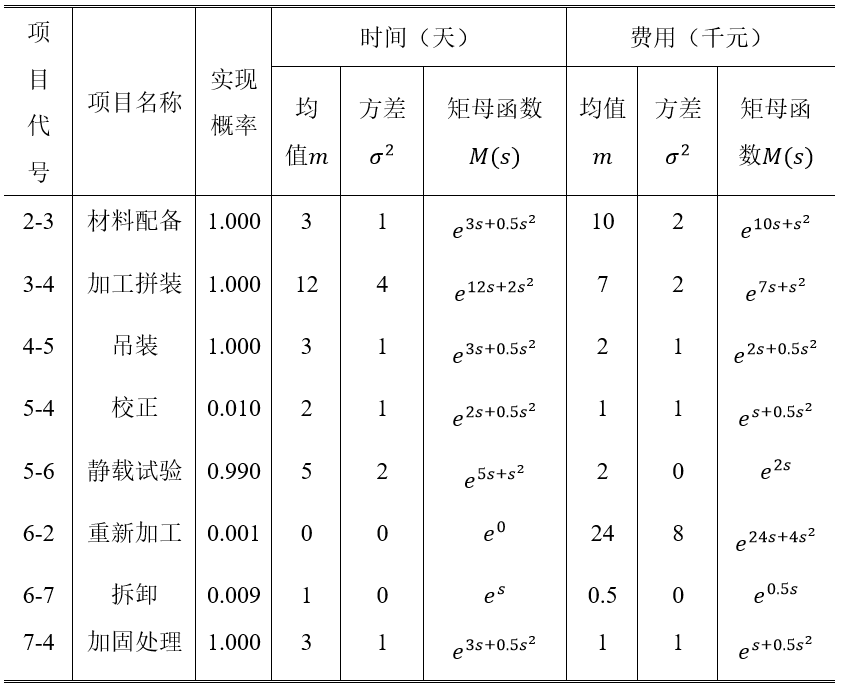
下图给出了20世纪80年代葛洲南一号船闸上游临时公路桥架设的GERT网络模型。该项工程涉及多个单位和多道工序，制作、安装、试验及运行过程中带有不少随机因素，如吊装后的符合与否，决定着静载试验能否进行，而静载试验的成功与否，又决定着能否胜利通车等。假定本模型各项目的时间和费用参数服从正态分布，于是，矩母函数式为：

式中，m为平均值，δ2为方差。有关项目的参数值如下表所示。试计算网络有关节点的实现概率Pi，节点9实现的期望时间T9和期望费用C9。

图1 一号船闸临时公路桥架设网络图

问题解析

在GERT网络模型中，网络箭线用以代表活动项目，并对项目各参数起着传递作用。GERT网络的项目参数有两类，即加因子型（如延续时间、各种资源等）参数和乘因子型（如概率等）参数。GERT网络模型的计算，对于乘因子型参数可直接采用Mason公式来确定任意一点的实现值，该公式为：

式中，B=1+(-1)n ∑线路外n阶环值Ln；C=1+(-1)n∑系统中n阶环值Ln。而对于加因子型参数，则应先将加法运算通过矩母函数转换为乘法运算，然后由Mason公式求得。该组计算式为：从节点x到y的实现概率

项目参数t在x和y节点间的数学期望值

相应的方差

问题求解

1、节点实现的概率Pi。由上图及表，可直接由Mason公式计算。先求C值：

系统中一阶回路值：

于是 ∑L1=0.0199

系统中没有二阶或二阶以上回路，故而

节点9（即完成通车）的实现概率：从节点1到9的线路仅一条，该线路上传输率之积

与该线路无非接触回路，故B=1。因此，节点9的实现概率

由上式可知，节点9肯定会被实现。这是符合情理的，因为网络无论经过多少次往复或反馈，最终通车运行是肯定的。

节点2再实现（即钢梁报废）的概率：二次到达节点2线路（仅一条）上的传输率之积

与该线无非接触回路，即B=1，于是，节点2再实现的概率为

类似地，节点7（即进行加固处理）实现的概率为

2、节点9实现的期望时间T9。采用表中的时间一栏数据，从节点1到9的线路仅一条，其时间的传输率值

该线路上无非接触回路，故∑线路上非接触回路的值=1。系统中的一阶回路值

系统中无二阶回路，于是

由此，从节点1至9时间的W函数为

由问题分析中的计算式，上述W函数在s=0处, 即为节点9的实现概率

这与前面用Mason公式直接求出的节点9的实现概率是一致的。W函数的一阶导数在s=0处的值与其概率倒数的乘积，即为节点9的期望时间，亦即整个项目的期望工期。利用分式求导法并将s=0代入，有：

因此，工程完工的期望时间为23.18天。

3、节点9实现的期望费用C9。同样的方法，采用表中费用一栏数据，可得费用的W函数为

同上，节点9的实现概率

节点9实现的期望费用，亦即整个工程的期望费用

因此，工程完工的期望费用为21.726千元。

同样道理，还可求出网络中任意一点的期望值。在此不拟逐一列出。

葛洲坝工程局以上图模型和上述计算结果指导了该项工程的实际施工，负责该桥梁架设的所有工程人员牢牢掌握带有概率型输出的节点的变化，严把质量关，尽可能避免走上回路，结果使该项目完成得既快又好，以实际工期24天和20千元的投资安全地保证了通车。