Tone Mapping中luma滤波(降噪)对噪声放大的定性分析

Tone Mapping中luma滤波对噪声放大的定性分析

在tone mapping过程中，通常经过统计之后得到一条mapping曲线，记这条曲线为$f(x)$，mapping过程中，对于给定的点，假定其亮度为$x$，映射后为$f(x)$，信号的放大增益为$k=\frac{f(x)}{x}$，上述放大增益的过程在luma平面上进行，若tone mapping在raw图像上，且像素值为$x_{raw}$,则经过tone mapping后的像素值为$k\cdot x_{raw}=x_{raw}\cdot \frac{f(x)}{x}$；为了方便讨论，我们仅讨论在luma平面进行tone mapping，那么tone mapping后的像素计算公式为$k\cdot x=x\cdot \frac{f(x)}{x}=f(x)$；

经过上面的背景介绍和铺垫，下面讨论在tone mapping过程中，对于luma平面进行降噪滤波之后再计算放大增益，对于噪声放大、边缘增强及对比度增强现象的内在原理。

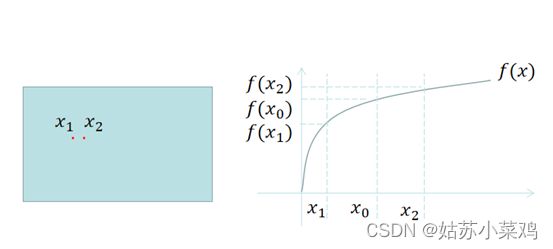
对于图像中的$x_1$，$x_2$，映射曲线为$f(x)$，那么$x_1$点映射为$f(x_1)$，$x_2$点映射为$f(x_2)$，先分析极端情况,$x_1，x_2$经过滤波的像素值均变为$x_0$，映射之后为$f(x_0)$，上述数量关系如图2所示，于是

$$k_1=\frac{f(x_1)}{x_1},k_2=\frac{f(x_2)}{x_2},k_0=\frac{f(x_0)}{x_0}$$

于是，在没有开NR时，其tone mapping后$x_1$与$x_2$的差异为：
$${\Delta }_0=k_2{x}_2-k_1{x}_1$$

开NR后，其tone mapping后$x_1$与$x_2$的差异为：
$${\Delta }_1=k_0{x}_2-k_0{x}_1$$
比较${\Delta }_0$与${\Delta }_1$的大小：
$${\Delta }_1-{\Delta }_0=\frac{f(x_0)}{x_0}(x_2-x_1)-\frac{f(x_2)-f(x_1)}{x_2-x_1}(x_2-x_1)=[\frac{f(x_0)}{x_0}-\frac{f(x_2)-f(x_1)}{x_2-x_1}](x_2-x_1)$$
由于$x_2-x_1>0$，于是只需要讨论$\frac{f(x_0)}{x_0}-\frac{f(x_2)-f(x_1)}{x_2-x_1}$的符号即可，令
$$m(x)=\frac{f(x_0)}{x_0}-\frac{f(x_2)-f(x_1)}{x_2-x_1}$$
为了分析${\Delta }_1-{\Delta }_0$的符号，我们回过头来对mapping曲线$f(x)$做一些数学层面的条件归纳：首先$f(x)$为单调函数，其一阶导数$f^{{}^{\prime }}(x)>0$，其次曲线$f(x)$的斜率在不断减小，即其一阶导数为减函数，于是$f^{{}^{\prime \prime }}(x)<0$,此外还有$f(0)=0$，于是问题简化为一个简单的数学问题：
对于$f(x)$，有$f(0)=0,f^{{}^{\prime }}(x)>0,f^{{}^{\prime \prime }}<0$，当$x\in (x_1,x_2)$时，讨论$m(x)$与0的大小

针对这个问题，我们先直观判断一下$m(x)$的符号，$\frac{f(x_2)-f(x_1)}{x_2-x_1}$为$(x_1,f(x_1))$点与$(x_2,f(x_2))$连线的斜率，$\frac{f(x_0)}{x_0}$为$(0,0)$点与$(x_0,f(x_0))$的斜率，从直观上看，后者大于前者，于是有$m(x_0)>0$，如图3所示;

下面证明这个判断，令$g(x)=\frac{f(x)}{x}$，分析其单调性，
$$g^{{}^{\prime }}(x)=\frac{x{f}^{{}^{\prime }}(x)-f(x)}{x^2}$$

要判定其单调性，只需判定其符号，而分母显然为正数，从而只需要分析分子，令
$$h(x)=x{f}^{{}^{\prime }}(x)-f(x)$$

那么
$$h^{{}^{\prime }}(x)=f^{{}^{\prime }}(x)+x{f}^{{}^{\prime \prime }}(x)-f^{{}^{\prime }}(x)=x{f}^{{}^{\prime \prime }}(x)$$
由于$x>0,f^{{}^{\prime \prime }}(x)<0$,于是$h^{{}^{\prime }}(x)<0$，从而$h(x)$为单调减函数，又有$h(0)=0-0=0$，所以$h(x)\le 0$,从而对于$x\in (0,\infty ),g^{{}^{\prime }}(x)\le 0$，从而可知，$g(x)=\frac{f(x)}{x}$为减函数。
回到$m(x)=\frac{f(x)}{x}-\frac{f(x_2)-f(x_1)}{x_2-x_1}$，对于$x\in (x_1,x_2)$其最小值为
$$m_{min}=m(x_2)=\frac{f(x_2)}{x_2}-\frac{f(x_2)-f(x_1)}{x_2-x_1}=\frac{x_{2}f(x_1)-x_{1}f(x_2)}{x_2(x_2-x_2)}$$
其分母为正数，因而只需要考虑其分子符号；对于分子$x_{2}f(x_1)-x_{1}f(x_2)$，将其除以 $x_1{x}_2$，不改变其符号，于是有
$$\frac{x_{2}f(x_1)-x_{1}f(x_2)}{x_1{x}_2}=\frac{f(x_1)}{x_1}-\frac{f(x_2)}{x_2}$$

由于前面已经分析过，$g(x)=\frac{f(x)}{x}$为减函数，以及$x_1<x_2$，有$\frac{f(x_1)}{x_1}-\frac{f(x_2)}{x_2}>0$，从而$m_{min}>0$，又由于 $x_0<x_2$，于是$m(x_0)\ge 0$，从而${\Delta }_1-{\Delta }_0>0,\frac{{\Delta }_1}{{\Delta }_0}>1$，这说明luma经过滤波之后对于相同差异的输入点，其输出差异${\Delta }_1$会比luma没经过滤波输出差异${\Delta }_0$大；反应在图像的tone mapping中，对luma降噪相对于直接tone mapping，会放大噪声，同时也增强边缘，增加对比度，也就是图1中的现象。

下面将问题放到更一般的情况，降噪将$x_1$变为$x_3$，将$x_2$变为$x_4$，大小关系为$x_1<x_3<x_4<x_2$，在曲线上的关系如图4所示

从而$k_1=\frac{f(x_1)}{x_1},k_2=\frac{f(x_2)}{x_2},k_3=\frac{f(x_3)}{x_3},k_4=\frac{f(x_4)}{x_4}$,于是有
$${\Delta }_0=\frac{f(x_2)}{x_2}{x}_2-\frac{f(x_1)}{x_1}{x}_1$$
$${\Delta }_1=\frac{f(x_4)}{x_4}{x}_2-\frac{f(x_3)}{x_3}{x}_1$$

$${\Delta }_1-{\Delta }_0=\frac{f(x_4)}{x_4}{x}_2-\frac{f(x_3)}{x_3}{x}_1-[\frac{f(x_2)}{x_2}{x}_2-\frac{f(x_1)}{x_1}{x}_1]=x_2[\frac{f(x_4)}{x_4}-\frac{f(x_2)}{x_2}]+x_1[\frac{f(x_1)}{x_1}-\frac{f(x_3)}{x_3}]$$

由于$0<x_1<x_3<x_4<x_2$以及$g(x)=\frac{f(x)}{x}$为减函数，$[\frac{f(x_4)}{x_4}-\frac{f(x_2)}{x_2}]>0,[\frac{f(x_1)}{x_1}-\frac{f(x_3)}{x_3}]>0$，从而${\Delta }_1-{\Delta }_0>0,\frac{{\Delta }_1}{{\Delta }_0}>1$；于是，对于一般情况而言，luma上降噪也会放大噪声，增强边缘，增加对比度，而且降噪强度越大，会导致luma平面越平滑，${\Delta }_1-{\Delta }_0$也变得越大，从而这种噪声放大与图像增强现象也越强。

综上，对于映射曲线满足$f(x)$为单调增函数，$f(x)$的斜率在不断减小，$f(0)=0$时，对luma平面降噪会放大图像中的噪声，增强边缘，增加对比度，而通常的tone mapping曲线$f(x)$或者整条曲线满足上述条件，或者整条曲线的一部分满足上述条件，满足上述条件的部分都会对图像进行不同程度的增强和噪声放大。