C/C++排序算法(四)—— 归并排序和计数排序
文章目录
- 前言
- 1. 归并排序
-
- 基本思想
- 算法图解
-
- 分组
- 归并
- 比较
- 动图演示
- 代码实现
- 非递归实现
-
- 情况一
- 情况二
- 情况三
- 代码实现
- 特性总结
- 2. 计数排序
-
- 基本思想
- 排序图解
- 算法升级
- 动图演示
- 代码实现
- 特性总结
- 3. 总结
前言
今天我们将学习归并排序和计数排序。
1. 归并排序
基本思想
归并排序是建立在归并操作上的一种有效的排序算法。
该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
算法图解
分组
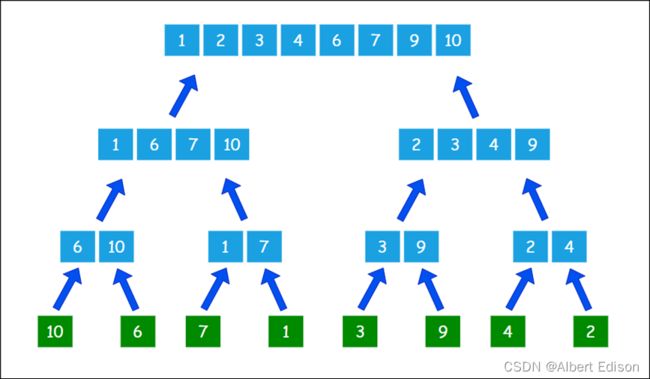
我们假设数组一共有 n 个元素,算法将会对数组进行逐层的折半分组。
第一层分成 2 个大组,每组 n/2 个元素;
第二层分成 4 个小组,每组 n/4 个元素;
第三层分成 8 个更小的组,每组 n/8 个元素;
…
一直到每组只有一个元素为止。
这样一来,整个数组就分解完成啦:
归并
既然分了组,接下来就要开始回归了。
因此,当每个小组内部比较出先后顺序以后,小组之间会展开进一步的比较和排序,合并成一个大组;大组之间继续比较和排序,再合并成更大的组…最终,所有元素合并成了一个有序的集合。
这个比较与合并的过程就叫做归并。
比较
如何把两个有序的小集合归并成一个有序的大集合呢?
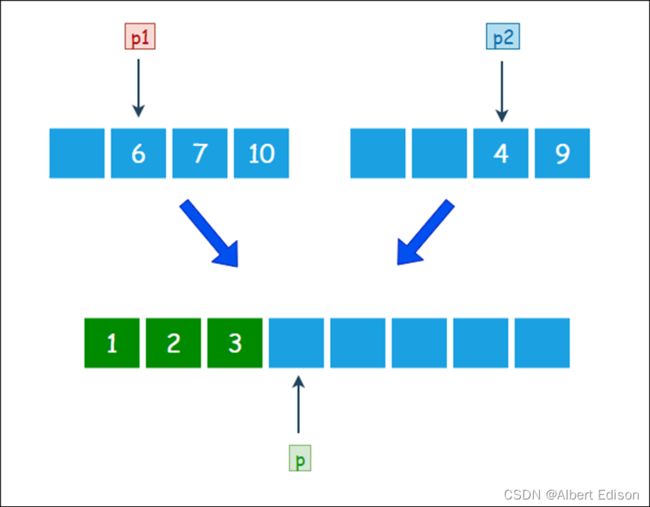
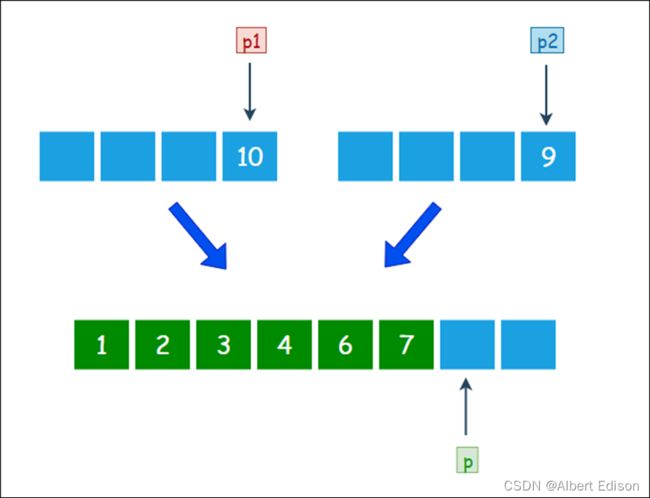
第一步,创建一个额外大集合用于存储归并结果,长度是两个小集合之和。(p1,p2,p是三个辅助指针,用于记录当前操作的位置)
第二步,从左到右逐一比较两个小集合中的元素,把较小的元素优先放入大集合。
由于 1 小于 2,所以把元素 1 放入大集合,p1 和 p 各右移一位:
由于 2 小于 6,所以把元素 2 放入大集合,p2 和 p 各右移一位:
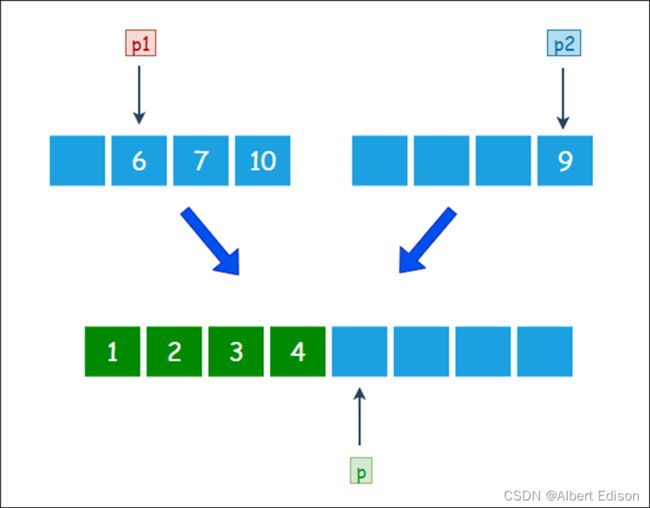
由于 3 小于 6,所以把元素 3 放入大集合,p2 和 p 各右移一位:
由于 4 小于 6,所以把元素 4 放入大集合,p2 和 p 各右移一位:
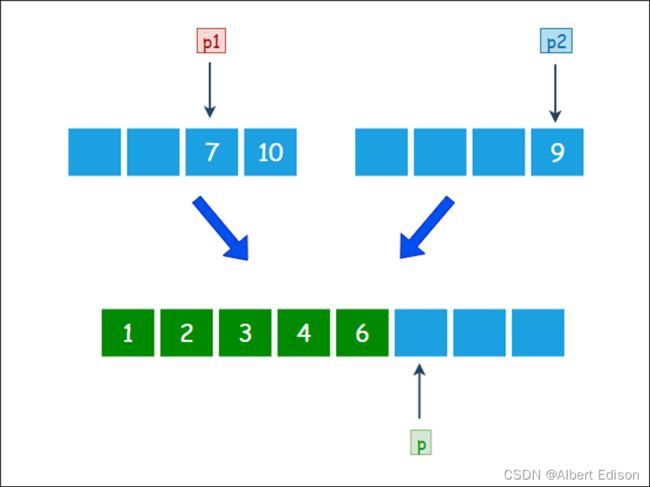
由于 6 小于 9,所以把元素 6 放入大集合,p1 和 p 各右移一位:
由于 7 小于 9,所以把元素 7 放入大集合,p1 和 p 各右移一位:
由于 9 小于 10,所以把元素 9 放入大集合,p2 和 p 各右移一位:
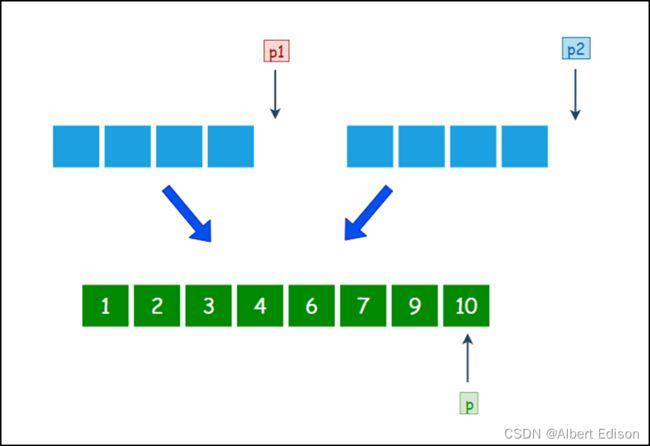
此时右侧的小集合已经没有元素可用了。
第三步,从另一个还有剩余元素的集合中,把剩余元素按顺序复制到大集合尾部。
这样一来,两个有序的小集合就归并成了一个有序的大集合。
动图演示
我们来看一下归并排序的动图吧
代码实现
代码示例
//归并排序(子函数)
void _MergeSort(int* a, int begin, int end, int* tmp) {
//如果区间不存在,直接返回
if (begin >= end) {
return;
}
// [begin, mid] [mid+1, end]
int mid = begin + ((end - begin) >> 1);
//递归让左半区间有序
_MergeSort(a, begin, mid, tmp);
//递归让右半区间有序
_MergeSort(a, mid+1, end, tmp);
//归并 左[begin, mid] 和 右[mid+1, end]
int begin1 = begin, end1 = mid;
int begin2 = mid+1, end2 = end;
int index = begin;
while (begin1 <= end1 && begin2 <= end2) {
if (a[begin1] < a[begin2]) {
//后置++,先用原来的数,再进行++
tmp[index++] = a[begin1++];
}
else {
tmp[index++] = a[begin2++];
}
}
//当遍历完其中一个区间,将另一个区间剩余的数据直接放到tmp的后面
while (begin1 <= end1) {
tmp[index++] = a[begin1++];
}
while (begin2 <= end2) {
tmp[index++] = a[begin2++];
}
//归并完后,拷贝回原数组
memcpy(a+begin, tmp+begin, (end - begin + 1) * sizeof(int));
}
//归并排序(主体函数)
void MergeSort(int* a, int n) {
//申请一个与原数组大小相同的空间
int* tmp = (int*)malloc(sizeof(int) * n); //需要一个临时的数组,去做归并的过程
if (tmp == NULL) {
exit(-1);
}
//归并排序
_MergeSort(a, 0, n - 1, tmp);
//释放空间
free(tmp);
}
int main()
{
//创建数组
int array[10] = { 9,1,2,5,7,4,8,6,3,10 };
int sz = sizeof(array) / sizeof(array[0]);
//归并排序
MergeSort(array, sz);
return 0;
}
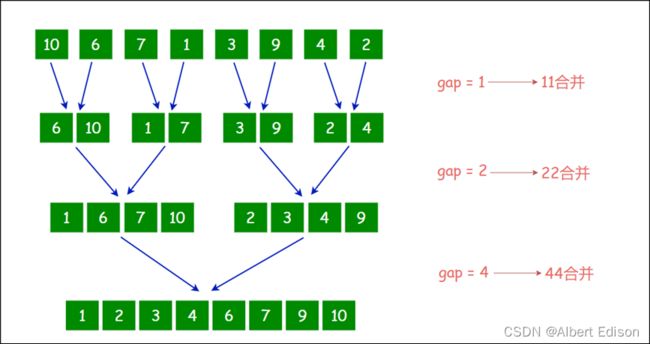
非递归实现
归并排序的非递归只需要控制每次参与合并的元素个数即可,最终便能使序列变为有序:
当然,以上例子是一个待排序列长度比较特殊的例子,我们若是想写出一个广泛适用的程序,必定需要考虑到某些极端情况。
情况一
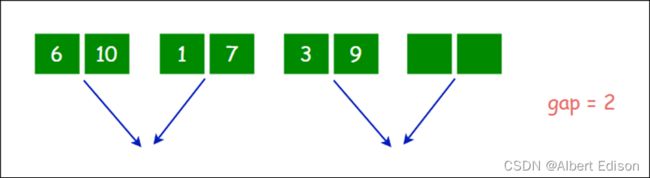
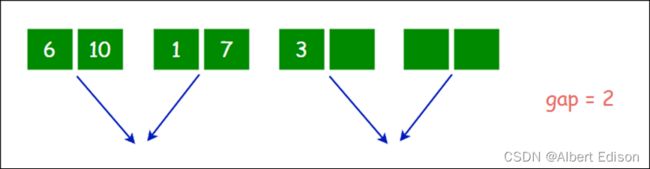
当最后一个小组进行合并时,第二个小区间存在,但是该区间元素个数不够 gap 个,这时我们需要在合并序列时,对第二个小区间的边界进行控制:
情况二
当最后一个小组进行合并时,第二个小区间不存在,此时便不需要对该小组进行合并:
情况三
当最后一个小组进行合并时,第二个小区间不存在,并且第一个小区间的元素个数不够 gap 个,此时也不需要对该小组进行合并。(可与情况二归为一类)
代码实现
非递归的实现有点复杂,需要自己画图去好好理解一下。
代码示例
//归并 --> 非递归
//先控制间距gap为1的一组开始归并
void MergeSortNonR(int* a, int n) {
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL) {
exit(-1);
}
int gap = 1;
while (gap < n) {
// 分组归并,间距为gap的是一组,两两归并
for (int i = 0; i < n; i += 2 * gap) {
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
/*
* 如果第一组越界了,那么第二组一定不存在
* 如果第一组没越界,第二组越界了,有可能不存在
*/
//如果end1越界,那么就修正到n-1的位置
//假设数组是10个元素,那么最后一个元素的下标就是9
//比如第一组是[8, 11],那么把11越界了,所以要修正到9的位置去
if (end1 >= n) {
end1 = n - 1;
}
//如果begin2>=n,说明begin2完全不存在,那么把 [begin2, end2]修正成一个不存在的区间即可
//假设数组是10个元素,那么最后一个元素的下标就是9
//比如第二组是[12, 15],那么就修正到 [10, 9]这个不存在的区间去,这样的话,下面的循环就不会进行判断
if (begin2 >= n) {
begin2 = n;
end2 = n - 1;
}
//如果begin2不越界,end2越界,修正end2即可
//假设数组是10个元素,那么最后一个元素的下标就是9
//比如第二组是[8, 15],那么把15修正到n-1的位置即可
if (begin2 < n && end2 >= n) {
end2 = n - 1;
}
int index = i;
//归并
while (begin1 <= end1 && begin2 <= end2) {
if (a[begin1] < a[begin2]) {
//后置++,先用原来的数,再进行++
tmp[index++] = a[begin1++];
}
else {
tmp[index++] = a[begin2++];
}
}
//当遍历完其中一个区间,将另一个区间剩余的数据直接放到tmp的后面
while (begin1 <= end1) {
tmp[index++] = a[begin1++];
}
while (begin2 <= end2) {
tmp[index++] = a[begin2++];
}
}
//归并完后,拷贝回原数组
memcpy(a, tmp, n * sizeof(int));
//
gap *= 2;
}
//释放空间
free(tmp);
}
//测试函数
int main()
{
//创建数组
int array[10] = { 9,1,2,5,7,4,8,6,3,10 };
int sz = sizeof(array) / sizeof(array[0]);
//归并排序-非递归实现
MergeSortNonR(array, sz);
return 0;
}
特性总结
归并排序是把集合一层一层进行折半分组,如果集合长度是 N,那么折半的层数就是 logN,每一层进行归并操作的运算量是 N:

所以归并排序的时间复杂度等于每一层的数量乘以层级数,即 O ( l o g N ) O(logN) O(logN)。
每次归并所创建的额外集合都会随着方法的结束而被释放,因此这部分空间不应该累加计算。单次归并操作开辟的最大的空间是 N,所以归并排序的空间复杂度是 O ( N ) O(N) O(N)。
(1)归并的缺点在于需要 O ( N ) O(N) O(N) 的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
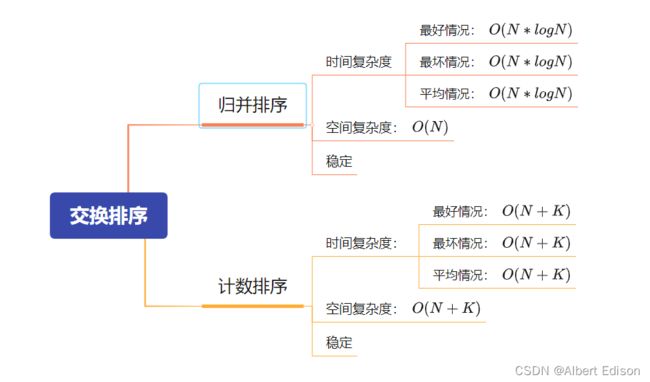
(2)时间复杂度: O ( N ∗ l o g N ) O(N*logN) O(N∗logN)
(3)空间复杂度: O ( N ) O(N) O(N)
(4)稳定性:稳定
2. 计数排序
基本思想
我们回顾一下之前所学过的排序算法,无论是冒泡排序,还是快速排序等等,都是基于元素之间的比较来进行排序。
但是有一种特殊的排序算法叫做 计数排序,这种排序算法不是基于元素比较,而是利用数组下标来确定元素的正确位置。
排序图解
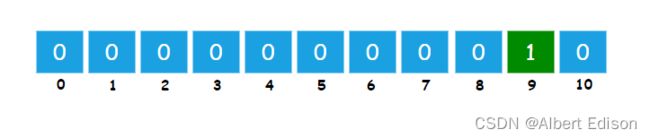
假设现在有一个数组,里面有 15 个随机整数,这些整数的取值范围是 0 到 10,那么我们先根据这个取值范围,建立一个长度为 11 的数组,数组的下标从 0 开始,数组元素全部初始化为 0。
假定 15 个随机整数的值如下:
如何给这些无序的随机整数排序呢?
很简单,让我们遍历这个无序的随机数列,每一个整数按照其值对号入座,对应数组下标的元素进行加 1 操作。
继续遍历数列并修改数组…
数组每一个下标位置的值,代表了数列中对应整数出现的次数。
有了这个 “统计结果”,排序就很简单了。直接遍历数组,输出数组元素的下标值,元素的值是几,就输出几次:

显然,这个输出的数列已经是有序的了。
这就是计数排序的基本过程,它适用于一定范围的整数排序。在取值范围不是很大的情况下,它的性能甚至快过那些 O ( l o g N ) O(logN) O(logN) 的排序。
算法升级
从大体上来说,上面的思路是没问题的,但是如果我要对下面的这组数进行排序呢:
这个数组的最大值是 99,但最小的整数是 90。如果创建长度为 100 的数组,那么按照上面的排序方法,前面从 0 到 89 的空间位置都浪费了!
怎么解决这个问题呢?
很简单,我们不再以(输入数列的最大值+1)作为统计数组的长度,而是以(数列最大值和最小值的差+1)作为统计数组的长度。
同时,数列的最小值作为一个偏移量,用于统计数组的对号入座。
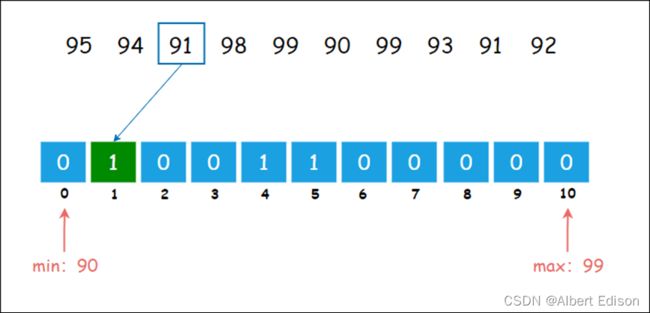
以刚才的数列为例,统计数组的长度为 99-90+1 = 10 ,偏移量等于数列的最小值 90 。

对于第一个整数 95,对应的统计数组下标是 95-90 = 5,如图所示:
对于第二个整数 94,对应的统计数组下标是 94-90 = 4,如图所示:
对于第二个整数 91,对应的统计数组下标是 91-90 = 1,如图所示:
继续遍历数列并修改数组…
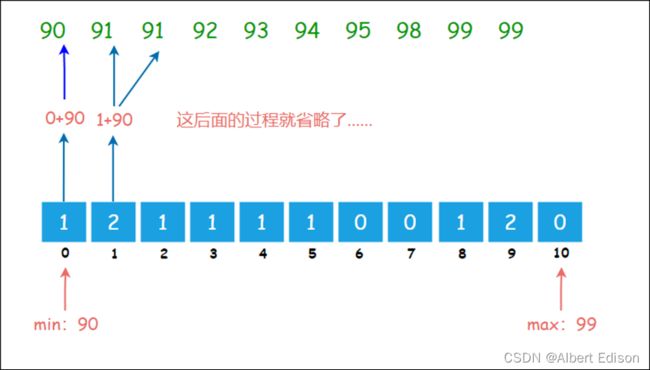
最终,数列遍历完毕时,数组的状态如下:
这时候,再次遍历数组,对应位置的值出现几次,我们就写成 下标+min,也就是 i+90:
动图演示
我们来看一下计数排序的动图过程吧
代码实现
代码示例
//计数排序
void CountSort(int* a, int n) {
int min = a[0]; //记录数组中的最小值
int max = a[0]; //记录数组中的最大值
for (int i = 1; i < n; ++i) {
if (a[i] < min) {
min = a[i];
}
if (a[i] > max) {
max = a[i];
}
}
//范围=最大值-最小值+1
//比如0-9,实际上有10个值
int range = max - min + 1; //新开辟数组的个数
int* countArray = (int*)calloc(range, sizeof(int)); //开辟可储存range个整型的内存空间,并将内存空间置0
if (countArray == NULL) {
exit(-1);
}
//统计相同元素出现次数(相对映射)
for (int i = 0; i < n; ++i) {
countArray[a[i] - min]++;
}
///根据统计结果将序列回收到原来的序列中
int j = 0;
for (int i = 0; i < range; ++i) {
//对应位置的值出现几次,就写几个
while (countArray[i]--) {
a[j++] = i + min;
}
}
//释放开辟的空间
free(countArray);
}
//测试函数
int main()
{
//创建数组
int array[10] = { 9,1,2,5,7,4,8,6,3,10 };
int sz = sizeof(array) / sizeof(array[0]);
//计数排序
CountSort(array, sz);
return 0;
}
特性总结
计数排序是一个稳定的排序算法。
当输入的元素是 n 个 0 到 k 之间的整数时,时间复杂度是 O ( n + k ) O(n+k) O(n+k),空间复杂度也是 O ( n + k ) O(n+k) O(n+k),其排序速度快于任何比较排序算法。
当 k 不是很大并且序列比较集中时,计数排序是一个很有效的排序算法。