【路径规划】局部路径规划算法——B样条曲线法(含python实现 | c++实现)
文章目录
- 参考资料
- 1. 算法简介
-
- 1.1 贝塞尔曲线的缺点
- 2. 公式原理
-
- 2.1 B样条曲线方程
- 2.2 B样条计算
- 3. B样条分类
-
- 3.1 均匀B样条曲线
- 3.2 准均匀B样条曲线
- 3.3 分段B样条曲线
- 3.4 一般非均匀B样条曲线
- 3.5 说明
- 3.6 python示例
- 3.7 c++实现
- 4. B样条曲线法实现车辆轨迹规划
参考资料
- 路径规划与轨迹跟踪系列算法
- B-spline Basis Functions
- B样条曲线(附matlab代码)
- B-样条曲线教程(B-spline Curves Notes)
- MATLAB绘制B样条曲线
1. 算法简介
- 样条是一根富有弹性的细木条或塑料条,在应用CAD/CAM技术以前,航空、船舶和汽车制造业普遍采用手工绘制自由曲线。绘制员用压铁压住样条,使其通过所有给定的型值点,再适当地调整压铁,改变样条形态,直到符合设计要求。
- 样条是通过一组指定点集而生成平滑曲线的柔性带。
- B 样条曲线就是通过控制点局部控制形状的曲线。
- B样条曲线是B-样条基函数(给定区间上的所有样条函数组成一个线性空间)的线性组合。
1.1 贝塞尔曲线的缺点
贝塞尔曲线有以下缺陷:
-
确定了多边形的顶点数(n+1个),也就决定了所定义的Bezier曲线的阶次(n次),这样很不灵活。
-
当顶点数( n+1 ) 较大时, 曲线的次数较高,曲线的导数次数也会较高,因此曲线会出现较多的峰谷值。
-
贝塞尔曲线无法进行局部修改。
B样条曲线除了保持Bezier曲线所具有的优点外,还弥补了上述所有的缺陷。即: 可以指定阶次; 移动控制点仅仅改变曲线的部分形状,而不是整体。B样条曲线是贝塞尔曲线的一般化,贝塞尔曲线可以认为是B样条曲线的特例。
2. 公式原理
2.1 B样条曲线方程
设有 P 0 , P 1 , P 2 , ⋯ , P n P_{0}, P_{1}, P_{2}, \cdots, P_{n} P0,P1,P2,⋯,Pn 一共 n + 1 \mathrm{n}+1 n+1 个控制点,这些控制点用于 定义样条曲线的走向、界限范围,则具有 n + 1 n+1 n+1个控制点的 k \mathrm{k} k 阶B样条曲线的定义为:
p ( u ) = [ P 0 P 1 ⋯ P n ] [ B 0 , k ( u ) B 1 , k ( u ) ⋮ B n , k ( u ) ] = ∑ i = 0 n P i B i , k ( u ) (1) \tag{1} p(u)=\left[\begin{array}{llll} P_{0} & P_{1} & \cdots & P_{n} \end{array}\right]\left[\begin{array}{c} B_{0, k}(u) \\ B_{1, k}(u) \\ \vdots \\ B_{n, k}(u) \end{array}\right]=\sum_{i=0}^{n} P_{i} B_{i, k}(u) p(u)=[P0P1⋯Pn]⎣⎢⎢⎢⎡B0,k(u)B1,k(u)⋮Bn,k(u)⎦⎥⎥⎥⎤=i=0∑nPiBi,k(u)(1)
式中, B i , k ( u ) B_{i, k}(u) Bi,k(u) 是第 i \mathrm{i} i 个 k k k阶B样条基函数,与控制点 P i P_{i} Pi 相对 应, k ≥ 1 k \geq 1 k≥1; u是自变量。
基函数具有如下德布尔-考克斯递推式:
B i , k ( u ) = { { 1 , u i ≤ u < u i + 1 0 , 其他 k = 1 u − u i u i + k − 1 − u i B i , k − 1 ( u ) + u i + k − u u i + k − u i + 1 B i + 1 , k − 1 ( u ) , k ≥ 2 (2) \tag{2} B_{i, k}(u)= \begin{cases} \begin{cases}1, & u_{i} \leq u
如果遇到分母为 0的情况:如果此时分子也为0,约定这一项整体为0;如果此时分子不为0,则约定分母为1 。
式中, u i u_i ui是一组被称为节点矢量的非递减序列的连续变化值,首末值一般定义为 0 和 1 ,该序列如下:
[ u 0 , u 1 , ⋯ , u k , u k + 1 , ⋯ , u n , u n + 1 , ⋯ , u n + k ] (3) \tag{3} \left[u_{0}, u_{1}, \cdots, u_{k}, u_{k+1}, \cdots, u_{n}, u_{n+1}, \cdots, u_{n+k}\right] [u0,u1,⋯,uk,uk+1,⋯,un,un+1,⋯,un+k](3)
-
K阶B样条是关于u的 k − 1 k-1 k−1次曲线(即基函数的次数为 k − 1 k-1 k−1);
-
段 数 = 控 制 点 个 数 − 次 数 = ( n + 1 ) – ( k − 1 ) = n − k + 2 段数=控制点个数-次数=(n+1) – (k-1) = n-k+2 段数=控制点个数−次数=(n+1)–(k−1)=n−k+2,(本人理解:段数的意思可以理解为一个B样条曲线含由几段贝塞尔曲线,如果有朋友有更好更恰当的解释,欢迎留言)。
-
B i , k ( u ) B_{i,k}(u) Bi,k(u)涉及到的节点为 u i , u i + 1 , . . , u i + k u_i,u_{i+1},..,u_{i+k} ui,ui+1,..,ui+k一共 k + 1 k+1 k+1个节点, k k k个区间,因此从 B 0 , k ( u ) B_{0,k}(u) B0,k(u)到 B n , k ( u ) B_{n,k}(u) Bn,k(u)共涉及 n + k + 1 n+k+1 n+k+1个节点。
-
基函数的python实现
import numpy as np ### 基函数定义 def BaseFunction(i=None, k=None, u=None, NodeVector=None): """第 i个k阶B样条基函数 Args: i (_type_, optional): _description_. Defaults to None. k (_type_, optional): B样条阶数k. Defaults to None. u (_type_, optional): 自变量. Defaults to None. NodeVector (_type_, optional): 节点向量. array([u0,u1,u2,...,u_n+k],shape=[1,n+k+1]. Returns: _type_: _description_ """ if k == 1: # 0次B样条(1阶B样条) if u >= NodeVector[0, i] and u < NodeVector[0, i + 1]: Bik_u = 1 else: Bik_u = 0 else: # 公式中的两个分母 denominator_1 = NodeVector[0, i + k - 1] - NodeVector[0, i] denominator_2 = NodeVector[0, i + k] - NodeVector[0, i + 1] # 如果遇到分母为 0的情况: # 1. 如果此时分子也为0,约定这一项整体为0; # 2. 如果此时分子不为0,则约定分母为1 。 if denominator_1 == 0: denominator_1 = 1 if denominator_2 == 0: denominator_2 = 1 # 递归 Bik_u = (u - NodeVector[0, i]) / denominator_1 * BaseFunction(i, k - 1, u, NodeVector) + \ (NodeVector[0, i + k] - u) / denominator_2 * \ BaseFunction(i + 1, k - 1, u, NodeVector) return Bik_u
2.2 B样条计算
根据公式(2)的递推式,当阶数k=1时,u在第 i i i个节点区间 [ u i , u i + 1 ) [u_i, u_{i+1}) [ui,ui+1)上基函数 B i , 1 ( u ) B_{i,1}(u) Bi,1(u)是1。不同基函数的非零域如下图:

当 k > 1 k>1 k>1时,我们使用如下三角计算格式。所有节点区间列在左边(第一)列,所有零次基函数在第二列。

如上图所示,假设需要计算 B i , 2 ( u ) B_{i,2}(u) Bi,2(u),那么就需要知道 B i , 1 ( u ) B_{i,1}(u) Bi,1(u)和 B i + 1 , 1 ( u ) B_{i+1,1}(u) Bi+1,1(u),因此我们需要先计算出 B 0 , 1 ( u ) , B 1 , 1 ( u ) , B 2 , 1 ( u ) B_{0,1}(u), B_{1,1}(u), B_{2,1}(u) B0,1(u),B1,1(u),B2,1(u)……,然后相对应地计算出 B 0 , 2 ( u ) , B 1 , 2 ( u ) , B_{0,2}(u), B_{1,2}(u), B0,2(u),B1,2(u),……。然后将所有计算出的 B i , 2 ( u ) B_{i,2}(u) Bi,2(u)放在第三列,以此类推,将 B i , 3 ( u ) B_{i,3}(u) Bi,3(u)放在第4列……。继续这个过程直到所有需要的 B i , k ( u ) B_{i,k}(u) Bi,k(u)计算完毕。
示例计算
例如,我们有4个节点 u 0 = 0 , u 1 = 1 , u 2 = 2 , u 3 = 3 u_0=0,u_1=1,u_2=2,u_3=3 u0=0,u1=1,u2=2,u3=3(为计算方便,假设都是整数值)。节点区间分别为 [ 0 , 1 ) , [ 1 , 2 ) , [ 2 , 3 ) [0,1),[1,2),[2,3) [0,1),[1,2),[2,3)。0次基函数 B 0 , 1 ( u ) B_{0,1}(u) B0,1(u)在区间 [ 0 , 1 ) [0,1) [0,1)为1,在其他区间为0; B 1 , 1 ( u ) B_{1,1}(u) B1,1(u)在区间 [ 1 , 2 ) [1,2) [1,2)为1,在其他区间为0; B 2 , 1 ( u ) B_{2,1}(u) B2,1(u)在区间 [ 2 , 3 ) [2,3) [2,3)为1,在其他区间为0。
现在计算 B 0 , 2 ( u ) B_{0,2}(u) B0,2(u),由递推式可知
B 0 , 2 ( u ) = u − u 0 u 1 − u 0 B 0 , 1 ( u ) + u 2 − u u 2 − u 1 B 1 , 1 ( u ) = u B 0 , 1 ( u ) + ( 2 − u ) B 1 , 1 ( u ) \begin{aligned} B_{0,2}(u)&=\frac{u-u_{0}}{u_{1}-u_{0}} B_{0, 1}(u)+\frac{u_{2}-u}{u_{2}-u_{1}} B_{1, 1}(u)\\ &=uB_{0, 1}(u)+(2-u)B_{1, 1}(u) \end{aligned} B0,2(u)=u1−u0u−u0B0,1(u)+u2−u1u2−uB1,1(u)=uB0,1(u)+(2−u)B1,1(u)
因为 B 0 , 1 ( u ) B_{0, 1}(u) B0,1(u)在 [ 0 , 1 ) [0,1) [0,1)上非零且 B 1 , 1 ( u ) B_{1, 1}(u) B1,1(u)在 [ 1 , 2 ) [1,2) [1,2)上非零,如果 u 在 [ 0 , 1 ) u在[0,1) u在[0,1)上 B 0 , 2 ( u ) = u B 0 , 1 ( u ) = u B_{0,2}(u)=uB_{0, 1}(u)=u B0,2(u)=uB0,1(u)=u;如果 u 在 [ 1 , 2 ) u 在[1,2) u在[1,2)上, B 0 , 2 ( u ) = ( 2 − u ) B 1 , 1 ( u ) = 2 − u B_{0,2}(u)=(2-u)B_{1, 1}(u)=2-u B0,2(u)=(2−u)B1,1(u)=2−u。
相似的计算得到 B 1 , 2 ( u ) = u − 1 B_{1,2}(u)= u - 1 B1,2(u)=u−1如果 u 在 [ 1 , 2 ) u 在[1,2) u在[1,2)上, 而 B 1 , 2 ( u ) = 3 − u B_{1,2}(u) = 3 - u B1,2(u)=3−u 如果 u 在[2,3)上。
一步一步下去,就可以计算出 B 0 , 3 ( u ) B_{0, 3}(u) B0,3(u)等。
3. B样条分类
注意:下面的分类中关于重复度的问题有些文章不太一样,只是因为定义的 k k k含义不同(本文是把 k k k定义为样条的阶数,其它文章是定义成曲线的次数,而曲线的次数=样条的阶数-1),但计算其实都是一致的。
根据节点 u u u的取值,可以划分为以下几种类型:
3.1 均匀B样条曲线
当节点沿参数轴均匀等距分布, 为均匀B样条曲线,如 U = { 0 , 1 7 , 2 7 , 3 7 , 4 7 , 5 7 , 6 7 , 1 } U=\{0,\frac{1}{7},\frac{2}{7},\frac{3}{7},\frac{4}{7},\frac{5}{7},\frac{6}{7},1\} U={0,71,72,73,74,75,76,1}。 当n和k一定时,均匀B样条的基函数呈周期性,所有基函数有相同形状,每个后续基函数仅仅是前面基函数在新位置上的重复。
定义很简单,如下:
NodeVector = np.array([np.linspace(0, 1, n + k + 1)]) # 均匀B样条节点向量,首末值定义为 0 和 1
3.2 准均匀B样条曲线
其节点矢量中两端节点具有重复度 k k k(即样条的阶数),即 u 0 = u 1 = . . . = u k − 1 , u n + 1 = u n + 2 = . . . = u n + k u_0=u_1=...=u_{k-1},u_{n+1}=u_{n+2}=...=u_{n+k} u0=u1=...=uk−1,un+1=un+2=...=un+k,所有的内节点均匀分布,具有重复度1。 如 U = { 0 , 0 , 0 , 1 , 2 , 3 , 4 , 5 , 5 , 5 } U=\{0,0,0,1,2,3,4,5,5,5\} U={0,0,0,1,2,3,4,5,5,5} 。
准均匀B样条曲线保留了贝塞尔曲线在两个端点处的性质:样条曲线在端点处的切线即为倒数两个端点的连线。 准均匀B样条曲线用途最为广泛。
-
一般来说,次数越高,则曲线的导数次数也会较高,那么将会有很多零点存在,较多的导数零点就导致原曲线存在较多的极值,使曲线出现较多的峰谷值;次数越低,样条曲线逼近控制点效果越好。
-
另一方面,三次B样条曲线能够实现二阶导数连续,故最终选择准均匀三次B样条曲线作为轨迹规划的曲线比较合适。
-
python实现
def U_quasi_uniform(n = None,k = None): """准均匀B样条的节点向量计算 首末值定义为 0 和 1 Args: n (_type_, optional): n表示控制点个数-1,控制点共n+1个. Defaults to None. k (_type_, optional): B样条阶数k, k阶B样条,k-1次曲线. Defaults to None. Returns: _type_: _description_ """ # 准均匀B样条的节点向量计算,共n+1个控制顶点,k-1次B样条,k阶 NodeVector = np.zeros((1,n + k + 1)) piecewise = n - k + 2 # B样条曲线的段数:控制点个数-次数 if piecewise == 1: # 只有一段曲线时,n = k-1 NodeVector[0,n+1:n+k+1] = 1 else: for i in range(n-k+1): # 中间段内节点均匀分布:两端共2k个节点,中间还剩(n+k+1-2k=n-k+1)个节点 NodeVector[0, k+i] = NodeVector[0, k+i-1]+1/piecewise NodeVector[0,n + 1:n + k + 1] = 1 # 末尾重复度k return NodeVector
3.3 分段B样条曲线
其节点矢量中两端节点的重复度与准均匀B样条曲线相同,为 k k k。不同的是内节点(即除去两端节点后的剩余中间节点)重复度为 k − 1 k-1 k−1。该类型有限制条件,控制顶点数减1必须等于次数的正整数倍,即 n k − 1 = 正 整 数 \frac{n}{k-1}=正整数 k−1n=正整数。
-
python实现
def U_piecewise_B_Spline(n = None,k = None): """分段B样条的节点向量计算 首末值定义为 0 和 1 # 分段Bezier曲线的节点向量计算,共n+1个控制顶点,k阶B样条,k-1次曲线 # 分段Bezier端节点重复度为k,内间节点重复度为k-1,且满足n/(k-1)为正整数 Args: n (_type_, optional): 控制点个数-1,控制点共n+1个. Defaults to None. k (_type_, optional): B样条阶数k, k阶B样条,k-1次曲线. Defaults to None. Returns: _type_: _description_ """ NodeVector = np.zeros((1,n + k + 1)) if n%(k-1)==0 and k-1 > 0: # 满足n是k-1的整数倍且k-1为正整数 NodeVector[0,n + 1:n + k + 1] = 1 # 末尾n+1到n+k的数重复 piecewise = n / (k-1) # 设定内节点的值 if piecewise > 1: # for i in range(k-1): # 内节点重复k-1次 NodeVector[0, k:n+1] = 1 / piecewise # 内节点重复度k-1 else: print('error!\n' % ()) return NodeVector
3.4 一般非均匀B样条曲线
对任意分布的节点矢量 U = [ u 0 , u 1 . . . u n + k ] U=[u_0,u_1...u_{n+k}] U=[u0,u1...un+k],只要在数学上成立都可选取。
3.5 说明
值得注意的是,许多论文中的分类是open 、clamped、closed。
-
如果节点向量没有任何特别的结构,那么产生的曲线不会与控制曲线的第一边和最后一边接触,曲线也不会分别与第一个控制点和最后一个控制点的第一边和最后一边相切。如下面图a所示。这种类型的B-样条曲线称为开(open )B-样条曲线。对于开(open)B-样条曲线, u u u的定义域是 [ u k − 1 , u n + 2 ] [u_{k-1}, u_{n+2}] [uk−1,un+2]。这个定义域的问题可以参考这篇文章
-
clamped B-样条曲线即准均匀B样条曲线,如下图b。
-
通过重复某些节点和控制点,产生的曲线会是 闭(closed)曲线。 这种情况,产生的曲线的开始和结尾连接在一起形成了一个闭环如下边图c所示。

3.6 python示例
均匀、准均匀、分段B样条的画图示例python代码如下:
if __name__=='__main__':
## 数据定义
k = 3 # k阶、k-1次B样条
flag = 3 # 1,2,3分别绘制均匀B样条曲线、准均匀B样条曲线,分段B样条
# 控制点
P = np.array([
[9.036145, 51.779661],
[21.084337, 70.084746],
[37.607573, 50.254237],
[51.893287, 69.745763],
[61.187608, 49.576271]
])
n = len(P)-1 # 控制点个数-1
## 生成B样条曲线
path = [] # 路径点数据存储
Bik_u = np.zeros((n+1, 1))
if flag == 1: # 均匀B样条很简单
NodeVector = np.array([np.linspace(0, 1, n + k + 1)]
) # 均匀B样条节点向量,首末值定义为 0 和 1
# for u in np.arange(0,1,0.001):
# u的范围为[u_{k-1},u_{n+2}],这样才是open的曲线,不然你可以使用[0,1]试试。
for u in np.arange((k-1) / (n + k+1 ), (n + 2) / (n + k+1 ), 0.001):
for i in range(n+1):
Bik_u[i, 0] = BaseFunction(i, k, u, NodeVector)
p_u = P.T @ Bik_u
path.append(p_u)
elif flag == 2:# 准均匀
NodeVector = U_quasi_uniform(n, k)
for u in np.arange(0, 1, 0.005):
for i in range(n+1):
Bik_u[i, 0] = BaseFunction(i, k, u, NodeVector)
p_u = P.T @ Bik_u
path.append(p_u)
elif flag == 3:
NodeVector = U_piecewise_B_Spline(n, k)
for u in np.arange(0, 1, 0.005):
for i in range(n+1):
Bik_u[i, 0] = BaseFunction(i, k, u, NodeVector)
p_u = P.T @ Bik_u
path.append(p_u)
path = np.array(path)
## 画图
fig = plt.figure(1)
# plt.ylim(-4, 4)
# plt.axis([-10, 100, -15, 15])
camera = Camera(fig)
for i in range(len(path)):
# plt.cla()
plt.plot(P[:, 0], P[:, 1], 'ro')
plt.plot(P[:, 0], P[:, 1], 'y')
# 设置坐标轴显示范围
# plt.axis('equal')
plt.gca().set_aspect('equal')
# 绘制路径
plt.plot(path[0:i, 0], path[0:i, 1], 'g') # 路径点
# plt.pause(0.001)
# camera.snap()
# animation = camera.animate()
# animation.save('trajectory.gif')
plt.show()
3.7 c++实现
由于在自动驾驶中算法实现一般使用C++,所以我也使用C++实现了相关功能,代码结构与python代码实现类似,这边就不再做相关代码解释了。完整代码详见我的github仓库。
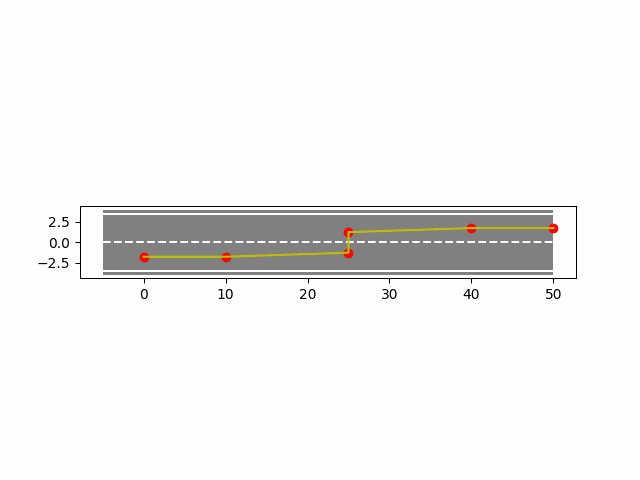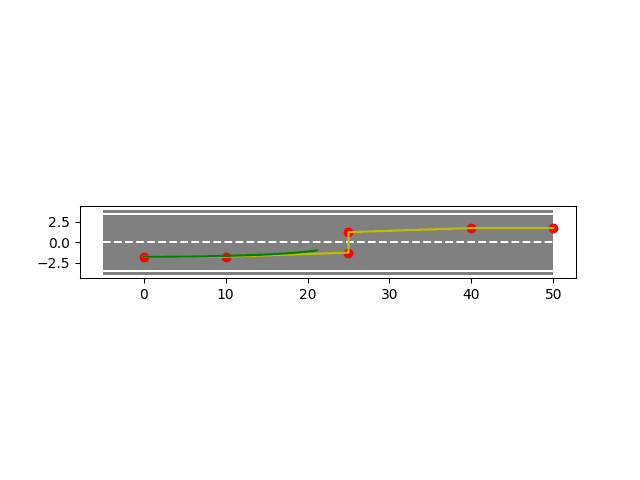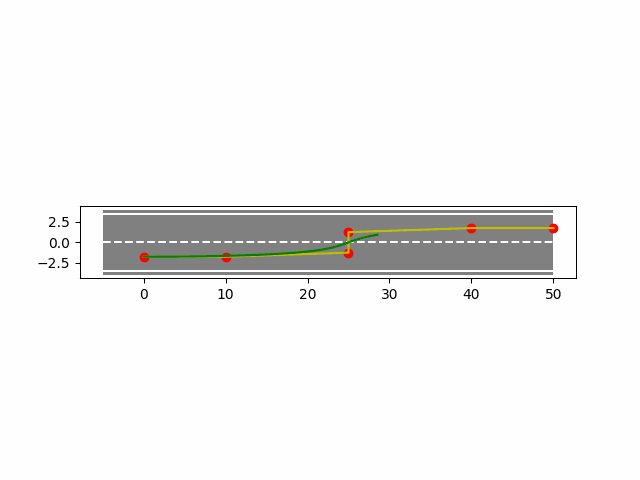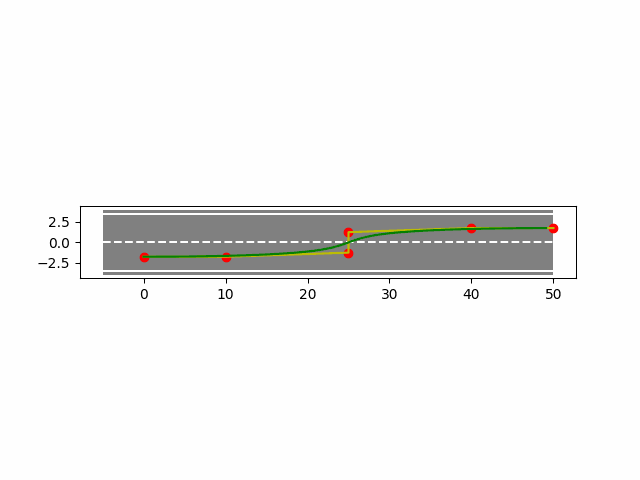
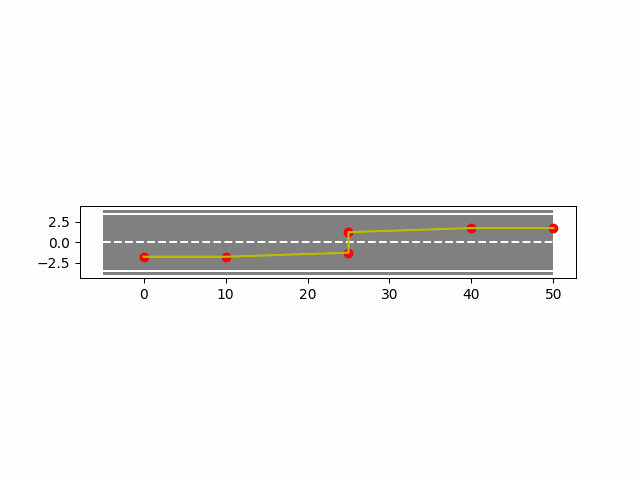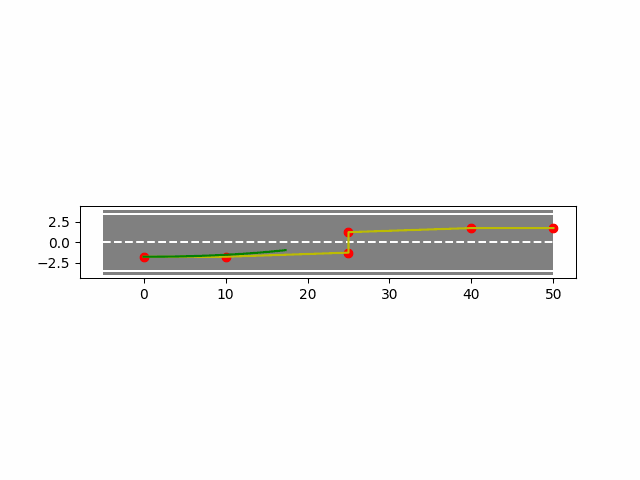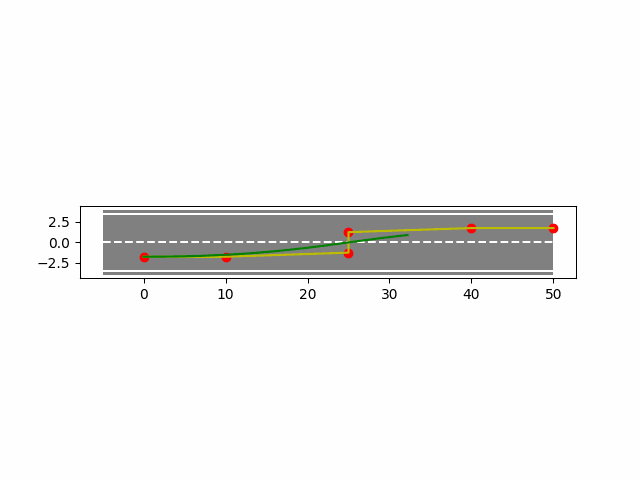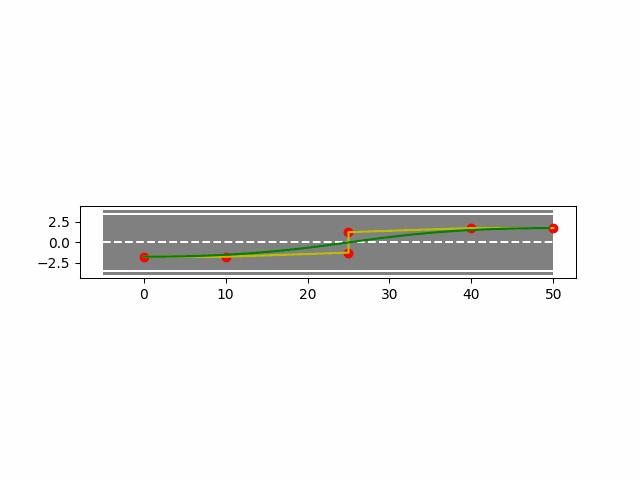
4. B样条曲线法实现车辆轨迹规划
下面使用python实现B样条曲线法在车辆上的轨迹规划。
"""B样条曲线法实现车辆轨迹规划
"""
import numpy as np
import matplotlib.pyplot as plt
import copy
from celluloid import Camera # 保存动图时用,pip install celluloid
def BaseFunction(i=None, k=None, u=None, NodeVector=None):
"""第 i个k阶B样条基函数
Args:
i (_type_, optional): _description_. Defaults to None.
k (_type_, optional): B样条阶数k. Defaults to None.
u (_type_, optional): 自变量. Defaults to None.
NodeVector (_type_, optional): 节点向量. array([u0,u1,u2,...,u_n+k],shape=[1,n+k+1].
Returns:
_type_: _description_
"""
if k == 1: # 0次B样条(1阶B样条)
if u >= NodeVector[0, i] and u < NodeVector[0, i + 1]:
Bik_u = 1
else:
Bik_u = 0
else:
# 公式中的两个分母
denominator_1 = NodeVector[0, i + k - 1] - NodeVector[0, i]
denominator_2 = NodeVector[0, i + k] - NodeVector[0, i + 1]
# 如果遇到分母为 0的情况:
# 1. 如果此时分子也为0,约定这一项整体为0;
# 2. 如果此时分子不为0,则约定分母为1 。
if denominator_1 == 0:
denominator_1 = 1
if denominator_2 == 0:
denominator_2 = 1
Bik_u = (u - NodeVector[0, i]) / denominator_1 * BaseFunction(i, k - 1, u, NodeVector) + \
(NodeVector[0, i + k] - u) / denominator_2 * \
BaseFunction(i + 1, k - 1, u, NodeVector)
return Bik_u
def U_quasi_uniform(n=None, k=None):
"""准均匀B样条的节点向量计算
首末值定义为 0 和 1
Args:
n (_type_, optional): 控制点个数-1,控制点共n+1个. Defaults to None.
k (_type_, optional): B样条阶数k, k阶B样条,k-1次曲线. Defaults to None.
Returns:
_type_: _description_
"""
# 准均匀B样条的节点向量计算,共n+1个控制顶点,k-1次B样条,k阶
NodeVector = np.zeros((1, n + k + 1))
piecewise = n - k + 2 # B样条曲线的段数:控制点个数-次数
if piecewise == 1: # 只有一段曲线时,n = k-1
NodeVector[0, n+1:n+k+1] = 1
else:
for i in range(n-k+1): # 中间段内节点均匀分布:两端共2k个节点,中间还剩(n+k+1-2k=n-k+1)个节点
NodeVector[0, k+i] = NodeVector[0, k+i-1]+1/piecewise
NodeVector[0, n + 1:n + k + 1] = 1 # 末尾重复度k
return NodeVector
def U_piecewise_B_Spline(n = None,k = None):
"""分段B样条的节点向量计算
首末值定义为 0 和 1
# 分段Bezier曲线的节点向量计算,共n+1个控制顶点,k阶B样条,k-1次曲线
# 分段Bezier端节点重复度为k,内间节点重复度为k-1,且满足n/(k-1)为正整数
Args:
n (_type_, optional): 控制点个数-1,控制点共n+1个. Defaults to None.
k (_type_, optional): B样条阶数k, k阶B样条,k-1次曲线. Defaults to None.
Returns:
_type_: _description_
"""
NodeVector = np.zeros((1,n + k + 1))
if n%(k-1)==0 and k-1 > 0: # 满足n是k-1的整数倍且k-1为正整数
NodeVector[0,n + 1:n + k + 1] = 1 # 末尾n+1到n+k的数重复
piecewise = n / (k-1) # 设定内节点的值
if piecewise > 1:
# for i in range(k-1): # 内节点重复k-1次
NodeVector[0, k:n+1] = 1 / piecewise # 内节点重复度k-1
else:
print('error!需要满足n是k-1的整数倍且k-1为正整数')
return NodeVector
if __name__=='__main__':
## 数据定义
k = 4 # k阶、k-1次B样条
flag = 2 # 1,2,3分别绘制均匀B样条曲线、准均匀B样条曲线,分段B样条
d = 3.5 # # 道路标准宽度
P = np.array([
[0, -d / 2],
[10, -d / 2],
[25, -d / 2 + 0.5],
[25, d / 2 - 0.5],
[40, d / 2],
[50, d / 2]
])
n = len(P)-1 # 控制点个数-1
## 生成B样条曲线
path = [] # 路径点数据存储
Bik_u = np.zeros((n+1, 1))
if flag == 1: # 均匀B样条很简单
NodeVector = np.array([np.linspace(0, 1, n + k + 1)]
) # 均匀B样条节点向量,首末值定义为 0 和 1
# for u in np.arange(0,1,0.001):
# u的范围为[u_{k-1},u_{n+2}],这样才是open的曲线,不然你可以使用[0,1]试试。
for u in np.arange((k-1) / (n + k + 1), (n + 2) / (n + k + 1)+0.001, 0.001):
for i in range(n+1):
Bik_u[i, 0] = BaseFunction(i, k, u, NodeVector)
p_u = P.T @ Bik_u
path.append(p_u)
elif flag == 2:
NodeVector = U_quasi_uniform(n, k)
for u in np.arange(0, 1, 0.005):
for i in range(n+1):
Bik_u[i, 0] = BaseFunction(i, k, u, NodeVector)
p_u = P.T @ Bik_u
path.append(p_u)
elif flag == 3:
NodeVector = U_piecewise_B_Spline(n, k)
for u in np.arange(0, 1, 0.005):
for i in range(n+1):
Bik_u[i, 0] = BaseFunction(i, k, u, NodeVector)
p_u = P.T @ Bik_u
path.append(p_u)
path = np.array(path)
## 画图
fig = plt.figure(1)
# plt.ylim(-4, 4)
# plt.axis([-10, 100, -15, 15])
camera = Camera(fig)
len_line = 50
# 画灰色路面图
GreyZone = np.array([[- 5, - d - 0.5], [- 5, d + 0.5],
[len_line, d + 0.5], [len_line, - d - 0.5]])
for i in range(len(path)):
# plt.cla()
plt.fill(GreyZone[:, 0], GreyZone[:, 1], 'gray')
# 画分界线
plt.plot(np.array([- 5, len_line]), np.array([0, 0]), 'w--')
plt.plot(np.array([- 5, len_line]), np.array([d, d]), 'w')
plt.plot(np.array([- 5, len_line]), np.array([- d, - d]), 'w')
plt.plot(P[:, 0], P[:, 1], 'ro')
plt.plot(P[:, 0], P[:, 1], 'y')
# 设置坐标轴显示范围
# plt.axis('equal')
plt.gca().set_aspect('equal')
# 绘制路径
plt.plot(path[0:i, 0], path[0:i, 1], 'g') # 路径点
plt.pause(0.001)
# camera.snap()
# animation = camera.animate()
# animation.save('trajectory.gif')
- 均匀B样条结果如下:
以上所有代码见github代码仓库