哈希表的是模拟实现及封装(unordered_map 和unordered_set)
1. unordered系列关联式容器
在 C++98 中, STL 提供了底层为红黑树结构的一系列关联式容器,在查询时效率可达到 ,即最差情况下 需要比较红黑树的高度次,当树中的节点非常多时,查询效率也不理想。最好的查询是log2N,进行很少的比较次 数就能够将元素找到,因此在C++11中, STL 又提供了 4 个 unordered 系列的关联式容器,这四个容器与红黑 树结构的关联式容器使用方式基本类似,只是其底层结构不同,本文中只对unordered_map 和 unordered_set进行介绍
1.1 unordered_map
1.1.1 unordered_map 的文档介绍
unordered_map 在线文档说明http://www.cplusplus.com/reference/unordered_map/unordered_map/?kw=unordered_map
1. unordered_map 是存储
2. 在 unordered_map 中,键值通常用于惟一地标识元素,而映射值是一个对象,其内容与此键关联。键 和映射值的类型可能不同。
3. 在内部 ,unordered_map 没有对
对应的 value , unordered_map 将相同哈希值的键值对放在相同的桶中。
4. unordered_map 容器通过 key 访问单个元素要比 map 快,但它通常在遍历元素子集的范围迭代方面效率较低。
5. unordered_maps 实现了直接访问操作符 (operator[]) ,它允许使用 key 作为参数直接访问 value 。
6. 它的迭代器至少是前向迭代器。
1.1.2 unordered_map 的接口说明
1. unordered_map 的构造
| 函数声明 | 功能介绍 |
|
unordered_map
|
构造不同格式的 unordered_map 对象
|
2. unordered_map 的容量
| 函数声明 | 功能介绍 |
|
bool empty() const
|
检测 unordered_map 是否为空
|
|
size_t size() const
|
获取 unordered_map 的有效元素个数
|
3. unordered_map 的迭代器
| 函数声明 | 功能介绍 |
| begin |
返回 unordered_map 第一个元素的迭代器
|
| end |
返回 unordered_map 最后一个元素下一个位置的迭代器
|
| cbegin |
返回 unordered_map 第一个元素的 const 迭代器
|
| cend |
返回 unordered_map 最后一个元素下一个位置的 const 迭代器
|
4. unordered_map 的元素访问
| 函数声明 |
功能介绍
|
| operator[] |
返回与 key 对应的 value ,没有一个默认值
|
注意:该函数中实际调用哈希桶的插入操作,用参数key与V()构造一个默认值往底层哈希桶中插入,如 果key不在哈希桶中,插入成功,返回V(),插入失败,说明key已经在哈希桶中,将key对应的value返回
5. unordered_map 的查询
| 函数声明 | 功能介绍 |
|
iterator fifind(const K& key)
|
返回 key在哈希桶中的位置
|
|
size_t count(const K& key)
|
返回哈希桶中关键码为 key 的键值对的个数
|
注意: unordered_map 中 key 是不能重复的,因此 count 函数的返回值最大为 1
6. unordered_map 的修改操作
| 函数声明 | 功能介绍 |
| insert |
向容器中插入键值对
|
| erase |
删除容器中的键值对
|
| clear() |
清空容器中有效元素个数
|
| swap |
交换两个容器中的元素
|
7. unordered_map 的桶操作
| 函数声明 | 功能介绍 |
|
size_t bucket_count()const
|
返回哈希桶中桶的总个数
|
|
size_t bucket_size(size_t n)const
|
返回 n 号桶中有效元素的总个数
|
|
size_t bucket(const K& key)
|
返回元素 key 所在的桶号
|
1.2 unordered_set
参见 unordered_set在线文档说明
1.3 在线OJ
重复n次的元素
class Solution {
public:
int repeatedNTimes(vector& nums) {
int ret = 0;
unordered_map mp;
for(const auto & e: nums)
{
mp[e]++; //统计次数
}
for(const auto &e : mp)
{
if(e.second == nums.size() / 2)
{
ret = e.first;
break;
}
}
return ret;
}
};
两个数组的交集I
class Solution {
public:
vector intersection(vector& nums1, vector& nums2) {
vector ret;
unordered_set s1,s2; //用于去重
for(const auto &e :nums1)
{
s1.insert(e);
}
for(const auto &e :nums2)
{
s2.insert(e);
}
unordered_map mp; //统计次数
for(const auto e: s1)
{
mp[e]++;
}
for(const auto e: s2)
{
mp[e]++;
if(mp[e] == 2)
ret.push_back(e);
}
return ret;
}
};
两句话中不常见的单词
class Solution {
public:
vector uncommonFromSentences(string s1, string s2) {
vector ret;
s1 +=' '; //加空格好处理
s2 +=' '; //加空格好处理
unordered_map mp;
string tmp;
for(size_t i =0; i< s1.size();++i)
{
if(s1[i] != ' ')
{
tmp += s1[i];
}
else
{
mp[tmp]++;
tmp.clear();
}
}
for(size_t i =0; i< s2.size();++i)
{
if(s2[i] != ' ')
{
tmp += s2[i];
}
else
{
mp[tmp]++;
tmp.clear();
}
}
for(const auto &e : mp)
{
if(e.second == 1)
ret.push_back(e.first);
}
return ret;
}
}; 2. 底层结构
unordered 系列的关联式容器之所以效率比较高,是因为其底层使用了哈希结构。
2.1 哈希概念
顺序结构以及平衡树 中,元素关键码与其存储位置之间没有对应的关系,因此在 查找一个元素时,必须要经 过关键码的多次比较 。 顺序查找时间复杂度为 O(N) ,平衡树中为树的高度, O(log2N ) ,搜索的效率取决 于搜索过程中元素的比较次数。
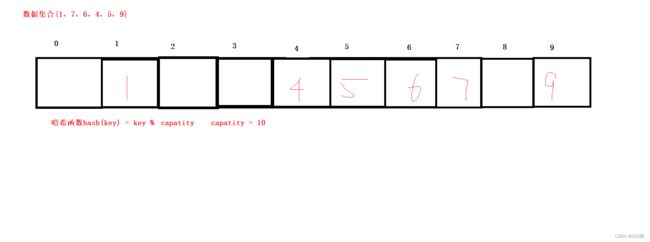
理想的搜索方法:可以 不经过任何比较,一次直接从表中得到要搜索的元素 。 如果构造一种存储结构,通过 某种函数 (hashFunc) 使元素的存储位置与它的关键码之间能够建立一一映射的关系,那么在查找时通过该函 数可以很快找到该元素 。
当向该结构中:
插入元素
根据待插入元素的关键码,以此函数计算出该元素的存储位置并按此位置进行存放
搜索元素
对元素的关键码进行同样的计算,把求得的函数值当做元素的存储位置,在结构中按此位置取元素比 较,若关键码相等,则搜索成功
该方式即为哈希( 散列 ) 方法, 哈希方法中使用的转换函数称为哈希 ( 散列 ) 函数,构造出来的结构称为哈希表 (Hash Table)( 或者称散列表 )
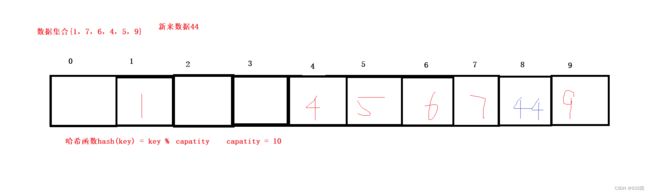
用该方法进行搜索不必进行多次关键码的比较,因此搜索的速度比较快 问题:按照上述哈希方式,向集合中插入元素44 ,会出现什么问题? 会产生哈希冲突
2.2 哈希冲突
对于两个数据元素的关键字 和 (i != j),有 != ,但有:Hash( ) == Hash( ),即:不同关键字通过相同哈希哈数计算出相同的哈希地址,该种现象称为哈希冲突或哈希碰撞。 把具有不同关键码而具有相同哈希地址的数据元素称为“同义词”。 发生哈希冲突该如何处理呢?
2.3 哈希函数
引起哈希冲突的一个原因可能是:哈希函数设计不够合理。 哈希函数设计原则:
哈希函数的定义域必须包括需要存储的全部关键码,而如果散列表允许有m个地址时,其值域必须在0 到m-1之间
哈希函数计算出来的地址能均匀分布在整个空间中
哈希函数应该比较简单
常见哈希函数
1. 直接定制法
取关键字的某个线性函数为散列地址: Hash ( Key ) = A*Key + B 优点:简单、均匀 缺点:需要事先 知道关键字的分布情况 使用场景:适合查找比较小且连续的情况
面试题: 字符串中第一个只出现一次字符
2. 除留余数法
设散列表中允许的 地址数为 m ,取一个不大于 m ,但最接近或者等于 m 的质数 p 作为除数,按照哈希函 数: Hash(key) = key% p(p<=m), 将关键码转换成哈希地址
3. 平方取中法
假设关键字为 1234 ,对它平方就是 1522756 ,抽取中间的 3 位 227 作为哈希地址; 再比如关键字为
4321 ,对它平方就是 18671041 ,抽取中间的 3 位 671( 或 710) 作为哈希地址 平方取中法比较适合:不知 道关键字的分布,而位数又不是很大的情况
4. 折叠法
折叠法是将关键字从左到右分割成位数相等的几部分 ( 最后一部分位数可以短些 ) ,然后将这几部分叠加 求和,并按散列表表长,取后几位作为散列地址。
折叠法适合事先不需要知道关键字的分布,适合关键字位数比较多的情况
5. 随机数法 -
选择一个随机函数,取关键字的随机函数值为它的哈希地址,即 H(key) = random(key), 其中 random 为 随机数函数。
通常应用于关键字长度不等时采用此法
6. 数学分析法
设有 n 个 d 位数,每一位可能有 r 种不同的符号,这 r 种不同的符号在各位上出现的频率不一定相同,可能 在某些位上分布比较均匀,每种符号出现的机会均等,在某些位上分布不均匀只有某几种符号经常出 现。可根据散列表的大小,选择其中各种符号分布均匀的若干位作为散列地址。例如:
假设要存储某家公司员工登记表,如果用手机号作为关键字,那么极有可能前7 位都是 相同的,那么我 们可以选择后面的四位作为散列地址,如果这样的抽取工作还容易出现 冲突,还可以对抽取出来的数字 进行反转( 如 1234 改成 4321) 、右环位移 ( 如 1234 改成 4123) 、左环移位、前两数与后两数叠加 ( 如 1234 改 成12+34=46) 等方法。
数字分析法通常适合处理关键字位数比较大的情况,如果事先知道关键字的分布且关键字的若干位分布 较均匀的情况
注意:哈希函数设计的越精妙,产生哈希冲突的可能性就越低,但是无法避免哈希冲突
2.4 哈希冲突解决
解决哈希冲突两种常见的方法是:闭散列和开散列
2.4.1 闭散列
闭散列:也叫开放定址法,当发生哈希冲突时,如果哈希表未被装满,说明在哈希表中必然还有空位置,那 么可以把 key 存放到冲突位置中的 “ 下一个 ” 空位置中去。 那如何寻找下一个空位置呢?
1. 线性探测
比如第一张图 中的场景,现在需要插入元素 44 ,先通过哈希函数计算哈希地址, hashAddr 为 4 ,因此 44 理论 上应该插在该位置,但是该位置已经放了值为4 的元素,即发生哈希冲突。
线性探测:从发生冲突的位置开始,依次向后探测,直到寻找到下一个空位置为止 。
插入
通过哈希函数获取待插入元素在哈希表中的位置
如果该位置中没有元素则直接插入新元素,如果该位置中有元素发生哈希冲突,使用线性探
测找到下一个空位置,插入新元素
删除
采用闭散列处理哈希冲突时,不能随便物理删除哈希表中已有的元素,若直接删除元素会影响其他 元素的搜索。比如删除元素4,如果直接删除掉,44查找起来可能会受影响。因此线性探测采用标 记的伪删除法来删除一个元素。
// 哈希表每个空间给个标记
// EMPTY此位置空, EXIST此位置已经有元素, DELETE元素已经删除
enum State{EMPTY, EXIST, DELETE};#pragma once
#include
#include
//根据STL源码库提供的扩容方案
static const unsigned long __stl_prime_list[28] =
{
53, 97, 193, 389, 769,
1543, 3079, 6151, 12289, 24593,
49157, 98317, 196613, 393241, 786433,
1572869, 3145739, 6291469, 12582917, 25165843,
50331653, 100663319, 201326611, 402653189, 805306457,
1610612741, 3221225473, 4294967291
};
static size_t GetNextPrime(size_t num)
{
for (size_t i = 0; i < 28; ++i)
{
if (__stl_prime_list[i] > num)
return __stl_prime_list[i];
}
return __stl_prime_list[27];
}
template
class Hash //如果是整型直接用自身做key
{
public:
size_t operator()(const K& key)
{
return key;
}
};
template<> //提供特化版本
class Hash
{
public:
size_t operator()(const std::string& key)
{
size_t value = 0;
for (const auto& e : key)
{
value *= 31; //通过数学推理得到的,可以31,131等。
value += e;
}
return value;
}
};
namespace CloseHash
{
enum Status //同来控制在位置的状态
{
EXIST,
EMPTY,
DELETE
};
template
class HashData //每个位置插入的数据
{
public:
std::pair _kv;
Status _status = EMPTY;
};
template>
class HashTable
{
public:
HashData* find(const K& key)
{
if (_tables.size() == 0)
return nullptr;
HashFunc hf;
size_t start = hf(key) % _tables.size();
size_t i = 0;
size_t index = start;
while (_tables[index]._status != EMPTY)
{
if (_tables[index]._kv.first == key && _tables[index]._status == EXIST)
{
return &_tables[index];
}
++i;
index = start + i;
index %= _tables.size();
}
return nullptr;
}
bool insert(const std::pair& kv)
{
HashData* ret = find(kv.first);
if (ret != nullptr)
return false;
if (_tables.size() == 0 || _n * 10 / _tables.size() >= 7) //扩容,这里可以不同,java库中是0.75
{
//size_t newSize = _tables.size() == 0 ? 10 : _tables.size() * 2;
size_t newSize = _tables.size() == 0 ? 53 : GetNextPrime(_tables.size());
HashTable newHT;
newHT._tables.resize(newSize);
for (size_t i = 0; i < _tables.size(); ++i)
{
newHT.insert(_tables[i]._kv);
}
_tables.swap(newHT._tables);
}
HashFunc hf;
size_t start = hf(kv.first) % _tables.size();
size_t i = 0;
size_t index = start;
//线性探测 or 二次探测
while (_tables[index]._status == EXIST)
{
++i;
index = start + i;
//index = start + i * i;
index %= _tables.size();
}
_tables[index]._kv = kv;
_tables[index]._status = EXIST;
++_n;
return true;
}
bool erase(const K& key)
{
HashData* ret = find(key);
if (ret == nullptr)
return false;
ret->_status = DELETE;
--_n;
return true;
}
private:
std::vector> _tables;
size_t _n = 0; //有效数据个数
};
void CloseHashTest()
{
/*HashTable ht;
int array[] = { 2,12,22,32,42,52,62,72,82 };
for (const auto &e : array)
{
ht.insert(std::make_pair(e, e));
}
ht.erase(22);
ht.erase(32);
ht.erase(42);
ht.erase(52);*/
HashTable ht;
ht.insert(std::make_pair("sort", "排序"));
ht.insert(std::make_pair("map", "地图"));
ht.insert(std::make_pair("left", "左边"));
ht.insert(std::make_pair("right", "右边"));
ht.insert(std::make_pair("apples", "苹果"));
}
}
载荷因子越大,空间占用率小,哈希冲突概率大。
载荷因子越小,空间占用率大,哈希冲突概率小。
线性探测优点:实现非常简单。
线性探测缺点: 一旦发生哈希冲突,所有的冲突连在一起,容易产生数据 “ 堆积 ” ,即:不同关键码占据 了可利用的空位置,使得寻找某关键码的位置需要许多次比较,导致搜索效率降低 。如何缓解呢?
2. 二次探测
线性探测的缺陷是产生冲突的数据堆积在一块,这与其找下一个空位置有关系,因为找空位置的方式就
是挨着往后逐个去找,因此二次探测为了避免该问题, 找下一个空位置的方法为: Hi= (H0 +i^2 )% m, 或者:Hi = (H0 -i^2 )% m 。其中: i = 1,2,3… , 是通过散列函数 Hash(x) 对元素的关键码 key 进行 计算得到的位置, m 是表的大小。 对于 2.1 中如果要插入 44 ,产生冲突,使用解决后的情况为
研究表明: 当表的长度为质数且表装载因子 a 不超过 0.5 时,新的表项一定能够插入,而且任何一个位置 都不会被探查两次。因此只要表中有一半的空位置,就不会存在表满的问题。在搜索时可以不考虑表装 满的情况,但在插入时必须确保表的装载因子 a 不超过 0.5 , 如果超出必须考虑增容。
因此:比散列最大的缺陷就是空间利用率比较低,这也是哈希的缺陷.
2.4.2 开散列
1. 开散列概念
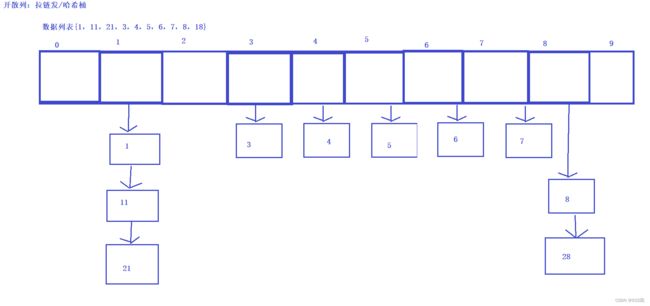
开散列法又叫链地址法(开链法),首先对关键码集合用散列函数计算散列地址,具有相同地址的关键码 归于同一子集合,每一个子集合称为一个桶,各个桶中的元素通过一个单链表链接起来,各链表的头结点存储在哈希表中。
从上图可以看出,开散列中每个桶中放的都是发生哈希冲突的元素。
2. 开散列实现
namespace OpenHash
{
template
class HashNode
{
public:
HashNode(const std::pair kv)
:_kv(kv)
,_next(nullptr)
{
}
std::pair _kv;
HashNode* _next;
};
template>
class HashTable
{
public:
typedef HashNode Node;
HashNode* find(const K& key)
{
HashFunc hf;
if (_tables.size() == 0)
return nullptr;
size_t index = hf(key) % _tables.size();
if (_tables[index] == nullptr)
return nullptr;
HashNode* cur = _tables[index];
while (cur != nullptr)
{
if (cur->_kv.first == key)
return cur;
cur = cur->_next;
}
return nullptr;
}
bool erase(const K& key)
{
if (_tables.empty())
return false;
HashFunc hf;
size_t index = hf(key) % _tables.size();
Node* prev = nullptr;
Node *cur = _tables[index];
while (cur != nullptr)
{
if (cur->_kv.first == key)
{
if (prev == nullptr)
{
_tables[index] = cur->_next;
}
else
{
prev->_next = cur->_next;
}
delete cur;
break;
}
prev = cur;
cur = cur->_next;
}
--_n;
return true;
}
bool insert(const std::pair& kv)
{
HashNode* ret = find(kv.first);
if (ret != nullptr)
return false;
HashFunc hf;
if ( _n == _tables.size()) //扩容
{
//size_t newSize = _tables.size() == 0 ? 10 : _tables.size() * 2;
size_t newSize = GetNextPrime(_tables.size());
std::vector NewVector;
NewVector.resize(newSize);
for (size_t i = 0; i < _tables.size(); ++i)
{
Node* cur = _tables[i];
while (cur != nullptr)
{
Node* next = cur->_next;
size_t index = hf(cur->_kv.first) % NewVector.size();
cur->_next = NewVector[index];
NewVector[index] = cur;
cur = next;
}
_tables[i] = nullptr;
}
_tables.swap(NewVector);
}
size_t index = hf(kv.first) % _tables.size();
Node* newnode = new Node(kv);
newnode->_next = _tables[index];
_tables[index] = newnode;
++_n;
return true;
}
private:
std::vector _tables;
size_t _n = 0; //有效数据个数
};
void OpenHashTest()
{/*
HashTable ht;
int array[] = { 2,12,22,32,42,52,62,72,82 };
for (const auto &e : array)
{
ht.insert(std::make_pair(e, e));
}
ht.insert(std::make_pair(92, 92));
ht.insert(std::make_pair(102, 102));
ht.erase(22);
ht.erase(32);
ht.erase(42);
ht.erase(52);*/
HashTable ht;
ht.insert(std::make_pair("sort", "排序"));
ht.insert(std::make_pair("map", "地图"));
ht.insert(std::make_pair("left", "左边"));
ht.insert(std::make_pair("right", "右边"));
ht.insert(std::make_pair("apples", "苹果"));
}
} 3. 开散列增容
桶的个数是一定的,随着元素的不断插入,每个桶中元素的个数不断增多,极端情况下,可能会导致一 个桶中链表节点非常多,会影响的哈希表的性能,因此在一定条件下需要对哈希表进行增容,那该条件 怎么确认呢?开散列最好的情况是:每个哈希桶中刚好挂一个节点,再继续插入元素时,每一次都会发 生哈希冲突,因此,在元素个数刚好等于桶的个数时,可以给哈希表增容。
if ( _n == _tables.size()) //扩容
{
//size_t newSize = _tables.size() == 0 ? 10 : _tables.size() * 2;
size_t newSize = GetNextPrime(_tables.size());
std::vector NewVector;
NewVector.resize(newSize);
for (size_t i = 0; i < _tables.size(); ++i)
{
Node* cur = _tables[i];
while (cur != nullptr)
{
Node* next = cur->_next;
size_t index = hf(cur->_kv.first) % NewVector.size();
cur->_next = NewVector[index];
NewVector[index] = cur;
cur = next;
}
_tables[i] = nullptr;
}
_tables.swap(NewVector);
} 4. 开散列的思考
1. 只能存储 key 为整形的元素,其他类型怎么解决?
template
class Hash //如果是整型直接用自身做key
{
public:
size_t operator()(const K& key)
{
return key;
}
};
template<> //提供特化版本
class Hash
{
public:
size_t operator()(const std::string& key)
{
size_t value = 0;
for (const auto& e : key)
{
value *= 31; //通过数学推理得到的,可以31,131等。
value += e;
}
return value;
}
}; 2. 除留余数法,最好模一个素数,如何每次快速取一个类似两倍关系的素数?
static const unsigned long __stl_prime_list[28] =
{
53, 97, 193, 389, 769,
1543, 3079, 6151, 12289, 24593,
49157, 98317, 196613, 393241, 786433,
1572869, 3145739, 6291469, 12582917, 25165843,
50331653, 100663319, 201326611, 402653189, 805306457,
1610612741, 3221225473, 4294967291
};
static size_t GetNextPrime(size_t num)
{
for (size_t i = 0; i < 28; ++i)
{
if (__stl_prime_list[i] > num)
return __stl_prime_list[i];
}
return __stl_prime_list[27];
}
字符串哈希算法
5. 开散列与闭散列比较
应用链地址法处理溢出,需要增设链接指针,似乎增加了存储开销 。事实上: 由于开地址法必须保持大 量的空闲空间以确保搜索效率,如二次探查法要求装载因子 a <= 0.7 ,而表项所占空间又比指针大的 多,所以使用链地址法反而比开地址法节省存储空间
3. 模拟实现
3.1 哈希表的改造
#pragma once
#pragma once
#include
#include
template
class Hash
{
public:
size_t operator()(const K& key)
{
return key;
}
};
template<>
class Hash
{
public:
size_t operator()(const std::string& key)
{
size_t value = 0;
for (const auto& e : key)
{
value *= 31;
value += e;
}
return value;
}
};
static const unsigned long __stl_prime_list[28] =
{
53, 97, 193, 389, 769,
1543, 3079, 6151, 12289, 24593,
49157, 98317, 196613, 393241, 786433,
1572869, 3145739, 6291469, 12582917, 25165843,
50331653, 100663319, 201326611, 402653189, 805306457,
1610612741, 3221225473, 4294967291
};
static size_t GetNextPrime(size_t num)
{
for (size_t i = 0; i < 28; ++i)
{
if (__stl_prime_list[i] > num)
return __stl_prime_list[i];
}
return __stl_prime_list[27];
}
namespace OpenHash
{
template
class HashNode
{
public:
HashNode(const T & data)
:_data(data)
, _next(nullptr)
{
}
T _data;
HashNode* _next;
};
template //需要提前声明
class HashTable;
template
class HashTableIterator
{
public:
typedef HashNode Node;
typedef HashTableIterator Self;
HashTableIterator(Node* node, HashTable* pht)
:_node(node)
,_pht(pht)
{
}
Ref operator*()
{
return _node->_data;
}
Ptr operator->()
{
return &_node->_data;
}
Self& operator++()
{
if (_node->_next != nullptr) //说明当前桶还没走完
{
_node = _node->_next;
}
else
{
HashFunc hf;
KeyOfT kot;
size_t index = hf(kot(_node->_data)) % _pht->_tables.size(); //这里指针访问不了私有成员,可以用友元
++index;
while (index < _pht->_tables.size())
{
if (_pht->_tables[index] != nullptr)
{
break;
}
else
{
++index;
}
}
//走到有两中情况
if (index == _pht->_tables.size())
{
_node = nullptr;
}
else
{
_node = _pht->_tables[index];
}
}
return *this;
}
bool operator!=(const Self& s)
{
return _node != s._node;
}
bool operator==(const Self& s)
{
return _node == s._node;
}
private:
Node* _node;
HashTable* _pht;
};
template>
class HashTable
{
public:
typedef HashNode Node;
typedef HashTableIterator iterator;
template
friend class HashTableIterator; //声明友元
/*HashTable() //需要在初始化列表初始化vector和_n;所以需要提供默认构造
{
}*/
HashTable() = default; // c++11
HashTable(const HashTable& s)
{
_tables.resize(s._tables.size());
for (size_t i = 0; i < s._tables.size(); ++i)
{
Node* cur = s._tables[i];
while (cur != nullptr)
{
Node* copy = new Node(cur->_data);
copy->_next = _tables[i];
_tables[i] = copy;
cur = cur->_next;
}
}
}
HashTable& operator=(HashTable s)
{
swap(_n, s._n);
_tables.swap(s._tables);
return *this;
}
iterator begin()
{
for (size_t i = 0; i < _tables.size(); ++i)
{
if (_tables[i] != nullptr)
return iterator(_tables[i], this); //把表指针传递过去
}
return end();
}
iterator end()
{
return iterator(nullptr, this);
}
iterator find(const K& key)
{
HashFunc hf;
KeyOfT kot;
if (_tables.size() == 0)
return end();
size_t index = hf(key) % _tables.size();
if (_tables[index] == nullptr)
return end();
HashNode* cur = _tables[index];
while (cur != nullptr)
{
if (kot(cur->_data) == key)
return iterator(cur,this);
cur = cur->_next;
}
return end();
}
bool erase(const K& key)
{
if (_tables.empty())
return false;
HashFunc hf;
size_t index = hf(key) % _tables.size();
Node* prev = nullptr;
Node* cur = _tables[index];
while (cur != nullptr)
{
if (kot(cur->_data) == key)
{
if (prev == nullptr)
{
_tables[index] = cur->_next;
}
else
{
prev->_next = cur->_next;
}
delete cur;
break;
}
prev = cur;
cur = cur->_next;
}
--_n;
return true;
}
std::pair insert(const T& data)
{
KeyOfT kot;
//HashNode* ret = find(kot(data));
iterator ret = find(kot(data));
if (ret != end())
return std::make_pair(ret,false);
HashFunc hf;
if (_n == _tables.size()) //扩容
{
//size_t newSize = _tables.size() == 0 ? 10 : _tables.size() * 2;
size_t Newsize = GetNextPrime(_tables.size()); //根据STL源码库扩容都是素数
std::vector NewVector;
NewVector.resize(newSize);
for (size_t i = 0; i < _tables.size(); ++i)
{
Node* cur = _tables[i];
while (cur != nullptr)
{
Node* next = cur->_next;
size_t index = hf(kot(cur->_data)) % NewVector.size();
cur->_next = NewVector[index];
NewVector[index] = cur;
cur = next;
}
_tables[i] = nullptr;
}
_tables.swap(NewVector);
}
size_t index = hf(kot(data)) % _tables.size();
Node* newnode = new Node(data);
newnode->_next = _tables[index];
_tables[index] = newnode;
++_n;
return std::make_pair(iterator(newnode, this), true);
}
private:
std::vector _tables;
size_t _n = 0; //有效数据个数
};
} 3.2 unordered_map
#pragma once
#pragma once
#include"Hash.hpp"
namespace OpenHash
{
template> //这里第四个模板参数我就不想写了
class unodered_map
{
public:
class MapOfT
{
public:
const K& operator()(const std::pair & kv)
{
return kv.first;
}
};
typedef typename HashTable, MapOfT, hash>::iterator iterator;
iterator begin()
{
return _ht.begin();
}
iterator end()
{
return _ht.end();
}
std::pair insert(const std::pair& kv)
{
return _ht.insert(kv);
}
iterator find(const K& key)
{
return _ht.find(key);
}
bool erase(const K& key)
{
return _ht.erase(key);
}
private:
HashTable, MapOfT, hash> _ht;
};
void unordered_map_test()
{
/*unodered_map um;
um.insert(std::make_pair(1, 1));
um.insert(std::make_pair(11, 11));
um.insert(std::make_pair(21, 21));
um.insert(std::make_pair(31, 31));
um.insert(std::make_pair(41, 41));
um.insert(std::make_pair(51, 51));*/
unodered_map um;
um.insert(std::make_pair("sort", "排序"));
um.insert(std::make_pair("map", "地图"));
um.insert(std::make_pair("left", "左边"));
um.insert(std::make_pair("right", "右边"));
auto it = um.begin();
while (it != um.end())
{
std::cout << it->first << ":" << it->second << std::endl;
++it;
}
std::cout << std::endl;
unodered_map < std::string, std::string > um2 = um;
auto rit = um2.begin();
while (rit != um2.end())
{
std::cout << rit->first << ":" << rit->second << std::endl;
++rit;
}
}
}
3.3 unordered_set
#pragma once
#include"Hash.hpp"
namespace OpenHash
{
template>
class unordered_set
{
public:
class SetOfT
{
public:
const K& operator()(const K& key)
{
return key;
}
};
typedef typename HashTable::iterator iterator;
iterator begin()
{
return _ht.begin();
}
iterator end()
{
return _ht.end();
}
std::pair insert(const K& key)
{
return _ht.insert(key);
}
bool earse(const K& key)
{
return _ht.erase();
}
iterator find(const K& key)
{
return _ht.find(key);
}
private:
HashTable _ht;
};
void test_unordered_set()
{
//unordered_set us;
/*us.insert(4);
us.insert(14);
us.insert(34);
us.insert(7);
us.insert(24);
us.insert(17);*/
unordered_set < std::string> us;
us.insert("sort");
us.insert("map");
us.insert("left");
us.insert("right");
us.insert("apples");
}
}