动手学深度学习之多层感知机

多层感知机(MLP)是早期就出现的神经网络，拥有一层隐藏层，但由于没有非线性的激活函数，即使2层也只是做线性映射，功效与单层输出的神经网络差不多，本节将介绍MLP的基本概念以及如何解决MLP存在的缺陷。

MLP

1. 隐藏层
   
   形式化如下：
   $$\begin{gathered} H=X{W}_h+B_h \\ O=H{W}_o+B_o=X{W}_h{W}_o+B_h{W}_o+B_o \end{gathered}$$
   从公式可以看出，虽然神经网络引入了隐藏层，却依然等价于一个单层神经网络。要解决这个问题，需要引入激活函数，做非线性映射。
2. 激活函数
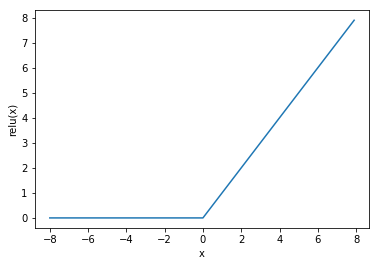
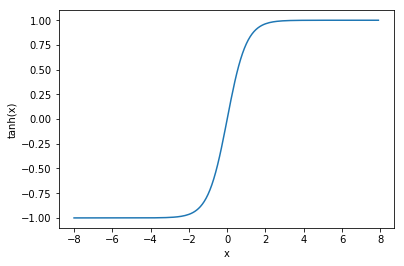
   常见的3个激活函数：ReLU/Sigmoid/tanh
   $ReLU(x)=max(x,0)$
   
   $Sigmoid(x)=\frac{1}{1+e^{-x}}$
   
   $tanh(x)=\frac{1-e^{-2x}}{1+e^{-2x}}$
   
3. MLP
   改进后的MLP就是含有至少一个隐藏层的由全连接层组成的神经网络，且每个隐藏层的输出都要通过非线性的激活函数进行变换。

从0实现

1. 加载数据集

import torch
import numpy as np
import sys
sys.path.append("/home/kesci/input")
import d2lzh1981 as d2l
print(torch.__version__)

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size,root='/home/kesci/input/FashionMNIST2065')

2. 初始化参数

num_inputs, num_outputs, num_hiddens = 784, 10, 256

W1 = torch.tensor(np.random.normal(0, 0.01, (num_inputs, num_hiddens)), dtype=torch.float)
b1 = torch.zeros(num_hiddens, dtype=torch.float)
W2 = torch.tensor(np.random.normal(0, 0.01, (num_hiddens, num_outputs)), dtype=torch.float)
b2 = torch.zeros(num_outputs, dtype=torch.float)

params = [W1, b1, W2, b2]
for param in params:
    param.requires_grad_(requires_grad=True)

3. 定义模型

def relu(X):
    return torch.max(input=X, other=torch.tensor(0.0))
    
def net(X):
    X = X.view((-1, num_inputs))
    H = relu(torch.matmul(X, W1) + b1)
    return torch.matmul(H, W2) + b2

4. 定义损失函数

loss = torch.nn.CrossEntropyLoss()

5. 定义优化函数

   SGD函数

6. 训练模型并预测

num_epochs, lr = 5, 100.0
def train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size,
              params=None, lr=None, optimizer=None):
    for epoch in range(num_epochs):
        train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
        for X, y in train_iter:
            y_hat = net(X)
            l = loss(y_hat, y).sum()
            
            # 梯度清零
            if optimizer is not None:
                optimizer.zero_grad()
            elif params is not None and params[0].grad is not None:
                for param in params:
                    param.grad.data.zero_()
            
            l.backward()
            if optimizer is None:
                d2l.sgd(params, lr, batch_size)
            else:
                optimizer.step()  # “softmax回归的简洁实现”一节将用到
            
            
            train_l_sum += l.item()
            train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item()
            n += y.shape[0]
        test_acc = evaluate_accuracy(test_iter, net)
        print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
              % (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))

d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, params, lr)

pytorch实现

import torch
from torch import nn
from torch.nn import init
import numpy as np
import sys
sys.path.append("/home/kesci/input")
import d2lzh1981 as d2l

print(torch.__version__)

num_inputs, num_outputs, num_hiddens = 784, 10, 256
    
net = nn.Sequential(
        d2l.FlattenLayer(),
        nn.Linear(num_inputs, num_hiddens),
        nn.ReLU(),
        nn.Linear(num_hiddens, num_outputs), 
        )
    
for params in net.parameters():
    init.normal_(params, mean=0, std=0.01)
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size,root='/home/kesci/input/FashionMNIST2065')
loss = torch.nn.CrossEntropyLoss()

optimizer = torch.optim.SGD(net.parameters(), lr=0.5)

num_epochs = 5
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, None, None, optimizer)

有话要说

一些问题：

1. 激活函数的作用？三种激活函数的优缺点？如何选择合适的激活函数？
2. 多层感知机就是指仅有一个隐藏层的神经网络吗？