算法学习day42

1. 01背包问题 二维

1.1 分析

动规五部曲：
1.确定dp数组以及下标的含义
使用二维数组：dp[i] [j]表示从下标为[0-i]的物品里面任取，放进容量为j的背包，价值总和最大是多少。

2.确定递推公式
dp[i] [j] :从下标为[0-i]的物品里任取，放进容量为j的背包，价值总和最大是多少。
不放物品i : dp[i-1] [j]，背包容量为j，放不进i。此时dp[i] [j] 就是dp[i-1] [j] 。

放物品i : 由dp[i-1] [j - weight[i]] 推出，dp[i - 1] [j- weight[i]] 容量为j - weight[i]的时候不放i的最大价值，现在要放i，即dp[i-1] [j - weight[i]] + value[i]。

递推公式: dp[i] [j] = max(dp[i - 1] [j], dp[i-1] [j -weight[i]] + value[i])。

3.dp数组如何初始化
由dp[i] [j] 的定义出发，当背包容量j为0的时候，背包价值总和一定为0.

dp[0] [j]:存放编号0物品的时候，各个容量的背包所能存放的最大价值。

当j < weight[0] 即背包容量比编号0的重量小，放不进。dp[0] [j]为0.

当j >= weight[0]即背包容量大于编号0的重量，可以放。dp[0] [j] == value[0]

// 存放0号物品时，发现背包比0号物品小，放不进。取0
for(int j = 0 ; j < weight[0]; j++){
    dp[0][j] = 0;
}
// 放0号物品，发现此时背包比0号物品大，放进去。值为0号物品的价值
for(int j = weight[0]; j<=bagweight; j++){
    dp[0][j] = value[0];
}

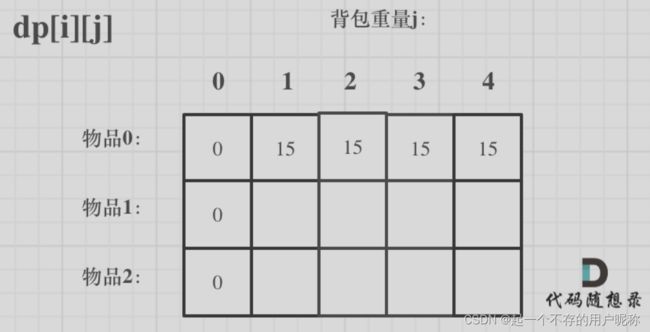
由递推公式：dp[i] [j] = max(dp[i - 1] [j],dp[i - 1] [ j -weight[i]]+value[i])，可知dp[i] [j]由上方和左上方推出。其他下标随便初始，最后会给赋值。

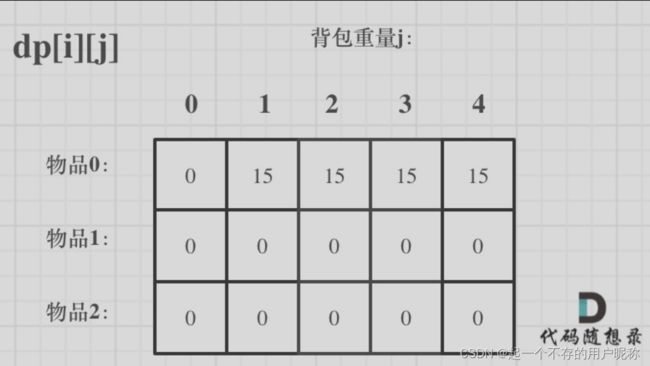
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
for(int j = weight[0]; j<= bagweight; j++){
    dp[0][j] = value[0];
}

4.确定遍历顺序
有两个遍历维度：物品与背包重量

先遍历物品再遍历背包重量

// weight 数组的大小，就是物品的个数
for(int i = 1; i< weight.size() ; i++){// 遍历物品
    for(int j = 0; j <=bagweight; j++){// 遍历背包容量
        if( j < weight[i]) dp[i][j] = dp[i-1][j];
        else dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);
    }
}

5.举例推导dp数组

1.2 代码

void test_2_wei_bag_problem1(){
    // 物品重量和价值
    vector<int> weight ={1, 3, 4};
    vector<int> value = {15, 20, 30};
    // 背包容量
    int bagweight = 4;
    
    // 创建一个二维数组来存储状态转移方程的值
    // dp[i][j] 表示当背包容量为 j 时前 i 个物品的最大价值
    vector<vector<int>> dp(weight.size(), vector<int>(bagweight+1 , 0));

    // 处理第一个物品
    // 当背包容量比第一个物品的重量小，无法放入
    for(int j = 0; j< weight[0]; j++){
        dp[0][j] = 0;
    }
    // 当背包容量比第一个物品的重量大，可以放入
    for(int j = weight[0]; j<=bagweight; j++){
        dp[0][j] =value[0];
    }
    
    // 从第二个物品开始遍历
    for(int i = 1; i<weight.size(); i++){  // 遍历物品
        for(int j = 0 ; j<=bagweight; j++){// 遍历背包容量
            // 如果当前物品的重量大于背包容量，则不能放入该物品
            if(j<weight[i]) dp[i][j]=dp[i-1][j];
            else {
                // 如果可以放入该物品，则有两种情况：
                // 1. 放入该物品后的价值比不放入该物品的价值更大
                // 2. 不放入该物品的价值更大
                dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);
            }
        }
    }
    // 输出最大价值
    cout<<dp[weight.size()-1][bagweight]<<endl;
}

2. 01背包问题 一维

2.1 分析

动规五部曲：
1.确定dp数组以及下标的含义
在一维dp数组中dp[j]：容量为j的背包，所背的物品价值可以最大为dp[j]。

2.一维dp数组的递推公式
dp[j]可以通过dp[j-weight[i]]推导出来，dp[j-weight[i]]：容量为j-weight[i]的背包所背的最大价值。

dp[j-weight[i]] + value[i] ：容量为j - 物品i重量，加上物品i的价值。

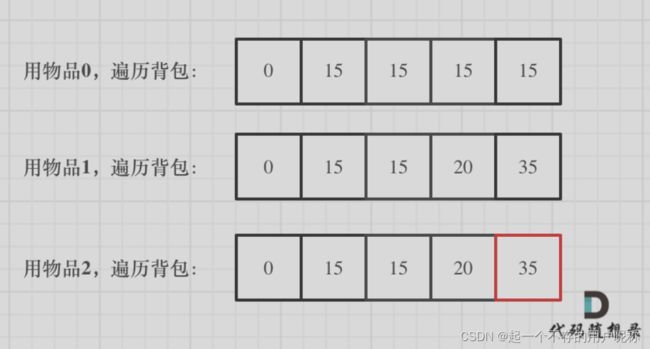
递推公式：dp[j] = max(dp[j], dp[j - weight[i]]+ value[i])

3.一维dp数组如何初始化
dp数组初始化为0

4.一维dp数组遍历顺序

for(int i = 0 ; i < weight.size() ; i++){      // 遍历物品
    for(int j = bagWeight; j >=weight[i]; j--){// 遍历背包容量
        dp[j] = max(dp[j],dp[j-weight[i]]+ value[i]);
    }    
}

5.举例推导dp数组

2.2 代码

void test_1_wei_bag_problem(){
    // 物品重量和价值
    vector<int> weight = {1,3,4};
    vector<int> value = {15, 20,30};
    // 背包容量
    int bagWeight = 4;
    
    // 创建一个一维数组来存储状态转移方程的值
    // dp[j] 表示当背包容量为 j 时的最大价值
    vector<int> dp(bagWeight + 1, 0);

    // 遍历每个物品
    for(int i = 0 ; i< weight.size() ; i++){
        // 倒序遍历背包容量
        // 这里使用倒序遍历的原因是为了避免当前物品重量和背包容量相等的情况
        for(int j = bagWeight; j>=weight[i]; j--){
            // 如果当前物品的重量大于背包容量，则不能放入该物品，维持上一个物品的价值
            // 否则，取当前物品放入背包和不放入背包的两种情况中的最大值作为当前背包容量的最大价值
            dp[j] = max(dp[j],dp[j-weight[i]]+ value[i]);
        }
    }
    // 输出最大价值
    cout<<dp[bagWeight]<<endl;
}

3. 力扣416. 分割等和子集

3.1 分析

动规五部曲：
1.确定dp数组以及下标的含义
01背包中，dp[j]表示：容量为j的背包，所背的物品价值最大可以为dp[j]。

dp[j]表示背包总容量。

2.确定递推公式

01背包的递推公式为：dp[j] = max(dp[j],dp[j-weight[i]]+value[i])

本题物品i的重量时nums[i]，价格也是nums[i]。

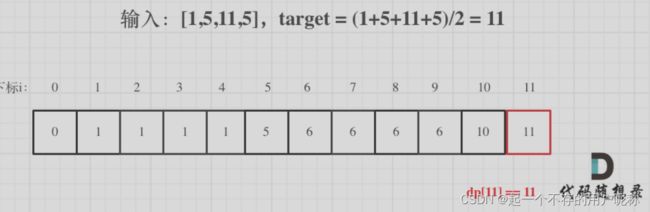
递推公式:dp[j] = max(dp[j], dp[j - nums[i]]+ nums[i])

3.dp数组如何初始化

本题：只包含正整数的非空数组，所以非0下标的元素初始化为0即可。

// 题目中说：每个数组中的元素不会超过 100，数组的大小不会超过 200
// 总和不会大于20000，背包最大只需要其中一半，所以10001大小就可以了
vector<int> dp(10001, 0);

4.确定遍历顺序

for(int i =0; i < nums.size() ; i++){
    for(int j = target; j >=nums[i] ; j--){// 每一个元素一定是不可重复放入的，所以从大到小遍历
        dp[j] = max(dp[j],dp[j-nums[i]]+ nums[i]);
        
    }
}

5.举例推导dp数组

3.2 代码

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        // 计算数组总和
        int sum = 0;
        for(int i = 0; i < nums.size(); i++){
            sum += nums[i];
        }
        // 如果总和为奇数，则不能划分为两个和相等的子集
        if(sum % 2 == 1) return false;
        // 计算背包容量，也就是要达到的目标和
        int target = sum / 2;
        
        // 创建一个一维数组来存储状态转移方程的值
        // dp[j] 表示当背包内元素总和为 j 时的最大价值
        vector<int> dp(target+1, 0);
        
        // 遍历每个数
        for(int i = 0; i < nums.size() ; i++){
            // 倒序遍历背包容量
            // 这里使用倒序遍历的原因是为了避免当前元素和背包容量相等的情况
            for(int j= target; j>=nums[i]; j--){
                // 如果当前元素的值大于背包容量，则不能放入该元素，维持上一个元素的价值
                // 否则，取当前元素放入背包和不放入背包的两种情况中的最大值作为当前背包容量的最大价值
                dp[j] = max(dp[j],dp[j-nums[i]]+nums[i]);
            }
        }
        
        // 如果背包容量等于目标和，则可以划分为两个和相等的子集
        if(dp[target] == target) return true;
        return false;
    }
};

4.参考资料

[代码随想录]