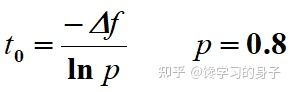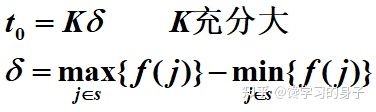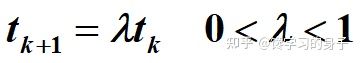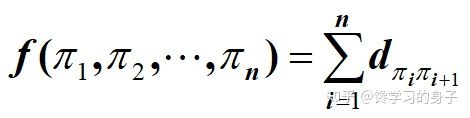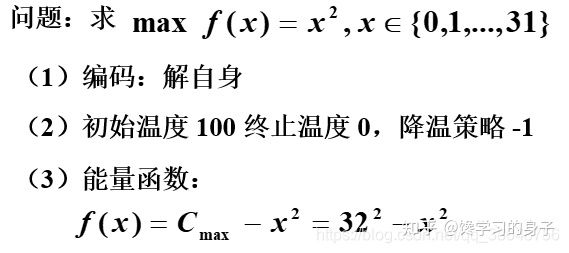模拟退火算法

1.算法简介

模拟退火算法（Simulated Annealing，SA）是一种模拟物理退火的过程而设计的随机优化算法，结合爬山法和随机行走算法，同时避免算法进入局部最优，早期用于组合优化，后来发展成一种通用的优化算法。它的基本思想最早在1953年就被Metropolis提出，但直到1983年Kirkpatrick等人才设计出真正意义上的模拟退火算法并进行应用。

该算法采用类似于物理退火的过程，先在一个高温状态下（相当于算法随机搜索），然后逐渐退火，在每个温度下（相当于算法的每一次状态转移），徐徐冷却（相当于算法局部搜索），最终达到物理基态（相当于算法找到最优解）。

高温过程——增强粒子的热运动，使其偏离平衡位置，目的是消除系统原先可能存在的非均匀态； 等温过程——退火过程中要让温度慢慢降低，在每一个温度下要达到热平衡状态，对于与环境换热而温度不变的封闭系统满足自由能较少定律，系统状态的自发变化总是朝自由能减少的方向进行，当自由能达到最小时，系统达到平衡态； 冷却过程——使粒子热运动减弱并渐趋有序，系统能量逐渐下降，从而得到低能的晶体结构。当液体凝固为固体的晶态时退火过程完成。

因此模拟退火算法从某一高温出发，在高温状态下计算初始解，然后以预设的邻域函数产生一个扰动量，从而得到新的状态，即模拟粒子的无序运动，比较新旧状态下的能量，即目标函数的解。如果新状态的能量小于旧状态，则状态发生转化；如果新状态的能量大于旧状态，则以Metropolis接受准则发生转化。当状态稳定后，便可以看作达到了当前状态的最优解，便可以开始降温，在下一个温度继续迭代，最终达到低温的稳定状态，便得到了模拟退火算法产生的结果

该算法的关键点如下： 1、对固体退火过程的模拟； 2、采用Metropolis接受准则； 3、用冷却进度表控制算法进程，使算法在多项式时间里给出一个近似解。 固体退火过程是SAA的物理背景；Metropolis接受准则使算法跳离局部最优 “险井”；而冷却进度表的合理选择是算法应用的前提。

下面依次介绍上述三个关键点

1.1 固体退火过程：

对于该部分如果不理解，可以先简单跳过。 固体退火过程的数学表述： 在温度T，分子停留在状态r满足Boltzmann概率分布

温度低时能量低的微观状态概率大，温度趋于零时，固体几乎处于概率最大、能量最小的基态。 在同一个温度T，选定两个能量E1

因此，在同一个温度，分子停留在能量小的状态的概率比停留在能量大的状态的概率要大。

1.2 Metropolis准则

Metropolis准则（1953）——以概率接受新状态，固体在恒定温度下达到热平衡的过程可以用Monte Carlo方法（计算机随机模拟方法）加以模拟。

Monte Carlo模拟退火过程：蒙特卡罗(Monte Carlo)方法，或称计算机随机模拟方法，是一种基于“随机数”的计算方法。

若在温度T，当前状态i → 新状态j 若Ej

可以看出，高温下可接受与当前状态能差较大的状态为重要状态，而在低温下只能接受与当前状态能差较小的新状态为重要状态。在温度趋于零时，就不再接受Ej>Ei的新状态j了.如此反复，达到系统在此温度下的热平衡。这个过程称作Metropolis抽样过程。上面这种方法被称为重要性采样法，该方法以概率形式接受新状态，避免局部最优。

1.3 冷却进度表

在Metropolis抽样过程中温度T缓慢的降低，模拟退火过程就是通过T参数的变化使状态收敛于最小能量处。因而，T参数的选择对于算法最后的结果有很大影响。初始温度和终止温度设置的过低或过高都会延长搜索时间。降温步骤太快，往往会漏掉全局最优点，使算法收敛至局部最优点。降温步骤太慢，则会大大延长搜索全局最优点的计算时间，从而难以实际应用。因此选择一个合适的降温函数非常重要，冷却进度表就是指的从某一高温状态T向低温状态冷却时的降温函数。

对物理退火过程和模拟退火算法进行一个简单的对比：

2.算法流程

有了上面对该算法基础的理解后，下面对算法的流程进行介绍：

可以看出该算法有内外两次循环，内循环用来模拟同一温度下多次的状态转移，也称为抽样稳定准则（为什么称为“抽样稳定”准则，我的理解是等温过程在邻域选择下一次状态转移，一般需要在邻域内采样多次，进行多次状态转移，进而达到这一温度下的稳定状态），外循环作为算法终止准则。 另外其中有3个比较重要的函数，分别为状态产生函数（邻域函数），状态接受函数，退温函数。同时另外还需注意到一个关键部分就是初温、初始解的初始化。下面对上述内容展开介绍：

2.1 状态产生函数（邻域函数）

设计的出发点：尽可能保证产生的候选解遍布全部解空间。该函数包括两部分的内容：产生候选解的方式、候选解产生的概率分布。前者决定由当前解产生候选解的方式，后者决定在当前解产生的候选解中选择不同状态的概率。

候选解的产生方式由问题的性质决定，通常在当前状态的邻域结构内以一定概率方式产生，而邻域函数和概率方式可以多样化设计，其中概率分布可以是均匀分布、正态分布、指数分布、柯西分布等。

2.2 状态接受函数

状态接受函数的目的是尽可能接受优化解，状态接受函数一般以概率的方式给出，不同接受函数的差别主要在于接受概率的形式不同，设计状态接受概率，应遵循的原则： - 固定温度下，接受使目标函数值下降的候选解的概率要大于使目标函数值上升的候选解的概率。 - 随温度的下降，接受使目标函数值上升的解的概率要逐渐减小。 - 当温度趋于零时，只能接受目标函数值下降的解。

下面为标准形式下的状态接受概率，通过将该概率与[0,1]之间的随机数进行比较，从而决定是否接受该候选解

2.3 初温

实验表明：初温值只要选择充分大，获得高质量解的概率就大！但花费计算时间增加。 因此，初温的选择要足够高。初温的确定应折衷考虑优化质量和优化效率，有以下两种方式： - 均匀抽样一组状态，选各状态目标值的方差 - 利用经验公式 a.随机产生一组状态，确定两两状态间的最大目标值差，然后依据差值，利用一定的函数确定初温。例如

b.

2.4 温度更新函数

温度更新函数即温度的下降方式，用于在外循环中修改温度值，衰减量“以小为宜”。

实验表明降温速度越慢，获得高质量解的几率越大，但花费的计算时间将同时增加。因此可以使其温度高时下降的慢些，温度低时下降的快些。主要有以下几种方式： a.

Kirkpatrick首先提出对于lambd可选0.95，Johnson,Bonomi及Lutton采用[0.5,0.99].

b.Nahar及Skiscim等人把[0,$t_0$]划分成K个小区间，温度更新函数为

2.5 Metropolis抽样稳定准则

用于决定在各温度下产生候选解的数目($L_k$). 具体应与问题规模成比例。实验表明高温时迭代次数越多越好，低温时迭代次数可以适当减少。 在这里引入下马尔可夫链

马氏链模型：

时齐算法的收敛性：

结论1 时齐模拟退火算法对应的有限状态马氏链存在平稳分布。 结论2 当温度趋于0时，马氏链以概率1收敛到最优状态集，而收敛到非最优状态的概率为0。 实现途径：通过各温度下各状态序列无限长得以实现！

非时齐算法的收敛性：

对于非时齐算法

SA算法从某一个初始状态开始后，每一步状态转移均是在当前状态的邻域中随机产生新状态，然后以一定概率进行接受的。接受概率仅依赖于新状态和当前状态，并由温度加以控制。因此，SAA对应一个马氏链。

对于时齐算法，若固定每一温度，算法均计算马氏链的变化直至平稳分布，然后下降温度。 对于非时齐算法，若无需各温度下算法均达到平稳分布，但温度需按照一定的速率下降。或称非平稳马氏链算法。

马尔可夫链这部分我目前的理解还不是很深刻，后面有了认识后会加以补充。先记住下面的结论： 非时齐SAA：每个温度下只产生一个或少量候选解。 时齐算法——常用Metropolis抽样稳定准则包括： - 检验目标函数值的均值是否稳定 - 连续若干步目标函数值的变化较小 - 按一定的步数抽样

2.6 算法终止准则

用于决定算法何时结束。 理论上要求温度终值趋于零，通常的做法包括： - 设置终止温度的阀值 - 设置外循环迭代次数(6-50) - 算法搜索到的最优值连续若干步保持不变 - 检验系统熵是否稳定(==暂未理解==)

小结： 模拟退火算法基本要素和设定方法

3.算法示例

3.1 TSP问题

解空间：

目标函数：

初始解：

状态产生函数：新解的产生 互换操作(SWAP)：随机交换两个不同城市的位置。 逆序操作(INV)：两个不同随机位置的城市逆序。 插入操作(INS)：随机选择某个城市插入到不同随机位置。

初始温度的计算：

for i=1:100
         route=randperm(CityNum);
         fval0(i)=CalDist(dislist,route);
     end
     t0=-(max(fval0)-min(fval0))/log(0.9);

3.2 背包问题

已知背包的装载量为c=8，现有n=5个物品，它们的重量和价值分别是(2, 3, 5, 1, 4)和(2, 5, 8, 3, 6)。试使用模拟退火算法求解该背包问题，写出关键的步骤。 求解：假设问题的一个可行解用0和1的序列表示，例如i=(1010)表示选择第1和第3个物品，而不选择第2和第4个物品。用模拟退火算法求解此例的关键过程如图所示：

3.3 函数优化问题的求解

4.算法实现

下面以一个非常简单的例子进行算法实现，优化f(x)=$x^3-60x^2-4x+6$，求其在定义域[0,100]内的最小值

from __future__ import division
import numpy as np
import matplotlib.pyplot as plt
import math


# define aim function
def aimFunction(x):
    y = x ** 3 - 60 * x ** 2 - 4 * x + 6
    return y


x = [i / 10 for i in range(1000)]
y = [0 for i in range(1000)]
for i in range(1000):
    y[i] = aimFunction(x[i])

plt.plot(x, y)
T = 1000  # initiate temperature
Tmin = 10  # minimum value of terperature
x = np.random.uniform(low=0, high=100)  # initiate x
k = 50  # times of internal circulation
y = 0  # initiate result
t = 0  # time
while T >= Tmin:
    for i in range(k):
        # calculate y
        y = aimFunction(x)
        # generate a new x in the neighboorhood of x by transform function
        xNew = x + np.random.uniform(low=-0.055, high=0.055) * T
        if (0 <= xNew and xNew <= 100):
            yNew = aimFunction(xNew)
            if yNew - y < 0:
                x = xNew
            else:
                # metropolis principle
                p = math.exp(-(yNew - y) / T)
                r = np.random.uniform(low=0, high=1)
                if r < p:
                    x = xNew
    t += 1
    print(t)
    T = 1000 / (1 + t)  #降温函数，也可使用T=0.9T

print(x, aimFunction(x))

运行结果：

最小值大概在40左右，通过求导计算得到最小值为40.033，该模拟退火算法最终的计算结果如下

为寻找在有限时间逼近全局最优的模拟退火算法，设置了许多控制算法收敛的参数。在退火过程中指定了有限的退火温度值和在每一温度下的转移数目。Kirlpatrick等人在退火步骤中设定的参数如下： （1）初始温度值：初始温度值T0要选的足够高，保证模拟退火算法中所有可能的转移都能被接受。 （2）温度的下降：原先使用指数函数实现温度的下降。但是这种方法使降温幅度过小，从而延长搜索时间。在实际中，通常使用下式：

此处λ是一小于却接近于1的常数。λ通常的取值在0.8至0.99之间。 （3）终止温度：如果在连续的若干个温度下没有可接受的新状态，系统冻结或退火停止。

5.进阶

1.算法特点 可以保证全局最优特别适合组合优化问题，可以随机选择初始解，对问题本身没有特别要求，不会因为问题实例的改变影响性能，简单易行，通用性好。 模拟退火算法（SAA）在某一初温下，伴随温度参数的不断下降，结合概率突跳特性在解空间中随机寻找目标函数的全局最优解，即在局部最优解能概率性地跳出并最终趋于全局最优。

2.模拟退火算法在求解规模较大的实际问题时，往往存在以下缺点： （1）收敛速度比较慢。 （2）尽管理论上只要计算时间足够长，模拟退火法就可以保证以概率1收敛于全局最优点。但是在实际算法的实现过程中，由于计算速度和时间的限制，在优化效果和计算时间二者之间存在矛盾，因而难以保证计算结果为全局最优点，优化效果不甚理想。 （3）在每一温度下很难判定是否达到了平衡状态。 为此，人们对模拟退火算法提出了各种各样的改进，其中包括并行模拟退火算法、快速模拟退火算法（Cauchy机）和对模拟退火算法中各个函数和参数的重新设计等。

3.改进的可行方案 （1）设计合适的状态产生函数； （2）设计高效的退火历程； （3）避免状态的迂回搜索； （4）采用并行搜索结构； （5）避免陷入局部极小，改进对温度的控制方式； （6）选择合适的初始状态； （7）设计合适的算法终止准则。
改进的方式：增加某些新的环节 （1）增加升温或重升温过程，避免陷入局部极小； （2）增加记忆功能（记忆“Best so far”状态）； （3）增加补充搜索过程（以最优结果为初始解）； （4）对每一当前状态，采用多次搜索策略，以概率接受区域内的最优状态； （5）结合其它搜索机制的算法； （6）上述各方法的综合。
改进的思路 （1）记录“Best so far”状态，并即时更新； （2）设置双阈值，使得在尽量保持最优性的前提下减少计算量，即在各温度下当前状态连续 m1 步保持不变则认为Metropolis抽样稳定，若连续 m2 次退温过程中所得最优解不变则认为算法收敛。 改进的退火过程 （1）给定初温t0，随机产生初始状态s，令初始最优解s=s，当前状态为s(0)=s，i=p=0； （2）令t=ti，以t，s和s(i)调用改进的抽样过程，返回其所得最优解s’和当前状态s’(k)，令当前状态s(i)=s’(k)； （3）判断C(s)m2? 若是，则转第(6)步；否则，返回第(2)步； （6）以最优解s*作为最终解输出，停止算法。

改进的抽样过程 （1）令k=0时的初始当前状态为s’(0)=s(i)，q=0； （2）由状态s通过状态产生函数产生新状态s’，计算增量∆C’=C(s’)-C(s)； （3）若∆C’<0，则接受s’作为当前解，并判断C(s’)>C(s’)? 若是，则令s’=s’，q=0；否则，令q=q+1。若∆C’>0，则以概率exp(-∆C’/t)接受s’作为下一当前状态； （4）令k=k+1，判断q>m1? 若是，则转第(5)步；否则，返回第(2)步； （5）将当前最优解s*’和当前状态s’(k)返回改进退火过程。

时间不变的噪声算法（TINA Time-invariant noise algorithm） 状态产生函数中扰动强度不随时间改变，而是和能量大小相关，能量大的扰动大，能量小的扰动小，能量为零，扰动也为零，算法停止。

单调升温(Monotonic temperature rising) SA 在算法退火后期，温度很低且陷入局部极小解的时，算法很难跳出。因此，可以适当重新提高温度，促使算法跳出。

记忆指导SA(Simulated Annealing with Memmory Guidance ,简记为SAMG) 增加一个记忆装置，存储算法计算过程产生的最好的解，以这个解为最终解。

自适应SA算法 根据邻域搜索进展的反馈信息, 自适应确定温度变化和邻域搜索强度 特点： 1) 退火过程中温度参数变化符合幅值递减的下降总趋势, 但不排除局部升温的可能, 以保证寻求到合适的温度序列, 避免陷入局部最优; 2) 算法的终止条件依据退火温度和邻域搜索进展状态设计; 3) 每一温度下算法的迭代次数随温度下降而递增, 邻域搜索强度依其对目标函数的贡献动态分配; 4) 温度变化、邻域搜索和终止条件的控制机制由算法过程自动触发。

并行性 操作并行性：各个环节同时处理； 进程并行性：同时多个算法运行； 空间并行性：解空间分解分别处理，最终组合。

4.传统优化算法与全局优化算法的对比： 全局优化算法： 1、不依赖于初始条件； 2、不与求解空间有紧密关系，对解域，无可微或连续的要求。求解稳健，但收敛速度慢。能获得全局最优。适合于求解空间不知的情况 传统优化算法： 1、依赖于初始条件。 2、与求解空间有紧密关系，促使较快地收敛到局部解，但同时对解域有约束，如可微或连续。利用这些约束，收敛快。 3、有些方法，如Davison-Fletcher-Powell直接依赖于至少一阶导数；共轭梯度法隐含地依赖于梯度。

参考链接： https://blog.csdn.net/WFRainn/article/details/80303138 https://www.cnblogs.com/ranjiewen/p/6084052.html https://blog.csdn.net/To_be_to_