编程之法学习笔记——1.2字符串的包含

题目描述：

给定一长字符串a和一短字符串b。请问，如何最快地判断出短字符串b中的所有字符是否都在长字符串a中？请编写函数bool StringContain(string &a,string &b)实现此功能。为简单起见，假设输入的字符串只包含大写英文字母。

暴力轮询法：

设A、B字符串长度分别为m、n，使用两个指针i、j标识A、B字符串中位置。对A中全部字符，搜索B中j位置的字符是否出现，如出现，j位置后移一位，如未出现，直接返回false。该算法时间复杂度O(mn)，空间复杂度为O(1)。

#include 
#include 
using namespace std;
bool StringContain(string & a, string & b);

int main()
{
	cout << "Enter the long string: ";
	string longstr;
	cin >> longstr;
	cout << "Enter the short string: ";
	string shortstr;
	cin >> shortstr;
	cout << boolalpha << StringContain(longstr, shortstr);
	return 0;
}

bool StringContain(string & a, string & b)
{
	int i, j, ct = 0;
	for (j = 0; j < b.length(); j++)  //暴力轮询
	{
		for (i = 0; i < a.length(); i++)
		{
			if (a[i] == b[j])
			{
				ct++;  
				break;
			}
		}				
	}
	return (ct == b.length());  //如果ct=b.length，则b中全部元素均在a中出现
}

排序后轮询：

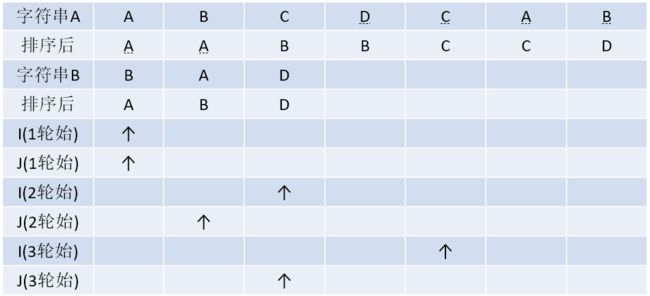
由于A、B字符串均是无序字符串，那么暴力轮询对于每一个B中字符，均要与a中全部字符进行比较，这导致A中字符被多次访问，导致时间浪费。为解决该问题，可以将A、B字符串均进行排序，得到两个有序字符串，对两有序字符串进行轮询可以保证A中字符不会被多次访问，大大减少访问时间。该算法采用C++自带sort()函数，排序所需时间复杂度O(nlogn)+O(mlogm)，轮询所需时间复杂度为O(m+n)，总时间复杂度为O(nlogn)，空间复杂度为O(1)。

#include  //使用sort()函数
bool StringContain(string & a, string & b)
{
	sort(a.begin(), a.end());
	sort(b.begin(), b.end());  //两字符串排序
	int i, j;
	for (i = 0, j = 0; j < b.length();)
	{
		while ((i < a.length()) && (a[i] < b[j]))
		{
			i++;  //保证i位置跳过重复字符
		}
		if (i >= a.length() || a[i] > b[j])
		{
			return false;  //i到达结尾仍未重复或a[i]>b[j]，此时b中字符未在a中出现
		}
		j++;  
	}
	return true;
}

素数相乘法：

对于字符串中包含的A~Z字符，将每个字符赋予一个独立的素数，计算整个A字符串各素数的乘积，对B字符串中每个字符，使用其对应的素数与A中乘积求余，如果存在余数，则说明该字符不在A字符串中。

(原理分析：设A_sum = n₁ * n₂ *…* n₂₆ ,设B[j]=n_x。由于任何两不同素数相除均存在余数，如果A_sum%B[j] = 0,则证明n_x一定为A_sum中的一个因数，那么B[j]一定存在于A字符串中。)

该算法只需计算出A中素数的乘积，然后使用B中每一个素数相除即可得到答案，时间复杂度为O(m+n)，空间复杂度为O(1)。但由于素数相乘结果很大，会超出long long类型的表示范围，故该方法不可行。

哈希表法：

将A中各个字符存在哈希表中(此处为方便编写，设哈希表长度为26，不需要考虑散列冲突问题)，对于B中各个字符，只需要查找该字符是否在哈希表中出现，即可判断B中字符是否在A字符串中出现。该算法时间复杂度为O(m+n)，空间复杂度为O(1)。

bool StringContain(string & a, string & b)
{
	int hash[26] = {0};  //构造简单哈希表
	for (int i = 0; i < a.length(); i++)
	{
		hash[(a[i] - 'A')] = 1;  //将出现的字符的哈希表位置置1
	}
	for (int i = 0; i < b.length(); i++)
	{
		if (hash[(b[i] - 'A')] == 0)  //判断B中字符是否在哈希表中出现
		{
			return false;
		}
	}
	return true;
}

位运算法：

位运算法本质上和哈希表法类似。哈希表法中通过开辟一个数组或链表存储A中各字符是否出现，而位运算法则使用一个整数来代表哈希表。如果A字符串中该字符出现，则将整数1左移对应的位数，并于原hash对应整数进行或运算。对B字符串中每一位，如果字符所对应的整数与hash进行与运算后不为0，则说明该字符在A字符串中出现。该算法时间复杂度O(n+m)，空间复杂度为O(1)。

例如A字符串为"ABCD",B字符串为"BAD".

1)计算A字符串的hash整数，'A':0001,'B':0010,'C':0100,'D':1000，则hash='1111';

2)将B字符串中所有字符与hash整数与运算.'B':0010,('B'&hash)=(0010)!=0，则说明'B'在A字符串中出现。

bool StringContain(string & a, string & b)
{
	int hash = 0;
	for (int i = 0; i < a.length(); i++)
		hash |= (1 << (a[i] - 'A'));  //二进制下，每个字符的最高位为1，其他位置均为0
	for (int i = 0; i < b.length(); i++)
	{
		if ((hash&(1 << b[i] - 'A')) == 0)  //B中字符所对应的整数是否在hash中出现
			return false;
	}
	return true;
}

课后习题：变位词

如果两个字符串中的字符一样，出现次数也一样，只是出现顺序不一样，则认为这两个字符串是兄弟字符串。现提供一个字符串，请问如何在字典中迅速找到它的兄弟字符串。

解法：

对于两个字符串是否为兄弟字符串，可以通过先对两字符串进行排序，对排序后结果进行比较，如果两排序后字符串相同，即可认为是兄弟字符串。现在问题在于如何在字典中进行查找？

bool StringContain(string & a, string & b)
{
	sort(a.begin(), a.end());
	sort(b.begin(), b.end());  //排序
	return (a == b);  //判断排序后是否相同
}