数据结构与算法系列-线性表-数组(线性表的推广)
转载自 重庆邮电大学计算机学院 PPT
数据元素可为结构类型的线性表
数组是由一组具有相同特征的数据元素的组成的.
如果数组元素只含有一个下标,则称为以为数组.若把数据元素的下标顺序变换成线性表的序号,则一维数组就是一个线性表.
如果每个元素有两个下标,则称为二维数组,一个 m x n的矩阵就是一个二维数组.
数组的ADT(抽象数据类型(Abstract Data Type))定义
ADT Array{
数据对象:
ji = 0,…,bi-1, i=1,2,…,n
D = {aj1j2…jn | n称为数组的维数,
bi是数组第i维的长度,
ji是数组元素的第i维下标,
aj1j2…jn ElemSet
R = {R1, R2, …, Rn} //每个元素受到n个关系的约束
Ri = {
0 jk bk-1, 1 k n 且 k i
0 ji bi-2,
aj1…ji…jn, aj1,,,ji+1…jn D, i = 2,…n}
P:
InitArray(&A, n, bound1, …, boundn)
DestoryArray(&A)
Value(A, &e, index1, …, indexn) //取出元素值
Assign(&A, e, index1, …, indexn) //给元素赋值
}ADT Array
数组的特点
数组中各元素都具有统一的类型
d维数组的非边界元素具有d个直接前趋和d个直接后继数组维数确定后,数据元素个数和元素之间的关系不再发生改变,适合于顺序存储
每组有定义的下标都存在一个与其相对应的值
数组的顺序表示
数组通常采用顺序存储方式来实现
n维数组的数据元素的存储问题
必须约定存放次序
因为存储单元是一维的,而数组是多维的
存储方案
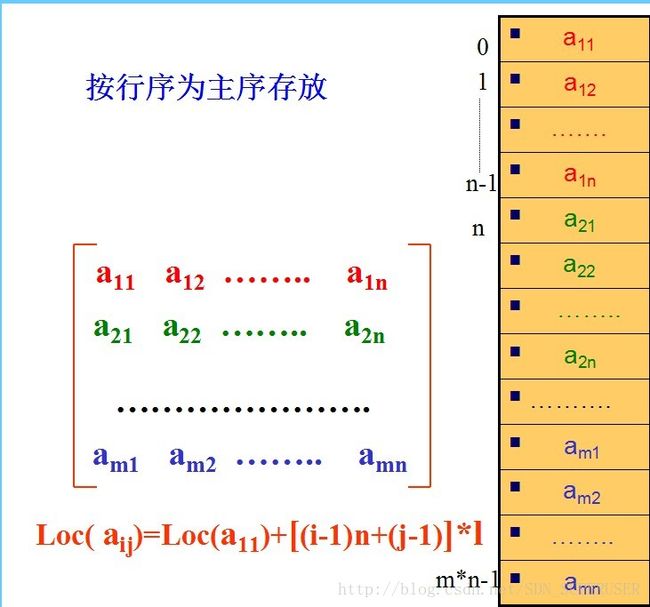
以行序为主序,如C, Pascal, Basic等语言采用
以列序为主序,如Fortran语言采用
数组一旦定义了维数和各维长度,便可为其分配存储空间
只要给出一组下标便可求得相应元素的存储位置
数据元素的存储问题
n维数组为例
如 int A[b1,b2 ,…,bn],共占用b1*b2 *…*bn个整型存储单元
行序为主序的存储方式
给定下标值j1, j2,…, jn , 求对应元素的存储位置
Loc(j1, j2,…, jn) = Loc(0, 0,…,0) + L *
(b2* …..*bn* j1 +
b3* …*bn* j2 +
… …
bn* jn-1 +
jn )
矩阵
矩阵的常见操作
转置、相乘等
void TransposeMatrix(int T[][], int M[][], mu, nu) {
//矩阵转置
for (col = 1; col <= nu; ++col)
for (row = 1; row <= mu; ++row)
T[col][row] = M[row][col];
}void ProductMartrix(int Q[][], int M[][], int N[][], m1, n1, n2) {
//矩阵相乘 Qm1*n2=Mm1*n1*Nm2*n2, n1=m2
for (i = 1; i <= m1; ++i)
for (j = 1; j <= n2; ++j) {
Q[i][j] = 0;
for (k = 1; k <= n1; ++k)
Q[i][j] += M[i][k] * N[k][j];
}
}矩阵的压缩存储
特殊矩阵值相同的元素或零元素在矩阵中的分布有规律
如对称矩阵,三角矩阵等
稀疏矩阵
值相同的元素或零元素在矩阵中的分布无规律,且
非零元素个数/矩阵所有元素个数 <= 0.05
矩阵的压缩存储
多个值相同的元素只分配一个存储空间
只存储非零元素
特殊矩阵的压缩存储
矩阵中的元素满足性质:aij = aji

对称矩阵压缩存储
为每一对对称元素分配一个存储空间,这样可将n*n个元素压缩存储到n*(n-1)/2个存储空间中
可选择存储其上三角(包括对角线)中的元素或其下三角(包括对角线)中的元素
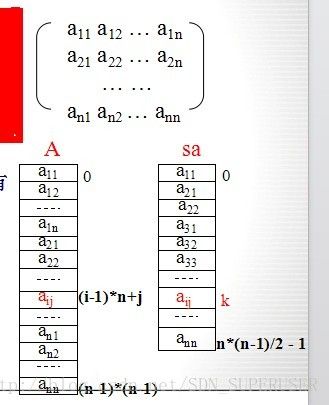
讨论以行序为主序的下三角矩阵的存储
若不采用压缩存储,矩阵需用二维数组A[n][n]存储若采用压缩存储,可采用一维数组sa[n*(n-1)/2]存储
元素sa[k]和矩阵元素aij之间有如下对应关系
i(i-1)/2 + j – 1 当 i >= j
k =
j(j-1)/2 + i – 1 当 i < j
压缩存放时,用一维数组存放,只需6个单元
如a32存放在sa[4]中
下(上)三角矩阵是指矩阵的上(下)三角(不包括对角线)中的元均为常数c或零的n阶矩阵
三角矩阵的压缩存储
只存储下(上)三角中的元素,再加一个存储常数c的空间即可
所有非零元素都集中在以主对角线为中心的带状区域中
对角矩阵的压缩存储
可按照某原则(或以行为主,或以对角线的顺序)将其压缩到一维数组中
稀疏矩阵的压缩存储
值相同的元素或零元素在矩阵中的分布无规律,且
非零元素个数/矩阵所有元素个数 <= 0.05
原理
只需存储矩阵中的非零元素所在的行号、列号和值
方法
三元组顺序表 (*)
行逻辑联接顺序表
十字链表
以顺序结构存储三元组表
#define MAXSIZE 12500 //假设非零元素个数的最大值
typedef struct{
int i, j; //行号,列号
ElemType e;//元素值
}Triple; //三元组
typedef struct{
Triple data[MAXSIZE + 1]; //非零元素三元组表,data[0]未用
int mu, nu, tu; //行数,列数,非零元素个数
}TSMatrix; //三元组顺序表
TSMatrix M; //矩阵M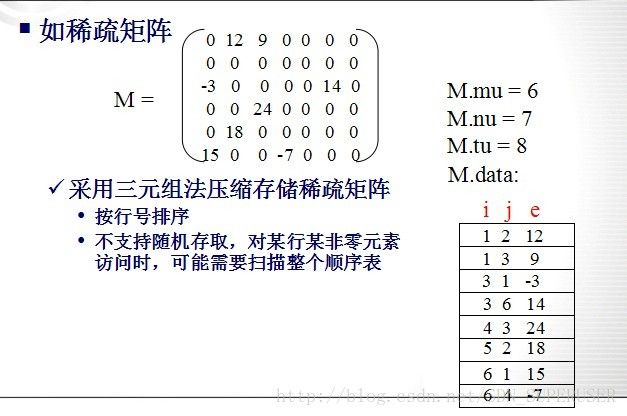
Status TransposeSMatrix(TSMatrix M, TSMatrix &T) {
T.mu = M.nu; T.nu = M.mu; T.tu = M.tu;
if (T.tu) { //有非零元素,转置
q = 1; //非零元素计数器
for (col = 1; col <= M.mu; ++col) //按列
for (p = 1; p <= M.tu; ++p) //在三元组中找
if (M.data[p].j = col) {
T.data[q].i = M.data[p].j;
T.data[q].j = M.data[p].i;
T.data[q].e = M.data[p].e;
++q;
}
}
return OK;
}