Java-算法-动态规划-背包问题
看完本篇文章可以再多练习相似题目
算法-动态规划-背包问题-附一
一. 背包问题介绍
1. 最原始的背包问题
给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。
2. 暴力解法
在最原始的背包问题中，我们假设每种物品只可以选一次，那么背包问题就可以转换为更为具体的0/1背包问题，即每种物品要与不要的问题。这种问题用暴力解法可以用回溯来做，即每种物品开始直接选择，然后递归，然后撤回对该物品的选择。
3. 引入动态规划
假设我们的物品的重量为w[i],物品的价值为v[i]，动态规划产生的dp表为dp[i][j]，其中i代表第i件物品，j代表此时背包的容量，那么我们需要求得的结果即为dp[i][j]代表此时来到第i件物品和背包容量为j的时候我们所能获得的最大价值。
二. 0/1背包
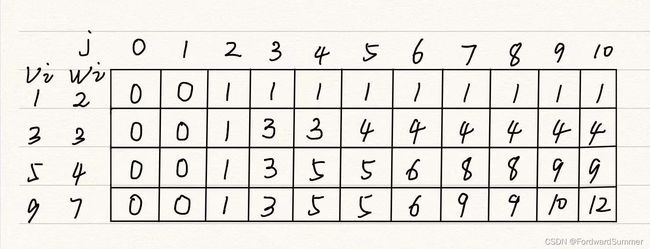
假设此时背包容量为10，物品为四个，我们的重量数组为w[i] = {2,3,4,7},对应的价值v[i] = {1,3,5,9}
1. dp表
dp表的行代表物品，列代表背包容量。在从j=0到j=10的过程中，我们逐渐从小到大一致满足我们的背包能放下的物品的最大值。
dp表的第一列很好确定，因为背包容量是0，所以都是0，dp表的第一行也好确定，就是当容量为j的时候能不能放下第一个物品。
而剩下的部分就要一个一个推得 。需要考虑能不能放下当前物品，能放下的话还需要和不要当前物品的情况比较。
2. 状态转移方程
观察上方的dp表，我们发现当前状态的值由上一层的状态确定。当前背包可能获得的最大价值由两部分决定，一是放当前物品，另外一个是不要当前物品，两者取最大值。
当前背包容量大于当前物品，那么最大值为
![dp[i][j] = Max(dp[i-1][j],dp[i-1][j-w[i]]+v[i])](http://img.e-com-net.com/image/info8/0565724f86634ac58a12415aa56e9012.gif){kind=small}
因为我们需要放此时的物品，所以对应的需要减去当前的重量，剩下的重量是上层背包的容积，而上层我们已经求出。
当前背包容量小于当前物品，那么最大值为上一层背包所能放下的最大价值
![dp[i][j] = dp[i-1][j]](http://img.e-com-net.com/image/info8/020a0f26f96e459e821003973f172a51.gif){kind=small}
3. 代码实现
class Solution {
public int maxValue(int N, int C, int[] v, int[] w) {
int[][] dp = new int[N][C+1];
// 第一件物品
for (int i = w[0]; i <= C; i++) {
dp[0][i] = v[0];
}
// 其余物品
for (int i = 1; i < N; i++) {
for (int j = 0; j <= C; j++) {
if(j < w[i]){
dp[i][j] = dp[i-1][j];
}
else{
dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);
}
}
}
return dp[N-1][C];
}
}4. 滚动数组
在获得状态转移方程时我们发现，当前层的值只与上一层有关，此时我们可以进行状态压缩，把n行的dp数组压缩成一行。即一维数组在不断变化，变化的过程就是二维数组中的每一行。不过要注意的是，因为在滚动的时候，我们需要用到dp[c-nums[i]]的信息，c是此时背包容量，nums[i]是当前物品的重量，这意味着从前往后压缩的时候，会覆盖掉此前的信息，但是回看滚动数组的使用方法，我们用的是上一层即上一次的结果，这意味着我们把这一层原来的信息进行了更新，会导致错误，所以一般我们进行状态压缩使用滚动数组的时候一般是从后往前压缩，这点尤其需要注意。
class Solution {
public int maxValue(int N, int C, int[] v, int[] w) {
int[]dp = new int[C+1];
for (int i = 0; i < N; i++) {
for (int j = C; j >= w[i]; j--) {
dp[j] = Math.max(dp[j],dp[j-w[i]]+v[i]);
}
}
return dp[C];
}
}压缩后的状态太庄毅方程：
![dp[j] = Max(dp[j],dp[j-w[i]]+v[i])](http://img.e-com-net.com/image/info8/0904972d0021446e94c923ef8f600b9e.gif){kind=small}
5. leetcode实战
（1）leetcode416分割等和子集
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。
输入：nums = [1,5,11,5] 输出：true 解释：数组可以分割成 [1, 5, 5] 和 [11]
输入：nums = [1,2,3,5] 输出：false 解释：数组不能分割成两个元素和相等的子集
解法一：二维数组
class Solution {
public boolean canPartition(int[] nums) {
int sum = 0;
int len = nums.length;
for(int i : nums) sum += i;
if(sum%2 != 0) return false;
int target = sum/2;
int[][] dp = new int[len+1][target+1];
for(int j = nums[0]; j <= target; j++){
dp[0][j] = nums[0];
}
for(int i = 1; i 解法一的状态压缩：一维数组（滚动数组）
class Solution {
public boolean canPartition(int[] nums) {
int sum = 0;
int len = nums.length;
for(int i : nums) sum += i;
if(sum%2 != 0) return false;
int target = sum/2;
int[] dp = new int[target+1];
for(int i = 0; i < len; i++){
for(int j = target; j >= 1; j--){
if(j >= nums[i]){
dp[j] = Math.max(dp[j],dp[j-nums[i]]+nums[i]);
}
}
}
return dp[target] == target;
}
}本题总结：
本题关键点在于求数组和，并把一半作为背包，把数组的值作为物品，且物品的重量和价值是相等的，数组里的值要或者不要，明显是0/1背包的问题。
（2）leetcode474一和零
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。请你找出并返回 strs 的最大子集的长度，该子集中 最多 有 m 个 0 和 n 个 1 。如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。
输入：strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出：4
解释：最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ，因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。
解法一：三维数组
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
int len = strs.length;
int[][] cnt = new int[len][2];
for(int i = 0; i < len; i++){
String temp = strs[i];
int num0 = 0;
int num1 = 0;
for(int j = 0; j < temp.length(); j++){
if(temp.charAt(j) == '0'){
num0++;
}
else{
num1++;
}
}
cnt[i][0] = num0;
cnt[i][1] = num1;
}
int[][][] dp = new int[len][m+1][n+1];
for(int i = 0; i <= m; i++){
for(int j = 0; j <= n; j++){
dp[0][i][j] = (cnt[0][0] <= i && cnt[0][1] <= j) ? 1 : 0;
}
}
for(int k = 1; k < len; k++){
for(int i = 0; i <= m; i++){
for(int j = 0; j <= n; j++){
int nochoose = dp[k-1][i][j];
int choose = (i>=cnt[k][0] && j >=cnt[k][1]) ? dp[k-1][i-cnt[k][0]][j-cnt[k][1]]+1 : 0;
dp[k][i][j] = Math.max(choose,nochoose);
}
}
}
return dp[len-1][m][n];
}
}解法一的状态压缩：二维数组
将三维数组的第一个维度当作行，后两个维度当作背包容量，那么三维数组可以压缩成两维度。注意，因为要用到第n个字符串0和1的数量，三重for循环的最外层的k层并不能省略掉。
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
int len = strs.length;
int[][] cnt = new int[len][2];
for(int i = 0; i < len; i++){
String temp = strs[i];
int num0 = 0;
int num1 = 0;
for(int j = 0; j < temp.length(); j++){
if(temp.charAt(j) == '0'){
num0++;
}
else{
num1++;
}
}
cnt[i][0] = num0;
cnt[i][1] = num1;
}
int[][] dp = new int[m+1][n+1];
for(int k = 0; k < len; k++){
for(int i = m; i >= cnt[k][0]; i--){
for(int j = n; j >= cnt[k][1]; j--){
dp[i][j] = Math.max(dp[i][j],dp[i-cnt[k][0]][j-cnt[k][1]]+1);
}
}
}
return dp[m][n];
}
}本题总结：
本题很容易产生误导，即认为这是一个多重背包的问题，其实仔细思考就会发现，我们的物品只有一个，就是该字符串要与不要的问题，背包还是那一个背包，不过把该背包分为了两个部分。
（3）leetcode494 目标和
给你一个整数数组 nums 和一个整数 target 。向数组中的每个整数前添加 '+' 或 '-' ，然后串联起所有整数，可以构造一个 表达式 ：例如，nums = [2, 1] ，可以在 2 之前添加 '+' ，在 1 之前添加 '-' ，然后串联起来得到表达式 "+2-1" 。返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
输入：nums = [1,1,1,1,1], target = 3
输出：5
解释：一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
解法一：三维数组
class Solution {
public int findTargetSumWays(int[] nums, int target) {
int sum = 0;
for(int i : nums) sum += i;
int len = nums.length;
int capacity = target > 0 ? sum-target : sum + target;
if(capacity < 0) return 0;
if(capacity % 2 != 0) return 0;
capacity /= 2;
int[][] dp = new int[len+1][capacity+1];
for(int i=0; i < len; i++){
dp[i][0] = 1;
}
for(int i = 1; i <= len; i++){
for(int j = 0; j <= capacity; j++){
if(j < nums[i-1]){
dp[i][j] = dp[i-1][j];
}
else{
dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i-1]];
}
}
}
return dp[len][capacity];
}
}解法一的状态压缩：一维数组
class Solution {
public int findTargetSumWays(int[] nums, int target) {
int sum = 0;
for(int i : nums) sum += i;
int len = nums.length;
int capacity = target > 0 ? sum-target : sum + target;
if(capacity < 0 ||capacity % 2 != 0) return 0;
capacity /= 2;
int[] dp = new int[capacity+1];
dp[0] = 1;
for(int i = 0; i < len; i++){
for(int j = capacity; j >= nums[i]; j--){
dp[j] = dp[j] + dp[j-nums[i]];
}
}
return dp[capacity];
}
}本题总结：
本题关键点在于分析出背包的容量，背包的容量和整体数组的和是相关的，但是target会出现正负的情况，要进行考虑。另外和传统0/1背包不同的是本题求的是一共可能的方法数，所以背包能放下的最大价值换成数量就可以了。这时会涉及到一个新的状态转移方程：
![dp[j] = dp[j] + dp[j-nums[i]];](http://img.e-com-net.com/image/info8/551d908f52964f609ab4008d62498a2c.gif){kind=small}
（4）leetcode1049 最后一块石头的重量
有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：
如果 x == y，那么两块石头都会被完全粉碎；
如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。
最后，最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下，就返回 0。
示例：
输入：stones = [2,7,4,1,8,1]
输出：1
解释：
组合 2 和 4，得到 2，所以数组转化为 [2,7,1,8,1]，
组合 7 和 8，得到 1，所以数组转化为 [2,1,1,1]，
组合 2 和 1，得到 1，所以数组转化为 [1,1,1]，
组合 1 和 1，得到 0，所以数组转化为 [1]，这就是最优值。
解法一：二维数组
class Solution {
public int lastStoneWeightII(int[] stones) {
int sum = 0;
for(int i : stones) sum += i;
int target = sum/2;
int len = stones.length;
int[][] dp = new int[len+1][target+1];
for(int j = stones[0]; j <= target; j++){
dp[0][j] = stones[0];
}
for(int i = 1; i < len; i++){
for(int j = 1; j <= target; j++){
if(j < stones[i]){
dp[i][j] = dp[i-1][j];
}
else{
dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-stones[i]]+stones[i]);
}
}
}
return Math.abs(sum - dp[len-1][target]-dp[len-1][target]);
}
}解法一的状态压缩：一维数组
class Solution {
public int lastStoneWeightII(int[] stones) {
int sum = 0;
for(int i : stones) sum += i;
int target = sum/2;
int len = stones.length;
int[] dp = new int[target+1];
for(int i = 0; i < len; i++){
for(int j = target; j >=stones[i]; j--){
dp[j] = Math.max(dp[j],dp[j-stones[i]]+stones[i]);
}
}
return Math.abs(sum - dp[target]-dp[target]);
}
}本题总结：
本题和494非常像，关键点在于能否转换为目标和的一半，在不超过数组总和的一般的情况下，我们选择的放入背包的物品让其都为负，另外一半都为正，两个部分相减即为结果。因为实际上石头是不可能为负的，因为我们总是拿大石头减去小石头，得到的结果还是正的，剩下的石头依然可以参与剩下的运算。
三.完全背包
1. 理论推导
完全背包的情况可以在0/1背包的问题上推导而来。核心点在于此时物品数量可以选择多个而不是0个或者1个。
那最朴素的思想是，在原来双重遍历的基础上，再加上一层对物品数量的遍历，即在最里层加上对物品数量的遍历，下限为0，上限为j/w[i]。
对应的代码为：
class Solution {
public int maxValue(int N, int C, int[] v, int[] w) {
int[]dp = new int[C+1];
for (int i = 0; i < N; i++) {
for (int j = C; j >= w[i]; j++) {
for(int k = 0; k <= j/w[i]; k--){
dp[j] = Math.max(dp[j],dp[j-k*w[i]]+k*v[i]);
}
}
}
return dp[C];
}
}2. 状态转移方程
因为对物品可以有多次选择，所以在选择物品时，我们的最大值不再只由上一层决定，而也与本层有关系，即：
那么相应的状态转移方程就为：
![dp[i][j] = Max(dp[i-1][j],dp[i][j-w[i]]+v[i])](http://img.e-com-net.com/image/info8/f49a4217bcf34064b8cd3abecde62fce.gif){kind=small}
我们可以发现完全背包和0/1背包最大区别就是在dp[i][j-w[i]]，意味着来到本层，我们还是可以取当前层的物品。
滚动数组压缩：
可以发现这和0/1背包的状态转移方程是一样的，但是要注意的是，0/1背包是逆序的，因为避免数据被覆盖，所以从后往前推。一个用的是旧数据，一个用到的是新数据，新数据里最大的区别就是可能已经多次选择了本层物品或者多次选择了上层物品。
3. 代码实现
class Solution {
public int maxValue(int N, int C, int[] v, int[] w) {
int[]dp = new int[C+1];
for (int i = 0; i < N; i++) {
for (int j = w[i]; j <= C; j++) {
dp[j] = Math.max(dp[j],dp[j-w[i]]+v[i]);
}
}
return dp[C];
}
}
4. leetcode实战
（1）leetcode518零钱兑换II
给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。
假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带符号整数。、
输入：amount = 5, coins = [1, 2, 5]
输出：4
解释：有四种方式可以凑成总金额：
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
class Solution {
public int change(int amount, int[] coins) {
int[] dp = new int[amount+1];
dp[0] = 1;
//状态转移方程
for(int i = 0; i < coins.length; i++){
for(int j = coins[i]; j <= amount; j++){
dp[j] += dp[j-coins[i]];
}
}
return dp[amount];
}
}本题总结：
本题的背包容量很容易得是amount，完全背包要涉及到本层，且此题求的是方法数，和0/1背包问题中leetcode494 目标和 的状态转移方程是一样的，即
完全背包，背包容量遍历从小往大，不需要像0/1背包从大往小，因为我们需要的就是已经更改后的数据。
（2）leetcode279完全平方数
给你一个整数 n ，返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。
输入：n = 12 输出：3 解释：12 = 4 + 4 + 4
输入：n = 13 输出：2 解释：13 = 4 + 9
class Solution {
public int numSquares(int n) {
int[] dp = new int[n+1];
for(int i = 1; i <=n; i++){
dp[i] = i;//每次最坏结果就是1+1+1+...+1
for(int j = 1; j*j <= i ; j++){
dp[i] = Math.min(dp[i],dp[i-j*j]+1);
}
}
return dp[n];
}
}本题总结：
n即是target，物品数量不限，无限背包，物品可以预先处理，每次物品耗费一个坑位，求最小值，本体最巧妙的地方在于可以预设最大值为档次循环的背包容量，即1+...+1的情况。
（3）leetcode322 零钱兑换
给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。你可以认为每种硬币的数量是无限的。
输入：coins = [1, 2, 5], amount = 11 输出：3 解释：11 = 5 + 5 + 1
class Solution {
public int coinChange(int[] coins, int amount) {
int[] dp = new int[amount+1];
dp[0] = 0;
for(int i = 1; i <= amount; i++){
dp[i] = Integer.MAX_VALUE;
}
for(int i = 0; i < coins.length; i++){
for(int j = coins[i]; j <= amount; j++){
if(dp[j-coins[i]] != Integer.MAX_VALUE){
dp[j] = Math.min(dp[j],dp[j-coins[i]]+1);
}
}
}
return dp[amount] != Integer.MAX_VALUE ? dp[amount]:-1;
}
}class Solution {
public int coinChange(int[] coins, int amount) {
int[] dp = new int[amount+1];
dp[0] = 0;
for(int i = 1; i <= amount; i++){
dp[i] = 0x3f3f3f3f;//利用0x3f3f3f3f可以避免溢出
}
for(int i = 0; i < coins.length; i++){
for(int j = coins[i]; j <= amount; j++){
dp[j] = Math.min(dp[j],dp[j-coins[i]]+1);
}
}
return dp[amount] != 0x3f3f3f3f ? dp[amount]:-1;
}
}本题总结：
本题target是背包容量，物品是硬币，每个硬币可以取多次，求最小值，要初始化dp数组用最大值覆盖，值得注意的是最大值+1可能溢出变成负数，会对结果造成干扰，所以可以用0x3f3f3f3f代替【1】。
（4）leetcode377 排列总和
给你一个由 不同 整数组成的数组 nums ，和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。
输入：nums = [1,2,3], target = 4
输出：7
解释：
所有可能的组合为：
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意，顺序不同的序列被视作不同的组合。
class Solution {
public int combinationSum4(int[] nums, int target) {
int[] dp = new int[target+1];
dp[0] = 1;
for(int j = 0; j <= target; j++){
for(int i = 0; i < nums.length; i++){
if(j >= nums[i]) dp[j] += dp[j-nums[i]];
}
}
return dp[target];
}
}
本题总结：
本题target是背包容量，物品是nums[i]，每个物品可以取多次，求组合数。
如果求组合数就是外层for循环遍历物品，内层for遍历背包。
如果求排列数就是外层for遍历背包，内层for循环遍历物品。【2】
如果物品放在外面可能会漏掉{2，1}这种组合，对{1，2}是没影响的。
（5）leetcode139 单词拆分
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。注意：不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。
输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以由 "leet" 和 "code" 拼接成。
class Solution {
public boolean wordBreak(String s, List wordDict) {
boolean[] dp = new boolean[s.length()+1];
dp[0] = true;
for(int i = 1; i <= s.length(); i++){
for(int j = 0; j < i; j++){
if(dp[j] && wordDict.contains(s.substring(j,i))){
dp[i] = true;
}
}
}
return dp[s.length()];
}
} 本题总结：
本题的背包就是s字符串，物品就是wordDict，那么物品可以多次使用，完全背包，双重遍历，把字符串逐一切割，判断该子字符串是否在wordDict里，dp[j]为之前已经判断过的部分，可以直接判断。
四. 多重背包
0/1背包是拿与不拿的问题，完全背包是每件可以无限拿的问题，而多重背包是每件物品可以拿的数量是有限的问题。
从0/1背包的基础上，只需要再满足额外的条件即可，一是对于物品数量的限制，二是物品一定数量之下对背包容量的限制。即
![dp[j] = Max(dp[j],dp[j-k*w[i]]+k*v[i])](http://img.e-com-net.com/image/info8/94b0016ffd9e4918a56196c4d5d393ba.gif){kind=small}
并且约束为
![j >= k*w[i]](http://img.e-com-net.com/image/info8/8f567393e3474f70866f3a7274c1af55.gif){kind=small}
, ![k <= n[i]](http://img.e-com-net.com/image/info8/28030bac45894dd8b64e6dbc1bca6a7d.gif){kind=small}
class Solution {
public int maxValue(int N, int C, int[] n, int[] v, int[] w) {
int[] dp = new int[C + 1];
for (int i = 0; i < N; i++) {
for (int j = C; j >= w[i]; j--) {
for (int k = 0; k <= n[i] && j >= k * w[i]; k++) {
dp[j] = Math.max(dp[j], dp[j - k * w[i]] + k * v[i]);
}
}
}
return dp[C];
}
}参考来源：
【1】leetcode 宫水三叶 背包问题
【2】b站 代码随想录 卡尔
【3】b站 睿爸信奥 听懂不翻车系列之--背包问题