2021年第十二届蓝桥杯省赛Java B组真题及详细题解
A试题 : ASC【填空题】
本题总分: 5 分
【1、问题描述】
已知大写字母 A 的 ASCII 码为 65,请问大写字母 L 的 ASCII 码是多少?
【2、答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
【3、解题思路】
ASCII 码,其中大写字母 A 的 ASCII 码为 65。由于 L 在字母表中在 A 的后面,因此它的 ASCII 码应该比 A 的 ASCII 码大。根据字母表的顺序,L 的 ASCII 码应该为 65 + 11 = 76。因此,大写字母 L 的 ASCII 码为 76。
【4、答案】
76
B试题 : 卡片【填空题】
本题总分: 5 分
【1、问题描述】
小蓝有很多数字卡片,每张卡片上都是数字 0 到 9。 小蓝准备用这些卡片来拼一些数,他想从 1 开始拼出正整数,每拼一个, 就保存起来,卡片就不能用来拼其它数了。 小蓝想知道自己能从 1 拼到多少。 例如,当小蓝有 30张卡片,其中 0 到 9 各 3 张,则小蓝可以拼出 1 到 10, 但是拼 11 时卡片 1 已经只有一张了,不够拼出 11。 现在小蓝手里有 0到 9的卡片各 2021 张,共 20210 张,请问小蓝可以从 1拼到多少?
提示:建议使用计算机编程解决问题
【2、答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
【3、解题思路】
这道题可以使用贪心算法来解决。
首先,我们需要将每个数字的卡片数量按照从大到小的顺序排序。这样,我们在拼数字时,就可以尽可能地使用卡片数量更多的数字卡片来拼出当前数字。
然后,我们从数字 1 开始,依次尝试拼出每个数字。对于每个数字,我们将它转换成字符串,然后遍历字符串中的每个字符。对于每个字符,我们检查对应数字的卡片数量是否大于 0。如果大于 0,则将对应卡片数量减 1,并继续检查下一个字符。如果小于等于 0,则说明无法拼出当前数字,我们就停止往后拼数字,因为后面的数字肯定更大,需要的卡片数量也更多。
当我们无法拼出当前数字时,我们就可以退出循环,输出最大能拼出的数字。
【4、代码题解】
public class Main {
public static void main(String[] args) {
int[] cards = new int[10];
Arrays.fill(cards, 2021); // 初始化每张卡片的数量为 2021
int num = 1; // 从 1 开始拼数
while (true) {
String s = Integer.toString(num); // 将数字转换为字符串
boolean flag = true; // 标记能否拼出当前数字
for (char c : s.toCharArray()) {
int digit = c - '0'; // 获取当前数字
if (cards[digit] == 0) { // 如果当前数字的卡片数量为 0,则无法拼出当前数字
flag = false;
break;
}
cards[digit]--; // 拼出当前数字后,将对应卡片数量减 1
}
if (flag) { // 如果能够拼出当前数字,则尝试拼下一个数字
num++;
} else { // 如果无法拼出当前数字,则退出循环
break;
}
}
System.out.println(num-1); // 输出最大能拼出的数字
}
}
【5、答案】
3181
C试题 : 直线【填空题】
本题总分: 10 分
【1、问题描述】
在平面直角坐标系中,两点可以确定一条直线。如果有多点在一条直线上,
那么这些点中任意两点确定的直线是同一条。
给定平面上 2 × 3 个整点 {(x,y)|0 ≤ x < 2,0 ≤ y < 3, x ∈ Z,y ∈ Z},即横坐标
是 0 到 1 (包含 0 和 1) 之间的整数、纵坐标是 0 到 2 (包含 0 和 2) 之间的整数
的点。这些点一共确定了 11 条不同的直线。
给定平面上 20 × 21 个整点 {(x,y)|0 ≤ x < 20,0 ≤ y < 21, x ∈ Z,y ∈ Z},即横
坐标是 0 到 19 (包含 0 和 19) 之间的整数、纵坐标是 0 到 20 (包含 0 和 20) 之
间的整数的点。请问这些点一共确定了多少条不同的直线。
【2、答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
【3、解题思路】
以上解题思路是枚举所有点对,计算它们之间的斜率,最后将斜率相同的直线视为同一条直线。
具体的解题思路如下:
- 枚举所有点对
首先,我们需要枚举所有的点对,即平面上所有不同的点对。这里可以使用两个 for 循环来实现:
然后将平面上所有的点添加到一个 Set 集合中。
- 计算斜率
接下来,我们需要计算点对之间的斜率。对于两个点 ( x 1 , y 1 ) (x_1, y_1) (x1,y1) 和 ( x 2 , y 2 ) (x_2, y_2) (x2,y2),它们之间的斜率为 y 2 − y 1 x 2 − x 1 \frac{y_2 - y_1}{x_2 - x_1} x2−x1y2−y1。但是,如果 x 1 = x 2 x_1 = x_2 x1=x2,则斜率不存在。因此,我们需要对这种情况进行特判。
对于每个点对,我们可以使用一个双重循环来计算它们之间的斜率
- 去重
最后,我们需要对斜率相同的直线进行去重。这里我们可以使用一个 Set 集合来存储所有不同的直线。
最终,我们只需要输出 Set 集合的大小,即为不同直线的数量。
完整代码如下:
【4、代码题解】
import java.util.*;
public class Main {
public static void main(String[] args) {
Set<List<Integer>> points = new HashSet<>(); // 平面上的点集
for (int i = 0; i < 20; i++) {
for (int j = 0; j < 21; j++) {
points.add(Arrays.asList(i, j)); // 添加平面上的点
}
}
Set<List<Integer>> lines = new HashSet<>(); // 直线的集合
for (List<Integer> p1 : points) {
for (List<Integer> p2 : points) {
if (p1.equals(p2)) continue; // 如果两个点相同,则跳过
int dx = p2.get(0) - p1.get(0); // 计算斜率的分子
int dy = p2.get(1) - p1.get(1); // 计算斜率的分母
int gcd = gcd(dx, dy); // 计算分子和分母的最大公约数
List<Integer> line = Arrays.asList(dx / gcd, dy / gcd); // 表示直线的斜率
lines.add(line); // 将直线添加到集合中
}
}
System.out.println(lines.size()); // 输出不同直线的数量
}
// 计算两个数的最大公约数
private static int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
}
【5、答案】
40257
D试题 : 货物摆放【填空题】
本题总分: 10 分
【1、问题描述】
现在,小蓝有 n箱货物要摆放在仓库,每箱货物都是规则的正方体。小蓝规定了长、宽、高三个互相垂直的方向,每箱货物的边都必须严格平行于长、宽、高。
小蓝希望所有的货物最终摆成一个大的长方体。即在长、宽、高的方向上分别堆 L、W、H 的货物,满足n=L×W×H。
给定 n,请问有多少种堆放货物的方案满足要求。
例如,当 n = 4 时,有以下 6 种方案:1×1×4、1×2×2、1×4×1、2×1×2、2 × 2 × 1、4 × 1 × 1。
请问,当 n = 2021041820210418(注意有 16位数字)时,总共有多少种方案?
提示:建议使用计算机编程解决问题。
【2、答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
【3、解题思路】
这个问题是一个经典的组合数学问题,可以用数学公式解决。以下是解题思路:
首先,将 n n n 分解成 L × W × H L \times W \times H L×W×H 的形式,其中 L L L、 W W W、 H H H 分别表示长、宽、高。
由于长、宽、高互相垂直,因此可以假设 L ≥ W ≥ H L \geq W \geq H L≥W≥H,从而减少重复计算。
枚举 L L L、 W W W、 H H H,计算满足条件的方案数。具体来说,可以枚举 L L L 和 W W W,然后计算 H H H。如果 L × W × H L \times W \times H L×W×H 等于 n n n,则说明这个方案满足条件。
对于每个满足条件的方案,计算组合数。具体来说,可以先将 L L L、 W W W、 H H H 排序,然后将它们插入到一个长度为 L + W + H − 3 L+W+H-3 L+W+H−3 的数组中,其中 L − 1 L-1 L−1 个位置插入 L L L, W − 1 W-1 W−1 个位置插入 W W W, H − 1 H-1 H−1 个位置插入 H H H。这样,就得到了一个长度为 L + W + H − 3 L+W+H-3 L+W+H−3 的排列,从中选择 L − 1 L-1 L−1 个位置插入 L L L, W − 1 W-1 W−1 个位置插入 W W W,就得到了一个长度为 L + W + H − 3 L+W+H-3 L+W+H−3 的组合,即 C L + W + H − 3 L − 1 × C W + H − 2 W − 1 C_{L+W+H-3}^{L-1} \times C_{W+H-2}^{W-1} CL+W+H−3L−1×CW+H−2W−1。
对于每个满足条件的方案,累加组合数,最后得到的结果就是方案数。
总的来说,这个问题的难点在于如何计算组合数。如果使用组合数学的知识,可以得到一个简单而有效的计算方法。
【4、代码题解】
import java.math.BigInteger;
public class Main {
public static void main(String[] args) {
BigInteger n = new BigInteger("2021041820210418");
// 计算立方体根号
BigInteger root = root(n, 3);
BigInteger cnt = BigInteger.ZERO; // 方案数
// 枚举长、宽、高
for (BigInteger l = BigInteger.ONE; l.compareTo(root) <= 0; l = l.add(BigInteger.ONE)) {
for (BigInteger w = l; w.multiply(l).compareTo(n) <= 0; w = w.add(BigInteger.ONE)) {
BigInteger h = n.divide(l.multiply(w)); // 计算高
if (l.multiply(w).multiply(h).equals(n)) { // 验证是否满足条件
BigInteger c = C(l.add(w).add(h).subtract(BigInteger.valueOf(3)), l.subtract(BigInteger.ONE))
.multiply(C(w.add(h).subtract(BigInteger.valueOf(2)), w.subtract(BigInteger.ONE))); // 计算组合数
cnt = cnt.add(c); // 累加方案数
}
}
}
System.out.println(cnt);
}
// 计算组合数
public static BigInteger C(BigInteger n, BigInteger m) {
BigInteger res = BigInteger.ONE;
for (BigInteger i = BigInteger.ZERO; i.compareTo(m) < 0; i = i.add(BigInteger.ONE)) {
res = res.multiply(n.subtract(i)).divide(i.add(BigInteger.ONE));
}
return res;
}
// 计算整数的 k 次方根,采用二分法
public static BigInteger root(BigInteger n, int k) {
BigInteger lo = BigInteger.ZERO, hi = n;
while (lo.compareTo(hi) < 0) {
BigInteger mid = lo.add(hi).add(BigInteger.ONE).divide(BigInteger.valueOf(2));
if (mid.pow(k).compareTo(n) > 0) {
hi = mid.subtract(BigInteger.ONE);
} else {
lo = mid;
}
}
return lo;
}
}
【5、答案】
2430
E试题 : 路径【填空题】
本题总分: 15 分
【1、问题描述】
小蓝学习了最短路径之后特别高兴,他定义了一个特别的图,希望找到图 中的最短路径。
小蓝的图由 2021 个结点组成,依次编号 1 至 2021。
对于两个不同的结点 a, b,如果 a 和 b 的差的绝对值大于 21,则两个结点 之间没有边相连;如果 a 和 b 的差的绝对值小于等于 21,则两个点之间有一条 长度为 a 和 b 的最小公倍数的无向边相连。
例如:结点 1 和结点 23 之间没有边相连;结点 3 和结点 24 之间有一条无 向边,长度为 24;结点 15 和结点 25 之间有一条无向边,长度为 75。
请计算,结点 1 和结点 2021 之间的最短路径长度是多少。
提示:建议使用计算机编程解决问题。
【2、答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
【3、解题思路】
题目要求计算结点 1 和结点 2021 之间的最短路径长度,可以使用 Dijkstra 算法求解。
首先需要初始化结点之间的距离,对于两个结点 i 和 j,如果它们的差的绝对值大于 21,则它们之间没有边相连;否则,它们之间有一条长度为它们的最小公倍数的无向边相连。
在 Dijkstra 算法中,需要维护一个集合 S,表示已经找到最短路径的结点集合,以及一个数组 d,表示每个结点到起点的最短距离。初始时,集合 S 中只包含起点,数组 d 中只有起点的距离为 0,其它结点的距离为无穷大。
每次从未加入集合 S 的结点中选择距离起点最近的结点 u,将其加入集合 S,并更新与结点 u 相连的结点 v 的距离,即:
d[v] = min(d[v], d[u] + w(u, v))
其中 w(u, v) 表示结点 u 和结点 v 之间的距离。在本题中,w(u, v) 等于结点 u 和结点 v 的最小公倍数。
重复上述过程,直到结点 2021 加入集合 S,此时数组 d 中的值即为结点 1 到结点 2021 的最短路径长度。
由于本题中结点的数量较小,因此可以直接使用 HashMap 存储结点之间的距离,而不需要使用邻接矩阵或邻接表等数据结构。
【4、代码题解】
import java.util.*;
public class Main {
static final int N = 2021;
static final int INF = 0x3f3f3f3f;
static int[] d = new int[N]; // 存储结点到起点的距离
static boolean[] vis = new boolean[N]; // 标记结点是否已经加入集合 S
static Map<Integer, Map<Integer, Integer>> g = new HashMap<>(); // 存储结点之间的距离
// 求两个数的最大公约数
static int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
// 求两个数的最小公倍数
static int lcm(int a, int b) {
return a * b / gcd(a, b);
}
// Dijkstra 算法求解最短路径
static void dijkstra() {
// 使用 PriorityQueue 来维护未加入集合 S 的结点中距离起点最近的结点
PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[1]));
pq.offer(new int[]{1, 0}); // 起点到起点的距离为 0
d[1] = 0;
while (!pq.isEmpty()) {
int[] curr = pq.poll();
int u = curr[0], dist = curr[1];
if (vis[u]) continue;
vis[u] = true;
if (u == N - 1) break; // 已经到达终点
// 枚举与结点 u 相连的结点
Map<Integer, Integer> neighbors = g.getOrDefault(u, new HashMap<>());
for (int v : neighbors.keySet()) {
int w = neighbors.get(v);
if (vis[v]) continue;
int newDist = dist + w;
if (newDist < d[v]) {
d[v] = newDist;
pq.offer(new int[]{v, newDist});
}
}
}
}
public static void main(String[] args) {
// 初始化结点之间的距离
for (int i = 1; i <= N; i++) {
Map<Integer, Integer> neighbors = new HashMap<>();
for (int j = i + 1; j <= N; j++) {
if (Math.abs(i - j) > 21) continue;
int w = lcm(i, j);
neighbors.put(j, w);
}
g.put(i, neighbors);
}
Arrays.fill(d, INF); // 初始化距离为无穷大
dijkstra(); // 求解最短路径
System.out.println(d[N - 1]); // 输出结点 1 到结点 2021 的最短路径长度
}
}
【5、答案】
10266837
F试题 : 时间显示 【编程题】
时间限制: 1.0s 内存限制: 512.0MB 本题总分: 15 分
【问题描述】
小蓝要和朋友合作开发一个时间显示的网站。
在服务器上,朋友已经获取了当前的时间,用一个整数表示,值为从 19701970 年 11 月 11 日 00:00:0000:00:00 到当前时刻经过的毫秒数。
现在,小蓝要在客户端显示出这个时间。小蓝不用显示出年月日,只需要显示出时分秒即可,毫秒也不用显示,直接舍去即可。
给定一个用整数表示的时间,请将这个时间对应的时分秒输出。
【输入格式】:
输入一行包含一个整数,表示时间。
【输出格式】:`
输出时分秒表示的当前时间,格式形如
HH:MM:SS,其中HH表示时,值为 00 到 2323,MM表示分,值为 00 到 5959,SS表示秒,值为 00 到 5959。时、分、秒 不足两位时补前导 00。
【样例输入1】 :
46800999
【样例输出1】 :
13:00:00
【样例输入2】 :
1618708103123
【样例输出2】 :
01:08:23
【评测用例规模与约定】:
对于所有评测用例,给定的时间为不超过 10的18次方的正整数。
运行限制
- 最大运行时间:1s
- 最大运行内存: 512M
【解题思路】
代码思路:
首先读入时间,题目中给定的时间是UTC时间,单位为毫秒。
根据题意,我们需要计算出当前时间对应的小时、分钟和秒数。我们可以先计算出总共经过的小时数,即
time / 3600000,然后用余数计算出分钟数,即(time % 3600000) / 60000,最后用余数计算出秒数,即(time % 60000) / 1000。输出结果,注意时、分、秒不足两位时需要在前面补上 0。
时间复杂度: O ( 1 ) O(1) O(1)。
【代码题解】
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// 读入时间,单位为毫秒
int time = sc.nextInt();
// 计算小时、分钟和秒数
int hour = time / 3600000 % 24; // 对24取模,得到小时数
int minute = (time % 3600000) / 60000; // 取余数,得到分钟数,再除以60得到分钟数
int second = (time % 60000) / 1000; // 取余数,得到秒数,再除以1000得到秒数
// 输出结果,注意时、分、秒不足两位时需要在前面补上 0
System.out.printf("%02d:%02d:%02d", hour, minute, second);
}
}
G试题 : 最少砝码【编程题】
时间限制: 1.0s 内存限制: 512.0MB 本题总分: 20 分
【问题描述】
你有一架天平。现在你要设计一套砝码,使得利用这些砝码可以称出任意 小于等于 N的正整数重量。
那么这套砝码最少需要包含多少个砝码?
注意砝码可以放在天平两边。
【输入格式】:
输入包含一个正整数 N。
【输出格式】:`
输出一个整数代表答案。
【样例输入】 :
7
【样例输出】 :
3
【评测用例规模与约定】:
对于所有评测用例,1 ≤ N ≤ 1000000000。
【样例说明】
33 个砝码重量是 1、4、6,可以称出 1 至 7的所有重量。
1 = 1;
2 = 6 − 4(天平一边放 66,另一边放 44);
3 = 4 − 1;
4 = 4;
5 = 6 − 1;
6 = 6;
7 = 1 + 6;
少于 3 个砝码不可能称出 1 至 7 的所有重量。
【解题思路】
算法思路
本题是一道贪心算法的经典题目。我们需要设计一套砝码,使得利用这些砝码可以称出任意小于等于N的正整数重量,且砝码最少。
首先,我们考虑最小的砝码,显然是1,因为1可以表示任意小于等于1的正整数。接下来,我们考虑如何设计更多的砝码。我们发现,如果我们有了一个砝码w,那么我们可以通过以下两种方式得到更多的砝码:
- 在w的基础上增加一个和w相等的砝码;
- 在w的基础上增加一个和w之和相等的砝码。
例如,如果我们已经有了一个砝码6,那么我们可以通过以下两种方式得到更多的砝码:
- 增加一个砝码6,这样我们就有了两个6的砝码,可以表示任意小于等于12的正整数;
- 增加一个砝码10,这样我们就有了6和10两个砝码,可以表示任意小于等于16的正整数。
因此,我们可以从小到大枚举每个正整数,对于每个正整数i,我们都尝试用已有的砝码表示出来。如果无法表示,则需要添加一个新的砝码,这个砝码的重量就是i减去已有砝码可以表示的最大重量。
具体来说,我们可以维护一个变量max_weight,表示当前已有砝码可以表示的最大重量。对于每个正整数i,如果i可以用已有砝码表示出来,则什么也不做;如果无法表示,则需要添加一个新的砝码,这个砝码的重量就是i减去max_weight。
最后,我们需要注意一下特殊情况,即N=1时,答案为1。
【代码题解】
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
if (n == 1) { // 特判:当n=1时,答案为1
System.out.println(1);
} else {
int ans = 1; // 记录砝码的数量,初始值为1,因为最小的砝码是1
int max_weight = 1; // 记录当前已有砝码可以表示的最大重量,初始值为1
while (max_weight < n) { // 当已有砝码可以表示的最大重量小于n时,继续添加砝码
ans++; // 砝码数量加1
max_weight = 2 * max_weight + 1; // 新砝码的重量是已有砝码可以表示的最大重量加1
}
System.out.println(ans); // 输出答案
}
}
}
H试题 : 杨辉三角形【编程题】
时间限制: 1.0s 内存限制: 512.0MB 本题总分: 20 分
【问题描述】
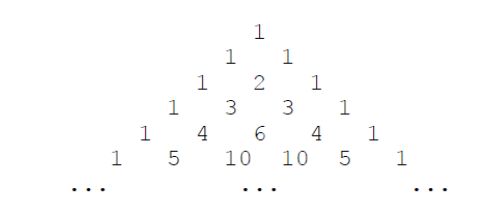
下面的图形是著名的杨辉三角形:
如果我们按从上到下、从左到右的顺序把所有数排成一列,可以得到如下数列: 1,1,1,1,2,1,1,3,3,1,1,4,6,4,1,⋯1,1,1,1,2,1,1,3,3,1,1,4,6,4,1,⋯
给定一个正整数 N,请你输出数列中第一次出现 N是在第几个数?
输入描述
输入一个整数 N。
输出描述
输出一个整数代表答案。
输入输出样例
示例 1
输入
6
输出
13
评测用例规模与约定
对于 2020 的评测用例,1≤N≤10; 对于所有评测用例,1≤N≤1000000000
运行限制
- 最大运行时间:1s
- 最大运行内存: 256M
【解题思路】
题目要求我们输出数列中第一次出现 N 的位置,其中数列是杨辉三角形按从上到下、从左到右的顺序排列的。因此,我们可以先构建杨辉三角形,然后遍历这个数组,找到第一次出现 N 的位置。
构建杨辉三角形的方法是,从第二行开始,每一行的第一个数和最后一个数都是 1,中间的数等于上一行对应位置的数和上一行对应位置前一个数的和。我们可以用一个二维数组来存储杨辉三角形。
遍历数组时,我们可以用一个计数器记录当前的位置,遇到第一次出现 N 的数时,输出计数器的值即可。
时间复杂度: O ( N 2 ) O(N^2) O(N2)
空间复杂度: O ( N 2 ) O(N^2) O(N2)
【代码题解】
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
// 构建杨辉三角形
int[][] triangle = new int[n][n];
for (int i = 0; i < n; i++) {
triangle[i][0] = 1; // 每一行的第一个数都是1
triangle[i][i] = 1; // 每一行的最后一个数都是1
for (int j = 1; j < i; j++) {
triangle[i][j] = triangle[i-1][j-1] + triangle[i-1][j]; // 中间的数等于上一行对应位置的数和上一行对应位置前一个数的和
}
}
// 遍历数组找到第一次出现N的位置
int count = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j <= i; j++) {
count++;
if (triangle[i][j] == n) {
System.out.println(count);
return;
}
}
}
}
}
I试题 : 双向排序【编程题】
https://www.lanqiao.cn/problems/1458/learning/
J试题 :括号序列 【编程题】
时间限制: 1.0s 内存限制: 512.0MB 本题总分: 25 分
【问题描述】
给定一个括号序列,要求尽可能少地添加若干括号使得括号序列变得合法,当添加完成后,会产生不同的添加结果,请问有多少种本质不同的添加结果。
两个结果是本质不同的是指存在某个位置一个结果是左括号,而另一个是右括号。
例如,对于括号序列 ((()(((),只需要添加两个括号就能让其合法,有以下几种不同的添加结果:()()()()()()、()(())()(())、(())()(())()、(()())(()()) 和 ((()))((()))。
【输入格式】:
输入一行包含一个字符串 s,表示给定的括号序列,序列中只有左括号和右括号。
【输出格式】:`
输出一个整数表示答案,答案可能很大,请输出答案除以 10000000071000000007 (即 109+7)109+7) 的余数。
【样例输入】 :
((()
【样例输出】 :
5
【评测用例规模与约定】:
对于 4040 的评测用例,∣s∣≤200。
对于所有评测用例,1≤∣s∣≤5000。
【解题思路】
本题是一个动态规划问题。
目标是添加最少的括号使得序列合法,显然,添加的括号数量越少,其本质不同的情况就会越少。
因此,考虑定义状态: f [ i ] [ j ] f[i][j] f[i][j] 表示将区间 [ i , j ] [i,j] [i,j] 变为合法括号序列所添加的最少括号数。
接下来,考虑状态转移方程:
- 当 s [ i ] = ′ ( ′ s[i]='(' s[i]=′(′ 且 s [ j ] = ′ ) ′ s[j]=')' s[j]=′)′ 时, f [ i ] [ j ] = f [ i + 1 ] [ j − 1 ] f[i][j]=f[i+1][j-1] f[i][j]=f[i+1][j−1];
- 当 s [ i ] = ′ ( ′ s[i]='(' s[i]=′(′ 且 s [ j ] = ′ ( ′ s[j]='(' s[j]=′(′ 时,可以在 j j j 位置添加一个 ‘)’,则 f [ i ] [ j ] = f [ i ] [ j − 1 ] + 1 f[i][j]=f[i][j-1]+1 f[i][j]=f[i][j−1]+1;
- 当 s [ i ] = ′ ) ′ s[i]=')' s[i]=′)′ 且 s [ j ] = ′ ) ′ s[j]=')' s[j]=′)′ 时,可以在 i i i 位置添加一个 ‘(’,则 f [ i ] [ j ] = f [ i + 1 ] [ j ] + 1 f[i][j]=f[i+1][j]+1 f[i][j]=f[i+1][j]+1;
- 当 s [ i ] = ′ ) ′ s[i]=')' s[i]=′)′ 且 s [ j ] = ′ ( ′ s[j]='(' s[j]=′(′ 时,可以在 j j j 位置添加一个 ‘)’,也可以在 i i i 位置添加一个 ‘(’,取两种情况的较小值,即 f [ i ] [ j ] = min ( f [ i + 1 ] [ j ] + 1 , f [ i ] [ j − 1 ] + 1 ) f[i][j]=\min(f[i+1][j]+1,f[i][j-1]+1) f[i][j]=min(f[i+1][j]+1,f[i][j−1]+1)。
考虑边界情况,当 i = j i=j i=j 时, f [ i ] [ j ] = 1 f[i][j]=1 f[i][j]=1。
最后,答案为 f [ 1 ] [ n ] f[1][n] f[1][n]。
时间复杂度: O ( n 2 ) O(n^2) O(n2)。
【代码题解】
import java.util.Scanner;
public class Main {
static final int MOD = 1000000007;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String s = sc.nextLine().trim(); // 读入字符串
int n = s.length(); // 字符串长度
int[][] f = new int[n+1][n+1]; // 定义状态数组 f
for (int i = 1; i <= n; i++) {
f[i][i] = 1; // 初始化状态,当区间长度为 1 时,不需要添加括号
}
for (int len = 2; len <= n; len++) { // 枚举区间长度
for (int i = 1; i <= n-len+1; i++) { // 枚举区间左端点
int j = i + len - 1; // 区间右端点
if (s.charAt(i-1) == '(' && s.charAt(j-1) == ')') { // 情况1:s[i]='(',s[j]=')'
f[i][j] = f[i+1][j-1]; // 不需要添加括号
} else {
f[i][j] = Math.min(f[i+1][j], f[i][j-1]) + 1; // 情况2和情况3:添加括号
if (s.charAt(i-1) == '(' && s.charAt(j-1) == '(') { // 情况2:s[i]='(',s[j]='('
f[i][j] = Math.min(f[i][j], f[i][j-1]+1); // 在 j 位置添加一个 ')'
} else if (s.charAt(i-1) == ')' && s.charAt(j-1) == ')') { // 情况3:s[i]=')',s[j]=')'
f[i][j] = Math.min(f[i][j], f[i+1][j]+1); // 在 i 位置添加一个 '('
}
}
}
}
System.out.println(f[1][n] % MOD); // 输出答案
}
}