超强二叉树解析(数组,链表实现,8种遍历方法,前,中,后序线索化二叉树及其遍历)---风之java

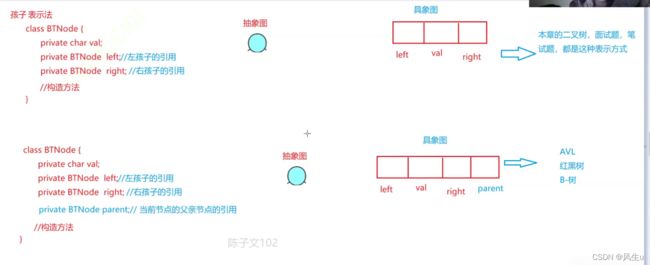
链表实现

先创建一个节点类

public class TreeNode {
    int value;//数据
    TreeNode left;//指向左子树
    TreeNode right;//指向右子树
    public TreeNode(){}
    public TreeNode(int value){
        this.value=value;
        left=null;
        right=null;
    }
}

利用数组建立二叉树

利用递归一一将数组中的数全部存储到二叉树中建立二叉树

   public TreeNode create(char[] arr,int index){
        if(index>=arr.length){
            return null;
        }else{
            TreeNode tmpNode=new TreeNode((int)(arr[index]));
            tmpNode.left=create(arr,2*index);
            tmpNode.right=create(arr,2*index+1);
            return tmpNode;
        }
    }

整体代码实现

```java
public class BinaryTree {
    public TreeNode root;
    public TreeNode(){}
    public BinaryTree(char[] ch,int index){
        root=create(ch,index);
    }
    //将数组表示法转换为链表表示法
    public TreeNode create(char[] arr,int index){
        if(index>=arr.length){
            return null;
        }else{
            TreeNode tmpNode=new TreeNode((int)(arr[index]));
            tmpNode.left=create(arr,2*index);
            tmpNode.right=create(arr,2*index+1);
            return tmpNode;
        }
    }

直接添加元素，建立二叉排序树

    public void add(int data){
        TreeNode newNode=new TreeNode(data);
        //建立树根
        if(root==null){
            root=newNode;
            return;
        }
        TreeNode cur=root;
        while(true){
            if(newNode.value<cur.value){
                if(cur.left==null){
                    cur.left=newNode;
                    return;
                }else{
                    cur=cur.left;
                }
            }else{
                if(cur.right==null){
                    cur.right=newNode;
                    return;
                }else{
                    cur=cur.right;
                }
            }
        }
    }

二叉树的搜索

可以看到二叉树的搜索是建立在二叉排序树的基础上

    //查找该二叉树上是否含有该元素
    public boolean findTreeNode(TreeNode root,int value){
        if(root==null){
            return false;
        }else{
            if(root.value==value){
                return true;
            }else{
                if(value<root.value){
                    count++;
                    return findTreeNode(root.left,value);
                }else{
                    count++;
                    return findTreeNode(root.right,value);
                }
            }
        }
    }

二叉运算树

先创建一个节点类

public class TreeNode {
    int value;
    TreeNode left;
    TreeNode right;
    public TreeNode(){}
    public TreeNode(int data){
        this.value=data;
        left=null;
        right=null;
    }
}

接下来实现二叉运算树

public class BinaryTree {
    public TreeNode root;
    public BinaryTree(char[] ch,int index){
        root=create(ch,index);
    }
    //添加元素
    public void add(int data){
        TreeNode newNode=new TreeNode(data);
        if(root==null){
            root=newNode;
            return;
        }
        TreeNode cur=root;
        while(true){
            if(newNode.value<cur.value){
                if(cur.left==null){
                    cur.left=newNode;
                    return;
                }else {
                    cur=cur.left;
                }
            }else{
                if(cur.right==null){
                    cur.right=newNode;
                    return;
                }else{
                    cur=cur.right;
                }
            }
        }
    }
    //将数组表示法转换为链表表示法
    public TreeNode create(char[] arr,int index){
        if(index>=arr.length){
            return null;
        }else{
            TreeNode tmpNode=new TreeNode((int)(arr[index]));
            tmpNode.left=create(arr,2*index);
            tmpNode.right=create(arr,2*index+1);
            return tmpNode;
        }
    }
    //判断表达式如何运算的方法声明
    public int condition(char ch,int n1,int n2){
        switch(ch){
            case '+': return n1+n2;
            case '-': return n1-n2;
            case '*': return n1*n2;
            case '/': return n1/n2;
            case '%': return n1%n2;
            default: return -1;
        }
    }
    //计算二叉运算树的值
    public int answer(TreeNode root){
        int first=0;
        int second=0;
        if(root.left==null&&root.right==null){
            return Character.getNumericValue((char)root.value);
        }else{
            first=answer(root.left);
            second=answer(root.right);
            return condition((char)root.value,first,second);
        }
    }
    //中序表示法
    public void inOrder(TreeNode root){
        if(root!=null){
            inOrder(root.left);
            System.out.print((char)root.value+" ");
            inOrder(root.right);
        }
    }
    //后序表示法
    public void postOrder(TreeNode root){
        if(root!=null){
            postOrder(root.left);
            postOrder(root.right);
            System.out.print((char)root.value+" ");
        }
    }
    //前序表示法
    public void preOrder(TreeNode root){
        if(root!=null){
            System.out.print((char)root.value+" ");
            preOrder(root.left);
            preOrder(root.right);
        }
    }
}

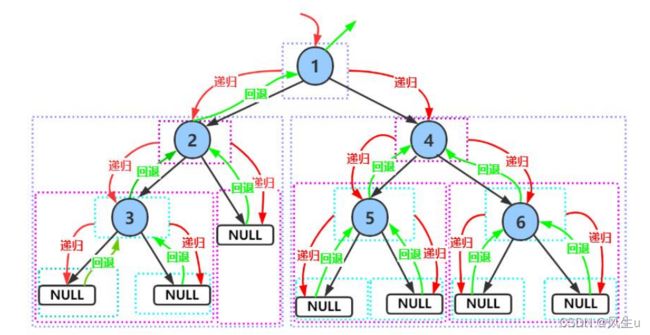
八种遍历方式

所谓遍历(Traversal)是指沿着某条搜索路线，依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题(比如：打印节点内容、节点内容加1)。 遍历是二叉树上最重要的操作之一，是二叉树上进
行其它运算之基础。

在遍历二叉树时，如果没有进行某种约定，每个人都按照自己的方式遍历，得出的结果就比较混乱，如果按照某种规则进行约定，则每个人对于同一棵树的遍历结果肯定是相同的。如果N代表根节点，L代表根节点的左子树，R代表根节点的右子树，则根据遍历根节点的先后次序有以下遍历方式：

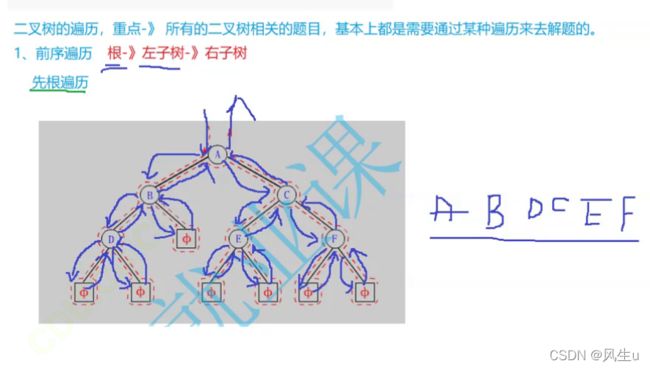
1. NLR：前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点—>根的左子树—>根的右子树。
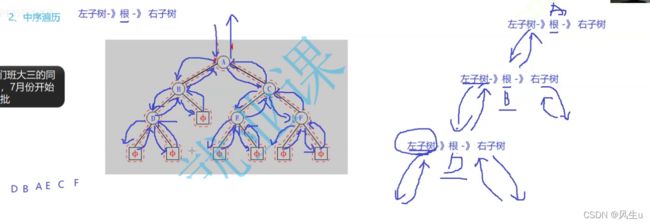
2. LNR：中序遍历(Inorder Traversal)——根的左子树—>根节点—>根的右子树。
3. LRN：后序遍历(Postorder Traversal)——根的左子树—>根的右子树—>根节点。

由于被访问的结点必是某子树的根，所以N(Node）、L(Left subtree）和R(Right subtree）又可解释为根、根
的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。

前序遍历递归实现

//前序遍历
    public void preOrder1(TreeNode root){
        if(root!=null){
            System.out.print(root.value+" ");
            preOrder1(root.left);//遍历左子树
            preOrder1(root.right);//遍历右子树
        }
    }

前序遍历非递归实现

解法一

利用堆栈的性质

 //前序遍历非递归1
    public void preOrder2(TreeNode cur){

        Stack<TreeNode> stack=new Stack<>();
        while(cur!=null||!stack.isEmpty()){
            while(cur!=null){
                stack.add(cur);
                System.out.print(cur.value+" ");
                cur=cur.left;
            }
            cur=stack.pop();
            cur=cur.right;
        }
    }

解法二

将元素按照前序遍历的顺序压入栈中，再依次弹出即可

  //前序遍历非递归2
    public void preOrder3(TreeNode cur){
        Stack<TreeNode> stack=new Stack<>();
        stack.add(cur);
        while(!stack.isEmpty()){
            cur=stack.pop();
            System.out.print(cur.value+" ");
            if(cur.right!=null)
                stack.add(cur.right);
            if(cur.left!=null)
                stack.add(cur.left);
        }
    }

中序遍历递归实现

 //中序遍历
    public void inOrder1(TreeNode root){
        if(root!=null){
            inOrder1(root.left);//处理左子树
            System.out.print(root.value+" ");
            inOrder1(root.right);//处理右子树
        }
    }

中序遍历非递归实现

和前序遍历的非递归实现一样，只不过是交换了打印顺序。

    //中序遍历非递归
    public void inOrder2(TreeNode cur){
        Stack<TreeNode> stack=new Stack<>();
        while(cur!=null||!stack.isEmpty()){
            while(cur!=null){
                stack.add(cur);
                cur=cur.left;
            }
            cur=stack.pop();
            System.out.print(cur.value+" ");
            cur=cur.right;
        }
    }

后序遍历递归实现

 //后序遍历
    public void postOrder1(TreeNode root){
        if(root!=null){
            postOrder1(root.left);//处理左子树
            postOrder1(root.right);//处理右子树
            System.out.print(root.value+" ");
        }
    }

后序遍历非递归实现

后序遍历较为复杂，需要用到栈的性质，且用 cur 来判断打印树叶，用 pre 来记录左或右节点来判断是否打印父节点

    public void postOrder2(TreeNode cur){
        if(cur==null)
            return;

        Stack<TreeNode> stack=new Stack<>();
        TreeNode pre=null;
        stack.add(cur);
        while(!stack.isEmpty()){
            cur=stack.peek();
            if((cur.left==null&&cur.right==null)||(pre!=null&&(pre==cur.left||pre==cur.right))){ 
                System.out.print(cur.value+" ");
                stack.pop();
                pre=cur;
            }else{
                if(cur.right!=null)
                    stack.add(cur.right);
                if(cur.left!=null)
                    stack.add(cur.left);
            }
        }
    }

层序遍历递归实现

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> result = new ArrayList<List<Integer>>();
        helper(root, 0, result);
        return result;
    }

    public void helper(TreeNode root, int level, List<List<Integer>> lists) {
        if (root == null) {
            return;
        }
        if (lists.size() < level + 1) {
            lists.add(new ArrayList<Integer>());
        }
        lists.get(level).add(root.val);
        helper(root.left, level + 1, lists);
        helper(root.right, level + 1, lists);
    }
}

层序遍历非递归实现

利用队列先进先出的性质即可。

    //层序遍历非递归
    public void levelOrder(TreeNode cur){
        LinkedList<TreeNode> queue=new LinkedList<>();
        queue.add(cur);
        while(!queue.isEmpty()){
            cur=queue.pop();
            System.out.print(cur.value+" ");
            if(cur.left!=null)
                queue.add(cur.left);
            if(cur.right!=null)
                queue.add(cur.right);
        }
    }

线索化二叉树

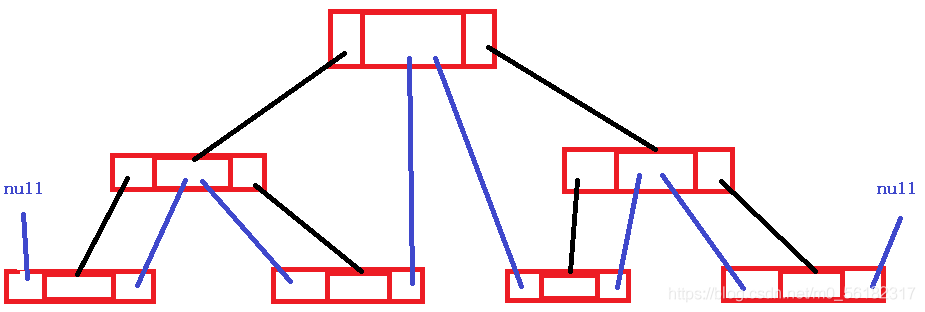
学过链表的读者肯定存在双向链表的，也就是节点相连两个节点之间相互指引，那么二叉树是否也可以通过特定的遍历方式变成特殊的“双向链表”呢？
答案是肯定的。

我们选定一种遍历方式时，遍历到节点A时，遍历A前一个节点叫做节点A的前驱节点，遍历节点A过后，所遍历到的下一个节点叫节点A的后继节点。

中序遍历线索化二叉树及其遍历

先定义一个结点类

public class TreeNode {
    int value;
    TreeNode left;
    TreeNode right;
    boolean lef=false;
    boolean rig=false;
    public TreeNode(){}
    public TreeNode(int data){
        this.value=data;
        left=null;
        right=null;
    }
}

实现中序线索化二叉树

    //中序线索化二叉树
    public void inThreadOrder(TreeNode root) {
        if (root == null) {
            return;
        }
        //处理左子树
        inThreadOrder(root.left);
        if (root.left == null) {
            root.left = pre;
            root.lef = true;
        }
        //前一个节点的后继结点指向当前节点
        if (pre != null && pre.right == null) {
            pre.right = root;
            pre.rig = true;
        }
        pre = root;
        inThreadOrder(root.right);
    }

从后继节点开始遍历

    //中序遍历线索二叉树，按照后继方式遍历
    public void inOrderBlack() {
        TreeNode cur = root;
        while (cur != null && !cur.lef) {
            cur = cur.left;
        }
        while (cur != null) {
            System.out.print(cur.value + " ");
            if (cur.rig) {
                cur = cur.right;
            } else {
                cur = cur.right;
                while (cur != null && !cur.lef)
                    cur = cur.left;
            }
        }
    }

从前驱结点开始遍历

    //中序遍历线索二叉树，按照前驱方式遍历
    public void inOrderBefore() {
        TreeNode cur = root;
        while (cur.right != null && !cur.rig)
            cur = cur.right;
        while (cur != null) {
            System.out.print(cur.value + " ");
            if (cur.lef) {
                cur = cur.left;
            } else {
                cur = cur.left;
                while (cur.right != null && !cur.rig)
                    cur = cur.right;
            }
        }
    }

先定义一个节点类

public class TreeNode {
    int value;
    TreeNode left;
    TreeNode right;
    boolean lef=false;
    boolean rig=false;
    public TreeNode(){}
    public TreeNode(int data){
        this.value=data;
        left=null;
        right=null;
    }
}

前序线索化二叉树

    //前序遍历线索化二叉树
    public void preOrderBinaryTrree(TreeNode root) {
        if (root == null)
            return;
        //左指针为空，将左指针指向前驱节点
        if (root.left == null) {
            root.left = pre;
            root.lef = true;
        }
        //将前一个节点的后继节点指向当前节点
        if (pre != null && pre.right == null) {
            pre.right = root;
            root.rig = true;
        }

        pre = root;

        if (!root.lef)
            preOrderBinaryTrree(root.left);
        if (!root.rig)
            preOrderBinaryTrree(root.right);
    }

遍历前序线索化二叉树

 //前序遍历线索二叉树
    public void preOrderblack() {
        TreeNode cur = root;
        while (cur != null) {
            while (!cur.lef) {
                System.out.println(cur.value + " ");
                cur = cur.left;
            }
            System.out.println(cur.value + " ");
            cur = cur.right;
        }
    }

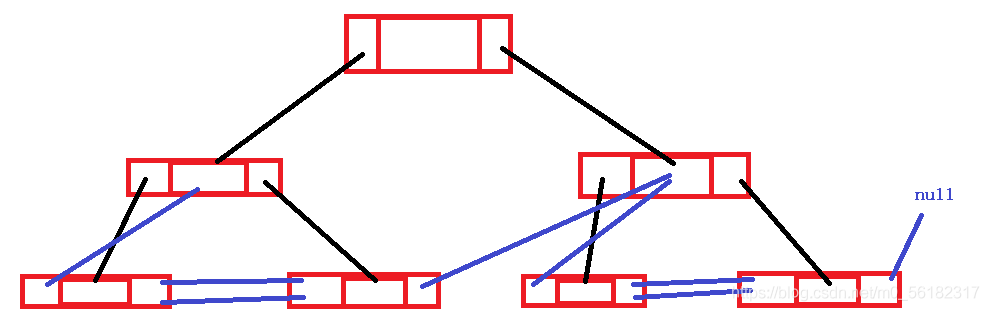
后序线索化二叉树

后序线索化二叉树的节点类

后序线索化二叉树创建的节点类，与前面有所不同，需要一个parent记录父节点

public class TreeNode {
    int value;
    TreeNode left;
    TreeNode right;
    TreeNode parent;
    boolean lef=false;
    boolean rig=false;
    public TreeNode(){}
    public TreeNode(int data){
        this.value=data;
        left=null;
        right=null;
    }
}

实现后序线索化二叉树

    //后序遍历线索化二叉树
    public void postThreadOrder(TreeNode root) {
        if (root == null)
            return;
        //处理左子树
        postThreadOrder(root.left);
        //处理右子树
        postThreadOrder(root.right);

        if (root.left == null) {
            root.left = pre;
            root.lef = true;
        }
        if (pre != null && pre.right == null) {
            pre.right = root;
            pre.rig = true;
        }
        pre = root;
    }

遍历后序线索化二叉树

    //遍历后序遍历线索化的二叉树
    public void postOrderBinaryTree() {
        pre = null;
        TreeNode cur = root;
        while (cur != null && !cur.lef)
            cur = cur.left;

        while (cur != null) {
            if (cur.lef) {
                System.out.println(cur.value + " ");
                pre = cur;
                cur = cur.right;
            } else {
                if (cur.right == pre) {

                    System.out.println(cur.value + " ");

                    if(cur==root)
                        return;

                    pre=cur;
                    cur=cur.parent;
                }else{
                    if(cur==root&&cur.right==null)
                        return;

                        cur=cur.right;
                        while(cur!=null&&!cur.lef)
                            cur=cur.left;
                }
            }
        }
    }

数组实现

通数组的下标一样，可以将二叉树的各节点下标化

添加元素,利用数组建立二叉搜索树

可以发现规律，左子树索引值为父节点索引值2+1
右子树索引值为父节点索引值2+2
故有：

        //添加元素
        public void add(){
            int level=1;
            for(int i=0;i<data.length;i++){
                for(level=1;btree[level]!=0; ){
                    if(data[i]<btree[level])
                        level=level*2;
                    else
                        level=level*2+1;
                }
                btree[level]=data[i];
            }
        }

遍历数组实现的二叉树

因为数组是连续存储的，所以直接打印就行。

 //遍历二叉树
        public void ergodic(){
            System.out.println("二叉树的内容");
            for(int i=1;i<btree.length;i++)
                System.out.print(btree[i]+" ");
            System.out.println();
        }

整体代码实现

public class BinaryTreeByArray {
        int[] data;
        int[] btree=new int[300];
        public BinaryTreeByArray(int[] arr){
            data=arr;
        }
        //添加元素
        public void add(){
            int level=1;
            for(int i=0;i<data.length;i++){
                for(level=1;btree[level]!=0; ){
                    if(data[i]<btree[level])
                        level=level*2;
                    else
                        level=level*2+1;
                }
                btree[level]=data[i];
            }
        }
        //遍历二叉树
        public void ergodic(){
            System.out.println("二叉树的内容");
            for(int i=1;i<btree.length;i++)
                System.out.print(btree[i]+" ");
            System.out.println();
        }
}

归总

package 二叉树链表实现及遍历方法和基本方法;

import java.util.*;

public class BinaryTreeByLink {
    public TreeNode root;

    //添加节点
    public void add(int data) {
        TreeNode newNode = new TreeNode(data);
        //建立树根
        if (root == null) {
            root = newNode;
            return;
        }
        TreeNode cur = root;
        while (true) {
            if (newNode.value < cur.value) {
                if (cur.left == null) {
                    cur.left = newNode;
                    return;
                } else {
                    cur = cur.left;
                }
            } else {
                if (cur.right == null) {
                    cur.right = newNode;
                    return;
                } else {
                    cur = cur.right;
                }
            }
        }
    }
    //二叉树的遍历

    //前序遍历
    public void preOrder1(TreeNode root) {
        if (root != null) {
            System.out.print(root.value + " ");
            preOrder1(root.left);
            preOrder1(root.right);
        }
    }

    //前序遍历非递归1
    public void preOrder2(TreeNode cur) {

        Stack<TreeNode> stack = new Stack<>();
        while (cur != null || !stack.isEmpty()) {
            while (cur != null) {
                stack.add(cur);
                System.out.print(cur.value + " ");
                cur = cur.left;
            }
            cur = stack.pop();
            cur = cur.right;
        }
    }

    //前序遍历非递归2
    public void preOrder3(TreeNode cur) {
        Stack<TreeNode> stack = new Stack<>();
        stack.add(cur);
        while (!stack.isEmpty()) {
            cur = stack.pop();
            System.out.print(cur.value + " ");
            if (cur.right != null)
                stack.add(cur.right);
            if (cur.left != null)
                stack.add(cur.left);
        }
    }

    //中序遍历
    public void inOrder1(TreeNode root) {
        if (root != null) {
            inOrder1(root.left);
            System.out.print(root.value + " ");
            inOrder1(root.right);
        }
    }

    //中序遍历非递归
    public void inOrder2(TreeNode cur) {
        Stack<TreeNode> stack = new Stack<>();
        while (cur != null || !stack.isEmpty()) {
            while (cur != null) {
                stack.add(cur);
                cur = cur.left;
            }
            cur = stack.pop();
            System.out.print(cur.value + " ");
            cur = cur.right;
        }
    }

    //后序遍历
    public void postOrder1(TreeNode root) {
        if (root != null) {
            postOrder1(root.left);
            postOrder1(root.right);
            System.out.print(root.value + " ");
        }
    }

    //后序遍历非递归
    public void postOrder2(TreeNode cur) {
        if (cur == null)
            return;

        Stack<TreeNode> stack = new Stack<>();
        TreeNode pre = null;
        stack.add(cur);
        while (!stack.isEmpty()) {
            cur = stack.peek();
            if ((cur.left == null && cur.right == null) || (pre != null && (pre == cur.left || pre == cur.right))) {
                System.out.print(cur.value + " ");
                stack.pop();
                pre = cur;
            } else {
                if (cur.right != null)
                    stack.add(cur.right);
                if (cur.left != null)
                    stack.add(cur.left);
            }
        }
    }

    void postOrderNor(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        TreeNode prev = null;

        while (cur != null || !stack.isEmpty()) {
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }

            TreeNode top = stack.peek();
            //如果当前节点的右子树被打印过 或者 遍历过  直接弹出了
            if (top.right == null || top.right == prev) {
                stack.pop();
                System.out.print(top.value+" ");
                prev = top;//记录一下 最近一次打印的节点
            } else {
                cur = top.right;
            }
        }
    }


    //层序遍历递归
    public void levelOrder1(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        if (root == null) return;
        queue.offer(root);
        while (!queue.isEmpty()) {
            TreeNode cur = queue.poll();
            System.out.print(cur.value + " ");
            if (cur.left != null) {
                queue.offer(cur.left);
            }
            if (cur.right != null) {
                queue.offer(cur.right);
            }
        }
    }

    //层序遍历：分层打印
    public List<List<Integer>> levelOrder3(TreeNode root) {

        List<List<Integer>> ret = new ArrayList<>();
        if (root == null) return ret;

        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);

        while (!queue.isEmpty()) {
            int size = queue.size();//这个值代表 当前层有多少个节点
            List<Integer> list = new ArrayList<>();
            while (size != 0) {
                TreeNode cur = queue.poll();
                //list.add(cur.val); 你在OJ写的时候  需要放开这个注释
                if (cur.left != null) {
                    queue.offer(cur.left);
                }
                if (cur.right != null) {
                    queue.offer(cur.right);
                }
                size--;//1 0
            }
            ret.add(list);
        }
        return ret;
    }

    //层序遍历非递归
    public void levelOrder2(TreeNode cur) {
        LinkedList<TreeNode> queue = new LinkedList<>();
        queue.add(cur);
        while (!queue.isEmpty()) {
            cur = queue.pop();
            System.out.print(cur.value + " ");
            if (cur.left != null)
                queue.add(cur.left);
            if (cur.right != null)
                queue.add(cur.right);
        }
    }


    /**
     *获取树中节点的个数
     */
/*
    int count = 0;
    int size1(TreeNode root) {
        if(root == null) {
            return 0;
        }
        count++;
        size1(root.left);
        size1(root.right);
        return count;
    }
    */

    /**
     * 子问题思路
     *
     * @param root
     * @return
     */
    int size(TreeNode root) {
        if (root == null) {
            return 0;
        }
        return size(root.left) + size(root.right) + 1;
    }

    /**
     * 获取叶子节点的个数
     * 遍历思路：
     */
    static int leafCount = 0;
/*    void getLeafNodeCount(TreeNode root) {
        if(root == null) {
            return;
        }
        if(root.left == null && root.right == null) {
            leafCount ++;
        }
        getLeafNodeCount(root.left);
        getLeafNodeCount(root.right);
    }*/

    /**
     * 获取叶子节点的个数
     * 子问题思路
     *
     * @param root
     * @return
     */

    void getLeafNodeCount(TreeNode root) {
        if (root == null) {
            return;
        }
        if (root.left == null && root.right == null) {
            leafCount++;
        }
        getLeafNodeCount(root.left);
        getLeafNodeCount(root.right);
    }

    /**
     * 获取叶子节点的个数
     * 子问题思路
     *
     * @param root
     * @return
     */
    int getLeafNodeCount2(TreeNode root) {
        if (root == null) {
            return 0;
        }
        if (root.left == null && root.right == null) {
            //当前的root是叶子节点
            return 1;
        }
        return getLeafNodeCount2(root.left) + getLeafNodeCount2(root.right);
    }

    /**
     * 获取第K层节点的个数
     * 子问题思路：
     */
    int getKLevelNodeCount(TreeNode root, int k) {
        if (root == null || k <= 0) {
            return 0;
        }
        if (k == 1) {
            return 1;
        }
        return getKLevelNodeCount(root.left, k - 1) + getKLevelNodeCount(root.right, k - 1);
    }

    /**
     * 获取二叉树的高度
     * 时间复杂度：O(n)
     * 空间复杂度：O()
     */
    int getHeight(TreeNode root) {
        if (root == null) return 0;
        int leftHeight = getHeight(root.left);
        int rightHeight = getHeight(root.right);
        return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
    }

    //递归次数容易太多，超出时间限制
    int getHeight2(TreeNode root) {
        if (root == null) return 0;
        return getHeight2(root.left) > getHeight2(root.right) ? getHeight2(root.left) + 1 : getHeight2(root.right) + 1;
    }


    /**
     * 检测值为value的元素是否存在
     */
    TreeNode find(TreeNode root, char val) {
        if (root == null) return null;
        if (root.value == val) return root;

        TreeNode ret = find(root.left, val);
        if (ret != null) {
            return ret;
        }
        ret = find(root.right, val);
        if (ret != null) {
            return ret;
        }
        return null;
    }

    /**
     * 是不是完全二叉树
     *
     * @param root
     * @return
     */
    boolean isCompleteTree(TreeNode root) {
        if (root == null) return true;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            TreeNode cur = queue.poll();
            if (cur != null) {
                queue.offer(cur.left);
                queue.offer(cur.right);
            } else {
                break;
            }
        }

        while (!queue.isEmpty()) {
            TreeNode top = queue.peek();
            if (top != null) {
                return false;
            }
            queue.poll();
        }
        return true;
    }

    //判断两个二叉树是否完全相等
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if (p == null && q != null || p != null && q == null) {
            return false;
        }
        if (p == null && q == null) {
            return true;
        }
        if (p.value != q.value) {
            return false;
        }
        //p != null && q!= null && p.val == q.val
        return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
    }

    //判断一个树是否是该树的子树
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if (root == null || subRoot == null) {
            return false;
        }
        //等价于上面
//        if(root == null && subRoot != null) {
//            return false;
//        }
//        if(root != null && subRoot == null) {
//            return false;
//        }
//        if(root == null && subRoot == null) {
//            return true;
//        }


        //判断根节点是不是两棵相同的树
        if (isSameTree(root, subRoot)) {
            return true;
        }

        //subroot是不是root的左子树
        if (isSubtree(root.left, subRoot)) {
            return true;
        }

        //subroot是不是root的右子树
        if (isSubtree(root.right, subRoot)) {
            return true;
        }
        return false;
    }

    /**
     * 判断是否是平衡二叉树
     * 时间复杂度：O(N^2)
     */
    public boolean isBalanced(TreeNode root) {
        if (root == null) return true;
        int left = getHeight(root.left);
        int right = getHeight(root.right);
        return Math.abs(left - right) <= 1 && isBalanced(root.left) && isBalanced(root.right);
    }

    /**
     * 判断是否是平衡二叉树
     * 时间复杂度：O(n)
     */
    public boolean isBalanced2(TreeNode root) {
        if (root == null) return true;

        return getHeight3(root) >= 0;
    }

    int getHeight3(TreeNode root) {
        if (root == null) return 0;
        int leftHeight = getHeight(root.left);
        int rightHeight = getHeight(root.right);
        if (leftHeight >= 0 && rightHeight >= 0 && Math.abs(leftHeight - rightHeight) <= 1) {
            return Math.max(leftHeight, rightHeight) + 1;
        } else {
            return -1;
        }
    }

    //检查二叉树是否轴对称。
    public boolean judge(TreeNode leftTree, TreeNode rightTree) {
        if (leftTree != null && rightTree == null) return false;

        if (leftTree == null && rightTree != null) return false;

        if (leftTree == null && rightTree == null) return true;

        if (leftTree.value != rightTree.value) return false;

        return judge(leftTree.left, rightTree.right) && judge(leftTree.right, rightTree.left);
    }

    public boolean isSymmetric(TreeNode root) {
        if (root == null) {
            return true;
        } else {
            return judge(root.left, root.right);
        }
    }

    //求最小公共祖先 理解不了！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        // LCA 问题
        if (root == null) {
            return root;
        }
        if (root == p || root == q) {
            return root;
        }
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);
        if (left != null && right != null) {
            return root;
        } else if (left != null) {
            return left;
        } else if (right != null) {
            return right;
        }
        return null;
    }

//    求最小公共祖先 栈模拟链表实现
    public boolean getPath(TreeNode root,TreeNode node,Stack<TreeNode> stack){
        if(root==null||node==null) return false;

        stack.push(root);

        if(root==node) return true;

        boolean flag=getPath(root.left,node,stack);
        if(flag==true) return true;

        flag=getPath(root.right,node,stack);
        if(flag==true) return true;

        stack.pop();
        return false;
    }

    public TreeNode lowestCommonAncestor2(TreeNode root, TreeNode p, TreeNode q) {
        Stack<TreeNode> stack1=new Stack<>();
        Stack<TreeNode> stack2=new Stack<>();

        getPath(root,p,stack1);
        getPath(root,q,stack2);

        Stack<TreeNode> stackmax=stack1.size()>stack2.size() ? stack1:stack2;
        Stack<TreeNode> stackmin= stackmax==stack1 ? stack2 : stack1;

        while(!stackmax.isEmpty() && !stackmin.isEmpty() && stackmax.size()!=stackmin.size()){
            stackmax.pop();
        }

        while(!stackmax.isEmpty() && !stackmin.isEmpty()){
            if(stackmax.peek()==stackmin.peek()){
                return stackmax.peek();
            }else{
                stackmax.pop();
                stackmin.pop();
            }
        }
        return null;
    }



    /**
     * 二叉搜索树 转换为排序的双向链表
     */

    TreeNode prev = null;

    public void inorder(TreeNode pCur) {
        if(pCur == null) return;
        inorder(pCur.left);

        //打印
        pCur.left = prev;
        if(prev != null) {
            prev.right = pCur;
        }
        prev = pCur;
        //System.out.print(pCur.val+" ");
        inorder(pCur.right);
    }

    public TreeNode Convert(TreeNode pRootOfTree) {

        if(pRootOfTree == null) return null;

        inorder(pRootOfTree);

        TreeNode head = pRootOfTree;
        while(head.left != null) {
            head = head.left;
        }
        return head;
    }

    /*
    根据前中序遍历创建二叉树
     */
    public int preIndex = 0;

    public TreeNode createTreeByPandI(int[] preorder, int[] inorder,int inbegin,int inend) {

        if(inbegin > inend) {
            //如果满足这个条件  说明 没有左树 或者 右树了
            return null;
        }
        TreeNode root = new TreeNode(preorder[preIndex]);
        //找到根在中序遍历的位置
        int rootIndex = findIndexOfI(inorder,inbegin,inend,preorder[preIndex]);
        if(rootIndex == -1) {
            return null;
        }
        preIndex++;
        //分别创建 左子树 和 右子树
        root.left = createTreeByPandI(preorder,inorder,inbegin,rootIndex-1);
        root.right = createTreeByPandI(preorder,inorder,rootIndex+1,inend);
        return root;
    }

    private int findIndexOfI(int[] inorder,int inbegin,int inend,int key) {

        for(int i = inbegin; i <= inend;i++) {
            if(inorder[i] == key) {
                return i;
            }
        }
        return -1;
    }

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if(preorder == null || inorder == null) return null;

        return createTreeByPandI(preorder,inorder,0,inorder.length-1);
    }


/*
    根据前中后遍历创建二叉树
    public int postIndex = 0;

    public TreeNode createTreeByPandI(int[] inorder, int[] postorder,int inbegin,int inend) {

        if(inbegin > inend) {
            //如果满足这个条件  说明 没有左树 或者 右树了
            return null;
        }
        TreeNode root = new TreeNode(postorder[postIndex]);
        //找到根在中序遍历的位置
        int rootIndex = findIndexOfI(inorder,inbegin,inend,postorder[postIndex]);
        if(rootIndex == -1) {
            return null;
        }
        postIndex--;
        //分别创建右子树 和  左子树
        root.right = createTreeByPandI(inorder,postorder,rootIndex+1,inend);

        root.left = createTreeByPandI(inorder,postorder,inbegin,rootIndex-1);
        return root;
    }
    private int findIndexOfI(int[] inorder,int inbegin,int inend,int key) {

        for(int i = inbegin; i <= inend;i++) {
            if(inorder[i] == key) {
                return i;
            }

        }
        return -1;
    }
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        if(postorder == null || inorder == null) return null;
        postIndex = postorder.length-1;

        return createTreeByPandI(inorder,postorder,0,inorder.length-1);
    }*/
}