【思特奇杯·云上蓝桥-算法集训营】第1周
1题 跑步训练
1题 跑步训练
问题描述
小明要做一个跑步训练,初始时,小明充满体力,体力值计为 10000。
如果小明跑步,每分钟损耗 600 的体力。
如果小明休息,每分钟增加 300 的体力。
体力的损耗和增加都是 均匀变化的。
小明打算跑一分钟、休息一分钟、再跑一分钟、再休息一分钟……如此循环。
如果某个时刻小明的体力到达 0,他就停止锻炼, 请问小明在多久后停止锻炼。
为了使答案为整数,请以秒为单位输出答案,答案中只填写数,不填写单位。
答案提交
这是一道结果填空题,你只需要算出结果后提交即可。
本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
小学奥数题
total = 10000
consume = 10
i = 0
while total > 600:
total = total - 600 + 300
i += 1
min1 = total/consume
res = int(min1 + i*120)
print(res)
答案:3880
2题 阶乘约数
2题 阶乘约数
问题描述
定义阶乘 n! = 1 × 2 × 3 × ··· × n。
请问 100! (100 的阶乘)有多少个约数。
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。
本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
n = 100
# 因为数不大,就用最普通的方法统计质数了。
p = [2]
for i in range(3, n + 1):
j = 2
while j < i:
if i % j == 0:
break
j += 1
else:
p.append(i)
m = {}
for i in p:
m[i] = 1 # 每个质数初始为 1,代表不选这个质数的可能。
for i in range(2, n + 1): # 遍历 [2, 100]
x = i
for j in p: # 遍历质数,将每个被乘数都质因数分解一下。
# (比如 6 分解成 2*3 ,12 分解成 2*2*3)
if j > x:
break
while x % j == 0:
x //= j
# 让对应的质数个数 + 1
m[j] += 1
s = 1
# 所有质因子的个数相乘,就是约数个数了。
for i in m.values():
s *= i
print(s)
答案:39001250856960000
3题 出栈次序
3题 出栈次序
问题描述
X星球特别讲究秩序,所有道路都是单行线。
一个甲壳虫车队,共16辆车,按照编号先后发车,夹在其它车流中,缓缓前行。
路边有个死胡同,只能容一辆车通过,是临时的检查站,如图所示。
X星球太死板,要求每辆路过的车必须进入检查站,也可能不检查就放行,也可能仔细检查。
如果车辆进入检查站和离开的次序可以任意交错。
那么,该车队再次上路后,可能的次序有多少种?
为了方便起见,假设检查站可容纳任意数量的汽车。
显然,如果车队只有1辆车,可能次序1种;2辆车可能次序2种;3辆车可能次序5种。
现在足足有16辆车啊,亲!需要你计算出可能次序的数目。
答案提交
这是一个整数,请通过浏览器提交答案,不要填写任何多余的内容(比如说明性文字)。
卡特兰数应用(卡特兰数百度百科)
我们把n个元素的出栈个数的记为f(n), 那么对于1,2,3, 我们很容易得出:
f(1)= 1 即 1
f(2)= 2 即 12、21
f(3)= 5 即 123、132、213、321、231
f(4) = f(3) +f(2) * f(1) + f(1) * f(2) + f(3) 即有14种
求卡特兰数的公式之一,用h(n)表示卡特兰数的第n项,其中h(0)=1,h(1)=1
h(n)= h(0)*h(n-1)+h(1)*h(n-2) + … + h(n-1)h(0) (n>=2)
用递推求卡特兰数:
def f(i):
sum = 0
if i == 0 or i == 1:
return 1
else:
for j in range(i):
sum += f(j)*f(i-j-1)
return sum
a = f(16)
print(a)
答案35357670
4题 哥德巴赫分解
哥德巴赫猜想认为:不小于4的偶数都可以表示为两个素数的和。
你不需要去证明这个定理,但可以通过计算机对有限数量的偶数进行分解,验证是否可行。
实际上,一般一个偶数会有多种不同的分解方案,我们关心包含较小素数的那个方案。
对于给定数值范围,我们想知道这些包含较小素数方案中最大的素数是多少。
比如,100以内,这个数是19,它由98的分解贡献。
你需要求的是10000以内,这个数是多少?
注意,需要提交的是一个整数,不要填写任何多余的内容(比如,说明性的文字)
先两次for循环,然后判断是不是质数
res = 0
n = 10000
def isPrimeNumber(num):
num = int(num)
for i in range(2, num):
if num % i == 0:
return False
return True
for i in range(4, n, 2):
for j in range(2, int(i / 2)):
if isPrimeNumber(j) and isPrimeNumber(i - j):
res = max(res, j)
break
print(res)
答案:173
5题 图书排列
5题 图书排列
题目描述
将编号为1~10的10本书排放在书架上,要求编号相邻的书不能放在相邻的位置。
请计算一共有多少种不同的排列方案。
注意,需要提交的是一个整数,不要填写任何多余的内容。
使用itertools包中的permutations可以迭代出所有的排列可能,然后再筛选
import itertools
def define(a):
for i in range(9):
if abs(a[i]-a[i+1]) == 1:
return False
return True
num = [1,2,3,4,5,6,7,8,9,10]
res = 0
for i in itertools.permutations(num, 10):
if define(i):
res += 1
print(res)
答案:479306
6题 猴子分香蕉
5只猴子是好朋友,在海边的椰子树上睡着了。这期间,有商船把一大堆香蕉忘记在沙滩上离去。
第1只猴子醒来,把香蕉均分成5堆,还剩下1个,就吃掉并把自己的一份藏起来继续睡觉。
第2只猴子醒来,重新把香蕉均分成5堆,还剩下2个,就吃掉并把自己的一份藏起来继续睡觉。
第3只猴子醒来,重新把香蕉均分成5堆,还剩下3个,就吃掉并把自己的一份藏起来继续睡觉。
第4只猴子醒来,重新把香蕉均分成5堆,还剩下4个,就吃掉并把自己的一份藏起来继续睡觉。
第5只猴子醒来,重新把香蕉均分成5堆,哈哈,正好不剩!
请计算一开始最少有多少个香蕉。
需要提交的是一个整数,不要填写任何多余的内容。
暴力比较快一点
n = 6
while True:
if n % 5 == 1:
a = (n - 1) / 5 * 4
if int(a) % 5 == 2:
b = (a - 2) / 5 * 4
if int(b) % 5 == 3:
c = (b - 3) / 5 * 4
if int(c) % 5 == 4:
d = (c - 4) / 5 * 4
if int(d) % 5 == 0 and d != 0:
break
n += 1
print(n)
答案:16
7题 稍小分数
回到小学----
真分数:分子小于分母的分数
既约分数:分子分母互质,也就是说最大公约数是1
x星球数学城的入口验证方式是:
屏幕上显示一个真分数,需要你快速地找到一个比它小的既约分数,要求这个分数越大越好。
同时限定你的这个分数的分母不能超过100。
def gcd(a,b):
if b == 0:
return a
return gcd(b, a % b)
a=7
b=13
max_a = 0
max_b = 1
for n in range(100,1,-1):
for m in range(n-1,0,-1):
if m * b < a and gcd(m, n) == 1:
if m*max_b>n*max_a:
max_a = m
max_b = n
break
print(max_a,max_b)
8题 excel地址
时间限制:1.0s 内存限制:256.0MB
问题描述
Excel单元格的地址表示很有趣,它使用字母来表示列号。
比如,
A表示第1列,
B表示第2列,
Z表示第26列,
AA表示第27列,
AB表示第28列,
BA表示第53列,
....
当然Excel的最大列号是有限度的,所以转换起来不难。
如果我们想把这种表示法一般化,可以把很大的数字转换为很长的字母序列呢?
本题目即是要求对输入的数字, 输出其对应的Excel地址表示方式。
样例输入
26
样例输出
Z
样例输入
2054
样例输出
BZZ
数据规模和约定
我们约定,输入的整数范围[1,2147483647]
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
注意:
main函数需要返回0;
只使用ANSI C/ANSI C++ 标准;
不要调用依赖于编译环境或操作系统的特殊函数。
所有依赖的函数必须明确地在源文件中 #include 类似于10进制转26进制
x = [chr(i) for i in range(65,91)]
n = int(input())
res = []
while n != 0:
if n % 26 == 0:
res.append(26)
n = n // 26 - 1
else:
res.append(n % 26)
n = n//26
for i in range(len(res)):
res[i] = x[res[i]-1]
res.reverse()
print(''.join(res))
9题 日期问题
小明正在整理一批历史文献。这些历史文献中出现了很多日期。小明知道这些日期都在1960年1月1日至2059年12月31日。令小明头疼的是,这些日期采用的格式非常不统一,有采用年/月/日的,有采用月/日/年的,还有采用日/月/年的。更加麻烦的是,年份也都省略了前两位,使得文献上的一个日期,存在很多可能的日期与其对应。
比如02/03/04,可能是2002年03月04日、2004年02月03日或2004年03月02日。
给出一个文献上的日期,你能帮助小明判断有哪些可能的日期对其对应吗?
输入
一个日期,格式是"AA/BB/CC"。 (0 <= A, B, C <= 9)
输出
输出若干个不相同的日期,每个日期一行,格式是"yyyy-MM-dd"。多个日期按从早到晚排列。
样例输入
02/03/04
样例输出
2002-03-04
2004-02-03
2004-03-02
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
这个确实不会,网上看大佬思路来的
#日期问题
n = input()
list1 = []
a = n.split("/")
def wang1(x,y,z):
if int(y)!=2:
if int(y) in [1,3,5,7,8,10,12] and int(z) <= 31:
list1.append("20%s-%s-%s" % (x, y, z))
elif int(y) in [4,6,9,11] and int(z)<=30:
list1.append("20%s-%s-%s" % (x, y, z))
if int(y)==2:
if (int("20%s"%x)%4==0 and int("20%s"%x)%100!=0) or int("20%s"%x)%400==0:
if int(z)<=29:
list1.append("20%s-%s-%s"%(x,y,z))
elif int(z)<=28:
list1.append("20%s-%s-%s" % (x, y, z))
def wang2(x,y,z):
if int(y)!=2:
if int(y) in [1,3,5,7,8,10,12] and int(z) <= 31:
list1.append("19%s-%s-%s" % (x, y, z))
elif int(y) in [4,6,9,11] and int(z)<=30:
list1.append("19%s-%s-%s" % (x, y, z))
elif (int("19%s"%x)%4==0 and int("19%s"%x)%100!=0) or int("19%s"%x)%400==0:
if int(z)<=29:
list1.append("19%s-%s-%s"%(x,y,z))
elif int(z)<=28:
list1.append("19%s-%s-%s" % (x, y, z))
if 0<int(a[1])<=12 and int(a[0])<=59:
wang1(x=a[0],y=a[1],z=a[2])
elif 0<int(a[1])<=12 and int(a[0])>59:
wang2(x=a[0], y=a[1], z=a[2])
if 0<int(a[0])<=12 and int(a[2])<=59 and int(a[1])<=31:
wang1(x=a[2], y=a[0], z=a[1])
elif 0<int(a[0])<=12 and int(a[2])>59 and int(a[1])<=31:
wang2(x=a[2], y=a[0], z=a[1])
if 0<int(a[1])<=12 and int(a[2])<=59 and 0<int(a[0])<=31:
wang1(x=a[2], y=a[1], z=a[0])
elif 0 < int(a[1]) <= 12 and int(a[2]) > 59 and 0<int(a[0])<=31 :
wang2(x=a[2], y=a[1], z=a[0])
temp = list(set(list1))
temp.sort()
for i in temp:
print(i)
10题 整数划分
对于一个正整数n的划分,就是把n变成一系列正整数之和的表达式。注意,分划与顺序无关,例如6=5+1.跟6=1+5是同一种分划,另外,这个整数本身也是一种分划。
例如:对于正整数n=5,可以划分为:
1+1+1+1+1
1+1+1+2
1+1+3
1+2+2
2+3
1+4
5
输入描述
输入一个正整数n
输出描述
输出n整数划分的总数k
输入样例
5
输出样例
7
def div(n, m):
if n == 1 or m == 1:
return 1
elif n < m:
return div(n, n)
elif n == m:
return 1 + div(n, n-1)
else:
return div(n, m - 1) + div(n - m, m)
n = int(input())
if n >= 1:
print(div(n, n))
11题 一步之遥
从昏迷中醒来,小明发现自己被关在X星球的废矿车里。
矿车停在平直的废弃的轨道上。
他的面前是两个按钮,分别写着“F”和“B”。
小明突然记起来,这两个按钮可以控制矿车在轨道上前进和后退。
按F,会前进97米。按B会后退127米。
透过昏暗的灯光,小明看到自己前方1米远正好有个监控探头。
他必须设法使得矿车正好停在摄像头的下方,才有机会争取同伴的援助。
或许,通过多次操作F和B可以办到。
矿车上的动力已经不太足,黄色的警示灯在默默闪烁...
每次进行 F 或 B 操作都会消耗一定的能量。
小明飞快地计算,至少要多少次操作,才能把矿车准确地停在前方1米远的地方。
请填写为了达成目标,最少需要操作的次数。
注意,需要提交的是一个整数,不要填写任何无关内容(比如:解释说明等
暴力两层for循环
for i in range(1, 100):
for j in range(1, 100):
if i * 97 - j * 127 == 1:
num = i + j
print(num)
break
答案:97
12题 机器人塔
X星球的机器人表演拉拉队有两种服装,A和B。
他们这次表演的是搭机器人塔。
类似:
A
B B
A B A
A A B B
B B B A B
A B A B B A
队内的组塔规则是:
A 只能站在 AA 或 BB 的肩上。
B 只能站在 AB 或 BA 的肩上。
你的任务是帮助拉拉队计算一下,在给定A与B的人数时,可以组成多少种花样的塔。
输入一行两个整数 M 和 N,空格分开(0<M,N<500),分别表示A、B的人数,保证人数合理性。
要求输出一个整数,表示可以产生的花样种数。
例如:
用户输入:
1 2
程序应该输出:
3
再例如:
用户输入:
3 3
程序应该输出:
4
资源约定:
峰值内存消耗 < 256M
CPU消耗 < 1000ms
无论A,B给多少人,能堆出来的塔的层数一定是唯一确定的。先从最后一层开始把最后一层的所有可能遍历出来,然后在用递推的方式一层一层的递归。
a=list(map(int,input().split()))
s=sum(a)
ab=[1,2]
for i in range(2,1000):
if s==((i+1)*i)//2:
o=i
break
try:
c=[[0 for i1 in range(o+1)]for i in range(o+1)]
con=0
def ck(i,r,l):
if a[i]-1>=0:
c[r][l]=ab[i]
a[i]-=1
if l>=r:
dfs(r-1,0)
else:
dfs(r,l+1)
c[r][l]=0
a[i]+=1
def dfs(r,l):
global con
if r==-1:
con+=1
return
elif r==o-1:
for i in range(2):
ck(i,r,l)
elif c[r+1][l]==c[r+1][l+1]:
ck(0,r,l)
elif c[r+1][l]!=c[r+1][l+1]:
ck(1,r,l)
dfs(o-1,0)
print(con)
except:
print(0)
13题 七星填空
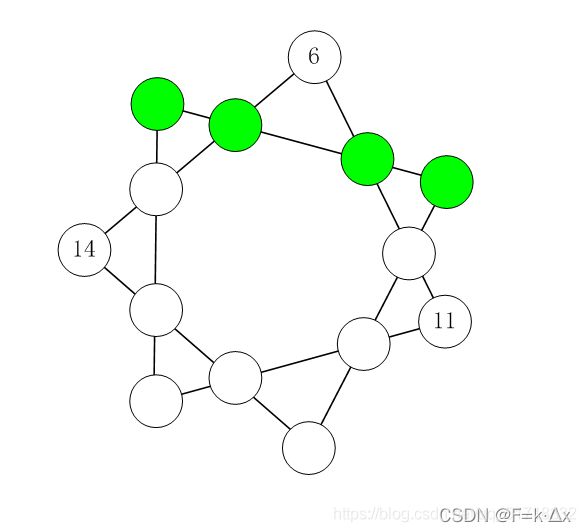
如下图所示。在七角星的 14 个节点上填入 1 ~ 14的数字,不重复,不遗漏。 要求每条直线上的四个数字之和必须相等。
图片描述
图中已经给出了 3 个数字。 请计算其它位置要填充的数字,答案唯一。
填好后,请输出绿色节点的 4 个数字(从左到右,用空格分开)。
from itertools import *
for i in permutations([1,2,3,4,5,7,8,9,10,12,13]):
#还有11个
num=i[0]+i[1]+i[2]+i[3]
if num==6+i[1]+i[4]+14:
if num==6+i[2]+i[5]+11:
if num==14+i[6]+i[7]+i[9]:
if num==i[3]+i[5]+i[8]+i[9]:
if num==i[10]+i[7]+i[8]+11:
if num==i[0]+i[4]+i[6]+i[10]:
print(i[0],i[1],i[2],i[3])
答案:10 3 9 8