基于 eigen 实现神经网络的反向传播算法（2）

       前文展示了基于 Martin H. Hagan 的《神经网络设计》 ch11 所述的多层圣经网络的基本反向传播算法（SDBP）的实现和部分测试结果。在对其例题函数的训练测试中我也发现了该文CH12提到的速度不佳及收敛性问题。其中收敛问题根本上影响的算法的有效性。

本文将展示该书CH12提到的改进算法，改进的目标即速度与收敛性。改进算法有以下几种

• 引入动量的反传算法  MOBP  （启发式优化技术）
• 可变学习速度的反传算法  VLBP  （启发式优化技术）
• 共轭梯度反传算法   CGBP（数值优化技术）
• LevenBurg Marquardt反传算法 LMBP（数值优化技术）

代码依然基于前文代码修改并兼容基本算法。由于网络结构图与之前相同，此处省略。

     MOBP

     首先实现导入动量 gamma的反传算法，基于SDBP算法导入动量十分简单。实现如下：

在原有每层数据结构中增加 deltaW和deltaB，用于记录上一次计算中 W的变化量。

/**
*  定义每一层神经网络的参数定义
*/
template 
struct tag_NN_LAY_PARAM {
	T(*func)(T); //  限定函数指针，
	T(*dfunc)(T); //  限定函数指针， // Derivative
    MATRIX  W;
    MATRIX  deltaW; // for MOBP
    VECTOR  B;
    VECTOR  deltaB;
	VECTOR  N;
	VECTOR  A;
	VECTOR  S;
};
typedef struct tag_NN_LAY_PARAM   NN_LAYER_PARAM_F;
typedef struct tag_NN_LAY_PARAM   NN_LAYER_PARAM_D;

在原算法中增加 gamma 加权，当gamma为0时，算法退化为 SDBP。

/**
*   P 11.2.2  反向传播算法 BP Back Propagation
*   最终公式参考 （ 11.41 ~ 11.47 ）
*  S1:     A[m+1] = p
*          A[m+1] = f[m+1]( W[m+1]*A[m]+b[m+1] ),        m=0,1,2,...,M-1
*  S2:     S[M]   = -2F[M]'(n[M])( T-A[M] )
*          S[m]   = F[m+1]'(n[m])*(W[m+1]的转置)*S[m+1], m=M-1,...,2,1
*  S3:     W[m](k+1) = W[m](k) - a*S[m]*(A[m-1]的转置)
*          b[m](k+1) = b[m](k) - a*S[m]
*
*  Input Paramenters :
*    [in]     P  : m x n 样本输入矩阵， 每列代表样本数据，有n个样本
*                  P x m个向量的取值仅限 { -1, +1 }
*    [in]     T  : p x n 目标矩阵，每列代表目标数据，有n个目标
*    [in/out] lay_list : 每层网络参数
*    [out]    e     :
*    [in]     gamma : MOBP 算法需要动量改进参数，缺省值为 0.8  (12.2.2)
*                     引入动量参数前，相当于该值为 0
*    [in]     alpha : 修正步长,缺省值为 0.01
*  internal var:
*    W : matrix [p][m]       T = W * P
*    e : matrix [p][1]
*  output :*/

bool BackPropagation_multi_lay_process(
        const Eigen::VectorXf &P,
        const Eigen::VectorXf &T,
        std::list &lay_list, //
        Eigen::VectorXf *e,
        float gamma,
        float alpha)
{
	/* 1.0 正向传播
	A0 -> A1 -> .... -> Am
	*/

    auto next_A = P;
    for (auto iter = lay_list.begin(); iter != lay_list.end(); ++iter) {
        iter->N = (iter->W * next_A + iter->B);
        iter->A = iter->N.unaryExpr(std::ref(iter->func));
        next_A = iter->A;
    }
	/* 2.0 反向传播 
     *   S(m) = -2*dervFm(Nm)*(T-Am);
     */
    {
        auto iter = lay_list.rbegin();

        iter->S = -2 * iter->N.unaryExpr(std::ref(iter->dfunc)).asDiagonal().toDenseMatrix()*(T - iter->A);
        Eigen::MatrixXf next_WS = iter->W.transpose()*iter->S;
        if( e )
        {
            *e = T - iter->A;
        }
        for (iter++; iter != lay_list.rend(); ++iter) {
            iter->S = iter->N.unaryExpr(std::ref(iter->dfunc)).asDiagonal().toDenseMatrix() * next_WS;
            next_WS = iter->W.transpose() * iter->S;
        }
    }
	/*  3.0 更新权值和偏移值 */
    auto last_a = P;
    for (auto iter = lay_list.begin(); iter != lay_list.end(); ++iter) {
		iter->deltaW = gamma * iter->deltaW - (1.0f - gamma) * alpha * iter->S*last_a.transpose();
		iter->W = iter->W + iter->deltaW;
		iter->deltaB = gamma * iter->deltaB - (1.0f - gamma) * alpha * iter->S;
		iter->B = iter->B + iter->deltaB;
        last_a = iter->A;
    }

    return true;
}

VLBP 可变学习速度的反传算法

 VLBP在 SDBP基础上加入以下原则来调整参数

头文件 BackPropagation_VLBP.h 定义如下

#pragma once

#include 
#include "BackPropagation.h"

class BackPropagation_VLBP
{
public:
    BackPropagation_VLBP();

    void reset();
    void process( const Eigen::VectorXf &P,
                  const Eigen::VectorXf &T,
                  const TRAIN_SET_F &PT );

    const NN_SIMPLE_LAYER_LIST_F getLayerList() const;
    bool calc(const Eigen::VectorXf &P, Eigen::VectorXf *T);

    NN_LAYER_LIST_F m_layer_list;
private:
    void init();

private:
    Eigen::VectorXf e;

    float m_curr_err;
    float m_err_limit; /* 1% ~ 5% */
    float m_fixed_learn_speed;
    float m_learn_speed;
    float m_learn_speed_decrease_factor;
    float m_learn_speed_increase_factor;
    float m_fixed_momentum;
    float m_real_momentum;
};

源文件 BackPropagation_VLBP.cpp 定义如下，调用成员函数 process()一次算一次迭代。

#include "BackPropagation_VLBP.h"

float m_err_limit;
float m_learn_speed_scalor;
BackPropagation_VLBP::BackPropagation_VLBP()
    : m_err_limit( 0.05 ),
      m_fixed_learn_speed(0.1),
      m_learn_speed_decrease_factor(0.7),
      m_learn_speed_increase_factor(1.05),
      m_fixed_momentum(0.5)
{
    init();
}

void BackPropagation_VLBP::init()
{
    m_round = 0;
    m_learn_speed = m_fixed_learn_speed;
    m_real_momentum = m_fixed_momentum;
    m_curr_err = 10000000000000.f;
/*    if( func )
    {
        func( m_layer_list );
    }
    */
}
void BackPropagation_VLBP::reset()
{
    init();
}

const NN_SIMPLE_LAYER_LIST_F BackPropagation_VLBP::getLayerList() const
{
    NN_SIMPLE_LAYER_LIST_F layerlist;

    for( auto iter = m_layer_list.begin();
         iter != m_layer_list.end();
         iter++ )
    {
        NN_SIMPLE_LAYER_F sl;
        sl.W = iter->W;
        sl.B = iter->B;
        sl.func = iter->func;
        layerlist.push_back(sl);
    }
    return layerlist;
}

/**
 *  P 11.2.2( SDBP )+ P 12.2.2-2 (VLBP)
 *    可变学习速度的反传算法  VLBP
 *   P 11.2.2  反向传播算法 BP Back Propagation
 *   最终公式参考 （ 11.41 ~ 11.47 ）
 *  S1:     A[m+1] = p
 *          A[m+1] = f[m+1]( W[m+1]*A[m]+b[m+1] ),        m=0,1,2,...,M-1
 *  S2:     S[M]   = -2F[M]'(n[M])( T-A[M] )
 *          S[m]   = F[m+1]'(n[m])*(W[m+1]的转置)*S[m+1], m=M-1,...,2,1
 *  S3:     W[m](k+1) = W[m](k) - a*S[m]*(A[m-1]的转置)
 *          b[m](k+1) = b[m](k) - a*S[m]
 *
 *  Input Paramenters :
 *    [in]     P  : m x n 样本输入矩阵， 每列代表样本数据，有n个样本
 *                  P x m个向量的取值仅限 { -1, +1 }
 *    [in]     T  : p x n 目标矩阵，每列代表目标数据，有n个目标
 *    [in/out] lay_list : 每层网络参数
 *    [out]    e     :
 *    [in]     gamma : MOBP 算法需要动量改进参数，缺省值为 0.8  (12.2.2)
 *                     引入动量参数前，相当于该值为 0
 *    [in]     alpha : 修正步长,缺省值为 0.01
 *  internal var:
 *    W : matrix [p][m]       T = W * P
 *    e : matrix [p][1]
 *  output :
 */
void BackPropagation_VLBP::process(
        const Eigen::VectorXf &P, const Eigen::VectorXf &T,
        const TRAIN_SET_F &PT)
{
    NN_SIMPLE_LAYER_LIST_F simple_layer_list;

    BackPropagation_base( P, T, m_layer_list, &e );
    BackPropagation_updateDeltaWB( P, m_layer_list );
    BackPropagation_nextNN( m_layer_list, simple_layer_list, m_learn_speed );
    double err = calc_MSE(PT, simple_layer_list);

	printf(" compare err = %2.2f, m_curr_err = %2.2f \r\n", err, m_curr_err);
    if ( err < m_curr_err )
    {
        if( m_learn_speed < m_fixed_learn_speed )
        {
            m_learn_speed = m_fixed_learn_speed;
        } else {
            m_learn_speed *= m_learn_speed_increase_factor;
        }
        m_real_momentum = m_fixed_momentum;
        BackPropagation_updateWB( P, m_layer_list, 0, m_learn_speed * m_learn_speed_increase_factor );
//        m_curr_err = err;
		printf(" update WB ");
	} else if( err < m_curr_err*(1+m_err_limit) )
    {
        m_learn_speed = m_fixed_learn_speed * m_learn_speed_decrease_factor;
        m_real_momentum = m_fixed_momentum;
        BackPropagation_updateWB( P, m_layer_list, 0, m_learn_speed );
		printf(" update WB ");
    } else {
        m_learn_speed *= m_learn_speed_decrease_factor;
        m_real_momentum = 0.0f;
    }
    m_curr_err = err;
    m_round++;
	printf(" m_learn_speed = %2.2f, m_real_momentum = %2.2f \r\n", m_learn_speed, m_real_momentum);

}

bool BackPropagation_VLBP::calc(
        const Eigen::VectorXf &P, Eigen::VectorXf *T)
{
    bool ret = calculate_multi_lay_process(P, m_layer_list );
    if( NULL != T )
    {
        *T = m_layer_list.rbegin()->A;
    }
    return ret;
}

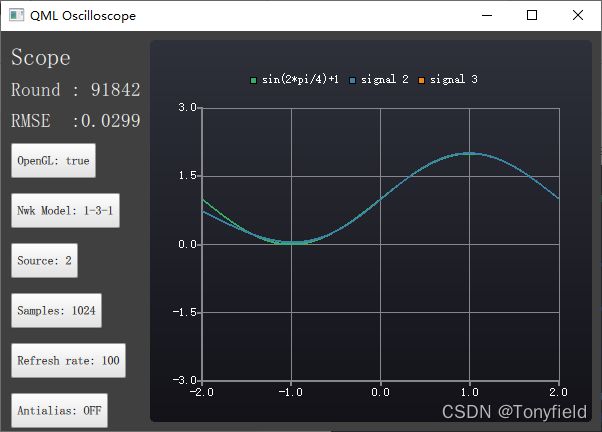
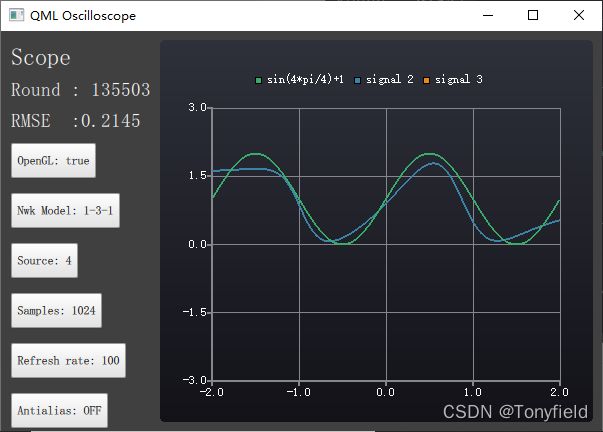
计算结果如下

 

    对于有2个周期的波形，目前调试得到的 1-3-1 VLBP过程还是没能做到 图11-12中那样的准确匹配的结果。：-（