数据结构与算法之查找-经典题目解析
目录
35. 搜索插入位置
202. 快乐数
205. 同构字符串
242. 有效的字母异位词
290. 单词规律
349. 两个数组的交集
350. 两个数组的交集 II
410. 分割数组的最大值
451. 根据字符出现频率排序
540. 有序数组中的单一元素
1. 两数之和
15. 三数之和
16. 最接近的三数之和
18. 四数之和
49. 字母异位词分组
149. 直线上最多的点数
219. 存在重复元素 II
220. 存在重复元素 III
447. 回旋镖的数量
454. 四数相加 II
35. 搜索插入位置
难度 简单
题目：给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。
你可以假设数组中无重复元素。
思路：
- 首先排序数组，可以考虑使用二分法。
- 然后在循环的过程中，将左右边界
beg和end逐渐向中间靠拢。 - 最后在循环过程中，若找到目标值，直接返回；若最后
beg和end相遇，仍未找到目标值，那插入的位置即为 beg。
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
# 定义两个数组的指针
beg = 0
end = len(nums) - 1
# 使用二分法遍历数组
while beg <= end:
mid = (beg + end) // 2
if target > nums[mid]:
# 当target大于nums[mid]时，更新beg指针
beg = mid + 1
elif target < nums[mid]:
# 当target小于nums[mid]时，更新end指针
end = mid - 1
else:
# 当target等于nums[mid]时，返回目标值索引
return mid
# 遍历结束未找到目标值时，需要插入的位置保存在beg指针中，直接返回即可
return beg复杂度分析：
- 时间复杂度：
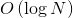，其中 N 为数组的长度。二分查找所需的时间复杂度为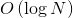。 - 空间复杂度：
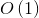，我们只需要常数空间存放若干变量。
202. 快乐数
难度 简单
题目：编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」定义为：对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和，然后重复这个过程直到这个数变为 1，也可能是无限循环但始终变不到 1。如果可以变为 1，那么这个数就是快乐数。
如果 n 是快乐数就返回 True ；不是，则返回 False 。
思路：
- 寻找快乐数时会出现的情况：
- 最终会得到1；
- 最终会进入循环；
- 值会越来越大，最后接近无穷大。
- 对于 3 位数的数字，它不可能大于 243。这意味着它要么被困在 243 以下的循环内，要么跌到 1。4 位或 4 位以上的数字在每一步都会丢失一位，直到降到 3 位为止。所以我们知道，最坏的情况下，算法可能会在 243 以下的所有数字上循环，然后回到它已经到过的一个循环或者回到 1。但它不会无限期地进行下去，所以我们排除第三种情况。
- 初始化集合 s，用于存放中间生成的结果。
- 计算每个位置上数字的平方和，并加入集合 s。
- 重复上述过程，直到n等于 1，返回 True；或新生成的数字已经存在于集合 s，返回 False。
class Solution:
def isHappy(self, n: int) -> bool:
"""集合法"""
s = set() # 保存中间结果
# n等于1，或n在集合s中时，退出循环
while n != 1 and n not in s:
s.add(n)
n = sum(map(lambda x: int(x) ** 2, str(n))) # 数位分离，求平方和
return n == 1复杂度分析：
- 时间复杂度：
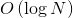
- 查找给定数字的下一个值的成本为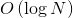，因为我们正在处理数字中的每位数字，而数字中的位数由
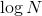给定。 - 要计算出总的时间复杂度，我们需要仔细考虑循环中有多少个数字，它们有多大。
- 我们在上面确定，一旦一个数字低于 243，它就不可能回到 243 以上。因此，我们就可以用 243 以下最长循环的长度来代替 243，不过，因为常数无论如何都无关紧要，所以我们不会担心它。
- 对于高于 243 的 N，我们需要考虑循环中每个数高于 243 的成本。通过数学运算，我们可以证明在最坏的情况下，这些成本将是
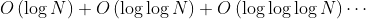。幸运的是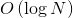，是占主导地位的部分，而其他部分相比之下都很小（总的来说，它们的总和小于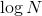），所以我们可以忽略它们。
- 查找给定数字的下一个值的成本为
- 空间复杂度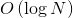：。与时间复杂度密切相关的是衡量我们放入集合中的数字以及它们有多大的指标。对于足够大的 N，大部分空间将由 N 本身占用。我们可以很容易地优化到
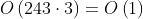，方法是只保存集合中小于 243 的数字，因为对于较高的数字，无论如何都不可能返回到它们。
思路：
- 初始化两个指针，快指针 fast 和慢指针 slow，慢指针每次前进 1 个节点，快指针每次前进 2 个节点。
- 若 n 是一个快乐数，则快指针会率先到达数字 1。
- 若 n 不是一个快乐数，则快指针和慢指针将会在某一个数字上相遇。
class Solution:
def isHappy(self, n: int) -> bool:
"""快慢指针法"""
def inner(m):
return sum(map(lambda x: int(x) ** 2, str(m))) # 数位分离，求平方和
# 初始化两个指针
slow = n # 慢指针每次前进1个节点
fast = inner(n) # 快指针每次前进2个节点
# 若慢指针与快指针在一个节点相遇，说明存在循环，否则快指针将率先到达数字1
while fast != 1 and slow != fast:
slow = inner(slow)
fast = inner(inner(fast))
return fast == 1复杂度分析：
- 时间复杂度：
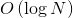
- 如果没有循环，那么快指针将先到达 1，慢指针将到达链表中的一半。我们知道最坏的情况下，成本是
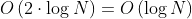。 - 一旦两个指针都在循环中，在每个循环中，快指针将离慢指针更近一步。一旦快指针落后慢指针一步，他们就会在下一步相遇。假设循环中有 k 个数字。如果他们的起点是相隔 k−1 的位置（这是他们可以开始的最远的距离），那么快指针需要 k−1 步才能到达慢指针，这对于我们的目的来说也是不变的。因此，主操作仍然在计算起始 n 的下一个值，即。
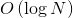- 如果没有循环，那么快指针将先到达 1，慢指针将到达链表中的一半。我们知道最坏的情况下，成本是
- 空间复杂度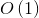：，指针只需要常数的额外空间。
205. 同构字符串
难度 简单
题目：给定两个字符串 s 和 t，判断它们是否是同构的。
如果 s 中的字符可以被替换得到 t ，那么这两个字符串是同构的。
所有出现的字符都必须用另一个字符替换，同时保留字符的顺序。两个字符不能映射到同一个字符上，但字符可以映射自己本身。
思路：
- 用字典将 s 与 t 中各字符的映射关系进行记录。
- 遍历字符串：
- 若 s[i] 已经有了映射，那么检测 s[i] 的映射是否等于 t[i]，不相等则不同构。
- 若 s[i] 还没有映射，但是 t[i] 已经被映射过了，由于题目规定两个字符不能映射到同一字符，因此不同构。
- 若 s[i] 还没有映射，且 t[i] 也没有被映射过，那么建立 s[i] 到 t[i] 的映射。
- 遍历正常结束，说明 s 与 t 是同构的。
class Solution:
def isIsomorphic(self, s: str, t: str) -> bool:
d = dict() # 保存映射关系
for i in range(len(s)):
if s[i] in d:
if d[s[i]] != t[i]:
return False # 若s[i]与t[i]的映射关系不匹配，则返回False
else:
if t[i] in d.values():
return False # 若s[i]不存在映射关系，而t[i]存在映射关系，则返回False
d[s[i]] = t[i] # 若s[i]与t[i]之间不存在映射关系，则添加
return True复杂度分析：
- 时间复杂度：
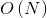，只进行了一次循环操作。 - 空间复杂度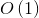：，尽管我们使用了额外的空间，但是空间的复杂性是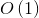，因为无论 N 有多大，字典的大小都不超过26（26个字母）。
242. 有效的字母异位词
难度 简单
题目：给定两个字符串 s 和 t ，编写一个函数来判断 t 是否是 s 的字母异位词。
思路：
- 为了判断字母异位词，我们可以计算两个字符串中每个字母的出现次数并进行比较。
- 首先判断两个字符串长度是否相等，不相等则两个字符串不是字母异位词。
- 若相等，则初始化一个字典，并遍历字符串 s 和 t。
- s 负责在对应位置增加，t 负责在对应位置减少。
- 如果字典中的值没有小于0的，则二者是字母异位词。
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
# 若两字符串长度不一致，则返回False
if len(s) != len(t):
return False
# 遍历s，统计字符出现次数
d = dict()
for i in s:
if d.get(i):
d[i] += 1
else:
d[i] = 1
# 遍历t，使对应字符的出现次数递减
for i in t:
if d.get(i) is None:
return False # 若t中的字符i不在字典d中，则返回False
d[i] -= 1
if d.get(i) < 0:
return False # 若t中的字符i使字典中i的出现次数递减至0以下，则返回False
return True复杂度分析：
- 时间复杂度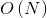：，因为需要对字符串进行一次遍历。
- 空间复杂度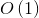：，尽管我们使用了额外的空间，但是空间的复杂性是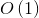，因为无论 N 有多大，字典的大小都不超过26（26个字母）。
290. 单词规律
难度 简单
题目：给定一种规律 pattern 和一个字符串 str ，判断 str 是否遵循相同的规律。
这里的 遵循 指完全匹配，例如， pattern 里的每个字母和字符串 str 中的每个非空单词之间存在着双向连接的对应规律。
思路：
- 首先判断
pattern的字符长度与str的非空单词长度是否相同。 - 然后用字典来记录
pattern中的字符与str中的非空单词之间的映射关系。 - 接下来与“205. 同构字符串”的解题思路类似。
class Solution:
def wordPattern(self, pattern: str, str: str) -> bool:
# 若两者的长度不一致，则返回False
if len(pattern) != len(str.split()):
return False
d = dict() # 保存映射关系
str = str.split()
for i in range(len(pattern)):
if pattern[i] in d:
if d[pattern[i]] != str[i]:
return False # 若pattern[i]与str[i]的映射关系不匹配，则返回False
else:
if str[i] in d.values():
return False # 若pattern[i]不存在映射关系，而str[i]存在映射关系，则返回False
d[pattern[i]] = str[i] # 若pattern[i]与str[i]之间不存在映射关系，则添加
return True复杂度分析：
- 时间复杂度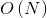：，只进行了一次循环操作。
- 空间复杂度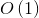：，尽管我们使用了额外的空间，但是空间的复杂性是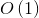，因为无论 N 有多大，字典的大小都不超过26（26个字母）。
349. 两个数组的交集
难度 简单
题目：给定两个数组，编写一个函数来计算它们的交集。
思路：
- 先将 nums1 和 nums2 转换为集合。
- 然后计算两个集合的交集。
- 最后将计算的结果转换为列表。
class Solution:
def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
return list(set(nums1) & set(nums2))复杂度分析：
- 时间复杂度：
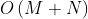，其中 M和N是数组的长度。将nums1转换为集合需要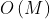
的时间，类似地，将 nums2转换为集合需要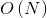的时间。最坏情况下是
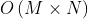。 - 空间复杂度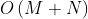：，最坏的情况是数组中的所有元素都不同。
350. 两个数组的交集 II
难度 简单
题目：给定两个数组，编写一个函数来计算它们的交集。
输出结果中每个元素出现的次数，应与元素在两个数组中出现次数的最小值一致。
可以不考虑输出结果的顺序。
思路：
- 首先遍历 nums1 并记录出现的数字和出现的次数。
- 然后遍历 nums2，判断数字在字典中是否存在：
- 若存在，且出现次数大于0，则将数字添加到 res，并将其次数减1。若次数减至0，则将其键值对从字典中移除。
- 先遍历较短的数字可以优化空间复杂度。
class Solution:
def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:
# 先遍历较短的数组可以优化空间复杂度
if len(nums1) > len(nums2):
return self.intersect(nums2, nums1)
res = list() # 保存结果
d = dict() # 记录nums1中出现的数字以及出现次数
for i in nums1:
if d.get(i):
d[i] += 1
else:
d[i] = 1
for i in nums2:
# 若d中存在数字i，且i的出现次数大于0时，添加到res中，并令出现次数减1
# 若d中的i对应的值减至0，则将其键值对移除字典
if d.get(i):
res.append(i)
d[i] -= 1
if d[i] == 0:
d.pop(i)
return res复杂度分析：
- 时间复杂度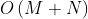：，其中 M 和 N 分别是两个数组的长度。需要遍历两个数组并对字典进行操作，字典操作的时间复杂度是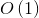，因此总时间复杂度与两个数组的长度和呈线性关系。
- 空间复杂度：
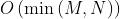，其中 M 和 N 分别是两个数组的长度。对较短的数组进行字典的操作，字典的大小不会超过较短的数组的长度。
410. 分割数组的最大值
难度 困难
题目：给定一个非负整数数组和一个整数 m，你需要将这个数组分成 m 个非空的连续子数组。设计一个算法使得这 m 个子数组各自和的最大值最小。
思路：
- 子数组和的最大值的取值范围：
![\left [ max \left ( nums \right ),sum\left ( nums \right ) \right ]](http://img.e-com-net.com/image/info8/5228ca5edd2c4502a14975aaf66ae721.gif)
。 - 贪心地模拟分割过程：遍历数组，计算数字和的最大值不超过 mid 时所对应的子数组的数量 count。
- 若 count > m，说明划分的子数组多了，mid 较小，需要提高取值的下界，即 left = mid + 1。
- 若 count <= m，说明划分的子数组少了，mid 较大（或正好），需要降低取值的上界，即 right = mid
class Solution:
def splitArray(self, nums: List[int], m: int) -> int:
def inner(x):
# 计算数组和的最大值不超过x时所对应的子数组的数量count
sum_, count = 0, 1
for num in nums:
if sum_ + num > x:
count += 1
sum_ = num
else:
sum_ += num
return count > m
left = max(nums) # 子数组的最大值的下界
right = sum(nums) # 子数组的最大值的上界
# 二分查找
while left < right:
mid = (left + right) // 2
if inner(mid):
left = mid + 1 # 划分的子数组多了，mid偏小
else:
right = mid # 划分的子数组少了，mid偏大（或正好）
return left复杂度分析：
- 时间复杂度：
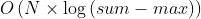，其中 sum 表示数组 nums 中所有元素的和，max 表示数组所有元素的最大值。每次二分查找时，需要对数组进行一次遍历，时间复杂度为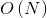，因此总时间复杂度是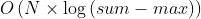。 - 空间复杂度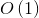：，只使用到常数个临时变量。
451. 根据字符出现频率排序
难度 中等
题目：给定一个字符串，请将字符串里的字符按照出现的频率降序排列。
思路：
- 使用 Counter 对字符出现频率进行统计。
- 遍历统计结果，将字符和出现次数相乘。
- 使用 join() 将字符串进行拼接。
from collections import Counter
class Solution:
def frequencySort(self, s: str) -> str:
return ''.join([k * v for k, v in Counter(s).most_common()])540. 有序数组中的单一元素
难度 中等
题目：给定一个只包含整数的有序数组，每个元素都会出现两次，唯有一个数只会出现一次，找出这个数。
思路：
- 前提：
- 我们需要查看中间的元素来判断我们的答案在中间，左边还是右边。
- 我们的数组个数始终是奇数，因为有一个元素出现一次，其余元素出现两次。
- 从中心移除一对元素时，将剩下左子数组和右子数组。
- 与原数组一样，包含单个元素的子数组元素个数必为奇数，不包含单个元素的子数组必为偶数。
- 首先初始化指向数组首尾的指针 left 和 right。
- 然后进行二分搜索将数组搜索空间减半，直到找到单一元素或者仅剩一个元素为止。当搜索空间只剩一个元素，则该元素就是单一元素。
- 循环中，先判断与 mid 处的元素相同的元素位于前面，还是后面，然后移除这一对元素后，判断左右子数组的奇偶，并更新 left 和 right 指针。
- 最后，要么在循环中，mid 处元素与其前后元素都不相同，返回结果；要么循环结束 left == right，返回 nums[left]。
class Solution:
def singleNonDuplicate(self, nums: List[int]) -> int:
# 初始化首尾指针
left = 0
right = len(nums) - 1
# 二分法
while left < right:
mid = (left + right) // 2
is_even = (right - mid) % 2 == 0 # 判断右子数组是否为偶数
if nums[mid] == nums[mid-1]: # mid处的元素与其前一位相同
if is_even:
# 此时，右子数组为偶数，应该在左子数组内搜索
right = mid - 2
else:
# 此时，右子数组为奇数，应该在右子数组内搜索
left = mid + 1
elif nums[mid] == nums[mid+1]: # mid处的元素与其后一位相同
if is_even:
# 此时，右子数组为偶数，但减去mid+1处的元素后为奇数，所以应该在右子数组内搜索
left = mid + 2
else:
# 此时，右子数组为奇数，但减去mid+1处的元素后为偶数，所以应该在左子数组内搜索
right = mid - 1
else:
# mid处的元素与其前后元素都不相同，则直接返回
return nums[mid]
return nums[left]复杂度分析：
- 时间复杂度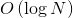：。在每次循环迭代中，我们将搜索空间减少了一半。
- 空间复杂度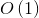：，只使用到常数个临时变量。
思路：
- 前提：
- 对所有偶数索引进行搜索，直到遇到第一个其后元素不相同的索引，该索引处的元素即为单一元素。
- 在检索单个元素后面的偶数索引时，其后都没有它的同一元素。因此，我们可以通过偶数索引确定单个元素在左侧还是右侧。
- 首先初始化指向数组首尾的指针 left 和 right。
- 我们需要确保
mid是偶数，如果为奇数，则将其减1。 - 然后，我们检查
mid的元素是否与其后面的索引处元素相同。若相同，则我们知道mid不是单个元素。且单个元素在mid之后。若不相同，则我们知道单个元素位于mid，或者在mid之前。 - 最后，当 left == right 时，表示当前搜索空间为 1 个元素，那么该元素即为单一元素。
class Solution:
def singleNonDuplicate(self, nums: List[int]) -> int:
# 初始化首尾指针
left = 0
right = len(nums) - 1
# 二分法
while left < right:
mid = (left + right) // 2
# 若mid为奇数时，减1使其为偶数
if mid % 2 == 1:
mid -= 1
if nums[mid] == nums[mid+1]:
# 若mid处元素与其后一位元素相同，则单一元素在右子数组内
left = mid + 2
else:
# 若mid处元素与其后一位元素不相同，则单一元素在左子数组内，或mid处元素即为单一元素
right = mid
return nums[left]复杂度分析：
- 时间复杂度：
。我们仅对元素的一半进行二分搜索。 - 空间复杂度：，只使用到常数个临时变量。
1. 两数之和
难度 简单
题目：给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那 两个 整数，并返回他们的数组下标。
你可以假设每种输入只会对应一个答案。但是，数组中同一个元素不能使用两遍。
思路：
- 前提：两数之和等于目标值，那如果已知一个值 nums[i]，就只需要遍历数组查找另一个值 target - nums[i] 即可。
- 首先初始化一个字典用来保存 nums 中的元素-索引对。
- 然后遍历数组，判断 target - nums[i] 值是否存在字典中。若存在，直接返回两个数的索引；若不存在，则将元素 nums[i] 和对应索引添加到字典。
- 最后，如果遍历结束没有找到两数之和等于目标值，则返回空列表。
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
d = dict() # 保存nums中的元素-索引对
for i in range(len(nums)):
x = target - nums[i]
if d.get(x) is not None:
return [i, d[x]] # 若d中存在x，则直接返回索引
d[nums[i]] = i # 若d中不存在x，则添加
return [] # 若不存在两数之和等于目标值，则返回空列表复杂度分析：
- 时间复杂度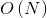：。我们只遍历了包含有 N 个元素的列表一次。在表中进行的每次查找只花费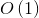的时间。
- 空间复杂度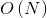：。所需的额外空间取决于字典中存储的元素数量，该字典最多需要存储 N 个元素。
15. 三数之和
难度 中等
题目：给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有满足条件且不重复的三元组。
思路：
- 前提：
- 要使结果“不重复”，首先需要将数组中的元素从小到大进行排序，然后枚举的三元组（a，b，c）满足
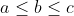。此外，若相邻两次枚举的元素相同，也会造成重复，所以在枚举a，b，c时，我们需要“跳”到下一个不相同的元素。 - 使用三重循环分别枚举a，b，c的时间复杂度为
。若固定前两重循环枚举到的元素 a 和 b，那么只有唯一的 c 满足 a+b+c=0。也就是说，我们可以从小到大枚举 b，同时从大到小枚举 c，即保持第二重循环不变，而将第三重循环变成一个从数组最右端开始向左移动的指针。但是，要注意 b 的指针始终处于 c 的指针的左侧。
- 要使结果“不重复”，首先需要将数组中的元素从小到大进行排序，然后枚举的三元组（a，b，c）满足
- 首先对数组进行排序。
- 然后枚举 a，保证枚举的 a 与上次的不同。初始化 c 的指针，指向数组的最后一个元素。
- 接着枚举 b，保证枚举的 b 与上次的不同。在确保 b 指针处于 c 指针的左侧的前提下，不断移动 c 指针，直到出现下面两种情况：
- b 指针与 c 指针重合，表示没有合适的 b 和 c 使等式 a+b+c=0 成立，可以跳出循环。
- 等式 a+b+c=0 成立，将结果添加至列表 res 中。
- 最后返回 res，即为符合条件的三元组。
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
n = len(nums)
nums.sort() # 排序
res = list() # 保存符合条件的结果
# 枚举a
for a in range(n):
# 枚举的a不能与上次相同
if a > 0 and nums[a] == nums[a-1]:
continue
c = n - 1 # 初始化c的指针
target = -nums[a]
# 枚举b
for b in range(a+1, n):
# 枚举的b不能与上次相同
if b > a+1 and nums[b] == nums[b-1]:
continue
# 需要保证b指针始终处于c指针的左侧
while b < c and nums[b] + nums[c] > target:
c -= 1
# 若指针重合，则表示没有合适的b，c指针使等式a+b+c=0成立
if b == c:
break
# 若等式a+b+c=0成立，则将符合条件的三元组添加至res
if nums[b] + nums[c] == target:
res.append([nums[a], nums[b], nums[c]])
return res复杂度分析：
- 时间复杂度：
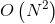，其中 N 是数组 nums 的长度。我们首先需要
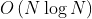的时间对数组进行排序，随后在枚举的过程中，使用一重循环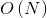枚举 a，一重循环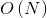枚举 b 和 c，故一共是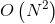。 - 空间复杂度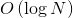：。我们忽略存储答案的空间，额外的排序的空间复杂度为。
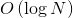16. 最接近的三数之和
难度 中等
题目：给定一个包括 n 个整数的数组 nums 和 一个目标值 target。找出 nums 中的三个整数，使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。
思路：
- 前提：
- 要使结果“不重复”，首先需要将数组中的元素从小到大进行排序，然后枚举的三元组（a，b，c）满足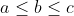。此外，若相邻两次枚举的元素相同，也会造成重复，所以在枚举a，b，c时，我们需要“跳”到下一个不相同的元素。
- 使用三重循环分别枚举a，b，c的时间复杂度为。若固定第一重循环枚举元素 a，然后在 [i+1, n) 范围内枚举 b 和 c，通过三数之和与 target 的差值来更新最接近 target 的三数之和。
- 要使结果“不重复”，首先需要将数组中的元素从小到大进行排序，然后枚举的三元组（a，b，c）满足
- 首先对数组进行排序。
- 然后枚举 a，保证枚举的 a 与上次的不同。初始化 b 和 c 的指针，分别指向数组中 a 的后一个元素和数组的最后一个元素。
- 接着枚举 b 和 c，求三数之和，更新最接近 target 的三数之和，此时有三种情况：
- 三数之和等于 target：直接返回即可。
- 三数之和大于 target：此时向左移动 c 的指针，使三数之和减小，从而更接近 target。
- 三数之和小于 target：此时向右移动 b 的指针，是三数之和增大，从而更接近 target。
- 最后返回最接近 target 的三数之和。
class Solution:
def threeSumClosest(self, nums: List[int], target: int) -> int:
n = len(nums)
nums.sort() # 排序
res = 10 ** 4 # 保存最接近target的三数之和
# 枚举a
for a in range(n):
# 枚举的a不能与上次相同
if a > 0 and nums[a] == nums[a-1]:
continue
b, c = a + 1, n - 1 # 初始化b和c的指针
while b < c:
sum_ = nums[a] + nums[b] + nums[c] # 求三数之和
# 若三数之和等于target，则直接返回
if sum_ == target:
return sum_
# 更新最接近target的三数之和
if abs(sum_ - target) < abs(res - target):
res = sum_
if sum_ > target:
# 若三数之和大于target，则向左移动c的指针
c0 = c - 1
# 枚举的c不能与上次相同
while c0 > b and nums[c0] == nums[c]:
c0 -= 1
c = c0
else:
# 若三数之和小于target，则向右移动b的指针
b0 = b + 1
# 枚举的b不能与上次相同
while b0 < c and nums[b] == nums[b0]:
b0 += 1
b = b0
# 返回最接近target的三数之和
return res复杂度分析：
- 时间复杂度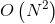：，其中 N 是数组 nums 的长度。我们首先需要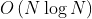的时间对数组进行排序，随后在枚举的过程中，使用一重循环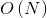枚举 a，双指针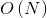枚举 b 和 c，故一共是。
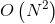- 空间复杂度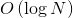：。我们忽略存储答案的空间，额外的排序的空间复杂度为。
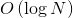18. 四数之和
难度 中等
题目：给定一个包含 n 个整数的数组 nums 和一个目标值 target，判断 nums 中是否存在四个元素 a，b，c 和 d ，使得 a + b + c + d 的值与 target 相等？找出所有满足条件且不重复的四元组。
思路：
- 其思路与“15.三数之和”类似，区别仅是多了一层循环。
class Solution:
def fourSum(self, nums: List[int], target: int) -> List[List[int]]:
n = len(nums)
nums.sort() # 排序
res = list() # 保存所有符合条件的4个元素
# 枚举a
for a in range(n):
# 枚举的a不能与上次相同
if a > 0 and nums[a] == nums[a-1]:
continue
# 枚举b
for b in range(a+1, n):
# 枚举的b不能与上次相同
if b > a+1 and nums[b] == nums[b-1]:
continue
c, d = b + 1, n - 1 # 初始化c和d的指针
while c < d:
sum_ = nums[a] + nums[b] + nums[c] + nums[d] # 求四数之和
# 若四数之和等于target，则将其添加至res，并移动c和d的指针寻找下一个符合条件的元素
if sum_ == target:
res.append([nums[a], nums[b], nums[c], nums[d]])
# 确保枚举的c与上次不同
c0 = c + 1
while c0 < d and nums[c] == nums[c0]:
c0 += 1
c = c0
# 确保枚举的d与上次不同
d0 = d - 1
while d0 > c and nums[d0] == nums[d]:
d0 -= 1
d = d0
elif sum_ > target:
d -= 1 # 若四数之和大于target，则向左移动d的指针
else:
c += 1 # 若四数之和小于target，则向右移动d的指针
# 返回所有符合条件的四元素
return res复杂度分析：
- 时间复杂度：，其中 N 是数组 nums 的长度。我们首先需要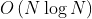的时间对数组进行排序，随后在枚举的过程中，使用一重循环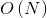枚举 a，使用一重循环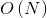枚举 b，一重循环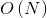枚举 c 和 d，故一共是。
- 空间复杂度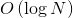：。我们忽略存储答案的空间，额外的排序的空间复杂度为。
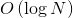49. 字母异位词分组
难度 中等
题目：给定一个字符串数组，将字母异位词组合在一起。字母异位词指字母相同，但排列不同的字符串。
思路：
- 前提：若两个字符串属于字母异位词，那对其字符出现次数进行统计，统计结果应该相同。
- 首先初始化字典用于保存符合条件的异位词。
- 然后遍历 strs，初始化一个长度为 26 的列表，统计 strs 中每个字符串中字符的出现次数。
- 接着将统计结果转换为元组，并添加至字典 res。
- 最后输出分好组的字母异位词。
class Solution:
def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
res = dict() # 保存计数-字母异位词对
for s in strs:
tmp = [0] * 26 # 计数初始化
# 统计字符出现次数
for c in s:
tmp[ord(c) - ord('a')] += 1
# 将统计结果添加至res字典
tmp = tuple(tmp)
if res.get(tmp):
res[tmp].append(s)
else:
res[tmp] = [s]
return list(res.values())复杂度分析：
- 时间复杂度：
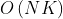，其中 N 是 strs的长度，而 K 是strs中字符串的最大长度。计算每个字符串的字符串大小是线性的，我们统计每个字符串。 - 空间复杂度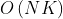：，排序存储在
res中的全部信息内容。
149. 直线上最多的点数
难度 困难
题目：给定一个二维平面，平面上有 n 个点，求最多有多少个点在同一条直线上。
思路：
- 前提：在同一条直线上的任意两点的斜率必定相同。
- 首先，若 points 中的点少于 3，则可以直接返回，因为 1 个点或 2 个点必定能构成直线。
- 然后遍历每个点，计算经过该点的每条直线上出现的点的数量，并记录其中的最大值。在遍历时：
- 使用 same 记录与点 point 相同的点的数量，使用 diff 记录同一直线上与点point不相同的点的数量。
- 使用 Counter 来统计斜率出现的次数。
- 使用 same、diff 和 max_points 来更新 max_points，用于保存历史中同一直线上最多的点数。
- 最后返回 max_points 即可。
from collections import Counter
class Solution:
def maxPoints(self, points: List[List[int]]) -> int:
# 当点少于3个，则必定能构成直线，直接返回即可
if len(points) < 3:
return len(points)
# 求斜率，注意分母为0的情况
def slope(point1, point2):
return float('Inf') if point1[1] - point2[1] == 0 else (point1[0] - point2[0]) * 1000 / (point1[1] - point2[1]) * 1000
max_points = 0 # 记录同一直线上最多的点数
# 遍历每个点
for point in points:
# 记录与点point相同的点的数量
same = sum(1 for other_point in points if point == other_point)
# 计算point与其他不相同的点的斜率，并统计斜率的出现次数
count = Counter([slope(point, other_point) for other_point in points if point != other_point])
# 记录同一直线上与点point不相同的点的数量
diff = count.most_common(1)[0][1] if count else 0
# same + diff表示当前point点所在直线上最多的点
# 更新max_points
max_points = max(same + diff, max_points)
return max_points复杂度分析：
- 时间复杂度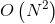：，其中 N 是
points的长度。我们需要使用两重循环来计算任意两点之间的斜率。 - 空间复杂度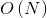：，用来记录最多不超过 N-1 条直线的斜率。
219. 存在重复元素 II
难度 简单
题目：给定一个整数数组和一个整数 k，判断数组中是否存在两个不同的索引 i 和 j，使得 nums [i] = nums [j]，并且 i 和 j 的差的 绝对值 至多为 k。
思路：
- 前提：题目所述等价于判断 nums[i] 的滑动窗口 nums[i-k: i] + nums[i+1: i+k] 内是否存在 nums [j] 使得 nums [i] = nums [j]。
- 首先初始化 s 来维持 k 大小的滑动窗口。
- 然后遍历 nums，若 nums[i] 在滑动窗口 s 内，则可以直接返回 True；若 nums[i] 不在滑动窗口 s 内，则将元素 nums[i] 添加至滑动窗口 s。
- 若滑动窗口 s 的大小超过 k，则移除最先添加的元素，维持窗口大小为 k。
- 最后遍历完没有找到符号条件的元素，则返回 False。
class Solution:
def containsNearbyDuplicate(self, nums: List[int], k: int) -> bool:
s = set() # 用于维持k大小的滑动窗口
# 遍历nums
for i in range(len(nums)):
# 若当前元素存在于滑动窗口内，则直接返回
if nums[i] in s:
return True
# 将当前元素添加到集合s
s.add(nums[i])
# 若滑动窗口的大小超过k，则移除最先添加的元素，维持窗口的大小为k
if len(s) > k:
s.remove(nums[i-k])
return False复杂度分析：
- 时间复杂度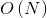：，其中 N 是
nums的长度。我们执行了一重循环来遍历 nums。 - 空间复杂度：
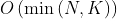，用来记录滑动窗口的集合 s 的大小。
220. 存在重复元素 III
难度 中等
题目：在整数数组 nums 中，是否存在两个下标 i 和 j，使得 nums [i] 和 nums [j] 的差的绝对值小于等于 t ，且满足 i 和 j 的差的绝对值也小于等于 ķ 。
如果存在则返回 true，不存在返回 false。
思路：
- 前提：
- 题目所述等价于判断 nums[j] 是否在 nums [i] 的区间 [nums[i]-t, nums[i]+t] 内，同时要保证 j 在区间 [i-k, i+k] 内。
- 采用分桶的思想，定义大小为 t+1 的桶，其中每个桶存储一个元素，若一个桶中存在 2 个元素，那么表示这 2 个元素足够接近，符合条件，直接返回即可。
- 首先定义一个字典 d 来存储桶号与对应元素。
- 然后遍历数组，计算出 nums[i] 对应的桶号，若桶号在 d 中已经存在，则直接返回；若 nums[i] 与前一个桶中的元素的差的绝对值小于等于 t ，则返回；若 nums[i] 与后一个桶中的元素的差的绝对值小于等于 t ，则返回。
- 若桶号不在 d 中，则将其添加进去。
- 注意：要通过移除“过期”的元素来维持大小为 k 的滑动窗口。
- 最后如果遍历完成没有找到符合条件的元素，则返回 False。
class Solution:
def containsNearbyAlmostDuplicate(self, nums: List[int], k: int, t: int) -> bool:
# 两数之差的绝对值肯定不会小于0
if t < 0:
return False
d = dict() # 保存桶号-元素对
for i in range(len(nums)):
idx = nums[i] // (t + 1) # 计算nums[i]的桶号，其中t+1表示桶的大小
if idx in d:
# 若idx号桶已经存在元素，表示桶内元素与nums[i]的差的绝对值肯定小于等于t
return True
elif idx - 1 in d and abs(nums[i] - d[idx-1]) <= t:
# 若idx-1号桶内的元素与nums[i]的差的绝对值小于等于t，则返回True
return True
elif idx + 1 in d and abs(nums[i] - d[idx+1]) <= t:
# 若idx+1号桶内的元素与nums[i]的差的绝对值小于等于t，则返回True
return True
d[idx] = nums[i] # 将nums[i]添加至idx号桶
if i >= k:
# 维持大小为k的滑动窗口
d.pop(nums[i-k] // (t + 1))
return False复杂度分析：
- 时间复杂度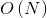：，其中 N 是
nums的长度。对于这 N 个元素中的任意一个元素来说，我们最多只需要对字典进行三次搜索，一次插入和一次删除即可，而这些操作是常量时间复杂度的。 - 空间复杂度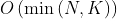：，用来记录滑动窗口的字典 d 的大小。
447. 回旋镖的数量
难度 简单
题目：给定平面上 n 对不同的点，“回旋镖” 是由点表示的元组 (i, j, k) ，其中 i 和 j 之间的距离和 i 和 k 之间的距离相等（需要考虑元组的顺序）。
找到所有回旋镖的数量。你可以假设 n 最大为 500，所有点的坐标在闭区间 [-10000, 10000] 中。
思路：
- 前提：
- 使用字典存储两点之间距离出现的次数，然后根据排列组合的知识将结果进行累加。
- 当一个距离出现的次数为 v 时，表示有 v 对点可以组合出回旋镖，因此有
种组合方式。又因为题目要求考虑顺序，所以最终的组合数为
。
- 首先初始化字典，用于统计距离出现的次数。
- 然后使用二重循环遍历所有点，并计算两点之间的距离，同时记录距离的出现次数。
- 最后将所有能够构成回旋镖的组合进行累加即可。
from collections import defaultdict
class Solution:
def numberOfBoomerangs(self, points: List[List[int]]) -> int:
# 计算两点之间的距离，此处省略了根号运算（省略后对结果没有什么影响）
def distance(x, y):
return (x[0] - y[0]) ** 2 + (x[1] - y[1]) ** 2
d = defaultdict(int) # 统计距离出现的次数
res = 0 # 用于将所有可能的情况累加起来
for i in points:
d.clear() # 清空字典
for j in points:
# 若遍历到同一个点，则跳过
if i == j:
continue
d[distance(i, j)] += 1 # 计算距离，并将其添加到字典中
# 遍历字典的值，累加结果
for v in d.values():
if v > 1: # 距离的出现次数大于1才有可能构成回旋镖
res += v * (v - 1)
return res # 返回累加结果复杂度分析：
- 时间复杂度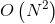：，其中 N 是
points的长度。我们需要二重循环来计算两点之间的距离。 - 空间复杂度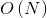：，用来统计距离的次数的字典 d 的大小。
454. 四数相加 II
难度 中等
题目：给定四个包含整数的数组列表 A , B , C , D ,计算有多少个元组 (i, j, k, l) ，使得 A[i] + B[j] + C[k] + D[l] = 0。
为了使问题简单化，所有的 A, B, C, D 具有相同的长度 N，且 0 ≤ N ≤ 500 。所有整数的范围在
到
之间，最终结果不会超过
。
思路：
- 前提：A[i] + B[j] + C[k] + D[l] = 0 可以转换为 A[i] + B[j] = - C[k] - D[l]。
- 首先遍历 A 和 B 数组，统计两两元素之和 A[i] + B[j]，以及出现的次数。
- 然后遍历 C 和 D 数组，将两两元素之和 - C[k] - D[l] 所对应的次数进行累加。
- 最后返回累加结果即可。
from collections import Counter
class Solution:
def fourSumCount(self, A: List[int], B: List[int], C: List[int], D: List[int]) -> int:
# 统计A、B中两两元素之和出现的次数
count = Counter(a+b for a in A for b in B)
# 将使等式A[i] + B[j] + C[k] + D[l] = 0成立的结果进行累加
return sum(count[-c-d] for c in C for d in D)复杂度分析：
- 时间复杂度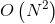：，其中 N 是数组的长度。我们需要两个二重循环来统计两两元素之和，及其出现的次数，即
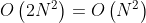。 - 空间复杂度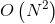：，用来统计两数之和出现的次数的字典 count 的大小。