Java学习第二十八天
目录
递归
递归运用案例1:
递归运用案例2:
递归运用案例3:
由以上案例总结出的递归规则
练习
第一题
第二题
递归
从方法中调用方法本身,每次调用传入不同的变量
解决问题的案例:汉诺塔,八皇后,老鼠出迷宫
递归运用案例1:
代码:
public class Recursion01{
//编写一个main方法
public static void main(String[] args){
T t1 = new T();
t1.test(4);
}
}
class T{
public void test(int n){
if(n > 2){
test(n - 1);//不断的开辟新的方法空间,知道n>2不成立为止
}
System.out.println("n=" + n);//当n=2时输出n=2;
}
}
编译之后的运行结果:
内存分析图:
基本原理:每一个栈都是独立的空间,运行完方法所在的栈之后会返回上一级的栈空间继续执行剩余的代码
递归运用案例2:
将上述代码稍作改动
public class Recursion02{
//编写一个main方法
public static void main(String[] args){
T t1 = new T();
t1.test(4);
}
}
class T{
public void test(int n){
if(n > 2){
test(n - 1);//不断的开辟新的方法空间,直到n>2不成立为止
}else{
System.out.println("n=" + n);//当n=2时输出n=2;
}
}
}
编译运行结果
分析:进入到if语句中时就不会再执行else中的语句了
递归运用案例3:
阶乘
代码:
public class Recursion03{
//编写一个main方法
public static void main(String[] args){
T t1 = new T();
int res = t1.factorial(5);
System.out.println("res=" + res);
}
}
class T{
//阶乘
public int factorial(int n){
if(n == 1){
return 1;
}else{
return factorial(n -1) * n;
}
}
}
编译运行结果
内存分析图
由以上案例总结出的递归规则
1.执行一个方法,就创建一个新的受保护的独立空间(栈空间)
2.方法的局部变量是独立的,互相之间不会影响
练习
第一题
斐波那契数列
代码
public class RecursionExercise01{
//编写一个main方法
public static void main(String[] args){
T t1 = new T();
int res = t1.fibo(5);
System.out.println("res=" + res);
}
}
class T{
//斐波那契数列
//返回数据类型 int
//方法名 fibo
//形参(int n)
public int fibo(int n){
if(n >= 1){
if(n ==1 || n == 2){
return 1;
}else{
return fibo(n-1) + fibo(n-2);
}
}else{
System.out.println("请输入大于1的整数");
}
}
}
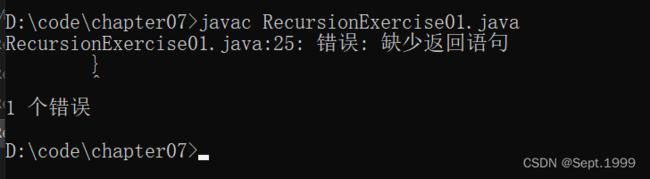
编译提示
原因分析:没有返回语句
困惑:不知道该怎么加
老师的解决思路:return -1;
public class RecursionExercise01{
//编写一个main方法
public static void main(String[] args){
T t1 = new T();
int res = t1.fibo(34);
System.out.println("res=" + res);
}
}
class T{
//斐波那契数列,1,1,2,3,5,8,。。。;
//要求:求出第n个数字的斐波那契数
//分析:f(1)=1;f(2)=1;f(3)=(f2)+f(1);f(4)=(f3)+f(2)
//返回数据类型int
//方法名:fibo
//形参(int n)
//方法体:分两种情况求斐波那契数
public int fibo(int n){
if(n >= 1){
if(n == 1 || n == 2){
return 1;
}else{
return fibo(n-1) + fibo(n-2);
}
}else{
System.out.println("请输入大于等于1的整数");
return -1;
}
}
}
最后代码
public class RecursionExercise01{
//编写一个main方法
public static void main(String[] args){
T t1 = new T();
int n = 0;
int res = t1.fibo(n);
if(res != -1){
System.out.println("当n=" + n + "时对应的斐波那契数是" + res);
}
}
}
class T{
//斐波那契数列,1,1,2,3,5,8,。。。;
//要求:求出第n个数字的斐波那契数
//分析:f(1)=1;f(2)=1;f(3)=(f2)+f(1);f(4)=(f3)+f(2)
//返回数据类型int
//方法名:fibo
//形参(int n)
//方法体:分两种情况求斐波那契数
public int fibo(int n){
if(n >= 1){
if(n == 1 || n == 2){
return 1;
}else{
return fibo(n-1) + fibo(n-2);
}
}else{
System.out.println("请输入大于等于1的整数");
return -1;
}
}
}
res != -1;即满足n>=1这个条件;
如果n<1时,res = -1;输出“请输入大于等于1的整数”
第二题
猴子吃桃
问题描述:猴子吃桃,第一天吃了总数的一半多一个,第二天吃了剩下的一半多一个,第三天吃了第二天剩下的一半多一个,以此类推,第10天还剩一个(还没吃),求第一天没吃之前有多少个桃子?
逆序推导:总结规律(重要)
day10=1;
day9=(day10+1)*2
day8=(day9+1)*2
....
day n=(day(n+1)+1)*2
代码:
public class RecursionExercise02{
public static void main(String[] args){
T t1 = new T();
int day = 9;
int peachNum = t1.peach(day);
if(peachNum != -1){
System.out.println("第" + day + "天有" + peachNum + "个桃子");
}
}
}
class T{
//猴子吃桃,第一天吃了总数的一半多一个,第二天吃了剩下的一半多一个,
//第三天吃了第二天剩下的一半多一个,以此类推,第10天还剩一个(还没吃),求有多少个桃子
/*
思路分析:逆向推理
day10=1;
day9=(day10+1)*2
day9=(day8+1)*2
....
day n=(day(n+1)+1)*2
*/
//返回数据类型:int
//方法名peach
//形参(int day)
//方法体:分三种情况计算桃子数
public int peach(int day){
if(day == 10){
return 1;
}else if(day >= 1 && day <= 9){
return (peach(day+1) + 1) * 2;//重要的是找到规律
}else{
System.out.println("请输入1-10之间的整数");
return -1;
}
}
}