【Python算法系列十】二分查找算法
二分查找，也叫折半查找，是一种适用于顺序存储结构的查找方法。它是一种效率较高的查找方法，时间复杂度为 O(lgn)，但它仅能用于有序表中。也就是说，表中的元素需按关键字大小有序排列。
二分查找用左右两个指针来标注查找范围。程序开始时，查找范围是整个线性表，左指针指向第一个元素，右指针指向最后一个元素；每一次循环过后，查找范围都缩小为原先的一半，直到左右指针重叠或者左指针处于右指针的右侧。因为每次缩小一半的范围，所以可以得出二分查找的时间复杂度为 O(lgn)。
我们以图 1 中的有序数组为例进行二分查找。格子中的数是数组的每个位置上存储的数据，格子下方的数是下标。
图 1：有序数组
我们以 31 为关键字，在数组中进行二分查找，来找出关键字出现时的下标。
- 首先，如图 2 所示，初始化左右指针。左指针存储着第一个元素的下标，右指针存储着最后一个元素的下标。此时查找的范围是整个数组。
图 2：初始化二分查找
-
随后，求出左右指针的平均值 mid=7，如图 3 所示。由于数组有序，mid 指向的元素必定大于等于左指针指向的数，小于等于右指针所指向的数。将 mid 指向的元素与关键字 31 比较，发现 23 小于 31。
图 3：求出 mid -
因为 23 小于 31，又因为数组有序，可以得出下标小于等于 7 的数皆小于关键字。此时，把左指针 left 赋值为 mid+1，缩小搜索范围，去掉已知小于关键字的部分，把查找范围缩小到下标 8～15，如图 4 所示。
图 4：移动左指针 -
类似地，再次求出左右指针的平均值 mid。此时 mid=11，mid 指向的元素为 40。40 大于关键字 31，如图 5 所示。
图 5：求出 mid -
因为 mid 指向的元素 40 大于关键字，又因为数组有序，可以得出下标大于等于 11 的元素皆大于关键字。此时，把右指针 right 赋值为 mid-1，把查找范围缩小至下标 8～10，缩小搜索范围，去掉已知大于关键字的部分，如图 6 所示。
图 6：移动右指针 -
重复求平均值的步骤。此时，发现 mid 指向的元素等于关键字，如图 7 所示。输出 mid，即为关键字在数组中的下标。
图 7：二分查找完成
以上是当数据存在于数组中的二分查找全过程。如果数据并不存在于数组中，左右指针会重叠甚至过界，这时候就需要循环条件来作判断。
我们以 16 作为关键字，在相同的有序数组中做二分查找来演示关键字不存在于数组中的情况。
-
如图 8 所示，初始化左右指针，指向头尾元素。
图 8：初始化左右指针 -
求出左右指针的平均值 mid=7，如图 9 所示。mid 指向的元素 23 大于关键字 16。
图 9：求出 mid 指针 -
已知 mid 指向的元素小于关键字（见图 10 ），把右指针赋值为 mid-1，把搜索范围缩小到下标 0～6，缩小搜索范围，去掉已知大于关键字的部分。
图 10：为右指针赋值 -
如图 11 所示，再次求出左右指针的平均值 mid=3。mid 指向的元素 8 小于关键字 16。
图 11：重复相似步骤 -
已知 mid 指向的元素大于关键字（见图 12），把左指针赋值为 mid+1，把搜索范围缩小到下标 4～6，缩小搜索范围，去掉已知小于关键字的部分。
图 12：给左指针赋值 -
如图 13 所示，再次求出左右指针的平均值 mid=5。mid 指向的元素 15 小于关键字 16。
图 13：重复相似步骤 -
把左指针赋值为 mid+1=6，此时左右指针重叠，如图 14 所示。
图 14：左右指针重叠 -
再次求出左右指针的平均值 mid。此时，mid 指向 17（见图 15），17 大于关键字 16。
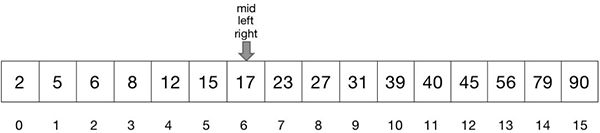
图 15：三个指针重叠 -
如图 16 所示，由于 mid 指向的元素大于关键字，把右指针赋值为 mid-1。此时左指针已处于右指针的右侧，说明数组中不存在含有关键字的查找范围。换而言之，关键字并不存在于数组中。二分查找结束，输出 -1。
图 16：二分查找完成
下面是二分查找的代码实现：
arr = [2,5,6,8,12,15,17,23,27,31,39,40,45,56,79,90]
l,r = 0,len(arr)-1 #初始化左右指针
n = int(input()) #输入关键字
while l <= r: #循环条件，判断是否存在合理的查找范围
mid = (l+r)//2 #求出左右指针的平均数
if arr[mid] < n: #折半缩小查找范围
l = mid+1
elif arr[mid] > n:
r = mid-1
else: #如果mid指向的元素与关键字相等，直接输出下标并跳出循环
print(mid)
break
#while循环自然结束，说明没有查找到与关键字相等的元素
print(-1)
运行程序，输入 8 时，输出结果为 3；输入 20 时，输出结果为 -1。
程序中，为了保证 mid 存储的数据是 int 类型（列表的下标必须是整数），使用//来对左右指针取平均数。同时，因为列表是有序的，所以当 mid 指向的元素大于关键字时，可以直接得出 mid 以及下标大于 mid 的元素组成的集合中必定没有关键字存在。
此时可以直接把这一侧的元素排除出查找范围；由于右指针指向查找范围的上限，此时右指针指向 mid-1。同理，当 mid 指向的元素小于关键字时，左指针指向 mid+1。
循环条件 l>=r 是为了保证当前的查找范围合法。当 l==r 时，查找范围内仅有一个元素。如果范围再次缩小（l>r 时），代表查找范围内已经没有元素或是有负数个元素。这明显处于不合法的状态，也说明列表中并不存在与关键字相等的元素。
在需要查找的结果不同时，二分查找也需要在细节方面进行改动。下面，我们仍对同一个列表做二分查找，但这次要找出在列表中不大于关键字的最大值。
图 17～图 22 中的过程以 38 作为关键字。
- 首先初始化左右指针并计算左右指针的平均值，如图 17 所示。此时，mid 指向的元素小于关键字 38。
图 17：初始化左右指针并计算 mid 指针
这次计算平均值的公式为mid=(l+r+1)//2，为了防止循环无法顺利结束，在取平均值前 +1 的具体理由会在算法结束时讲到。
- 如图 18 所示，由于 mid=8 时指向的 27 小于关键字，为左指针赋值 8。这是因为题目要求找出不大于关键字的最大值。
图 18：给左指针赋值
此时已知确定的不大于关键字的最大值为 27——列表中的元素有序排列，下标小于 8 的元素必定不大于关键字的最大值，因为它们已经小于已知的 27。而下标大于 27 的元素又无法保证不大于关键字。所以，缩小左指针标记的范围时，需要保留 mid 指向的元素。再次求出 mid=12，此时 mid 指向的元素大于关键字。
-
如图 19 所示，上一个 mid=12 指向的元素 45 大于关键字 38，此时给右指针赋值 mid-1。这是因为 mid 指向的元素已经确认不符合题目要求，所以可以把 mid 指向的元素直接排除出查找范围。
图 19：重复相似步骤
再次求出平均值 mid=10，此时 mid 指向的元素仍大于关键字。 -
由于下标为 10 的元素 39 大于关键字 38，把右指针赋值为 mid-1，如图 20 所示。
图 20：给右指针赋值 -
再次求出 mid。如图 21 所示，由mid=(l+r+1)//2可得，当左指针与右指针相邻时，mid 等于右指针。
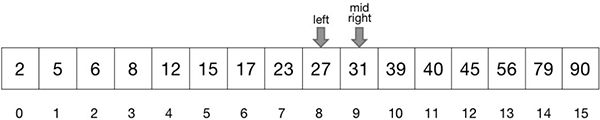
图 21：mid 指针与右指针重叠
此时，若 mid 指向的元素小于关键字，左指针会移动到 mid 的位置与右指针重叠；若 mid 指向的元素大于关键字，右指针会移动到 mid-1 的位置，同样与左指针重叠。
- 在当前列表中，mid 指向的元素小于关键字，所以左指针被赋值为 mid 并与右指针重叠，如图 22 所示。当左右指针重叠时，二分查找便结束了。查找到的答案就是左右指针同时指向的元素。
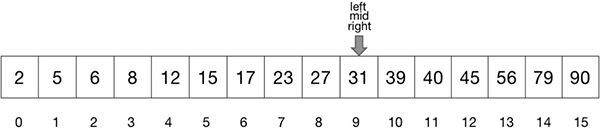
图 22：三个指针重叠
二分查找的代码实现：
arr = [2,5,6,8,12,15,17,23,27,31,39,40,45,56,79,90]
l,r = 0,len(arr)-1 #初始化左右指针
n = int(input())
while l < r: #仅当左右指针没有重叠时继续二分查找
mid = (l+r+1)//2 #求平均值
if arr[mid] <= n: #折半缩小查找范围
l = mid
else:
r = mid-1
print(l) #输出不大于关键字的最大元素下标
运行程序，输入 66 时，输出结果为 13；输入 3 时，输出结果为 0；输入 27 时，输出结果为 8。
与前一段程序相比，这一段二分查找的主要差别有 3 个：求平均值的方法不同、循环条件不同、折半缩小时处理 mid 的方法不同。
求平均值采用(l+r+1)//2是为了避免程序陷入死循环。当左右指针相邻时，若取平均值时使用 l+r， mid 的值将永远等同于 l 的值。而 l 的值必定小于等于关键字的值，所以 l 会被再次赋值为 mid，从而陷入死循环。在取平均值时+1 可以有效地解决这个问题。
循环条件不采用 l<=r，是因为当左右指针相等时，循环无法结束（同样，mid 等于 l，所以 l 不会 +1，永远小于等于 r）。并且，左右指针相等已经代表查找完成了。所以，使用 l 最后输出下标时，由于左右指针 l 和 r 相等，所以输出 l 或 r 是同样的效果。 二分查找是一种很实用也很常用的查找方法，它的代码编写较为简单，但需要注意适应不同要求时细节上的调整。只要数据有序排列，二分查找就能派上用场。一个常见的例子：在一段实数域中查找一个精确值。掌握二分查找是学习查找方法中必不可少的一环。