数据结构——栈和队列的实现（C语言版）

目录

一、栈（Stack）

1.什么是栈

2.栈的实现

①Stack.h

②Stack.c

③test.c

二、队列（Queue）

1.什么是队列

2.队列的实现

①Queue.h

②Queue.c

③test.c

---

一、栈（Stack）

1.什么是栈

栈是一种特殊的线性数据结构，其中的数据符合后进先出（Last In First Out）即LIFO的规则。

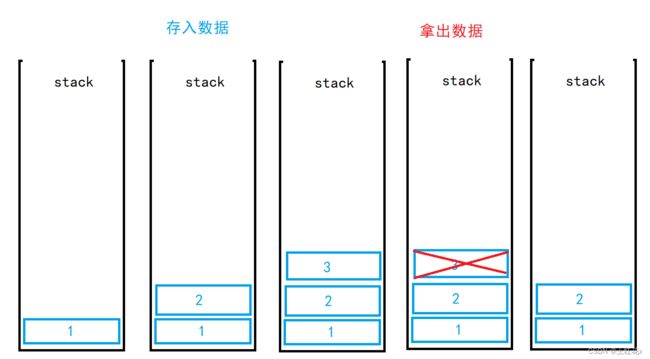
如图，栈就好比一个杯子，在存入数据的时候，我们肯定会先往杯子底部放东西，一件一件放，当我们要拿出东西的时候，也是从杯子顶部拿。

这个杯子我们成为栈，杯子的底部称为栈底，顶部称为栈顶，存入数据称为压栈，拿出数据称为出栈。上图中，我们先存入了 [1,2,3] 这三个数据，再出数据的时候，又拿出了 [3] ,剩下 [1,2] 。因为 [3] 是最后进去的，却是最先拿出来的，所以称为后进先出。这就是栈的特点。

2.栈的实现

要实现栈，我们就需要考虑一个问题，栈之间的数据怎么联系呢？是用顺序表的结构，还是链表的结构？

答案是两种都可以，但是我们这里采用顺序表的结构来实现，因为栈的插入和删除数据，相当于尾插和尾删，而链表在这一块效率显然没有顺序表高。

这里将栈的功能函数在头文件Stack.h中声明，这些函数的具体实现在Stack.c中，最后，我们在test.c中测试一下我们写的栈。（代码中有注释）

①Stack.h

#pragma once
#include 
#include 
#include 
#include 

// 因为不确定栈中存放的数据类型是什么，所以这里typedef一下
// 将来如果要用栈存 char，double或者是结构体，只要改动这里大部分问题就可以解决了
typedef int STDataType;

// 栈的空间可以动态增长
typedef struct Stack
{
	STDataType* a;
	int top;		// 栈顶
	int capacity;  // 容量 
}Stack;

// 初始化栈 
void StackInit(Stack* ps);
// 入栈 
void StackPush(Stack* ps, STDataType data);
// 出栈 
void StackPop(Stack* ps);
// 获取栈顶元素 
STDataType StackTop(Stack* ps);
// 获取栈中有效元素个数 
int StackSize(Stack* ps);
// 检测栈是否为空，如果为空返回非零结果，如果不为空返回0 
int StackEmpty(Stack* ps);
// 销毁栈 
void StackDestroy(Stack* ps);

②Stack.c

#include "Stack.h"
// 初始化栈 
void StackInit(Stack* ps)
{
	assert(ps);
    // 初始化栈时，将栈的容量和栈顶的位置置为0
	ps->a = NULL;
	ps->capacity = ps->top = 0;
}

// 入栈 
void StackPush(Stack* ps, STDataType data)
{
	assert(ps);
    // 当一个元素入栈时，我们要先检查一下栈是否为满
	if (ps->capacity == ps->top)
	{
    // 这里分两种情况讨论，如果是第一次，即栈的容量是0，就给一个初始容量，我这里给了4
    // 如果栈的容量不是0，就扩大为2倍
		ps->capacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		STDataType* temp = (STDataType*)realloc(ps->a, ps->capacity * sizeof(STDataType));
		if (temp == NULL)
		{
			perror("Increase Capacity Fail");
			exit(-1);
		}
		ps->a = temp;
	}
    // 之后将数据放到栈顶的位置
	ps->a[ps->top] = data;
    // 记得栈顶位置最后+1
	ps->top++;
}

// 出栈 
void StackPop(Stack* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));
    // 出栈操作十分简单，首先栈不能为空
    // 之后将栈顶的位置-1即可
	ps->top--;
}

// 获取栈顶元素 
STDataType StackTop(Stack* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));

	return ps->a[ps->top - 1];
}

// 获取栈中有效元素个数 
int StackSize(Stack* ps)
{
	assert(ps);

	return ps->top;
}

// 检测栈是否为空，如果为空返回非零结果，如果不为空返回0 
int StackEmpty(Stack* ps)
{
	assert(ps);
	if (ps->top == 0)
		return 1;
	return 0;

}

// 销毁栈 
void StackDestroy(Stack* ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
}

③test.c

#include "Stack.h"

void TestStack()；

int main()
{
	TestStack();
	return 0;
}

void TestStack()
{
    // 先创建一个栈st，之后初始化。
	Stack st;
	StackInit(&st);

    // 依次往栈里放入1-6，再看看栈的大小
	StackPush(&st, 1);
	StackPush(&st, 2);
	StackPush(&st, 3);
	StackPush(&st, 4);
	StackPush(&st, 5);
	StackPush(&st, 6);
	printf("%d\n", StackSize(&st));

    // 接着打印栈顶元素，然后移除栈顶元素，打印3个
	for (int i = 0; i < 3; ++i)
	{
		printf("%d ", StackTop(&st));
		StackPop(&st);
	}
	printf("\n");

    // 打印剩下所有的元素
	while (!StackEmpty(&st))
	{
		printf("%d ", StackTop(&st));
		StackPop(&st);
	}
	printf("\n");
    
    // 最后别忘了释放内存空间
	StackDestroy(&st);

}

二、队列（Queue）

1.什么是队列

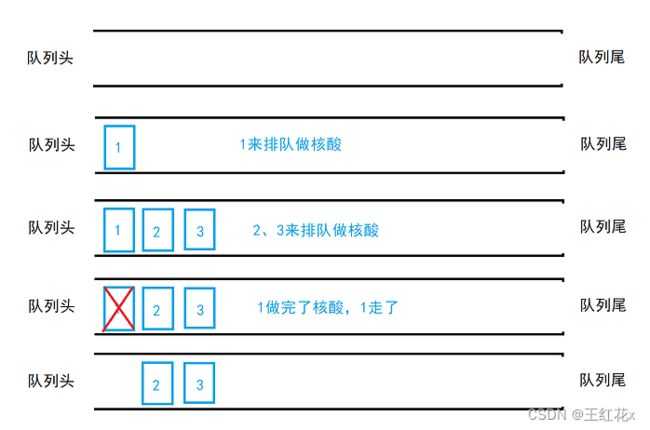
队列是另一种特殊的线性结构，上面我们讲过栈中的数据是后进先出（LIFO），而队列正好相反，是先进先出（FIFO）；

如图，队列就像它的名字一样，拍成一列，按顺序来排队，不准插队，排完就走。

2.队列的实现

在实现队列前，我们又要思考一下，队列中的数据是按顺序表的结构存储还是按链表的结构存储。两者当然都能实现队列，那么谁更方便或者效率更高呢？

这里我选择用链表实现。因为在队列出数据的时候，相当于头删，而顺序表每一次头删都要挪动n-1个数据。至于尾插，之后代码中有一个小妙招解决这个问题。

①Queue.h

#include 
#include 
#include 
#include 

typedef int QDataType;
// 链式结构：表示队列 
typedef struct QListNode
{
	struct QListNode* next;
	QDataType data;
}QNode;

// 队列的结构 
typedef struct Queue
{
    // front指针指向队列的头，rear指针指向队列的尾
	QNode* front;
	QNode* rear;
    // 队列中的数据个数
	int size;
}Queue;

// 初始化队列 
void QueueInit(Queue* q);
// 队尾入队列 
void QueuePush(Queue* q, QDataType data);
// 队头出队列 
void QueuePop(Queue* q);
// 获取队列头部元素 
QDataType QueueFront(Queue* q);
// 获取队列队尾元素 
QDataType QueueBack(Queue* q);
// 获取队列中有效元素个数 
int QueueSize(Queue* q);
// 检测队列是否为空，如果为空返回非零结果，如果非空返回0 
int QueueEmpty(Queue* q);
// 销毁队列 
void QueueDestroy(Queue* q);

②Queue.c

#include "Queue.h"

// 初始化队列 
void QueueInit(Queue* q)
{
	assert(q);
	q->front = NULL;
	q->rear = NULL;
	q->size = 0;
}

// 队尾入队列 
void QueuePush(Queue* q, QDataType data)
{
	assert(q);
	// 新建一个节点
	QNode* temp = (QNode*)malloc(sizeof(QNode));
	if (temp == NULL)
	{
		perror("Push Fail");
		exit(-1);
	}
	else
	{
		temp->data = data;
		temp->next = NULL;
	}
	// 队列为空尾插要另外标注
	if (QueueEmpty(q))
	{
		q->front = temp;
		q->rear = temp;
	}
    // 队列不为空时正常尾插
	else
	{
		q->rear->next = temp;
		q->rear = temp;
	}
	q->size++;
}

// 队头出队列 
void QueuePop(Queue* q)
{
	assert(q);
	assert(!QueueEmpty(q));
	
	QNode* del = q->front;
	q->front = q->front->next;
	free(del);

	q->size--;
    // 如果删空了，队尾也要置为空
	if (q->size == 0)
		q->rear = NULL;
}

// 获取队列头部元素 
QDataType QueueFront(Queue* q)
{
	assert(q);
	assert(!QueueEmpty(q));

	return q->front->data;
}

// 获取队列队尾元素 
QDataType QueueBack(Queue* q)
{
	assert(q);
	assert(!QueueEmpty(q));

	return q->rear->data;
}

// 获取队列中有效元素个数 
int QueueSize(Queue* q)
{
	assert(q);
	return q->size;
}

// 检测队列是否为空，如果为空返回非零结果，如果非空返回0 
int QueueEmpty(Queue* q)
{
	assert(q);
	if (q->size == 0)
		return 1;
	return 0;
}

// 销毁队列 
void QueueDestroy(Queue* q)
{
	assert(q);
	while (q->size)
	{
		QueuePop(q);
	}
}

③test.c

#include "Queue.h"

void TestQueue()；

int main()
{
	TestQueue();

	return 0;
}

void TestQueue()
{
    // 新建一个队列并初始化
	Queue q;
	QueueInit(&q);

    // 依次插入1 2 3，再看一下队列尾部元素（不删除）
	QueuePush(&q, 1);
	QueuePush(&q, 2);
	QueuePush(&q, 3);
	printf("%d\n", QueueBack(&q));

    // 再插入4 5 6
	QueuePush(&q, 4);
	QueuePush(&q, 5);
	QueuePush(&q, 6);
    
    // 打印队头数据，并删除队头数据
	while (!QueueEmpty(&q))
	{
		printf("%d ", QueueFront(&q));
		QueuePop(&q);
	}
	printf("\n");

	QueueDestroy(&q);
}