基础算法(四)——高精度
文章目录
-
- 高精度
-
- 介绍
-
- 核心思想:
- 模板代码:
- 例题1:
-
- 代码:
- 例题2:
-
- 代码:
- 例题3:
-
- 代码
- 例题4:
-
- 代码
高精度
介绍
高精度算法是用于处理大整数运算的,大整数的大小一般是,其位数len(x) <= 1e6,标准数据即x <= 1e9
一般来说考四种情况(大写字母代表大数据,小写字母代表标准范围数据):
- 大整数相加
A+B - 大整数相减
A-B - 大整数乘小整数
A*a - 大整数除小整数
A/a
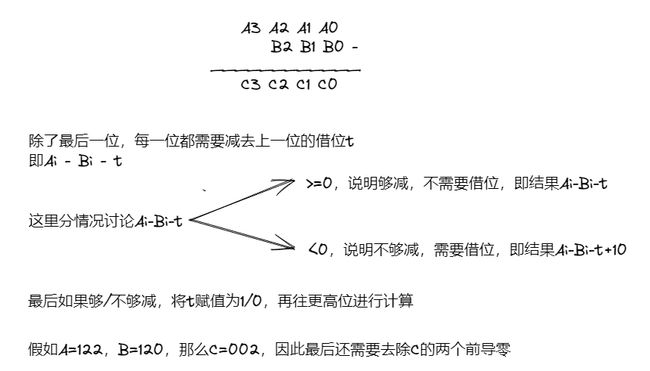
具体做法是:将大整数的每一位存放到数组里去,C++里一般先用字符串string将数据读入,然后将每一位存放到整形数组中。这里我们从数据的低位先进行存放,即假设数据x=123456789,那么数组a[0] = 9,方便后续进位操作,这样最后只需要在数组末端直接加一个数。然后结合进位和借位进行逐位运算。
高精度的思想很简单,但是代码需要好好理解一下,最好直接背
核心思想:
这里分四个情况讨论(以下大整数A的第i位都用A[i]表示):
模板代码:
高精度加法:
// C = A + B
vector add(vector A, vector B) // 返回A+B的值
{
int t = 0;
vector C;
for(int i=0; i 高精度减法:
// 判断A是否大于B
bool cmp(vector A, vector B)
{
if(A.size() != B.size()) return A.size() > B.size();
for(int i=A.size() - 1; i>=0 ; i++)
if(A[i] != B[i])
return A[i] > B[i];
return true;
}
// C = A - B
vector sub(vector A, vector B) // 返回A+B的值
{
vector C;
for(int i=0,t=0; i1 && C.back() == 0) C.pop_back();
return C;
}
// 主函数里的函数调用逻辑
int main()
{
if(cmp(A, B))
{
auto C = sub(A, B);
for(int i = C.size() - 1; i >= 0 ; i --) cout << C[i]; // 打印结果
}
else
{
auto C = sub(B, A);
cout << '-'; // 结果是负数,先输出一个负号
for(int i = C.size() - 1; i >= 0 ; i --) cout << C[i]; // 打印结果
}
}
高精度乘法:
vector mul(vector A, int b)
{
int t = 0;
vector C;
for(int i=0; i1 && C.back()==0) C.pop_back();
return C;
}
例题1:
代码:
#include
#include
using namespace std;
vector A, B;
vector add(vector A, vector B)
{
vector C;
int t = 0;
for(int i=0; i> a >> b;
for(int i=a.size()-1; i>=0; i--) A.push_back(a[i] - '0');
for(int i=b.size()-1; i>=0; i--) B.push_back(b[i] - '0');
auto C = add(A, B);
for(int i=C.size()-1; i>=0; i--) printf("%d", C[i]);
}
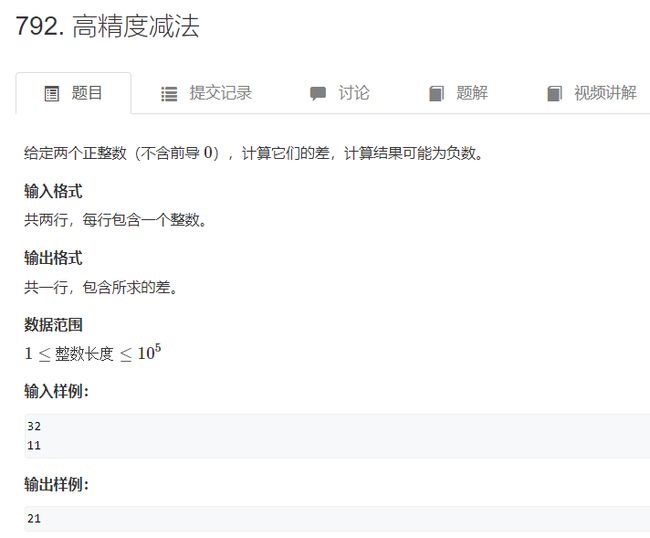
例题2:
代码:
#include
#include
using namespace std;
vector A, B;
// A >= B
bool cmp(vector &A, vector &B)
{
if(A.size() != B.size()) return A.size()>B.size();
for(int i=A.size()-1; i>=0; i--)
{
if(A[i]!=B[i]) return A[i] > B[i];
}
return true;
}
vector sub(vector &A, vector &B)
{
int t = 0;
vector C;
for(int i=0; i 1 && C.back() == 0) C.pop_back();
return C;
}
int main()
{
string a, b;
cin >> a >> b;
for(int i=a.size()-1; i>=0; i--) A.push_back(a[i]-'0');
for(int i=b.size()-1; i>=0; i--) B.push_back(b[i]-'0');
if(cmp(A, B))
{
auto C = sub(A, B);
for(int i=C.size()-1; i>=0; i--) printf("%d", C[i]);
}
else
{
auto C = sub(B, A);
printf("-");
for(int i=C.size()-1; i>=0; i--) printf("%d", C[i]);
}
}
例题3:
代码
#include
#include
using namespace std;
vector mul(vector A, int b)
{
int t = 0;
vector C;
for(int i=0; i1 && C.back()==0) C.pop_back();
return C;
}
int main()
{
string a;
int b;
cin >> a >> b;
vector A;
for(int i=a.size()-1; i >= 0; i--) A.push_back(a[i] - '0');
auto C = mul(A, b);
for(int i=C.size()-1; i >= 0; i--) printf("%d", C[i]);
return 0;
}
例题4:
代码
待整理