通过机器学习预测电网平均总负荷

0 概述

   该研究基于比利时Elia 电网公司的公开数据，该数据给出了过去几年以 15 分钟为间隔测量的 Elia 电网的总负荷。此处将使用机器学习方法提前一天预测平均总负荷。以上成果可用于实际的生产生活中，电力公司可以使用该预测值来产生足够的发电量，以避免电网中断和电力损失，并根据未来的负荷构建动态定价方案。

1 研究动机

   负荷预测对于输电运营商来说是一项至关重要的任务，电力系统的管理是一项复杂的任务，并且在很大程度上依赖于对未来电力需求的了解。可以准确预测负荷的模型对于能源生产至关重要，因为根据预测的负荷可以确定应该运行哪些设备以满足需求，更好地满足机组组合优化。若不能产生足够的能量会导致电网故障，若供过于求会导致能源和资源的浪费。
   负荷预测带来的一个经济效益是能够根据总需求对电力进行定价。能源市场的去中心化和激烈竞争使得输电运营商能够以具有竞争的价格来定价电力变得至关重要。 这些价格会随着电力需求而波动，高峰期的特点是电价高，非高峰期的价格也较低。 动态确定这些时间段何时发生以及这些时间段内的电力需求可以帮助制定基于需求的具有竞争力和公平性的定价方案。
   过去，人们采用各种预测方法来预测未来负荷，包括计量经济学方法、基于回归的模型和统计学习算法。这些方法取得了不同程度的成功，但仍有很大的改进空间。 我们的目标是将机器学习算法应用于负荷预测问题。此外，我们将使用时间序列分析方法对数据集进行缩放和去趋势化，为学习算法做好准备。

2 相关工作

   Taylor 等人在（[1]）中发现电力负荷时间序列中存在季节性模式，我们的研究将对 Elia 数据集中的季节性模式进行统计分析，并将该信息用于其中一种机器学习方法，研究证明该机器学习方法可以减少预测误差。
   Chen等人在（[2]）中也采用了一种机器学习方法来预测未来负荷，它使用支持向量机（SVM）来预测未来的电力负荷。 通过从过去几天的需求中形成特征向量来合并时间序列信息，并使用它们来预测未来几天的负荷。 在我们的研究中，将像本研究一样使用SVM进行预测，但将从日内电力负荷而不是从多天数据中构建特征向量。
   最后，研究中也包含了有 Ahmed 在 ([3]) 中的工作，它凭经验证明了在应用机器学习算法进行预测之前进行统计预处理时间序列数据的好处。 证明了数据归一化、对数缩放、趋势去除可以提高判别学习算法的性能， 在我们的方法中，我们将在应用机器学习方法之前对数据进行对数缩放并去除趋势分量，并将季节性信息用于基于聚类的学习算法。

3 统计学处理

   首先介绍一些将在整篇文章中使用的符号：
   xTrain - 按时间顺序组成 2008-2016 年的负荷时间序列。 每个向量都是 96 维的，因为每十五分钟测量一次电网上的总负荷。
   yTrain - xTrain 中样本对应的第二天平均总负荷。平均总负荷是指第二天所有 96 个负荷值的平均值。
   xTest , yTest - 除 2017 年外，其他的与训练数据集相同。
   训练和测试集中的最后一个样本需要提取下一年的负荷值，这是作为预处理的一部分完成的。 我们在图 1 中绘制了相应时间段内的 yTrain 值。从图中可以看出，除了负荷的大数值外，似乎还有显着的趋势和季节性分量。 以下预处理步骤将解决这些问题，使数据更易于学习。
                  图 1 2008-2017 平均总负荷图

3.1 数据预处理

预处理阶段有 2 个步骤：
（1）对数缩放
   时间序列包含非常大的数值，这会阻碍学习器有效学习的能力并使问题计算密集。为解决以上问题，在学习之前，xTrain、yTrain 和 xTest 中的值将通过自然对数进行缩放。
（2）趋势消除
   消除目标值中的趋势可以提高预测准确度。 为此，我们首先通过对 yTrain 数据集执行最小二乘线性回归来估计趋势。将 yTrain 中的值视为按时间顺序排列的值序列。回归的自变量是从序列开始算起的天数，因变量是该特定日期的 yTrain 值。一旦计算出回归线，我们从 yTrain 中的每个值中减去回归预测值，从而获得去趋势的时间序列。xTrain值不受影响。

3.2 季节性分析

    根据之前的研究和观察，图 1 中 yTrain 的图，我们认为时间序列包含显着的季节性成分。为了验证该猜想，我们继续对季节性行为进行统计测试。
   首先，我们在图 2 中显示 yTrain 的滞后相关图，其中绘制了 yTrain 的值与其前一天的值。 这张图使我们能够确定基础时间序列是否是随机的。如果它是随机的，那么滞后图不应显示任何模式或有意义的子结构。 然而，根据该图，我们可以观察到一个显着的线性趋势，这表明可能是由季节性引起的某些潜在的模式。
   现在我们有了季节性成分的证据，我们将使用相关图（图3）来确定季节的周期。相关图根据时间滞后绘制自相关因子，其中自相关因子是在某个给定时间滞后下 yTrain 与自身的协方差除以 yTrain 的方差。 在数学上，对于时间滞后为 k 的 yTrain 自相关因子rk 的估计可以表示为：

   我们让 n = |yTrain| ， 假设值 yTrain 是独立同分布的。 自相关因子的均值和方差分别为 -1/n 和 1/n 。 这些可用于查找 95% 和 99% 置信区间，它们在相关图上显示为水平线。
   从相关图中我们可以观察到，2008 - 2016 年图上的滞后一年和 2016 年图上的滞后一周都产生超过 99% 置信区间的自相关因子。 此外，我们构建了周期图（图4），可用于识别频域中时间序列的重要周期。 通过检查周期图，我们观察到每周和每年频率的峰值，这表明这些时间滞后的时间序列有很强的相关性。 根据这些统计检验的结果，我们可以得出结论，时间序列很可能包含显着的季节性成分。 我们将使用每周和每年作为基于聚类的机器学习算法的季节性周期，这将在下一节中描述。

4 算法

   主要利用四种机器学习算法进行学习，包括聚类、支持向量回归、神经网络和高斯过程回归。
   除此之外，我们还尝试了其他机器学习算法来探索其在电力负荷预测上的能力，如逻辑回归、决策树、随机森林、XGboost机器学习算法，以及长短时记忆网络、门控递归单元神经网络等深度学习算法。该部分内容不作为研究的主要内容，后续可进行持续探索。

4.1 支持向量回归SVR

   第一个基于机器学习的预测方法使用支持向量机回归 (SVR)。 传统上支持向量机用于二元分类任务，并在高维度上找到欧几里得空间中的最佳超平面，将数据分为两类。 该算法已经针对回归任务进行了修改，因此我们可以将其应用于当前的问题。我们使用核函数 k 代替其对偶公式中的内积项，k度量了高维向量空间中的内积的相似性，并允许 SVR 学习关于原始向量空间的非线性模式。
基于 SVR 算法的预测步骤：
   算法输入：核函数 k 和误分类惩罚系数 C 以及训练和测试数据集。
   数据预处理：将缩放和去趋势步骤应用于 xTrain 和 yTrain，如预处理部分所述，以获得实际训练集。
   模型训练：然后将 SVR 与内核 k 和惩罚 C 与 训练集一起使用以获得预测器 f。
   预测：对于每个样本 x ∈ xTest，算法对进行缩放并应用 f 以获得其对应的预测值。 然后将趋势分量加回到该预测值上，通过逆自然对数重新缩放以获得最终预测值。

4.2 聚类Clustering

   第二个机器学习方法是聚类，并使用预处理部分中检验过的季节性信息。 我们将季节长度视为样本的唯一类别的数量。集群个数k：聚类的集群个数使用了季节性分析得到的周期，具体就是将季节长度视为集群个数k，如周期为周，那么集群数目k=7,周期为年，那么k=365。
   两种不同的聚类算法： 第一种是自底向上的凝聚法层次聚类，距离采用离差平方和法(ward)计算，目的是最大化集群间的距离，以最小化集群内的总方差为目标合并集群。 第二种聚类方法是 K-Means聚类，它使用欧几里德距离度量将一组向量聚类到 k 个集群中中，目标是最小化集群内平方和。
基于聚类算法的预测步骤：
   算法输入：包括季节长度 s（有7和365，作为集群个数）、聚类算法的选择（K-Means 或ward凝聚层次聚类），以及训练和测试数据集。
   数据预处理：将缩放和去趋势步骤应用于 xTrain 和 yTrain，如预处理部分所述，以获得实际训练集。
   模型训练：在训练集上运行聚类簇数为s 的两种聚类算法，以获得一组集群及其对应的质心。
   预测：对于测试集中的样本，找到与样本欧式距离最小的质心对应的集群。然后利用加权聚类分类得到其预测值。（利用加权距离和/距离和，得到临时预测值。权值为当前样本所属集群中个体预测目标值，距离为它们各自和样本之间的欧式距离。最后对该临时预测值进行加趋势，逆标准化，得到原始量纲的预测值。）

4.3 神经网络Neural Networks

   第三种学习方法是神经网络， 有一组输入神经元接收一个样本并将样本向量的值输出到后续的隐层神经元。这些隐层神经元采用其输入的线性组合，可能会添加一个偏置值，然后将激活函数应用于该计算的总和，并将获得的值沿传出边输出到其他神经元。以这种方式，值从输入层通过网络传播，直到它们到达输出层，在输出层，误差函数被应用于输出层神经元的输出值。然后通过著名的反向传播算法更新网络，该算法尝试通过调整网络权重来最小化获得的误差。
   优化方法：我们使用的神经网络将使用随机梯度下降 (SGD) 进行训练，它从样本的子集而不是整个数据集估计梯度。以这种方式更新权重可以加快收敛速度。
   降维方法：我们将使用主成分分析 (PCA) 来降低特征向量的维数。这样做的原因是训练集包含大约 3000多个样本，由于参数数量的原因，这对于训练具有 96 个输入神经元的网络来说太少了。 因此，我们使用 PCA 将样本投影到较低维度的子空间中，同时保持最大的方差量，这会保留区分样本所需的信息，也减少了输入神经元的个数。
基于神经网络的预测步骤：
   算法输入：由训练和测试数据集、隐藏神经元数量的正整数 h 和 PCA 的维度 d 组成（激活函数 sigmoid和误差函数平方损失是固定的，并且有一个隐藏层）。
   数据预处理：首先对数缩放和去趋势 yTrain 以获得 Y’train 。对数缩放并将目标维度为 d 的 PCA 应用到 xTrain 以获得 X’ train，保留用于 PCA 的投影矩阵 W。
   模型训练：在训练集 X’ train上运行神经网络算法，得到训练好的学习器。
   预测：对于每个示例 x ∈ xTest，对 x 进行对数缩放以获得 x ˆ，然后通过使用公式 x0 = W ˆx 进行投影获得 x0。将神经网络应用于 x0 得到输出 y0 ，然后加入趋势分量并用逆自然对数重新缩放以获得预测值 y。

4.4 高斯过程回归 Gaussian Process Regression

   第四种学习方法将使用高斯过程回归 (GPR)，这是一种主要用于回归任务的判别学习算法。
GPR预测算法如下
   算法输入：由协方差函数 k 以及训练和测试数据集组成。
   数据预处理：对 xTrain 和 yTrain 应用对数缩放和去趋势操作。
   模型训练：然后在训练集上使用 GPR，得到 预测器 f。
   预测： 然后对于每个样本 x ∈ xTest 应用对数归一化以获得 x0， 并计算 y0 = f(x0)。 然后将趋势分量加回到 y0 并应用逆自然对数以获得预测 y。

5 实施

   该项目是用 Python 实现的，大量使用了 scikit-learn机器学习库、Numpy 数值计算库、Pandas 数据分析库、Pybrain 机器学习库、keras深度学习库。 系统架构如下：
   • Win10家庭版64位操作系统
   • CPU处理器（Intel®Core™i5-6200U）
   • 8GB 内存

6 实验结果

   将四种基于机器学习的算法与计量经济学模型一起应用于预测 2017 年平均总负荷的任务中。对于每种算法，我们尝试了几种不同的参数，并在单个图上显示每种配置的结果。 图 5、6、7、8 分别显示了SVR、聚类、GPR 和神经网络结果。
   我们选择根据归一化均方根误差 (NRMSE) 来衡量性能，因为它是经过缩放的，并且允许在算法之间进行公平的比较。 如果让 Ypred 和 Ytest 分别为 n 个预测值和对应的测试值，则 NRMSE 的函数可以表示为：

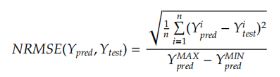
   我们测量了所有算法及其各种配置的 NRMSE，并在表 1 中显示了结果和参数选择。
   我们注意到，最低的 NRMSE值0.10558是通过 GPR 实现的。 GPR 超越聚类、SVR 和神经网络算法的事实证明了 GPR 在数据集不太大（例如，最多几千个示例和几十个维度）时在判别回归学习任务可实现高准确率。然而，除了预处理步骤之外，GPR 模型中没有使用有关季节性的信息。这表明季节性信息可能不是实现高准确率预测平均总负荷所必需的。但我们发现归一化和去趋势的预处理步骤对于机器学习方法的很重要，因此表明时间序列分析的思想与机器学习结合使用可以开发强大的预测模型。

7 未来方向

   基于我们的结果，我们有强有力的证据表明基于机器学习的算法能够实现负荷预测问题的高准确率，因此我们相信进一步探索这一领域将是有益的。
   一个直接的方向是尝试其他判别机器学习算法，如贝叶斯神经网络、k-最近邻、回归方法（岭、逻辑、贝叶斯）和决策树，并根据本文中的结果衡量它们的性能。
   由于我们的算法通常有很多参数（SVR 有核函数和误差惩罚，GPR 有协方差函数），另一个方向可能是尝试改变参数，看看另一个选择是否会产生更低的错误率。
此外，多种算法可以与集成方法一起使用，历史上已经证明在某些情况下它们优于集成的组成算法。
   此外，研究时间序列分析中的方法以及如何将它们与机器学习结合使用似乎也很有价值。 在这一点上，有多种时间序列方法可用于更改和转换数据集，从而可以更深入地了解和分析负责生成数据的底层过程。 一些方法包括了如噪声检测和去除、去季节性（尽管我们发现加法分解无效）和平滑（卡尔曼滤波、拉普拉斯算子）。 将这些技术与学习算法一起使用可能会产生强大而准确的预测器，这些预测器的性能可能优于使用纯计量经济学或机器学习方法。
   最后，将本文中使用的技术应用到从其他电力公司处收集其他电力负荷时间序列数据应用会很有用。我们认为，电力负荷时间序列具有某些共同点，例如季节性影响和趋势，并且本文中提出的预测方法至少会在此类数据集上取得一定程度的成功。天气数据也可以被收集并用于预测，其他研究人员已经证明这与电力使用密切相关。可以将获得的结果都可以与电力公司使用的结果进行比较，看看它们是否比工业中使用的结果更准确。还可以与现实世界的标准方法进行比较，以确定电力公司目前使用的预测方法是否可以改进。

8 结论

   根据我们的经验结果，我们已经成功地证明了机器学习技术可以产生准确的预测器，用于提前一天预测 Elia 电网的平均总负荷。但季节性信息并没有帮助提高使用高斯过程回归的最准确分类器的性能，尽管季节性信息是基于聚类的方法的组成部分，也实现了相当低的错误率。然而，我们发现对数缩放和去趋势的负荷时间序列显着提高了模型的准确性。总的来说，我们相信我们的方法清楚地证明了利用时间序列和机器学习方法的价值，我们推测这将是未来负荷预测工作中不可或缺的一部分。该问题仍然是一个活跃的研究领域，远未解决，希望电力运营商继续寻求改进的预测方法，因为负荷预测具有重要的实用价值。

参考文献

【1】James W Taylor, Lilian M De Menezes, and Patrick E McSharry. A comparison of univariate methods for forecasting electricity demand up to a day ahead. International Journal of Forecasting, 22(1):1–16, 2006. 3
【2】Bo-Juen Chen, Ming-Wei Chang, and Chih-Jen Lin. Load forecasting using support vector machines: A study on eunite competition 2001. Power Systems, IEEE Transactions on, 19(4):1821–1830, 2004. 3
【3】Nesreen K Ahmed, Amir F Atiya, Neamat El Gayar, and Hisham El-Shishiny. An empirical comparison of machine learning models for time series forecasting. Econometric Reviews, 29(5-6):594–621, 2010. 3