字典树讲解

题目描述：

给定 nn 个模式串 s1​, s2​, …, sn​ 和 q 次询问，每次询问给定一个文本串 ti​，请回答 s1​∼sn​ 中有多少个字符串 sj​ 满足 ti​ 是 sj​ 的前缀。

一个字符串 t 是 s 的前缀当且仅当从 s 的末尾删去若干个（可以为 0 个）连续的字符后与 t 相同。

输入的字符串大小敏感。例如，字符串 Fusu 和字符串 fusu 不同。

输入格式：

本题单测试点内有多组测试数据。

输入的第一行是一个整数，表示数据组数 T。

对于每组数据，格式如下：

第一行是两个整数，分别表示模式串的个数 n 和询问的个数 q。

接下来 n 行，每行一个字符串，表示一个模式串。

接下来 q 行，每行一个字符串，表示一次询问。

输出格式：

按照输入的顺序依次输出各测试数据的答案。

对于每次询问，输出一行一个整数表示答案。

分析：

该题若暴力求解，则一定会超时，故采用字典树进行求解。

字典树有以下特点：

1、根节点不包含字符，除根节点外每一个节点都只包含一个字符；

2、从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串；

3、每个节点的所有子节点包含的字符都不相同。

字符映射：

//因字符串中可能存在大写字母、小写字母、数字，故分开存放
//将大写字母放在最前面，小写字母放在中间，数字放在最后
int getnum(char x) {
    if(x >= 'A' && x <= 'Z')
        return x - 'A';
    else if(x >= 'a' && x <= 'z')
        return x - 'a' + 26;
    else
        return x - '0' + 52;
}

字符插入：

//trie[i][j]中i代表上个字符的节点编号，j为字符转换为数字的值
//trie[i][j]的值代表该字符的节点编号
void insert(string str) {
    int p = 0, len = str.length();
    for(int i = 0; i < len; ++i) {
        int ch = getnum(str[i]);
        //若trie[i][j]为零，则代表该节点还未建立，则需创建新节点
        //idx记录节点的编号
        if(!trie[p][ch])
            trie[p][ch] = ++idx;
        p = trie[p][ch];
        //cnt[i]记录从根节点至该节点字符串重复的次数
        cnt[p]++;
    }
}

字符串查询：

int find(string str) {
    int p = 0, len = str.length();
    for(int i = 0; i < len; ++i) {
        int ch = getnum(str[i]);
        //若编号为i的点不是一个单词的结束点，则该字符串不是前缀
        if(!trie[p][ch])
            return 0;
        //更新此时的上个字符的节点
        p = trie[p][ch];
    }
    //遍历结束，则输出此时得到的值
    return cnt[p];
}

完整代码：

#include 
using namespace std;
const int N = 3 * 1e6 + 10;
string s, t;
int T, n, q, idx, trie[N][100], cnt[N];

//因字符串中可能存在大写字母、小写字母、数字，故分开存放
//将大写字母放在最前面，小写字母放在中间，数字放在最后
int getnum(char x) {
    if(x >= 'A' && x <= 'Z')
        return x - 'A';
    else if(x >= 'a' && x <= 'z')
        return x - 'a' + 26;
    else
        return x - '0' + 52;
}

//trie[i][j]中i代表上个字符的节点编号，j为字符转换为数字的值
//trie[i][j]的值代表该字符的节点编号
void insert(string str) {
    int p = 0, len = str.length();
    for(int i = 0; i < len; ++i) {
        int ch = getnum(str[i]);
        //若trie[i][j]为零，则代表该节点还未建立，则需创建新节点
        //idx记录节点的编号
        if(!trie[p][ch])
            trie[p][ch] = ++idx;
        p = trie[p][ch];
        //cnt[i]记录从根节点至该节点字符串重复的次数
        cnt[p]++;
    }
}

int find(string str) {
    int p = 0, len = str.length();
    for(int i = 0; i < len; ++i) {
        int ch = getnum(str[i]);
        //若编号为i的点不是一个单词的结束点，则该字符串不是前缀
        if(!trie[p][ch])
            return 0;
        //更新此时的上个字符的节点
        p = trie[p][ch];
    }
    //遍历结束，则输出此时得到的值
    return cnt[p];
}

int main() {
    scanf("%d", &T);
    while(T--) {
        scanf("%d %d", &n, &q);
        //初始化
        //在第一次无需初始化
        //在后面的循环时，只需将已使用过的地方初始化即可，减少时间、空间开销
        for(int i = 0;i <= idx; i++) {
            cnt[i] = 0;
            for (int j = 0; j < 100; j++)
                trie[i][j] = 0;
        }
        idx = 0;
        while(n--) {
            cin >> s;
            insert(s);
        }
        while(q--) {
            cin >> t;
            printf("%d\n", find(t));
        }
    }
    return 0;
}

部分数据：

输入：
3
3 3
fusufusu
fusu
anguei
fusu
anguei
kkksc
5 2
fusu
Fusu
AFakeFusu
afakefusu
fusuisnotfake
Fusu
fusu
1 1
998244353
9

输出：
2
1
0
1
2
1

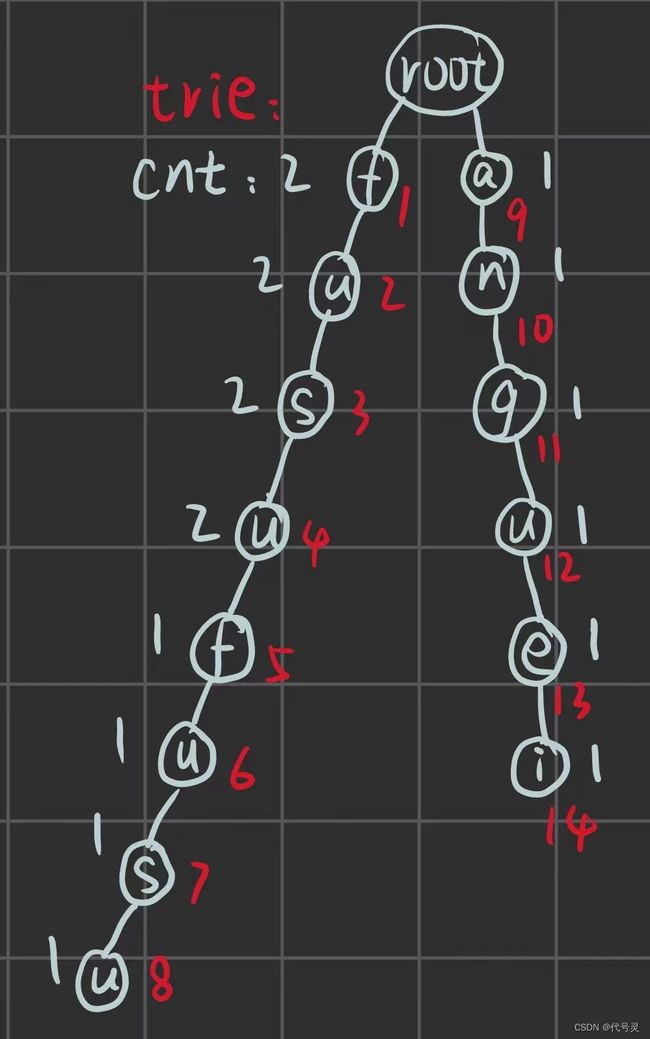
该数据中的第一个图可表示为：