PRML第十四章读书笔记——Combining Models 贝叶斯模型平均、委员会bagging、提升方法/AdaBoost、决策树、条件混合模型/混合线性回归/混合逻辑回归/【层次】混合专家模型
(终于读到最后一章了,吼吼!激动呀。我总感觉combining models已经有点频率派方法的味道了。所以接下来要读ESL?)
目录
- 14.1 Bayesian Model Averaging
- 14.2 Committees
- 14.3 Boosting
-
-
- P659 最小化指数误差
- P661 boosting的误差函数
-
- 14.4 Tree-based Models
- 14.5 Conditional Mixture Models
-
-
- P667 线性回归模型的混合
- P670 逻辑回归模型的混合
- P672 混合专家 mixtures of experts
- P673 层次混合专家 hierarchical mixture of experts (HME)
-
- *后记
- 委员会committe:训 L L L个不同的模型,然后取平均做预测
- 提升方法boosting:committee的变种,串行学一堆模型,依据之前模型的表现调整误差函数
- 决策树decision tree:如何把决策树看作是组合模型?从一堆模型中选一个,做决策,而不是平均。即对不同的输入区域用不同的模型
- 条件混合模型conditional mixture models:决策树是一种很硬的、平行于坐标轴的区域划分,可以采用一种概率模型去进行组合。例如有 K K K个模型,形式化为
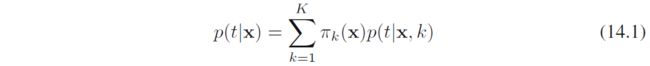
该混合概率分布的模型称为专家混合mixtures of experts. 该模型和5.6节的混合密度网络密切相关
14.1 Bayesian Model Averaging
贝叶斯模型平均和组合模型并不相同
组合模型如混合高斯,生成过程为

贝叶斯模型平均则是有几个不同的模型,索引为 h = 1 , … , H h=1,\dots,H h=1,…,H,并有概率 p ( h ) p(h) p(h)
(例如其中一个模型是混合高斯,一个模型是混合柯西分布等;再例如线性回归中参数先验分布,不同参数对应不同的模型)
数据集的生成过程为

贝叶斯模型平均实际上假设了只有一个模型用于生成整个数据, h h h上的概率仅仅是对于究竟是哪个模型在生成的不确定性。随着数据集规模增大,这个不确定性会减小,后验分布 p ( h ∣ X ) p(h|\bm X) p(h∣X)会集中到模型中的一个(例如线性回归的参数后验)
贝叶斯模型平均中,整个数据集由单一模型生成,相反,用组合模型时,数据集中的不同数据点可以由隐变量 z z z的不同值对应分量生成
- 上述是关于 p ( X ) p(\bm X) p(X)的讨论,但同样适用于 p ( x ∣ X ) p(\bm x|\bm X) p(x∣X),以及 p ( t ∣ x , X , T ) p(\bm t|\bm x, \bm X, \bm T) p(t∣x,X,T)等
14.2 Committees
委员会committe:训 L L L个不同的模型,然后取平均做预测
该方法主要是用来降variance,例如图3.5中的模型平均
- 自助聚集bootstrap aggregation/bagging:对数据集的重采样构造

其动机是,如果真实回归函数是 h ( x ) h(\bm x) h(x),模型输出则可以写成
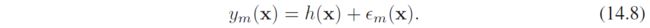
平均平方和损失为

各个模型独立预测的平均误差为

式14.7的委员会方法预测的期望误差为

如果假定误差是0均值且不相关的,即
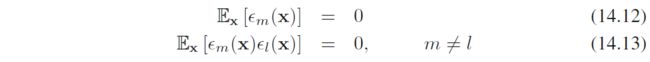
那么易得
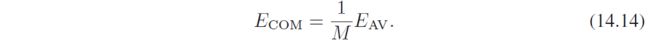
不过有一个严重的问题,就是需要假设每个模型之间是不相关的,但是实际中,误差通常相关性很高。导致增益很小。不过可以证明, E C O M ⩽ E A V E_{COM}\leqslant E_{AV} ECOM⩽EAV(习题14.3,14.4,好像需要误差函数关于预测值是凸的),也即委员会一定是比单个模型的平均误差有提升的
14.3 Boosting
提升方法boosting:是committee的变种,串行学一堆模型,依据之前模型的表现调整误差函数
相比于委员会,boosting希望能得到更多的提升。就算基分类器的性能仅仅稍好于随机猜测,即弱分类器,boosting也能有很好的表现
P659 最小化指数误差
提升方法起源于统计学习理论,得到泛化误差上界,不过这些上界非常宽松,没有实际价值
Friedman et al. (2000)给出了一种不同的boosting解释,说明adaboost是关于指数误差的序列最小化
考虑指数误差函数
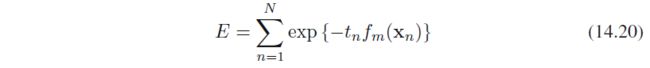
其中

t n ∈ { − 1 , 1 } t_n\in \{-1, 1\} tn∈{−1,1}是label,目标是最小化 α , y \alpha,y α,y
假定 y 1 , … , y m − 1 , α 1 , … , α m − 1 y_1,\dots, y_{m-1},\alpha_1, \dots,\alpha_{m-1} y1,…,ym−1,α1,…,αm−1给定,只关于 α m , y m \alpha_m,y_m αm,ym最小化,误差函数可以写成

其中 w n ( m ) = exp { − t n f m − 1 ( x n ) } w_n^{(m)}=\exp \{-t_n f_{m-1}(\bm x_n)\} wn(m)=exp{−tnfm−1(xn)},记 T m \mathcal T_m Tm为 y m y_m ym分对的数据集合, M m \mathcal M_m Mm是分错的数据集合,那么误差函数可以写为
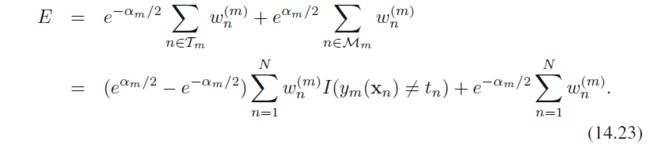
上式关于 y m y_m ym的优化,第二项是常量,所以实际上就是在优化式14.15;关于 α m \alpha_m αm的优化,得到了式14.17. 这都是和AdaBoost的算法流程里一致的
接着考察 w w w,从式14.22注意到

使用代换
![]()
得到
![]()
其中 exp ( − α m / 2 ) \exp(-\alpha_m/2) exp(−αm/2)独立于 n n n,对所有项都一样,丢掉不影响结果,由此得到式14.18
最后做决策时, f f f中的系数 1 / 2 1/2 1/2也可以丢掉,而不影响符号
P661 boosting的误差函数
为了获得更多关于指数误差函数的直觉insight,考虑如下误差函数

由变分法求上式关于 y y y的最小化,易得
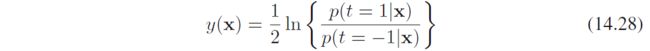
所以它是log-odd函数 ln ( x / ( 1 − x ) ) \ln(x/(1-x)) ln(x/(1−x))缩放一半,也即AdaBoost在基分类器的线性组合形成的函数空间中寻找log-odd函数的形式,同时受约束于序列优化策略
在交叉熵损失中,如果 t ∈ { − 1 , 1 } t\in \{-1, 1\} t∈{−1,1},则一个数据点的误差函数可以写为 ln ( 1 + exp ( − y t ) ) \ln (1+\exp (-yt)) ln(1+exp(−yt)),(回顾7.1.2节)
不同loss function的比较如图所示
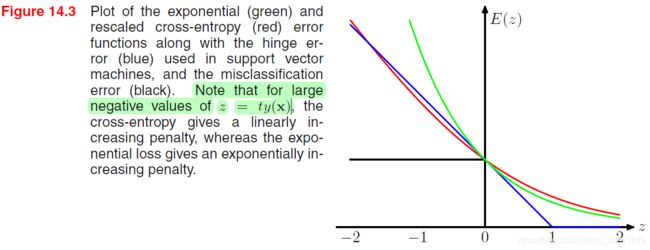
上图中,为了把所有loss都规约到 ( 0 , 1 ) (0,1) (0,1)点,cross-entropy除以 ln 2 \ln2 ln2
- 最小化cross-entropy,导出逻辑回归
- 最小化hinge-loss,导出SVM
- 序列最小化指数损失,导出AdaBoost
指数损失的缺点:
- 过度惩罚了 t y ( x ) ty(\bm x) ty(x)过小的情况,所以指数损失没有cross-entropy那样对离群点鲁棒
- 指数函数不能解释成某个定义很好的概率模型的对数似然(习题14.8)
- 难以扩展到多类情况(周志华-《集成方法》一书2.5节中给出了几种扩展)
把提升方法表示为指数误差下可加性模型的最优化,扩展出一大类相似算法——包括使用其他误差函数的多类推广和回归。在回归中,如果用平方和损失,那么序列最小化的新增模型就变成了拟合残差 t n − f m − 1 ( x n ) t_n - f_{m-1}(\bm x_n) tn−fm−1(xn),也即梯度提升(Friedman 2001),可以参考《统计学习方法》
(《西瓜书》第8章阅读材料指出:AdaBoost不容易过拟合,但是理论上仍然很难解释。这个现象的的严格表述是“为什么AdaBoost在训练误差达到0之后,继续训练,仍能提高泛化性能”,如果一直训练下去,过拟合终将出现)
14.4 Tree-based Models
决策树Decision Tree:如何看作是组合模型?决策树可以认为是从一堆模型中选一个,做决策,而不是平均。即对不同的输入区域用不同的模型。总复杂度随着输入有关的选择复杂程度变化
- CART classification and regression trees
决策树的构造其实算是一种贪心算法,也即先贪心出根节点,再贪心出下一层……整体来看,并不一定是最优划分
-
关于停止:常见的做法是先构建一棵较大的树,然后用叶子上样本点数量作为停止准则,再后剪枝。剪枝会在模型复杂度和误差之间平衡。例如,从树 T 0 T_0 T0开始,通过剪枝得到 T T T,即 T ⊂ T 0 T\subset T_0 T⊂T0. 假定叶结点的索引为 τ = 1 , … , ∣ T ∣ \tau=1,\dots,|T| τ=1,…,∣T∣,其中 ∣ T ∣ |T| ∣T∣表示叶子个数。对于具有 N τ N_\tau Nτ个数据点的区域 R τ \mathcal R_{\tau} Rτ,给出的最优预测为
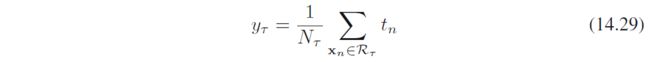
对应平方和损失

剪枝准则为
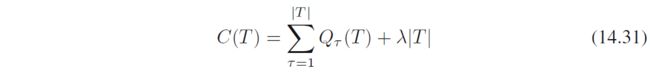
其中 λ \lambda λ平衡了模型复杂度(由 ∣ T ∣ |T| ∣T∣定义)与平方和损失,该值通过cross-validation选择 -
对于分类问题,常用的损失函数是交叉熵和基尼系数,这一块直接翻西瓜书。这两者比分类错误率要好,因为这两者对结点的概率更敏感(习题14.11),此外这两者是可微的。对于后剪枝,分类错误率则更常用
-
决策树的一个优点是,所学习的模型人能理解。但是实际中,训练集的微小改变有可能形成非常不同的划分
-
决策树的问题在于
- 沿着特征空间平行于坐标轴的方向划分,如果要斜着划分,往往要很多次分裂
- 回归中,预测是不连续的,不光滑
14.5 Conditional Mixture Models
决策树是一种很硬的、平行于坐标轴的区域划分,可以采用一种概率模型去进行组合
P667 线性回归模型的混合
考虑 K K K个线性回归模型,每一个都有参数 w k \bm w_k wk,共用一套噪声精确度 β \beta β,先考虑一维输出 t t t,尽管扩展到多维是容易的。记混合系数为 π k \pi_k πk,混合分布可以写为

其中 θ \bm \theta θ表示了所有参数,包括 W = { w k } , π = { π k } , β \bm W=\{\bm w_k\},\bm \pi=\{\pi_k\},\beta W={wk},π={πk},β
对数似然为

该式可用EM优化,其中隐变量 z n k ∈ { 0 , 1 } z_{nk} \in \{0,1\} znk∈{0,1},对于每个数据点 n n n,只有一个 z n k = 1 z_{nk}=1 znk=1,其他为 0 0 0

全数据对数似然为
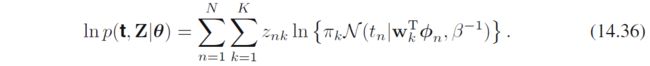
EM中
- E步,首先用 θ o l d \bm \theta^{old} θold,得到后验分布
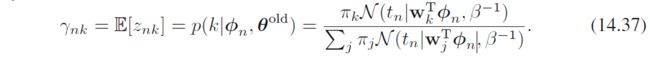
其中 γ n k \gamma_{nk} γnk就是后验,或者叫“责任responsibility” - M步:根据式14.36,得到Q函数为

上式其实就是把期望套在式14.36的 z n k z_{nk} znk上
算 π , W , β \bm \pi,\bm W,\beta π,W,β
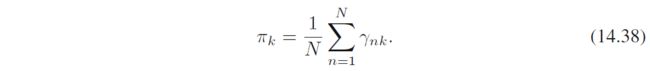
该式和混合高斯式9.22一样,这也是符合直觉的
考虑关于 w k \bm w_k wk的优化,只关注有关项
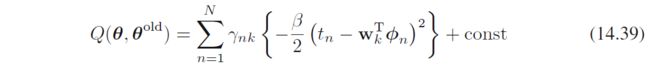
这其实就是带权最小二乘weighted least squares,注意这 K K K个不同的部分其实是互不干扰的,所以关于 w k \bm w_k wk求导得到

写成矩阵形式

其中 Φ T = ( ϕ 1 , … , ϕ N ) \Phi^T=(\bm\phi_1, \dots, \bm\phi_N) ΦT=(ϕ1,…,ϕN), R k = diag ( γ n k ) ∈ R N × N \bm R_k=\text{diag}(\gamma_{nk}) \in \mathbb R^{N\times N} Rk=diag(γnk)∈RN×N
解得

观察这个式子,原先的线性回归解析解可以认为是 R k = I N \bm R_k=\bm I_N Rk=IN,另外,这和逻辑回归的迭代重加权平方算法——式4.99一致(感觉是个梦幻联动,暂时没想清楚背后的联系)
最后,优化 β \beta β,只保留有关项
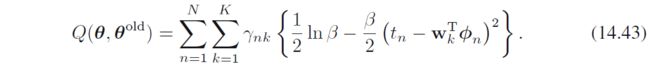
极值点为
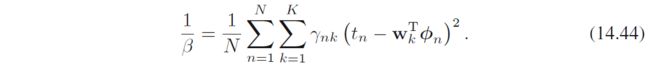
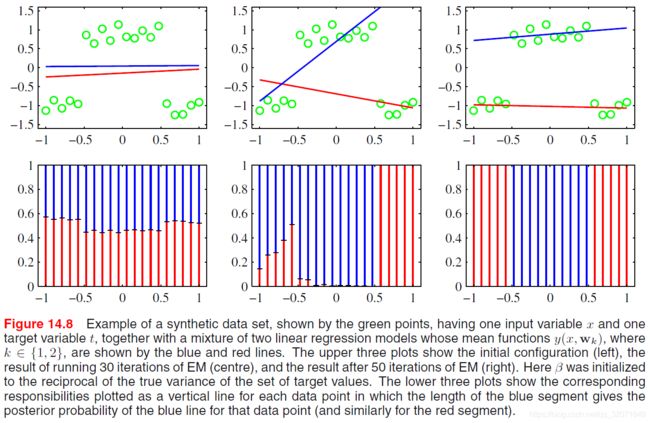
- 图14.8的后验是很好的的,从图14.9看用两个线性分量比用单个要得到更好的数据表示,似然也高了
- 不过这里 π \pi π和 x x x无关,所以如果从做预测的角度考虑,给定一个 x x x,也判断不出来该用哪个分量;也即还是拟合了很多没有数据的区域
一种修正的扩展是把混合系数 π \bm \pi π也表示成 x \bm x x的函数,得到类似5.6节的混合密度网络,或14.5.3节的层次混合专家模型 - 注意,如果要做点估计,根据1.5.5节决策论,均方误差损失最小的对应预测均值,也即 ∑ k = 1 K π k E [ t ∣ ϕ ^ , w k , β ] \sum_{k=1}^K \pi_k \mathbb E[t|\hat \phi, \bm w_k, \beta] ∑k=1KπkE[t∣ϕ^,wk,β],从图14.9看,这是个很差的结果,位于两条高概率的中间低概率区域(参考习题14.15)
P670 逻辑回归模型的混合
将 K K K个逻辑回归模型混合
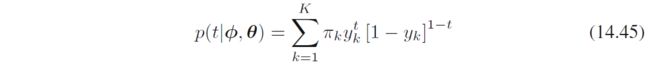
其中 ϕ \bm \phi ϕ是特征向量, y k = σ ( w k T ϕ ) y_k=\sigma(\bm w_k^T\bm \phi) yk=σ(wkTϕ)是第 k k k个分量的输出, θ \bm \theta θ包括 { π k } \{\pi_k\} {πk}和 { w k } \{\bm w_k\} {wk}
对应数据集似然函数形式为

全数据的概率分布为

其中 z n k z_{nk} znk是一个二值变量。(可以把式14.47关于 Z \bm Z Z求和求掉,验证式14.46)
使用EM
- E步:得到 z z z的后验分布

同线性回归, γ \gamma γ叫做“责任responsibility” - M步:全数据的Q函数为
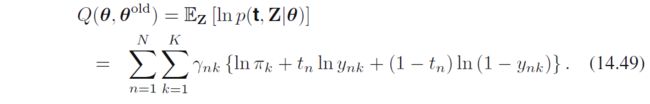
需要优化 π , W \bm \pi, \bm W π,W
关于 π \bm \pi π的优化得到熟悉结果
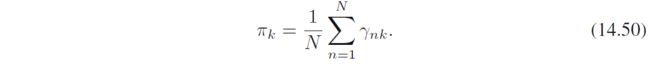
关于 W \bm W W的优化,注意到不同分量不干扰,此外,没有解析解,所以采用4.3.3节的迭代重加权平方terative reweighted least squares (IRLS)算法(其实就是牛顿法)。关于 w k \bm w_k wk的梯度和Hessian矩阵分别为
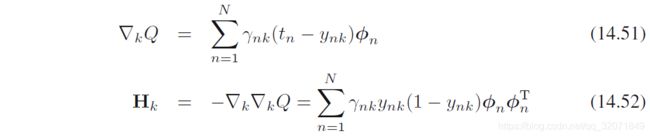
这里无非是多加了个权,其他和4.3.3节结果一致
- 混合逻辑回归可以直接扩展到多分类问题(习题14.16)
P672 混合专家 mixtures of experts
和混合线性(逻辑)回归的区别在于,混合系数 π \pi π也变成输入的函数
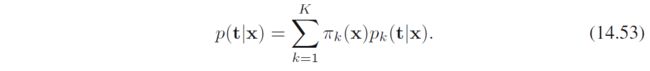
其中混合系数 π k ( x ) \pi_k(\bm x) πk(x)称为门函数gating functions(总感觉有点attention那味了), p k ( t ∣ x ) p_k(\bm t|\bm x) pk(t∣x)称为专家experts
其背后的思想是不同的专家在自己的区域进行预测,门函数确定哪个分量控制哪个区域
其中门函数必须满足混合系数通常的限制,即 0 ⩽ π k ( x ) ⩽ 1 , ∑ k π k ( x ) = 1 0\leqslant \pi_k(\bm x)\leqslant 1,\ \sum_k \pi_k(\bm x)=1 0⩽πk(x)⩽1, ∑kπk(x)=1,所以可以通过softmax进行约束表示
如果专家也是线性(回归、分类)模型,那么整体模型可以用EM算法优化,M步中需要用IRLS算法
P673 层次混合专家 hierarchical mixture of experts (HME)
专家模型的限制在于门函数和专家函数都是线性的。更灵活的模型是用多层门函数,得到层次混合专家hierarchical mixture of experts (HME模型),想象一个混合分布,其中每个部分都是混合分布。如果系数不是输入依赖的,那么这种层次和单层没区别,但是输入是线性依赖的,那么就有区别
参考习题14.17,这题的解答值得一看,如图
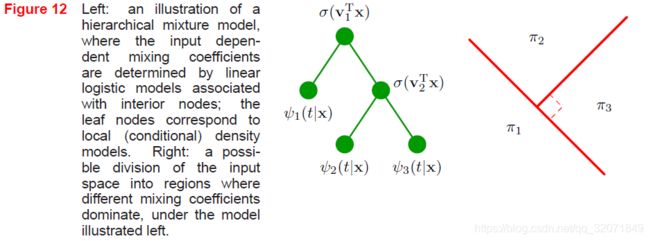
例如这种区域划分方式,用三类softmax就构造不出来,主要是 π 1 \pi_1 π1不受 v 2 T \bm v_2^T v2T影响的大区域(也即右图的红色直线),softmax一定互相干扰
- 该模型可以看作是决策树的概率版本。(这感觉和神经网络也有点像,中间用softmax激活,输出是最终的混合系数,不过每一层都接收输入,可能不是隐层传递)
该模型可以用EM优化,其中M步要用IRLS - Bishop and Svensén(2003)提出了一种贝叶斯HME,并变分推断求解
- HME和5.6节的混合密度网络有紧密联系
- HME的一个优点是可以用EM优化,M步关于混合分量和门函数是凸优化(虽然整体目标函数非凸)
- 混合密度网络的优点是分量和混合系数共享隐层单元,且对输入空间的划分更松,划分除了软、不限于坐标轴平行外,还可以是非线性的
参考文献:
[1] Christopher M. Bishop. Pattern Recognition and Machine Learning. 2006
*后记
至此,PRML读完了
2020年11月7日