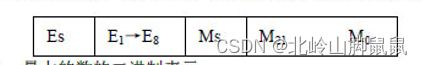计算机组成原理——32位浮点数的不同表示

一般现在普遍见到的32位浮点数可能会有以下两种结构：

第一种：

Es：阶符                              Ms：数符

E1~E8：阶码                        M21~M0：尾数

————————————————分割线————————————————————————

第二种：  

 这个如图所示。

在IEEE754标准中规定的阶码部分用移码来表示。

一个规格化的32位浮点数x的真值表示为x=(-1)^S*(1.M)*2^(E-127) , e=E-127,e是指数。

移码的表示的范围是0~255，对应的指数e的范围就是-127~+128.

IEEE754标准中的规定：

1.若E=255=11111111B,且M<>0,则真值N为无穷大，结合数符位的不同，分为正无穷和负无穷：

   （1）正无穷：1 11111111 000 0000 0000 0000 0000 0000

      (2) 负无穷：  0 11111111 000 0000 0000 0000 0000 0000

2.若E=0=00000000B,且M=0,则真值N为0，根据数符位的不同，分为正0和负0：

      (1) 正0：0 00000000 000 0000 0000 0000 0000 0000

       (2)负0: 1 00000000 000 0000 0000 0000 0000 0000

去除0和255这两种特殊情况，那么指数e的取值范围就是1-127=-126到254-127=127

3.若0是选了127之后，剩下的数的公式。指数e的表示范围变成-126~127

在IEEE754标准下

正数的最大值为：0 11111110 111 1111 1111 1111 1111 1111，

表示：(2 - 2^(-23))*2^(127)约等于2 * 2 ^ (127)

负数的最小值为：1 11111110 111 1111 1111 1111 1111 1111，

表示：(-1)* (2 - 2^(-23))*2^(127)约等于-2 * 2 ^ (127)

正数的最小值为：0 00000001 000 0000 0000 0000 0000 0000

表示 ：1 * 2 ^ (-126)

负数的最大值为：  1 00000001 000 0000 0000 0000 0000 0000

表示：-1*2 ^ (-126)

以上就是IEEE754标准中的情况。

-----------------------------------------------------分割线——————————————————————

当尾数部分用补码来表示这是另一种情况，首先声明，用补码表示尾数时是默认没有前置1的。   阶码依然是用移码表示。这里的偏移值选择的是128的情况下。阶码的范围是0~255，指数的范围是-128~127

规定：尾数为补码，必须是最高数值位和符号位相反。哪来的奇怪规定

规定：尾数为补码，必须是最高数值位和符号位相反。哪来的奇怪规定

规定：尾数为补码，必须是最高数值位和符号位相反。哪来的奇怪规定(重要的事说三遍)

数符为0,这个数就是正数,正数补码就是其本身,其最高有效位(阶码使用标准移码的话规格化后尾数最高有效位就是小数点后第一位)必定为1,数符0和最高有效位的1相异.
数符为1,这个数就是个负数,求负数的补码有一步叫按位取反(一般来说浮点数可以存储的有效位不会小于6位),原本最高有效位的1变成了0,所以数符1和最高有效位的0相异.

你看懂了吗？

最大的正数：0 1111 1111 111 1111 1111 1111 1111 1111

表示：(1-2^(-23)) * 2^(127)

最小正数：0 0000 0000 100 0000 0000 0000 0000 0000

表示：2^(-1)*2^(-128)

最大负数：1 0000 0000 011 1111 1111 1111 1111 1111

表示：-(2^(-1)-2^(-23))*2^(-128)

最小负数：1 1111 1111 000 0000 0000 0000 0000 0000

表示：-1*2^(127)