2023/4/2总结
题解
线段树OR树状数组 - Virtual Judge (vjudge.net)
正如这道题目一样,我的心情也如此。
1.这道题是线段树问题,更改学生值即可,不需要用到懒惰标记。
2.再去按照区间查找即可。(多组输入,拿20多次提交换来的)
代码如下:
#include
#define N 200010
int a[N];
struct node
{
long long maxnum;
}arr[N*10];
long long max(long long a,long long b)
{
if(a>b) return a;
return b;
}
int creat(int l,int r,int k)
{
if(l==r)
{
arr[k].maxnum=a[l];
return 0;
}
int mid;
mid=(l+r)/2;
creat(l,mid,k*2);
creat(mid+1,r,k*2+1);
arr[k].maxnum=max(arr[k*2].maxnum,arr[k*2+1].maxnum);
}
long long Uoper(int l,int r,int pos,int add,int k)
{
if(l>r) return 0;
if(pos>r||pos=pos)//如果在左子树
{
Uoper(l,mid,pos,add,k*2);
}
else
{
Uoper(mid+1,r,pos,add,k*2+1);
}
arr[k].maxnum=max(arr[k*2].maxnum,arr[k*2+1].maxnum);
}
long long Qoper(int l,int r,int x,int y,int k)
//l,r是当前的区间,x,y是需要访问的区间
{
long long sum=0;
if(x>y) return 0;
if(x<=l&&r<=y) return arr[k].maxnum;
int mid=(l+r)/2;
if(y<=mid)
{
sum=max(sum,Qoper(l,mid,x,y,k*2));
}
else if(x>mid)
{
//如果右子树包含
sum=max(sum,Qoper(mid+1,r,x,y,k*2+1));
}
else
{
//俩边都有
//需要拆分区间,左边拆成x,mid
sum=max(Qoper(l,mid,x,mid,k*2),Qoper(mid+1,r,mid+1,y,k*2+1));
}
return sum;
}
int main()
{
int n,m,i,j,x,y;
char str[3];
long long sum=0;
while(~scanf("%d%d",&n,&m))
{
for(i=1;i<=n;i++)
{
scanf("%d",&a[i]);
}
creat(1,n,1);
for(i=1;i<=m;i++)
{
scanf("%s",str);
if(str[0]=='U')
{
scanf("%d%d",&x,&y);
Uoper(1,n,x,y,1);
}
if(str[0]=='Q')
{
scanf("%d%d",&x,&y);
sum=Qoper(1,n,x,y,1);
printf("%lld\n",sum);
}
/* for(j=1;j<=9;j++)
{
printf("%lld ",arr[j].maxnum);
}
puts("");*/
}
}
return 0;
} 线段树OR树状数组 - Virtual Judge (vjudge.net)
1.这道题是需要用到懒惰标记的。
懒惰标记是指,在我们能找到的区间,我们先把这个区间总和加上懒惰值乘以 r-l+1,我们加一个存储需要在这个区间内加的值,保存起来。
2.下次如果访问到这个区间的子区间,子区间继承父区间的懒惰值就可以。
3.在访问的时候如果没有刚好访问到我们想要的区间,我们就需要查看该点的懒惰值,是否存在,存在就需要传递到子区间,也就是左区间和右区间。还需要把该点的懒惰值消去
4.然后找到我们所需要的区间加上继承的懒惰值即可。(如果不对就换一个编译器吧)
代码如下:
#include
#define N 100010
long long a[N];
struct node
{
long long sum;
}arr[N*4];
long long mark[N*4];
void init()
{
int i;
for(i=0;ir) return ;
if(l==r)
{
arr[k].sum=a[l];//底层
return ;
}
int mid=(l+r)/2;
creat(l,mid,k*2);
creat(mid+1,r,k*2+1);
arr[k].sum=arr[k*2].sum+arr[k*2+1].sum;//左子树和右子树
}
void down(int k,int l,int r)
//l是指区间长度
{
if(mark[k])//当前标记了,数组里面存储了数据,需要往上保存
{
mark[k*2]+=mark[k];//左子树
mark[k*2+1]+=mark[k];//右子树
int mid=(l+r)/2;
arr[k*2].sum+=mark[k]*(mid-l+1);
//左子树的总和加上应该传下去的懒惰标记
//懒惰标记为l-l/2是左子树的个数
arr[k*2+1].sum+=mark[k]*(r-mid);
//右子树的总和加上应该接到的懒惰标记
//l/2是右子树的个数
mark[k]=0;//已经把标记传给下面了,而且左子树和右子树也已经加上值了
}
}
void Coper(long long l,long long r,long long x,long long y,long long k,long long add)
{
if(x>r||y=r)//代表xy区间包含了当前区间
{
arr[k].sum+=(r-l+1)*add;//先加上总和
mark[k]+=add;//这个区间标记懒惰标记
return ;
}
down(k,l,r);//如果不是该区间则需要把当前区间内标记
int mid=(l+r)/2;
if(x<=mid) Coper(l,mid,x,y,k*2,add);//左子树
if(y>mid) Coper(mid+1,r,x,y,k*2+1,add);//右子树
arr[k].sum=arr[k*2].sum+arr[k*2+1].sum;
//左子树和右子树已经算出来了,需要更新值
}
long long Qoper(long long l,long long r,long long x,long long y,long long k)
{
if(x<=l&&y>=r) //代表访问区间比当前区间要大
{
return arr[k].sum;
}
if(x>r||ymid) sum+=Qoper(mid+1,r,x,y,k*2+1);//右子树
return sum;//返回当前能得到的值
}
int main()
{
long long n,m,i,j,x,y,add;
char str[3];
// while(~scanf("%lld%lld",&n,&m))
// {
scanf("%lld%lld",&n,&m);
// init();
for(i=1;i<=n;i++)
{
scanf("%lld",&a[i]);
}
creat(1,n,1);
for(i=1;i<=m;i++)
{
scanf("%s",str);
if(str[0]=='C')
{
scanf("%lld%lld%lld",&x,&y,&add);
Coper(1,n,x,y,1,add);
}
else
{
scanf("%lld%lld",&x,&y);
printf("%lld\n",Qoper(1,n,x,y,1));
}
// for(j=1;j<=19;j++)
// {
// printf("--%lld %lld\n",j,arr[j].sum+mark[j]);
// }
}
// }
return 0;
} 线段树OR树状数组 - Virtual Judge (vjudge.net)
1.这是一道区间修改加懒惰标记的问题
2.我们访问到所需要的区间,然后改变懒惰值就可以,不需要加减,直接赋值总和和懒惰值。
3。最后输出根节点的值即可,因为根节点存储的就是1-n的总和。
代码如下:
#include
#define N 100010
int hook[N*4];
int mark[N*4];
int creat(int l,int r,int k)
{
// puts("*");
mark[k]=0;
if(l==r)
{
hook[k]=1;
return 0;
}
int mid=(l+r)/2;
creat(l,mid,k*2);
creat(mid+1,r,k*2+1);
hook[k]=hook[k*2]+hook[k*2+1];
return 0;
}
void down(int l,int r,int k)
{
int mid=(l+r)/2;
if(mark[k])
{
mark[k*2]=mark[k];
mark[k*2+1]=mark[k];
hook[k*2]=mark[k]*(mid-l+1);
hook[k*2+1]=mark[k]*(r-mid);
mark[k]=0;
}
}
int change(int l,int r,int k,int x,int y,int newhook)
{
// printf("%d %d\n",l,r);
if(x<=l&&y>=r)
{
hook[k]=(r-l+1)*newhook;
mark[k]=newhook;
return 0;
}
int mid=(l+r)/2;
down(l,r,k);
if(y<=mid)
{
change(l,mid,k*2,x,y,newhook);
}
else if(x>mid)
{
change(mid+1,r,k*2+1,x,y,newhook);
}
else
{
change(l,mid,k*2,x,mid,newhook);
change(mid+1,r,k*2+1,mid+1,y,newhook);
}
hook[k]=hook[k*2]+hook[k*2+1];
}
int main()
{
int t,n,m,i,j,x,y,z;
scanf("%d",&t);
for(i=1;i<=t;i++)
{
scanf("%d%d",&n,&m);
creat(1,n,1);
// puts("*");
for(j=1;j<=m;j++)
{
scanf("%d%d%d",&x,&y,&z);
change(1,n,1,x,y,z);
}
printf("Case %d: The total value of the hook is %d.\n",i,hook[1]);
}
return 0;
} Problem - A - Codeforces
1.这道题直接暴力最多也就90次,暴力即可。
#include
int getLucky(int x)
{
int a[10],i,n,t=x,max=0,min=10;
for(i=0;t;i++)
{
a[i]=t%10;
t/=10;
if(a[i]>max) max=a[i];
if(a[i]max)
{
max=t;
temp=i;
}
if(max>=9)
{
temp=i;
break;
}
}
printf("%d\n",temp);
return 0;
}
int main()
{
int t,i,l,r;
scanf("%d",&t);
while(t--)
{
scanf("%d%d",&l,&r);
slove(l,r);
}
return 0;
} Problem - B - Codeforces
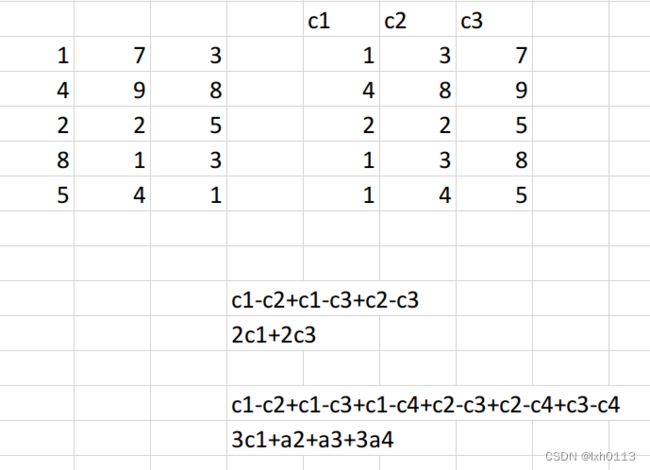
1.排序不改变最终的值,因为每一列(在这里我已经转换成行了),都要和自己对于那一列互相比较的。相减的次数是一样的。
2.然后就是会发现,相减去的过程中有些列会多次出现,会相互抵消。
(下面的图片已经行列转置了)
#include
#include
#include
using namespace std;
int main()
{
long long t,i,j,n,m,x;
long long res;
scanf("%lld",&t);
while(t--)
{
res=0;
scanf("%lld%lld",&n,&m);
vector > a(m,vector(n));
//声明一个m行n列的数组
for(i=0;i Problem - A - Codeforces
1.这一题说的是可以删除数字,使对应下标出现对应的值。
2.那么就是说如果是3是不能出现在1 2 的位置的,因为再怎么删掉,也不会让这个序列成为漂亮序列。
3.暴力即可
#include
#define N 120
int a[N];
int main()
{
int t,n,i,j,flag;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
flag=0;
for(i=1;i<=n;i++)
{
scanf("%d",&a[i]);
}
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
//
if(a[j]<=(j-i+1))
{
flag=1;
break;
}
}
if(flag) break;
}
if(flag) puts("YES");
else puts("NO");
}
return 0;
} Problem - B - Codeforces
1.这道题不是bfs。因为得出的数字是按照2x+1和2x-1的来,所以我们可以知道,这个的来的数字一定不会是偶数。
2.它一定是奇数,然后一个奇数/2我们能得到 一个奇数和一个偶数,会有俩种情况,奇数大于偶数或者偶数大于奇数。
3.对于奇数大于偶数这个情况,我们知道,这个数字一定是通过2x-1的来的,因为产生的过程中是不会有偶数的。对于偶数大于奇数这个情况,这个数字 一定是2x+1来的。我们保存路径即可
代码如下:
#include
#include
#include java知识点
访问文件和目录
File类可以使用文件路径字符串创建File实例,该文件路径字符串既可以是绝对路径,也可以是相对路径。
访问文件名方法:
getName()返回File对象所表示的文件名称或者路径名称
getPath()返回次File对象所对应的路径名称
getAbsoluteFile()返回此File对象的绝对路径
检测文件相关方法
exists()判断File对象所对应的文件或者目录是否存在
isFile()判断File对象所对应的是否是文件,而不是文件夹
length()获取文件内容长度
creatNewFile()如果File对象所对应的文件不存在时,则新建一个File对象所指定的新文件,创建成功返回true否则返回false
delete()删除File对象所对应的文件或者路径
mkdir()创建一个File对象所对应的目录,创建成功返回true否则返回false
list()返回File对象的索要子文件名称和路径名称到string数组
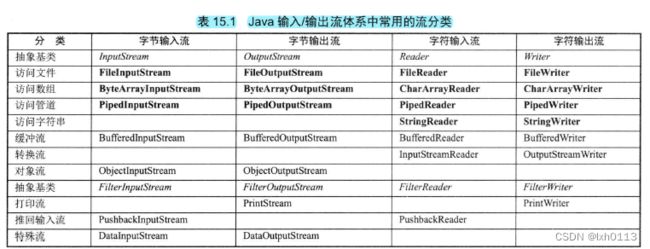
IO流
不同的输入输出流抽象表述为流。
按照流向可以分为输入流和输出流
按照操作数据单元可以分为字节流和字符流,字节流操作的数据单元式8位,而字符流操作单位是16位。
字节流主要又InputStream和OutputStream作为基类,字符流主要由Reader和Writer作为基类。
按照流的角色分为节点流和处理流。
向一个特地的IO设备读写数据的流称为节点流,节点流也叫低级流。
处理流用于队一个已经存在的流进行连接或者封装,通过封装后的流实现读/写功能,也叫做高级流。
InputStream/Reader OutputStream/Writer
InputStream/Reader所有输入流的基类,前面是字节输入流,后面是字符输入流。
OutputStream/Writer所有的输出流的基类,前面的字节输出流,后面的字符输出流。
操作方式:
InputStream/Reader
int read()读出单个字节返回所读的字节数据,int类型
int read(byte[] b)读出b数组大小的字节数据,并且存储在b数组当中
int read(byte[] b,int off,int len)读出len字节的数据存入数组b当中
OutputStream/Writer
write(int c)将一个整形数字所代表的字符写入
write(byte[]/char[] buf)将字节数组/字符数组中的数据输出到指定输出流
write(byte[]/char[] buf)将字节数组/字符数组中从off位置开始,长度位len的字节/字符输出到流当中
write(byte[],char[] buf,int off,int len)将数组中从off位置开始,长度位len的字节/字符输出到输出流当中
write(String str)将str字符串里面包含的字符输出到指定输出流当中
write(String str,int off,int len)将str字符串里面从off位置开始,长度为len的字符输出到指定输出流当中。
如果进行输入输出的内容是文本内容,则应该考虑使用字符流,如果进行输入输出的内容是二进制内容,则应该使用字节流。
转换流
InputStreamReader将字节输入流转换成字符输入流,OutputStreamWriter将字节输出流转换成字符输出流
推回输入流
PushbackInputStream和PushbackReader
unread(byte[]/char buf)将应该字节字符数组内容推回到缓冲区里面,允许重复读取刚刚读取的内容
unread(byte[]/char b,int off,int len)将应该字节/字符数组从off开始,长度为len字节的内容推回到缓冲区里面
unread(int b)将一个字节退回到缓冲区里面
读写其他进程的数据
InputStream getErrorStream()获取子进程的错误流
getInputStream()获取子进程的输入流
getOutputStream()获取子进程的输出流
RandomAccessFIle类
它可以读取文件内容,也可以向文件输出数据,支持随机访问,也就是说可以跳转到文件任意的地方读写数据。但是它只能读写文件,不能读写其他IO节点
getFilePointer()返回文件记录指针的当前位置
seek()将文件记录指针定位到pos位置
RandomAccessFile既可以读也可以写,它包含了InputStream的三个read()方法,也包含了OutputSream()的三个write()方法。
RandomAccessFile由俩个构造器,一个使用String参数来指定文件,一个使用File参数来指定文件,还需要另外一个mode参数,该参数指定RandomAccessFile的访问模式
r以只读方式打开
rw以读写方式打开,不存在创建新文件
对象序列化
序列化机制允许java对象转换成字节序列,这些字节序列可以保存在磁盘上,或者网络传输,以备以后重新恢复成原来的对象。具体是指将一个java对象写入到IO流中,对象的反序列则从IO流中恢复该java对象。
如果需要让某个对象支持序列化机制,则它的类是可序列化的。需要实现俩个接口Serializable,Externalizable。
所有可能在网络上传输的对象的类都应该是可序列化的。
实现序列化对象:创建一个ObjectOutputStream,这个输出流是一个处理流,调用ObjectOutputStream对象的writeObject()方法输出可序列化对象。
如果希望恢复java对象,需要反序列化,创建一个ObjectInputStream输入流,调用ObjectInputStream对象的readObject()方法读取流中的对象。反序列对象时,必须提供该java对象所属类的class文件夹。
如果一个类的成员变量的类型不是基本类型或者String类型,而是一个引用类型,这个引用类型必须时可序列化的,否则拥有该类的成员变量的类也是不可序列化的。
java序列化机制有一种特殊的序列化算法
所有保存到磁盘的对象都有一个序列化编号
如果该对象已经被序列化过,则该对象不会被再次序列化。
自定义序列化
通过在实例变量前面使用transient关键字修饰,可以指定java序列化时不序列化此实例变量。transient关键字只能用于修饰实例变量,不可以修饰java程序中其他的成份。