pca主成分分析结果解释_StatQuest 主成分分析（PCA)

微信公众号：生信小知识
关注可了解更多的教程及单细胞知识。问题或建议，请公众号留言;

StatQuest - 主成分分析(PCA)

https://www.bilibili.com/video/av54898361

内容目录

前言一维二维三维PCA原理PC1PC2画PCAScree Plot——树形图PCA一些TipsScaling (标准化)数据例子centering (中心化)数据期望主成分数目

前言

一维

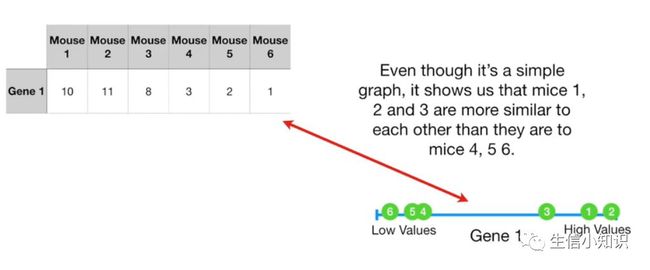
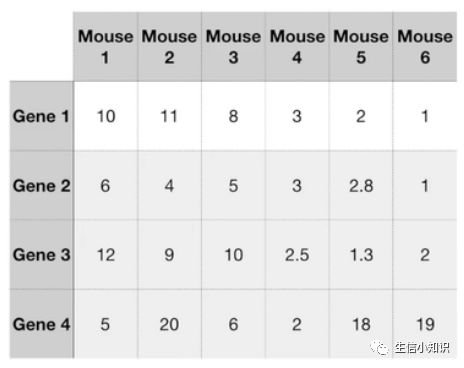
让我们从一组简单的数据开始，我们在 6 只不同的老鼠身上检测了基因 1 ：

我们只测量 1 个基因, 我们可以把数据标在一条数字线上，小鼠 1, 2 和 3 具有相对较高的值，小鼠 4, 5 和 6 具有相对较低的值。尽管这是一个简单的图表，但它显示出老鼠 1, 2 和 3 彼此之间的相似性比它们与小鼠 4, 5 和 6的相似性更强。

二维

如果我们测量了 2 个基因, 我们就可以在二维 x-y 图上绘制对应数据：

我们可以看到老鼠 1, 2 和 3 聚集在右边，小鼠 4, 5 和 6 在左下侧聚集。

三维

如果我们测量了 3 个基因, 我们会在图中添加另一个轴, 使它看起来像 3-D, 即三维的：

同理可以得到相似的结论。

如果我们测量了 4 个基因, 然而我们并不能再把所有数据绘制在图上，因为 4 个基因需要 4 个维度。

所以我们将讨论主成分分析(PCA)如何利用 4 个或更多的基因测量结果，4 个或更多维度的数据来绘制二维 PCA 图。

PCA原理

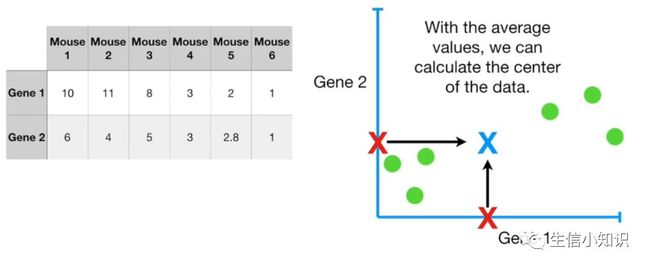
为了了解 PCA 的作用和工作原理，让我们回到只有 2 个基因的数据：

我们分别计算基因 1 和基因 2 的均值，利用平均值, 我们可以计算出数据的中心(图中蓝色的×)

现在我们将移动数据, 使中心位于图中原点 (0, 0) 上：

注: 整体移动数据并不会改变数据点之间的相对位置

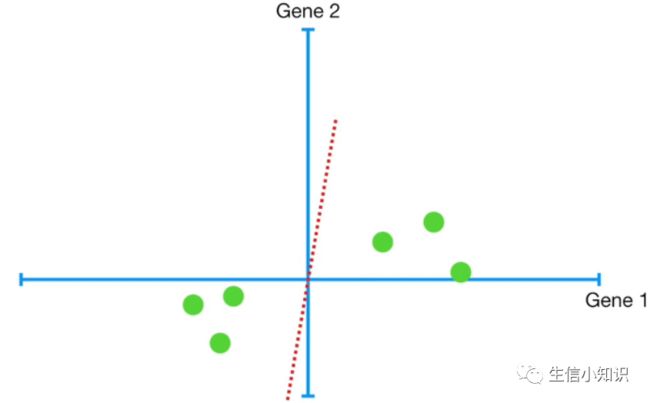
现在数据以原点为中心，我们可以试着拟合一条线上去：

我们需要了解 PCA 如何决定合适与否，我们首先随机画一条来穿过原点

为了量化这条线与数据的拟合程度, PCA 将数据投影到线上面，然后它可以测量从数据到线的距离并试图找到使这些距离最小化的线，或者可以尝试找到最大化从投影点到原点的距离的线。

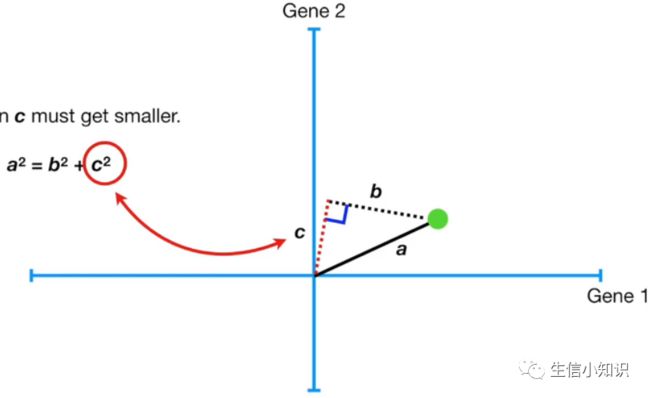
实际上从数据到线的最近距离的线和从投影点到原点距离最远的线是同一条：为了从数学的角度理解正在发生的事情, 让我们只考虑一个数据点：

这个点是固定的, 它与原点的距离也是固定的，换句话说, 当红色虚线旋转时, 从点到原点的距离是不会改变的。

当我们将点投影到直线上时，我们得到了一个在黑色虚线和红色虚线之间的直角，如图：

因为 a 和 a²不变，如果 b 变大了，那么 c 必须变小。

因此, PCA 可以最小化到直线的距离，或最大化从投影点到原点的距离。

直观地说, 最小化 b, 即点到线的距离更有意义，但实际上计算从投影点到原点的距离 c 更容易。

所以主成分分析通过最大化从投影点到原点的距离平方之和 (多个数据点时) 来确定最佳拟合线

所以对于这条线，PCA 将数据投影到线上，然后测量从这个点到原点的距离，让我们称之为 d。

d₁² + d₂² + d₃² + d₄² + d₅² + d₆² 这是我们测量的 6 个距离的平方和，我们称之为 SS(distances) 或平方距离之和

PC1

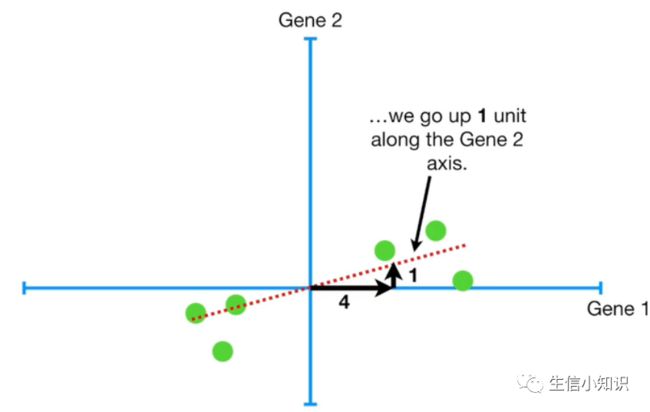
现在我们旋转线, 把数据投影到线上，然后求出从投影点到原点的平方距离之和，我们不停重复直到直线上投影点与原点之间的平方距离和最大，这条线叫做主成分1 (简称 PC1)。PC1 的斜率是 0.25：

这意味着数据主要沿着基因 1 轴分散的，只有一点点沿着基因 2 轴分散。要得到 PC1, 就要将 4 部分基因 1 与 1 部分基因 2 混合，基因 1 与基因 2 之比告诉你基因 1 在描述数据是如何分布的时候更重要。

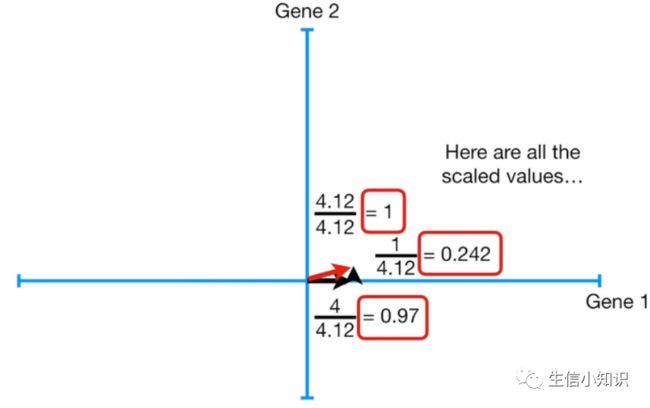
原先的 a² = b² + c²，把数值代入我们就得到了 a = 4.12，所以红线的长度是 4.12。当你使用 SVD 做 PCA 时, PC1 的长度被缩放为 1——我们所要做的就是把三角形按比例缩放, 使红线的长度为 1 个单位, 即每边除以 4.12，这是缩放后的值：

新的数值改变了我们的配比 (组成)，但是比例是一样的, 我们仍然使用 4 倍于基因 2 的基因 1 。

这个由 0.97 份基因 1 和 0.242 份基因 2 构成的 1 个单位长的向量被称为 PC1 的奇异向量或特征向量。每个基因的比例称为载荷分数 (Loading score)。

PCA 将最佳拟合线的  SS(distances) 称为 PC1 的特征值(距离原点平方和)。

PC1 的特征值的平方根叫做 PC1 的奇异值。

PC2

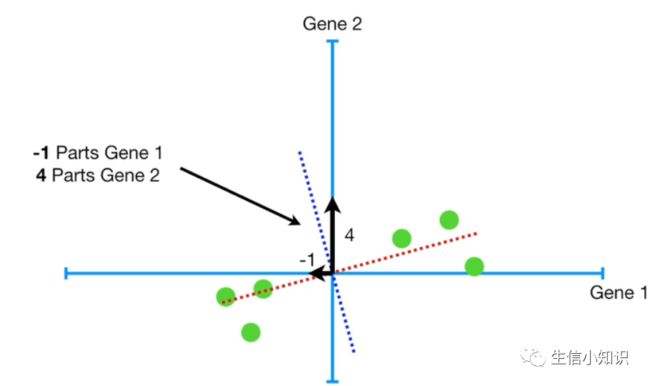
现在我们已经搞定了 PC1, 让我们看看 PC2(图中蓝虚线)，因为这只是一个二维图，PC2 只是一条穿过原点的线并垂直于 PC1，这意味着 PC2 的配比是 -1 份的基因 1 和 4 份基因 2。

如果我们对所有的东西进行缩放, 得到一个单位向量，这个单位向量的配比为 -0.242 份基因 1 和 0.97 份基因 2。

基因 2 比 基因 1 重要4 倍。

PC2 的特征值等于投影点和原点之间距离的平方和。

画PCA

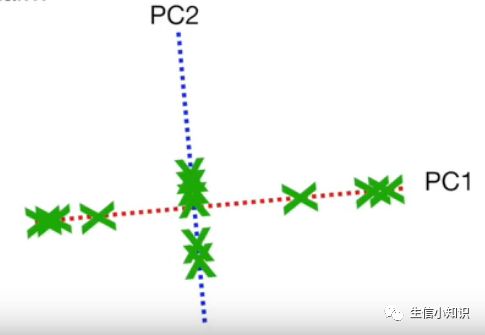
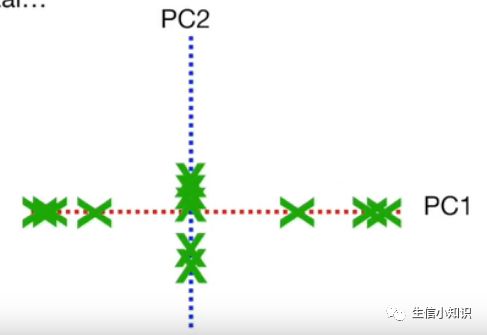
我们已经计算出 PC1 和 PC2，为了画出最终的主成分分析图, 我们只需旋转所有东西来使得 PC1 变得水平：

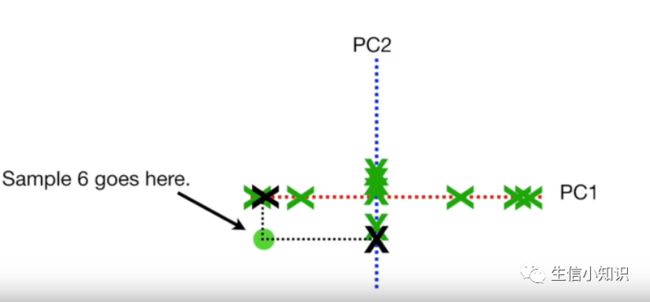
然后我们使用投影点找出样本在主成分分析图中的位置即可：

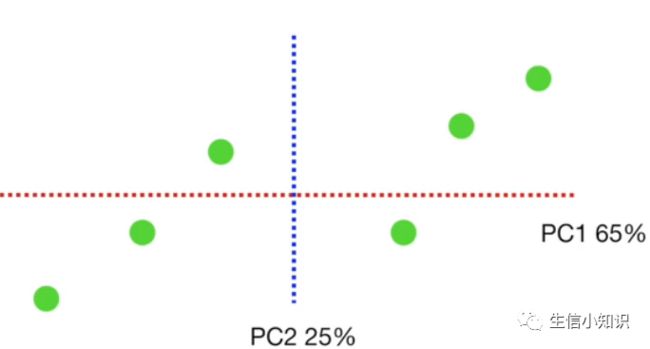
最后结果如下：

Scree Plot——树形图

我们把数据投影到主成分上来得到特征值——测量到原点的距离, 然后将它们平方并相加。

我们可以通过将特征值除以样本量减去 1, 将它们转换为原点 (0, 0) 周围的方差：

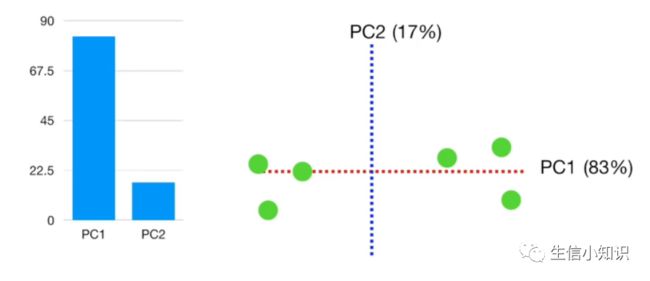
对于这个例子而言，假设 PC1 的方差为 15, PC2 的方差为 3。这意味这两个 PC 的总方差为 15 + 3 = 18。

也就是所 PC1解释了 15/18 = 0.83 = 83% 的主成分的总方差，PC2 解释了 3/18 = 17% 的主成分的总方差。

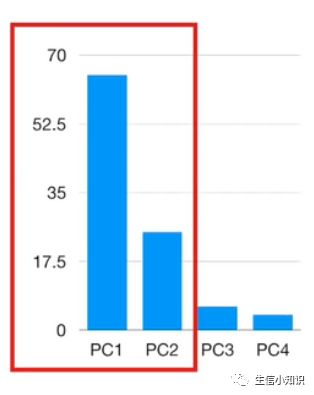
树形图是每个主成分所解释方差的百分比的图形化

我们再来看看有 3 个变量的 PCA，就意味着 3 个基因, 这和 2 个变量的情况几乎相同：

一旦计算出所有的主成分，就可以使用特征值, 即距离的平方和，来确定每个 PC 所解释方差的比例——PC1 解释了 79% 的方差，PC2 解释了 15% 的方差，PC3 解释了 6% 的方差

PC1 和 PC2 解释了绝大多数的方差，这意味只使用 PC1 和 PC2 的二维图将近似于 3D 图，因为它能解释数据的 94% 的方差。

如果每只老鼠测量 4 个基因, 我们就无法绘制出数据的四维图，但这并不能阻止我们做主成分分析，因为 PCA 核心不在于能否画出包含每个主成分的图，树形图能帮助我们做决定。

树形图：

这个例子里面，PC1 和 PC2 解释了总方差的 90%，所以我们可以用它们来绘制二维 PCA 图，所以我们把样品投影到前 2 个主成分上：

PCA一些Tips

Scaling (标准化)数据

数据的标准化与中心化以及R语言中的scale详解：https://blog.csdn.net/sl_world/article/details/80077466

所谓数据的标准化是指中心化之后的数据在除以数据集的标准差，即数据集中的各项数据减去数据集的均值再除以数据集的标准差。

例子

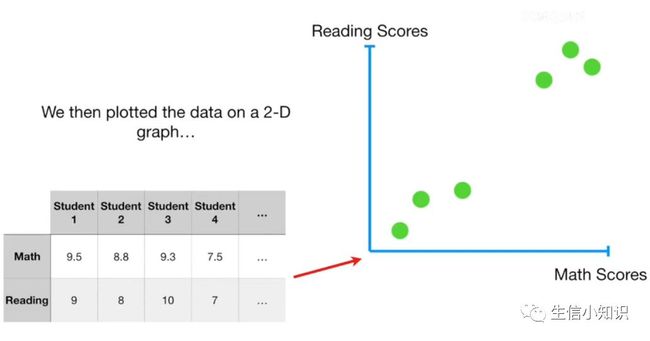
这里我们有一些学生的数学和阅读成绩：

我们来绘制数据：

数学分数从 0 到 100, 在图表中分布在 0 到 100 之间。

相比之下, 阅读成绩只有 0 到 10 分，在图表上它们都挤在 0 到 10 之间

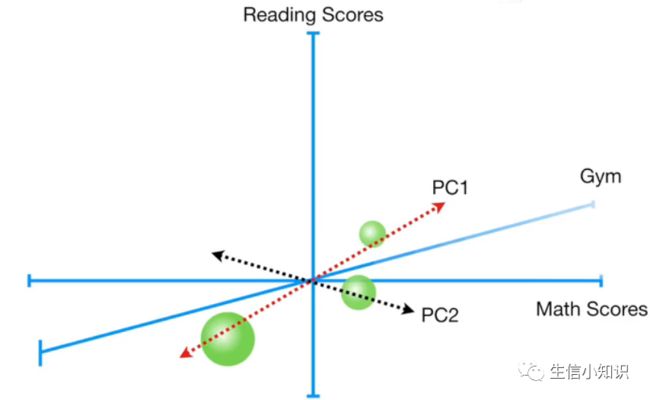
如果我们把数据中心化并做主成分分析，要构成PC1, 需要 0.99 份的数学成绩和 0.1 份的阅读成绩，这表明数学在捕获资质差异方面比阅读好 10 倍。

但这仅仅是因为数学分数在比例上比阅读分数大 10 倍

我们把数学分数除以 10 然后重新绘制，然后把数据中心化后再做主成分分析，要构成PC1, 需要 0.77 份的数学成绩和 0.77 份的阅读成绩：

这表明阅读和数学在捕获资质差异方面同等重要！！

这个故事的告诉你, 你需要确保么个变量的比例都是大致相当，否则你会偏向其中一个！

标准做法是将每个变量除以对应的标准差！！

如果一个变量有一个很宽的范围, 它将有一个很大的标准差，除以它会把数值标准化到一个比较集中的区域。

如果一个变量的范围很窄, 它将有一个小的标准偏差，除以它会把数值标准化到一个也比较集中的区域。

centering (中心化)数据

所谓数据的中心化是指数据集中的各项数据减去数据集的均值。

第一步数据中心化很重要, 但不是每个进行 PCA 的软件都默认进行中心化。

如果你没有进行中心化的情况下使用 SVD (奇异值分解) 做 PCA，它仍然会尝试将一条通过原点线与数据相拟合，你的主成分就不会像你所期望的那样。

因为还是通过了原点，所以可能拟合效果不好。

因此, 请仔细检查您正在使用的 PCA 程序是将数据中心化了或者你自己来先处理。

期望主成分数目

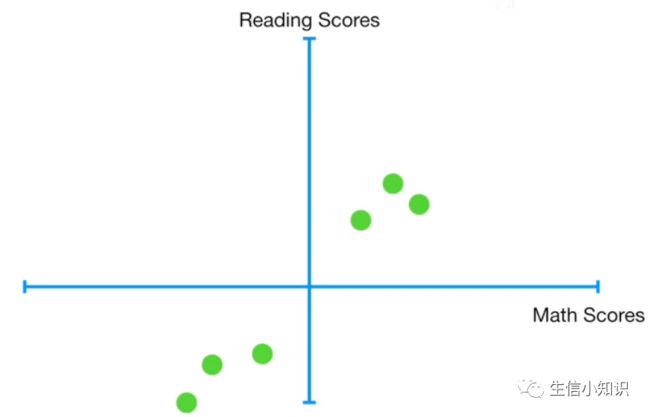
第一个例子里我们有一群学生的数学和阅读成绩，然后我们把数据绘制在二维图上

我们然后中心化数据：

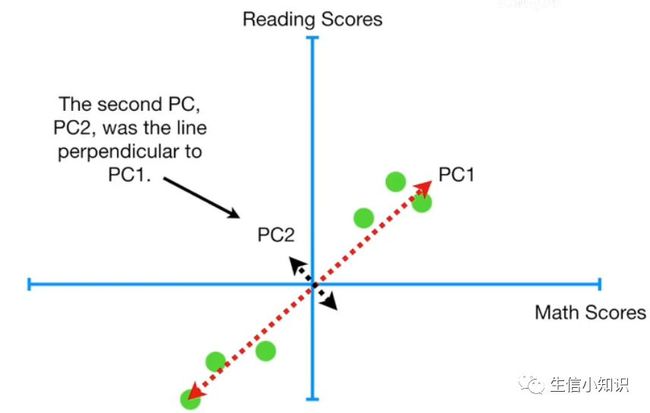
然后我们找到了穿过原点的最佳拟合线，这是 PC1：

第二个PC, PC2 是垂直于 PC1 的线：

然后现在我们有一个问题, 有没有第三个主要成分？——没有的，因为目前只有2个变量，也就是在二维空间，所以不可能有3个PC。

因此, 当我们测量每个样本 (学生) 的两个变量 (数学和阅读) 时，我们最多可以有两个主成分。

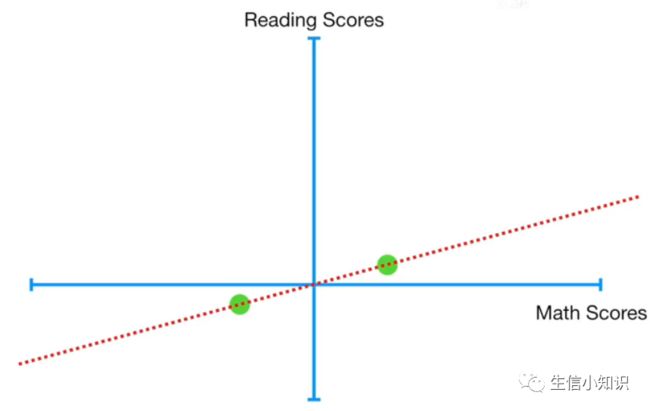
现在想象一下数学和阅读分数是 100% 相关的：

我们把数据中心化，然后我们找到了最适合的直线 (PC1)：

从技术上讲, 我们可以找到一条垂直于 PC1 的线为 PC2 ，但如果我们把数据投射到这条线上, 所有数据就会全部回到原点，这意味着新线的特征值为0，这意味着 PC1 解释了方差的 100%, PC2 解释 0%。

如果我们只有两个学生，然后我们将数据中心化, 然后找到最佳拟合线 (PC1)，然后就像之前, 我们可以找到一条垂直于 PC1 的线, 但是特征值是 0。所以, 和刚才一样, 只有一个主成分。(两点只能定义一条线)

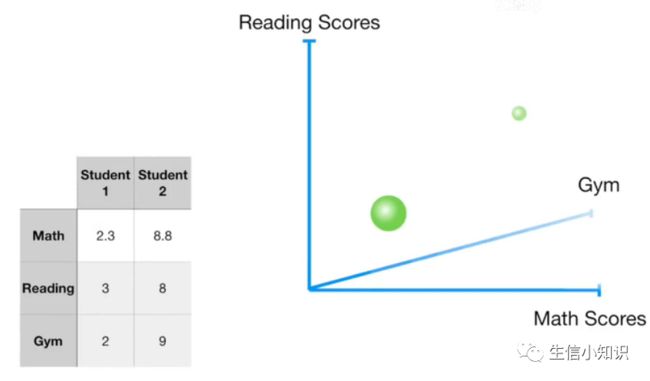
现在想象一下我们有两个学生, 分别有三个考试成绩: 数学, 阅读和体操(2个样本，3个变量)。我们可以把数据中心化, 同理, 因为我们只有两点, 两点定义一条线，我们只有 1 个主成分：

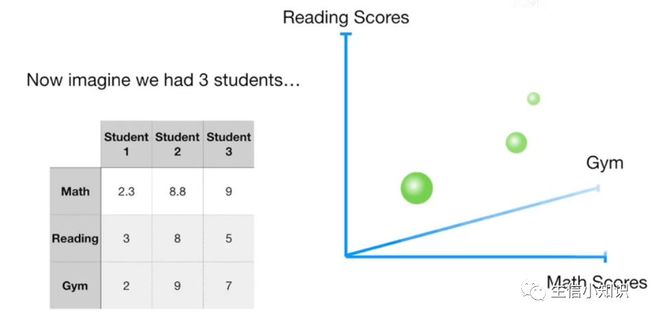
假设我们有 3 个学生， 3 个点定义一个平面, 一个平面只有 2 个轴，然后我们可以预测只有 2 个主成分：

总结一下：

从技术上讲, 数据集中的每个变量都有一个主成分，但是, 如果样本少于变量，然后样本数可以作为特征值大于 0 的 P C的个数的上限 (载荷值大于 0 的PCs 数量要小于等于样本数)