pca主成分分析结果解释_主成分分析(PCA)原理精讲

引言：当数据维度较高时，我们很难通过普通的方法做图，更不能分析样本间的关系。故我们接下来学习降维度、可视化的主成分分析(Principal Component Analysis，PCA)。

1.何时使用PCA

假设我们有如下的数据：有6小鼠的4个基因的表达数据，我们想要探索基于这4个基因的表达数据是否能区分小鼠间的差异。

gene	Mouse 1	Mouse 2	Mouse 3	Mouse 4	Mouse 5	Mouse 6
Gene 1	10	11	8	3	2	1
Gene 2	6	4	5	3	2.8	1
Gene 3	12	9	10	2.5	1.3	2
Gene 4	5	7	6	2	4	7

• 如果只考虑一个基因(gene 1)，将其绘制到一维坐标轴上。即使这只是一个简单的一维数据，它也可以展示出mouse4/5/6之间更为相似，mouse1/2/3之间更为相似。如下：

• 如果将2个基因(gene 1和gene 2)展示在2D-plot中。可以发现，mouse4/5/6之间更为相似，表现为gene 1和gene2表达较低；mouse1/2/3之间更为相似，表现为gene 1和gene 2表达较高。如下：

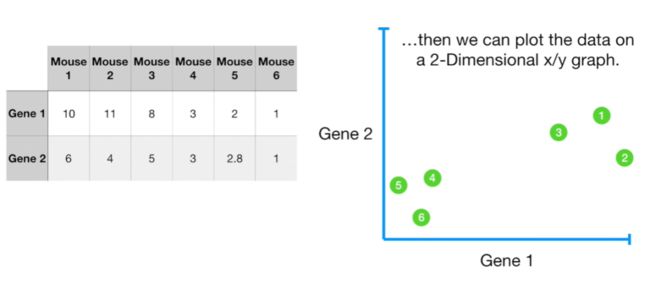
• 如果将3个gene(gene 1/gene 2/gene 3)展示在3D-plot中，gene 1为水平轴，gene 2 为纵轴，gene 3为垂直于gene 1和gene 2的轴(类似于z 轴，gene 3的表达量越低，离原点越近，体积越大，相反则体积越小)。可以发现靠近原点的3个mouse的基因表达量更为相似，表现为3个基因低表达；而远离原点的3个mouse的表达量更为相似。如下：

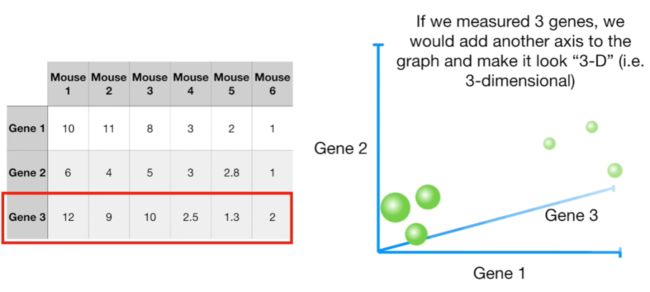
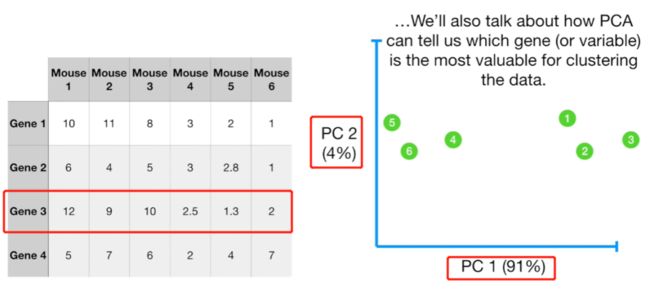
• 如果要把4个gene的数据全部绘制在图形中，我们将不能再用以上的方法直观展示小鼠中4个基因的表达量。但却可以使用PCA 2-D图来展示变量的分布情况，如下:横坐标对应主成分1(PC1)和纵坐标对应主成分2(PC2)。

在接下来的几个章节中:

• 讨论PCA如何处理4个及以上变量的数据并将其展示在2-D PCA图中。
• 讨论PCA是如何告诉我们哪一变量对数据聚类的影响最大。例如PCA可能告诉我们gene 3 对沿着x-轴(PC 1)分布数据的影响最大(为什么呢？从原始数据来说，gene 3的变异程度最大；从PCA图来说，gene 3在PC1中的组成比例最高，这将在后续的讨论中介绍)。

2. PCA计算原理

为了理解PCA是如何得到降维后的数据，我们从最简单的含有2个基因的数据集开始讨论。

gene	Mouse 1	Mouse 2	Mouse 3	Mouse 4	Mouse 5	Mouse 6
Gene 1	10	11	8	3	2	1
Gene 2	6	4	5	3	2.8	1

2.1 PCA第一步：寻找数据的质心(center of the data)

计算各小鼠gene 1表达量的平均值X_{gene 1}；计算各小鼠gene 2表达量的平均值X_{gene 2}；得到该数据集的质心(X_{gene 1}，X_{gene 2}).

2.2 PCA第二步：中心化。以质心(center)为中心，整体平移直至质心(center)与坐标轴原点(origin)重合。

注意：整体移动后，样本与样本之间的相对位置并不发生改变。

2.3 PCA第三步：做经过质心(origin)的一条随机直线对数据进行拟合，然后以质心为中心进行旋转，直至找对最佳拟合直线(PC1)。

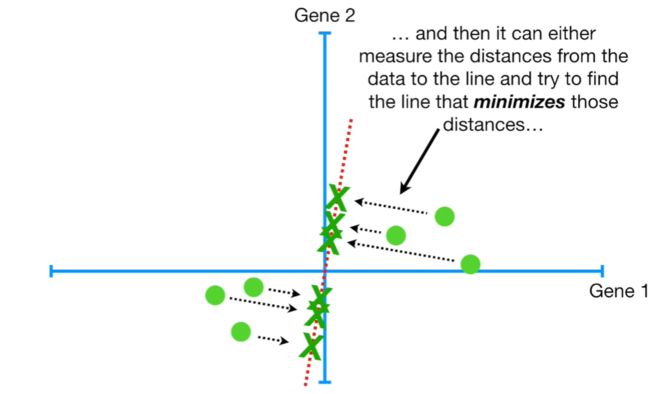
PCA如何定义最佳拟合直线？如下图，所有样本垂直投射至该条过质心的随机直线(红色虚线)，交点为投射点(projected point)。定义的方法有2种:

• 一种方法是：满足所有样本到该直线的距离之和最小。
• 另一种方法是：满足所有投射点到原点的距离之和最大。

---

注：这两种方法代表的意义相同，得到的结论也是一致的。

如下，随机选取一个样本，做该样本至随机直线的垂线(长度为b)，并将该样本与原点连接(长度为a)。试想一下，我们随机转动该随机直线(c所在的直线)，样本到原点的距离(a)将保持不变，而另外两条直角边(c和b)将发生变化。

• 如果我们利用直角三角形勾股定理来表示该直角三角形三条边的关系，便可以得到如下关系：
  • a²=b²+c²。
• 在a²保持不变的情况下，b²越小，则c²越大。
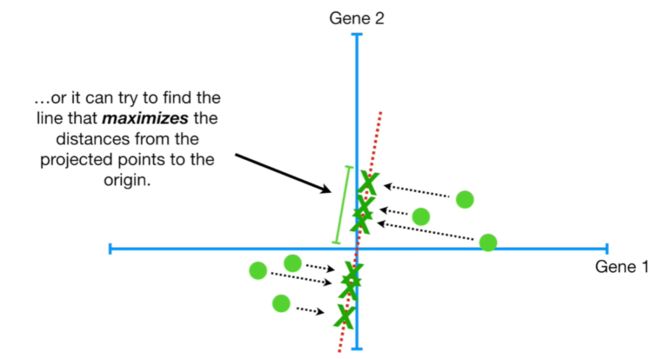
• 故在定义最佳拟合直线时，所有样本对应b²之和最小或者对应c²之和最大均可。但是在计算的时候，计算c更加容易，故PCA在寻找最佳拟合直线的时候，利用的是所以样本对应的c²之和最大。

---

在寻找最佳拟合直线时，样本1对应的c2为d1²，样本2对应的c2为d2²，样本3对应的c2为d3²，以此类推......

定义：d1² + d2² + d3² + d4² + d5² + d6² = sum of squared distances(距离平方和) = SS(distance)。

当SS(distance)取得最大值时，该直线为最佳拟合直线，称该条直线为主成分1(principal component 1，PC1)。

最佳拟合直线(PC1)解析。

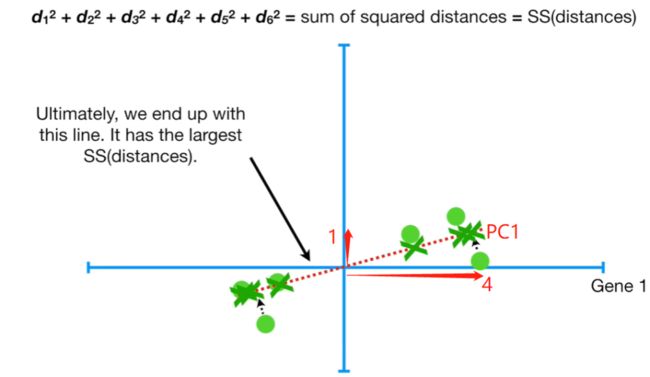
当SS取得最大时，便可得到最佳拟合直线。通过求解直线，我们可以知道PC1的斜率为0.25。也就是说，gene 1变化4个单位的同时，gene 2变化1个单位。数据沿Gene 1的变化幅度大于沿gene 2的变化幅度。

如果用鸡尾酒来形容PC1，那么PC1由4部分gene 1和1部分gene 2混合而成。鸡尾酒配方中的比率告诉我们，gene 1在描述数据的分布时更加重要。鸡尾酒配方的术语：PC1是gene 1和gene 2的线性组合。

最佳拟合直线(PC1)的SVD(奇异值分解)。

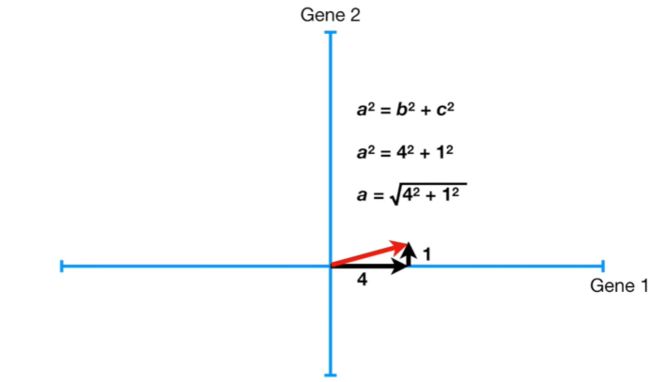根据勾股定理：在PC1上，当gene 1 = 4，gene 2 = 1，此时斜边 = 4.12。

当使用SVD进行PCA分析时，PC1需要将斜边进行归一化(scaled to 1)。故需要将直角三角形的三边同时进行归一化，将三条边同时除以4.12。将PC1归一化后，组成PC1的gene1和gene 2的配方发生改变，PC 1 由0.97部分gene1和0.242部分gene2组成。尽管配方的值发生可改变，但是gene 1与gene2组成的比值保持不变，依然为4。

术语小结

• 特征向量(奇异向量)：类似于高中阶段学的法向量。最佳拟合直线(PC 1)上，由0.97个单位gene 1 和0.242个单位gene 2正交组成的1 个单位长度向量，被叫做PC 1的奇异向量(singular vector)或者特征向量(Eigenvector)。其中每个gene的组成部分(如0.97个单位gene 1 和0.242个单位gene 2)，被称为因子载荷(loading scores)。
• 特征值：sum of squared distance = SS(distances)。PCA中，称最佳拟合直线的SS(distances)为PC1的特征值(Eigenvalue)。
• 奇异值：SS(distances for PC1) = Eigenvalue for PC1；SS(distances for PC1) 的平方根= singular value for PC1。PC1特征值的平方根称为PC1的奇异值。

2.4 PCA第四步：PC2

在2D-plot中，过原点做PC1的垂线，这样的垂线仅有一条，故该直线即为PC2。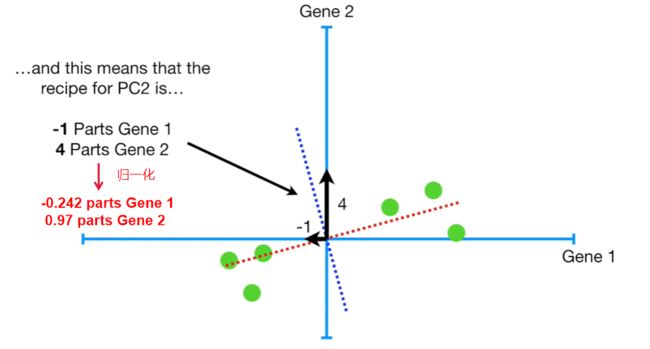

• PC2与PC1相互垂直，故可根据PC1的性质推导PC2的特征。
  • PC2的斜率为-4，有4部分的gene 2和-1部分的gene 1组成。
  • 特征向量：利用VSD进行PCA分析时，将PC2进行归一化后，PC2的单位向量由-0.242 部分gene 1和0.97部分gene 2组成，故PC2的奇异向量或特征向量为(-0.242,0.97)。
  • 因子载荷：-0.242和0.97分别为gene1和gene2的因子载荷(loading scores)，因子载荷告诉我们gene 2的重要性是gene 1的4倍。
  • PC2的特征值：同PC1一样，在PC2轴上，定义原点到样本投射点的距离为d。故PC2的特征值=d1²+d2²+d3²+d4²+d5²+d6²=sum of squared distances(距离平方和)=SS(distance)。

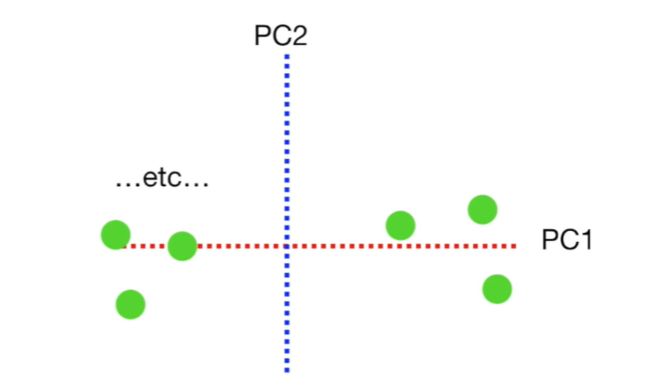
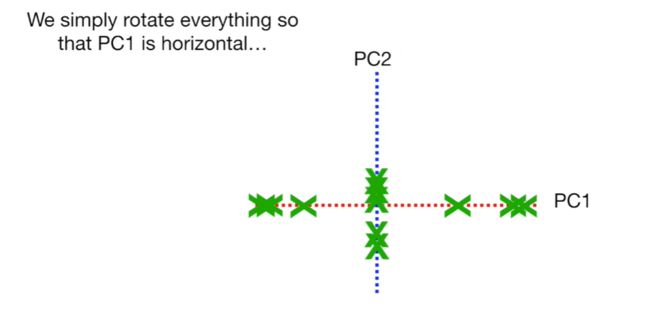
2.5 PCA第五步：绘制PCA plot

• 将样本分别投射至PC1和PC2轴上，同时旋转PC1轴和PC2轴，使得PC1轴为新的水平轴使得PC2轴为新的纵轴，即获得最终的PCA图。

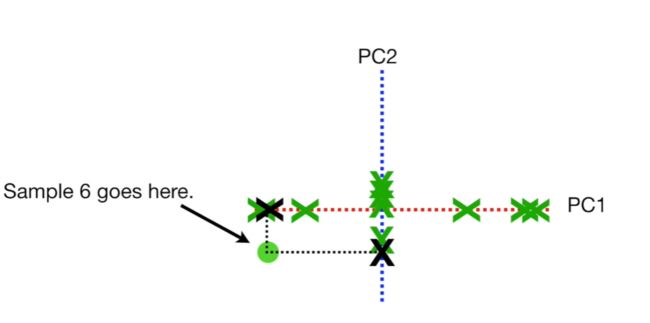
• 对于新的PCA-plot，同一样本来源的PC1和PC2的坐标轴又对应其来源样本。如下图中，同一样本投射至PC1和PC2后，其对应坐标的交点又还原为同一个样本的数据(如样本6)。

• 同理，利用PC1和PC2依次还原所有的样本。至此结束。以上便是SVD如何完成PCA分析的全部过程。

特征值除以(总样本数-1)计算样本围绕原点的变异。即

• SS(distances for PC1) / (n-1) = variation for PC1
• SS(distances for PC2) / (n-1) = variation for PC2

假设在以上分析的数据中，the variation for PC1=15, the variation for PC 2=3。那么总变异=15+3=18.

• PC1 变异所占总变异的百分比为：the variation for PC1/ total variation = 15/18=0.83,
• PC2变异所占总变异的百分比为：the variation for PC2/ total variation = 3/18=0.17

碎石图(scree plot)展示每个主成分(PC)所占的百分比。 故利用碎石图展示此分析分结果如下：PC1=83%，PC2=17%。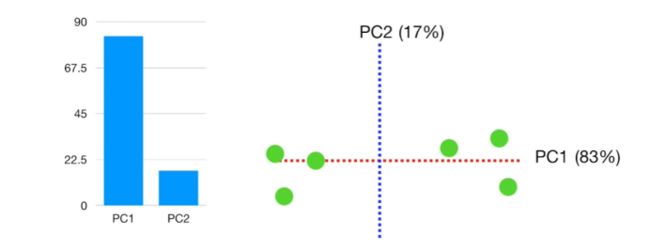

3.高维数据的PCA

3.1 三维数据

完成了2个变量数据中的PCA分析，我们继续在3个变量的数据中进行PCA分析。

3个变量中的PCA与2个变量的PCA方法一致。唯一不同的是，在寻找到PC1和PC2之后，需要继续寻找PC3。然后，根据所有主成分的特征值计算其对应的变异，并计算其所占总变异的百分比、绘制scree plot。在该数据中，PC1占总变异的79%；PC2占总变异的15%；PC3占总变异的6%。

因为PC1和PC2能解释94%的数据变异，故仅含PC1和PC2的2D-plot便可以很好的展示该3D数据的分布。最后，仅保留3-D PCA中的样本和PC1、PC2，将3D-图转化成2-D PCA图。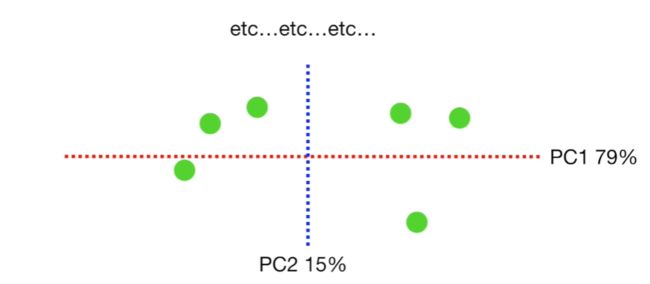

理论上来说，每一个变量中有一个主成分，但是实际上PC的数量等于变量或样本数量(数量较少的变量或样本)的个数(这将在后面的学习中详细讨论)。

3.2 四维数据

如果我们的样本中有4个变量(gene)，那么将不能在4-D graph中展示结果。即使展示出来，也会让人眼花缭乱。但是我们却可以使用PCA (不论我们是否做图均可)和绘制scree plot。

在4个变量中进行PCA分析的方法同前。最后，我们可以将数据投射到前2个主成分(PC1和PC2)，得到scree plot和2-D PCA Plot，如下：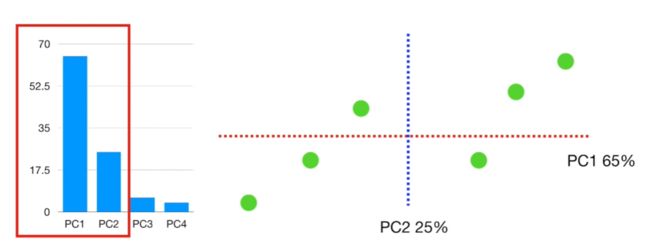

4.小结

本小节主要讲述了在何时使用PCA，探讨了实现PCA的主要原理。接着在下一小节，我们将讨论几个在PCA实践中的注意事项。

参考视频：https://www.youtube.com/watch?v=FgakZw6K1QQ&list=PLblh5JKOoLUICTaGLRoHQDuF_7q2GfuJF&index=24

编辑：吕琼

校审：罗鹏