ISLR读书笔记十九：主成分分析（PCA）

前面写的一些统计学习方法都是属于监督学习（supervised learning），这篇主成分分析（principal components analysis，简称 PCA ）和下一篇聚类分析（clustering）都是属于非监督学习（unsupervised learning）。

之前 ISLR读书笔记十二 中已经提到过主成分这一概念。其主要目的是利用一小部分数据组合，尽可能多地体现 全部数据的特征，从而实现降维的作用。

这里的 尽可能多地体现 可以有两种解读：

1. 将数据投影到方差最大的方向上，尽可能保留方差信息
   

2. 低维空间下的最佳近似。
   

从第一种解读出发，计算第一主成分：
令
$$Z_1={\varphi }_{11}{X}_1+{\varphi }_{21}{X}_2+\cdots +{\varphi }_{p1}{X}_p$$

这里要求 ${\sum }_{j=1}^p{\varphi }_{j1}^2=1$，${\varphi }_{11},{\varphi }_{21},\cdots ,{\varphi }_{p1}$ 称作加载（loadings），${\varphi }_1=({\varphi }_{11}{\varphi }_{21}\cdots {\varphi }_{p1})$ 称作加载向量（loading vector）
由于只关心数据的方差，所以可以对数据进行中心化，即要求$E(X_i)=0$
对于每一个分量
$$z_{i1}={\varphi }_{11}{x}_{i1}+{\varphi }_{21}{x}_{i2}+\cdots +{\varphi }_{p1}{x}_{ip}$$

第一主成分使得样本方差最大。即
$$\underset{{\varphi }_{11},\dots ,{\varphi }_{p1}}{\mathrm{maximize}}\left\{\frac{1}{n}\sum _{i=1}^n{\left(\sum _{j=1}^p{\varphi }_{j1}{x}_{ij}\right)}^2\right\}\text{ subject to }\sum _{j=1}^p{\varphi }_{j1}^2=1$$
由于 $\frac{1}{n}{\sum }_{i=1}^n{x}_{ij}=0$，所以即，使得 $\frac{1}{n}{\sum }_{i=1}^n{z}_{i1}^2$ 最大。这里，$z_{11},\cdots ,z_{n1}$ 称作分数（scores）

该优化问题，可以用奇异值分解（SVD）的方法解得。

第二主成分是所有与第一主成分 $Z_1$ 不相关（uncorrelated）的，关于 $X_1,\cdots ,X_p$ 的线性组合中，方差最大的线性组合。令
$$z_{i2}={\varphi }_{12}{x}_{i1}+{\varphi }_{22}{x}_{i2}+\cdots +{\varphi }_{p2}{x}_{ip}$$
可以证明 $Z_2$ 与 $Z_1$ 不相关，等价于加载向量 ${\varphi }_2$ 与 ${\varphi }_1$ 正交。

第三主成分是所有与 $Z_1$ 、$Z_2$ 不相关（uncorrelated）的，关于 $X_1,\cdots ,X_p$ 的线性组合中，方差最大的线性组合。以此类推。

从第二种解读出发，第一主成分加载向量是 $p$ 维空间中，最接近 $n$ 个观测数据的直线（在欧式距离平方的均值下最接近）。
更一般地，前 $M$ 个主成分的分数向量和加载向量，构成了原始 $p$ 维数据在 $M$ 维空间的最佳近似，即
$$x_{ij}\approx \sum _{m=1}^M{z}_{im}{\varphi }_{jm}$$

另外 PCA 还有其他一些需要注意的点：

规模化：
数据通常需要提前进行规模化（scaled）（每个变量乘以不同的常数），使得每个自变量的标准差为1。否则如果有部分变量方差特别大，那么PCA 的结果会受很大影响。

唯一性
每一个主成分在相差一个正负号的意义下式唯一的

被解释方差比例
我们通常关心前几个主成分反映了多少方差
数据总方差定义如下
$$\sum _{j=1}^p\text{Var}(X_j)=\sum _{j=1}^p\frac{1}{n}\sum _{i=1}^n{x}_{ij}^2$$
第 $m$ 个主成分的被解释方差定义如下：
$$\frac{1}{n}\sum _{i=1}^n{z}_{im}^2=\frac{1}{n}\sum _{i=1}^n{\left(\sum _{j=1}^p{\varphi }_{jm}{x}_{ij}\right)}^2$$
第 $m$ 个主成分被解释方差的比例（proportion of variance explained）
即为
$$\frac{{\sum }_{i=1}^n{\left({\sum }_{j=1}^p{\varphi }_{jm}{x}_{ij}\right)}^2}{{\sum }_{j=1}^p{\sum }_{i=1}^n{x}_{ij}^2}$$

决定主成分的个数
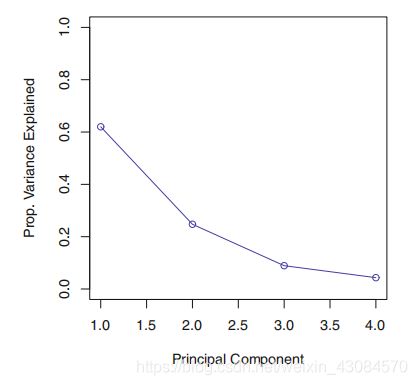
可以通过碎石图（scree plot），来决定主成分的个数
方法是寻找一个点，在这个点之后的点，主成分被解释方差比例很小