Python图像处理【9】使用高通滤波器执行边缘检测

0. 前言

高通滤波器 (High Pass Filters, HPF) 是一系列滤波器，这些滤波器仅允许来自图像频率响应(使用 DFT 获取)的高频部分通过，并过滤所有小于截止值的低频部分。使用逆 DFT 重建图像时，由于高频分量对应于边缘/细节等，因此利用 HPF 可以提取或增强图像中的边缘/细节。在本节中，我们将学习如何使用 OpenCV 的 FFT 模块实现 HPF 检测图像中对象边缘，例如 Ideal、Gaussian 和 Butterworth HPF。

1. 高通滤波器频率响应函数

下表中给出了几种常用高通滤波器 (High Pass Filters, HPF) 的频率响应函数 H：

Ideal HPF	Gaussian HPF	Butterworth HPF
$H(u,v)=\{\begin{array}{rcl}0& & D(u,v)\le D_0\\ 1& & D(u,v)>D_0\end{array}$	$H(u,v)=1-e^{-D^2(u,v)/2D_0^2}$	$H(u,v=\frac{1}{1+(\frac{D_0}{D(u,v)}{)}^{2n}}$

其中，$D(u,v)=\sqrt{u^2+v^2}$，$D_0$ 为截止频率，$n$ 为滤波器度。接下来，我们使用 OpenCV FFT/IFFT 函数实现以上的 HPF。

2. 利用 HPF 执行边缘检测

(1) 我们首先定义函数 dft2() 以实现 2D DFT，该函数执行以下操作：

• 将输入图像转换为浮点类型
• 使用 cv2.dft() 函数应用 DFT 获取输出
• 将原点从左上角转移到图像的中心
• 提取振幅和相位图像，并返回

import cv2
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import make_axes_locatable
from matplotlib.ticker import LinearLocator, FormatStrFormatter
from skimage.color import rgb2gray

def dft2(im):
    freq = cv2.dft(np.float32(im), flags = cv2.DFT_COMPLEX_OUTPUT)
    freq_shift = np.fft.fftshift(freq)
    mag, phase = freq_shift[:,:,0], freq_shift[:,:,1]
    return mag + 1j*phase

(2) 现在，定义函数 idft2() 以计算 2D-IDFT，该函数执行以下操作：

• 根据复杂功率谱输入中分离幅度和相位
• 将幅度提高到接近 1 的次方，大于 1 的值会增加对比度，小于 1 的值会降低对比度
• 将幅度和相位转换为笛卡尔实分量和虚分量
• 将笛卡尔分量组合成一个图像
• 将原点从图像中心移到左上角
• 使用 cv2.idft() 计算 IDFT 以获得输出
• 将输出组合到空间域图像中

函数 cv2.idft() 计算 1D 或 2D 数组的反离散傅立叶变换，调用方式如下所示：

cv2.idft(src, flags, nonzeroRows)

默认情况下，cv2.dft() 和 cv2.idft() 并不会缩放结果。因此，我们需要将 DFT_SCALE 显式传递给 cv2.dft() 或 cv2.idft()，以使这些变换互逆：

def idft2(freq):
    real, imag = freq.real, freq.imag
    back = cv2.merge([real, imag])
    back_ishift = np.fft.ifftshift(back)
    im = cv2.idft(back_ishift, flags=cv2.DFT_SCALE)
    im = cv2.magnitude(im[:,:,0], im[:,:,1])
    return im

(3) 接下来，我们使用前言中介绍的公式实现 HPF，对于给定的截止频率 $D_0$，每个函数都接受核大小参数 sz：

def ideal(sz, D0):
    h, w = sz
    u, v = np.meshgrid(range(-w//2,w//2), range(-h//2,h//2)) #, sparse=True)
    return np.sqrt(u**2 + v**2) > D0

def gaussian(sz, D0):
    h, w = sz
    u, v = np.meshgrid(range(-w//2,w//2), range(-h//2,h//2)) #, sparse=True)
    return 1-np.exp(-(u**2 + v**2)/(2*D0**2))

def butterworth(sz, D0, n=1):
    h, w = sz
    u, v = np.meshgrid(range(-w//2,w//2), range(-h//2,h//2)) #, sparse=True)
    return 1 / (1 + (D0/(0.01+np.sqrt(u**2 + v**2)))**(2*n))

(4) 实现函数 plot_HPF()，该函数接受输入图像、HPF 函数和截止频率列表，以绘制通过在输入图像上应用 HPF 获得的输入/输出图像、以及不同截止值的 HPF 功率谱：

def plot_HPF(im, f, D0s):
    freq = dft2(im)
    fig = plt.figure(figsize=(20,20))
    plt.subplots_adjust(0,0,1,0.95,0.05,0.05)
    i = 1
    for D0 in D0s:
        freq_kernel = f(im.shape, D0)
        convolved = freq*freq_kernel # by the Convolution theorem
        im_convolved = idft2(convolved).real
        im_convolved = (255 * im_convolved / np.max(im_convolved)).astype(np.uint8)
        plt.subplot(2,2,i)
        last_axes = plt.gca()
        img = plt.imshow((20*np.log10(0.01 + freq_kernel)).astype(int), cmap='coolwarm')
        divider = make_axes_locatable(img.axes)
        cax = divider.append_axes("right", size="5%", pad=0.05)
        fig.colorbar(img, cax=cax)
        plt.sca(last_axes), plt.title('{} HPF Kernel (freq)'.format(f.__name__), size=10)
        plt.subplot(2,2,i+2), plt.imshow(im_convolved), plt.axis('off')
        plt.title(r'output with {} HPF ($D_0$={})'.format(f.__name__, D0), size=10)
        i += 1
    plt.show()

(5) 实现函数 plot_HPF_3d() 以绘制对应于输出图像的 3D 频率响应，输出图像通过在输入图像上应用由一组截止频率参数化的给定 HPF 函数获得：

def plot_HPF_3d(im, f, D0s):
    freq = dft2(im)
    fig = plt.figure(figsize=(20,10))
    plt.subplots_adjust(0,0,1,0.95,0.05,0.05)
    i = 1
    for D0 in D0s:
        freq_kernel = f(im.shape, D0)
        convolved = freq*freq_kernel # by the Convolution theorem
        Y = np.arange(freq_kernel.shape[0])
        X = np.arange(freq_kernel.shape[1])
        X, Y = np.meshgrid(X, Y)
        Z = (20*np.log10( 0.01 + convolved)).real
        ax = fig.add_subplot(1, 2, i, projection='3d')
        surf = ax.plot_surface(X, Y, Z, cmap=plt.cm.coolwarm, linewidth=0, antialiased=False)
        ax.zaxis.set_major_locator(LinearLocator(10)), ax.zaxis.set_major_formatter(FormatStrFormatter('%.02f'))
        ax.set_xlabel('F1', size=15), ax.set_ylabel('F2', size=15)
        plt.title(r'output with {} HPF (freq)'.format(f.__name__, D0), size=10)
        fig.colorbar(surf, shrink=0.5, aspect=10)
        i += 1
    plt.show()      

(6) 给定核大小和截止频率，实现函数 plot_filter_3d() 绘制 HPF 核的 3D 功率谱：

def plot_filter_3d(sz, f, D0s, cmap=plt.cm.coolwarm):
    fig = plt.figure(figsize=(20,10))
    plt.subplots_adjust(0,0,1,0.95,0.05,0.05)
    i = 1
    for D0 in D0s:
        freq_kernel = f(sz, D0)
        Y = np.arange(freq_kernel.shape[0])
        X = np.arange(freq_kernel.shape[1])
        X, Y = np.meshgrid(X, Y)
        Z = (20*np.log10( 0.01 + freq_kernel)).real
        ax = fig.add_subplot(1, 2, i, projection='3d')
        surf = ax.plot_surface(X, Y, Z, cmap=cmap, linewidth=0, antialiased=False)
        ax.zaxis.set_major_locator(LinearLocator(10))
        ax.zaxis.set_major_formatter(FormatStrFormatter('%.02f'))
        ax.set_xlabel('F1', size=15)
        ax.set_ylabel('F2', size=15)
        ax.set_title('{} HPF Kernel (freq)'.format(f.__name__), size=10)
        fig.colorbar(surf, shrink=0.5, aspect=10)
        i += 1

(7) 绘制原始输入图像：

im = plt.imread('1.png')
im = rgb2gray(im)
plt.figure(figsize=(7,12))
plt.imshow(im, cmap='gray'), plt.axis('off'), plt.title('original image')
plt.show()

(8) 我们使用不同的截止频率值的 HPF，绘制 Ideal HPF 和输入/输出图像的频率响应：

D0 = [10, 30]

plot_HPF(im, ideal, D0)

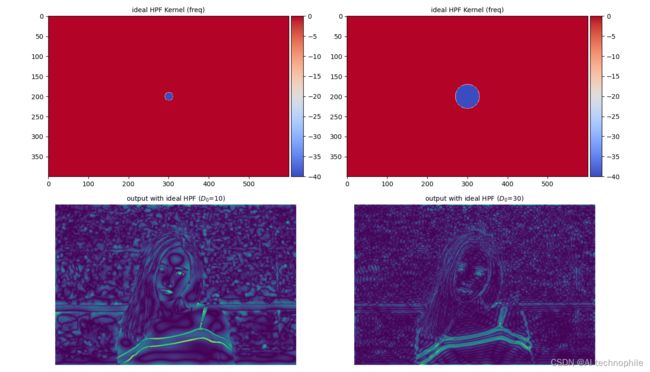
从上图中可以看出，Ideal HPF 减弱了图像中的低频部分，由于函数值的 0-1 突变导致了图像中出现了之振铃伪影。

(9) 接下来，我们使用函数 plot_hpf_3d() 绘制输出图像的频率响应：

plot_filter_3d(im.shape, ideal, D0)

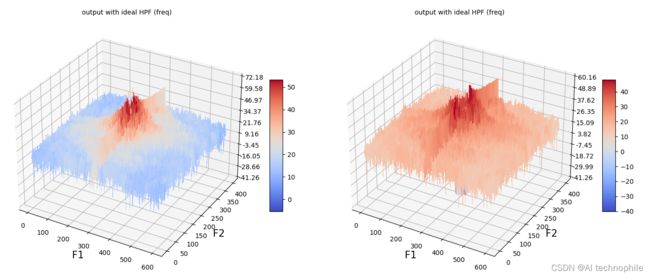
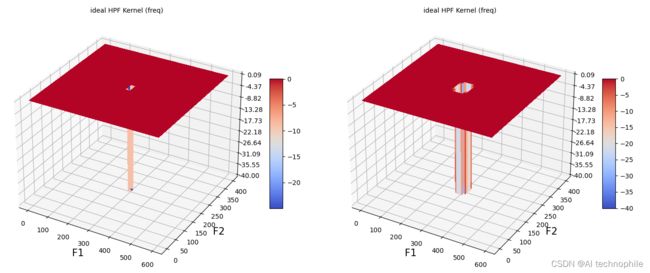
(10) 使用函数 plot_filter_3d() 绘制不同截止值的 Ideal HPF 核的功率谱：

plot_filter_3d(im.shape, ideal, D0)

(11) 接下来，使用 plot_hpf() 函数绘制 Gaussian HPF 和输入/输出图像的频率响应：

plot_HPF(im, gaussian, D0)

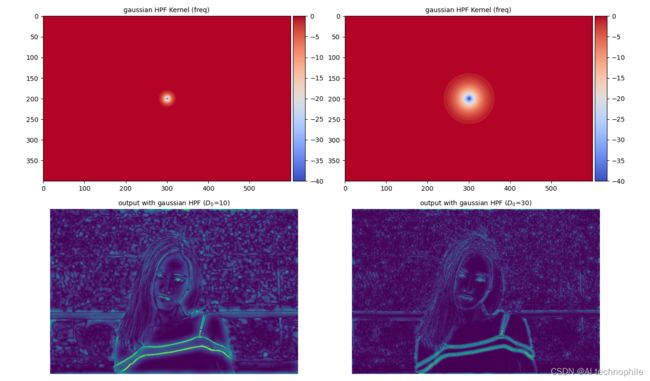
从上图可以看出，高斯 HPF 过滤了图像中的低频分量；同时，它消除了使用 Ideal HPF 导致的振铃伪影。

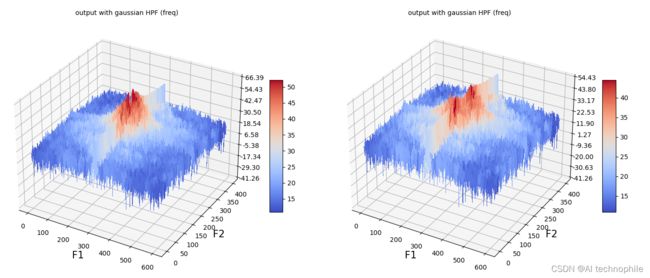
(12) 接下来，使用函数 plot_hpf_3d() 绘制输出图像的频率响应：

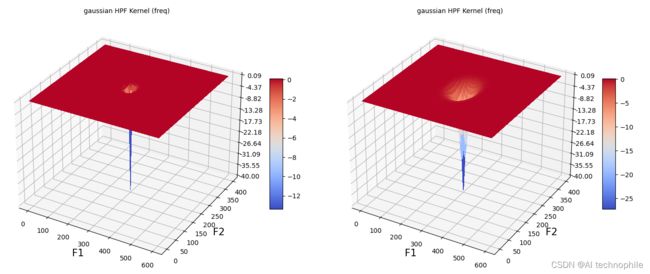
plot_HPF_3d(im, gaussian, D0)

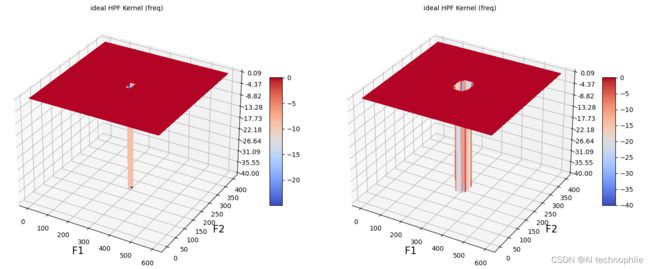
(13) 使用函数 plot_filter_3d() 绘制不同截止值的 Gaussian HPF 核的功率谱：

plot_filter_3d(im.shape, gaussian, D0)

(14) 接下来，用 plot_hpf() 函数绘制 Butterworth HPF 和输入/输出图像的频率响应：

plot_HPF(im, butterworth, D0)

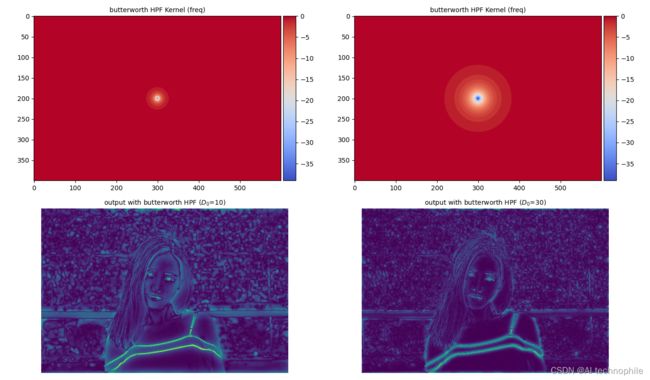
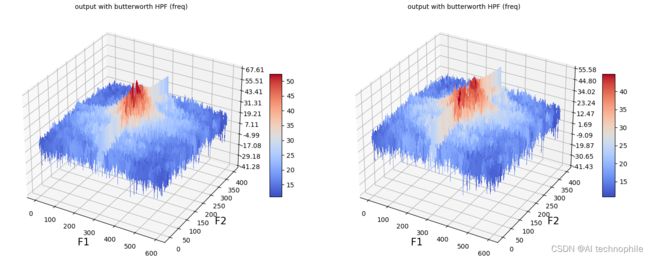
(15) 使用函数 plot_hpf_3d() 绘制输出图像的频率响应：

plot_HPF_3d(im, butterworth, D0)

(16) 使用函数 plot_filter_3d() 绘制不同截止值的 Butterworth HPF 核的功率谱：

plot_filter_3d(im.shape, butterworth, D0)

小结

高通滤波器可以允许高于给定阈值的频率信息通过，而过滤掉低于该阈值的频率信息，从而大大衰减低频率的一种滤波器。在图像处理中，过滤频率信息采用的是傅里叶变换，把图像从空域转为频域进行处理。在本节中，我们学习了如何使用高通滤波器执行边缘检测，使用 OpenCV 的 FFT 模块实现 HPF 检测图像中对象边缘。

系列链接

Python图像处理【1】图像与视频处理基础
Python图像处理【2】探索Python图像处理库
Python图像处理【3】Python图像处理库应用
Python图像处理【4】图像线性变换
Python图像处理【5】图像扭曲/逆扭曲
Python图像处理【6】通过哈希查找重复和类似的图像
Python图像处理【7】采样、卷积与离散傅里叶变换
Python图像处理【8】使用低通滤波器模糊图像