机器学习之kMeans聚类：日撸Java三百行day56-57

一、什么是kMeans聚类

在了解kMeans聚类之前，我们首先要理解聚类(cluster)与分类(classify)的区别。聚类与分类的英文名不同，也能够体现出它们的区别。但它们的中文名中都有一个“类”字，说明都是将一大堆实例分为几个类。而在如何分、怎么分、分成几坨等问题上，聚类与分类又有本质的区别。

•分类(classify)

分类是有监督学习方法中的一种，是从特定的数据中挖掘模式并作出判断的过程。必须先明确了解每个类别的信息，即：有标签。通过事先打好的标签来判断正误并学习，利用训练好的模型来分类测试数据集。如：垃圾邮件分类

•聚类(cluster)

聚类是无监督学习方法的一种，目的也是将数据分类，但事先不知道如何去分，即：无标签。聚类不知道目标变量是什么，也不知道最终的类别是什么。聚类算法是通过预先设置好的算法，通过自身判断实例之间的相似性进行聚类。相似度高的实例分为一簇。一般用于数据处理阶段。

了解了以上两个概念后，就能够区分分类与聚类了。常见分类算法如：KNN，都是使用提供一些带有标签的数据集。而本文介绍的聚类算法：kMeans，则是使用不提供标签的数据集。

•kMeans聚类算法

kMeans是聚类算法中最常用的一种，算法最大特点为简单易学，易于理解，且运算速度快。基本思想为：物以类聚，人以群分。k值代表着最终数据集通过聚类得到k个簇。算法通过衡量两个实例之间的距离，来判断两者是否分为一个簇。

二、kMeans聚类算法基本思想

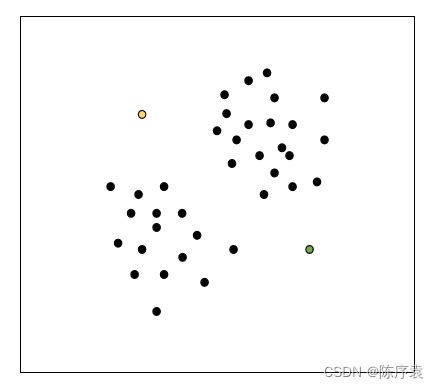
为了更好的理解kMeans聚类算法的基本思想，我们就以图为例，更加直观的介绍该算法。假设k=2，初始实例在二维空间分布状态如图所示：

1、由于k=2，因此最终需要分为两簇。每个簇都有一个质心(Centroid)，用于统领以及代表一整个簇。我们随机选择两个实例点作为质心，用黄色与绿色区分：

2、找到两位初始大哥（质心）后，就开始第一轮分簇。通过计算实例之间的距离，来代表实例之间的相似度。还是那句话：“物以类聚，人以群分”。距离越近，相似度越高，划分到同一个簇的可能性越高。

 

3、为了让大哥（质心）更加具有代表性，每个小团体需要另找一个实例作为大哥，用来更好的代表它们所在的簇。因此，需要计算当前簇内实例的距离均值。这个距离均值可能在数据集中不存在，因此可以将它假定为簇中的一个实例，并将它当作大哥：

4、找到新的大哥后，大哥认为它所带领的簇内有一些小弟（实例）离它太远了，不够忠诚。因此大哥们想要重新计算它周围的小弟与它之间的距离。若太远，则逐出它所带领的簇。：

 5、得到了新的簇以后，按照第3步，依然需要找到新的大哥（质心）来代表一个簇：

 6、得到了新的大哥（质心）以后，按照第4步，依然需要通过计算小弟（实例）到大哥的距离来重新分簇。若分后的簇与分前的簇一致，那么算法结束；否则，继续第5步。

 

三、算法的基本流程及操作

在介绍算法流程之前，先分析数据集。本次实验使用了iris数据集，数据量为150。为了保证无监督学习，我们只使用前四个属性：sepallength、sepalwidth、petallength、petalwidth。如：[5.1,3.5,1.4,0.2]表示该实例sepallength=5.1，sepalwidth=3.5，petallength=1.4，petalwidth=0.2。

sepallength	sepalwidth	petallength	petalwidth
5.1	3.5	1.4	0.2
4.9	3.0	1.4	0.2
...	...	...	...
5.9	3.0	5.1	1.8

以iris数据集处理为例，阐述kMeans算法的基本流程。代码都有注释。

①初始化全局变量，并读取数据文件。设置k值，即：要分成几个簇。

	public static final int MANHATTAN=0;//曼哈顿距离
	public static final int EUCLIDEAN=1;//欧几里得距离
	public int distanceMeasure=EUCLIDEAN;//默认距离测量策略为欧式距离
	public static final Random random=new Random();//获取随机数，随机选取k个质心
	Instances dataset;//数据集
	int numClusters=3;//分成三簇
	int[][] cluster;//簇矩阵，用于存储每个簇中的实例
	public KMeans(String paraFilename) {
		dataset=null;
		try {
			FileReader fileReader=new FileReader(paraFilename);//读取数据
			dataset=new Instances(fileReader);//将数据作为数据集
			fileReader.close();//关闭文件
		}catch (Exception ee) {
			System.out.println("Cannot read the file: " + paraFilename + "\r\n" +ee) ;
			System.exit(0);
			// TODO: handle exception
		}
	}
	public void setNumClusters(int paraNumClusters) {//设置簇数
		numClusters=paraNumClusters;
	}

为了更好地理解，需要对cluster矩阵作特别说明。[0,1,2,3,4,5,6,7,8]来代表实例，那么[[3, 6, 8],[0, 1, 2, 4],[5, 7]]代表着实例[3,6,8]被分到第0簇，实例[0,1,2,4]被分到第1簇，实例[5,7]被分到第2簇。

那么，我们可以将[0,1,2,3,4,5,6,7,8]转换为[1,1,1,0,1,2,0,2,0]。

②将数据集打乱。打乱后便于随机找k个大哥（质心）。

	public static int[] getRandomIndices(int paraLength) {
		int[] resultIndices=new int[paraLength];
		//第一步 初始化
		for(int i=0;i

③计算实例间的距离，用于分簇。常用距离度量方式有：欧氏距离、曼哈顿距离。本实验默认使用欧氏距离。

	public double distance(int paraI,double[] paraArray) {//计算某点与簇间距离
		int resultDistance=0;
		double tempDifference;
		switch (distanceMeasure) {//选择某种度量方式
		case MANHATTAN://曼哈顿距离
			for(int i=0;i

④聚类算法，主要分为三步：随机找k个大哥——划分簇——重新找大哥。算法终止条件为：划分后的簇与划分前的簇相同。

	public void clustering() {//聚类算法
		int[] tempOldClusterArray=new int[dataset.numInstances()];//原来的簇数组,numInstance为求出数据数据，此处为150
		tempOldClusterArray[0]=-1;
		int[] tempClusterArray=new int[dataset.numInstances()];//150
		Arrays.fill(tempClusterArray, 0);//用0填充数组
		double[][] tempCenters=new double[numClusters][dataset.numAttributes()-1];//用于记录簇中心数据
		//第一步 初始化簇中心，此处是随机找k个
		int[] tempRandomOrders=getRandomIndices(dataset.numInstances());
		for(int i=0;itempDistance) {
			    		tempNearestCenter=j;
			    		tempNearestDistance=tempDistance;
			    	}//of if
			    tempClusterArray[i]=tempNearestCenter;//记录第i个实例的中心
			    }//of for j
			}//of for i
			//2.2 找到新的中心
			tempClusterLengths=new int[numClusters];//新的类
			Arrays.fill(tempClusterLengths, 0);
			double[][] tempNewCenters=new double[numClusters][dataset.numAttributes()-1];//新的中心矩阵
			for(int i=0;i

⑤浅测一下。

	public static void testClustering() {
		KMeans tempKMeans=new KMeans("D:/software/eclipse/eclipse-workspace/day51/iris.arff");//读取数据
		tempKMeans.setNumClusters(3);//分为3簇
		tempKMeans.clustering();//进行聚类
	}
	public static void main(String args[]) {
		testClustering();
	}

四、一些问题

1、KNN算法与kMeans算法的区别？

KNN算法是分类算法，分类算法需要学习资料，即：标签。通过学习资料进行学习形成模型，再用于测试数据集。通过测试结果与测试数据集中的标签进行匹配，来判断算法的正确率。而kMeans是聚类算法，没有学习资料，也没有正确答案。同时，kMeans算法的训练过程需要反复迭代，KNN算法不需要迭代处理。kMeans算法中k代表着簇的个数，也代表质心的个数。KNN算法中的K代表与某实例最近的K个实例。

2、kMeans算法中k的取值？

在kMeans算法中，k的取值十分重要。使用该算法，需要事先制定要分成的簇树k，但由于先验知识缺乏，确定k值是十分困难的。通过查阅资料，了解到了一些常用的几种k值的选取方法：

1、简单粗暴法：k≈sqrt(N/2)，其中N为实例样本数量。

2、肘部法：顾名思义，就是找到一个“肘部”，即拐点。该方法需要绘制聚类结果随着聚类个数k变化的曲线，并找到曲线的拐点。将该拐点代表的k值作为最终k值。

如图所示，对于该数据集的聚类而言，最佳聚类数k=4。

3、 轮廓系数法：这是一种十分常见的聚类效果评价指标。该指标结合了内聚合度和分离度两个因素。通过计算聚类结果的轮廓系数来评判本次聚类效果。，S越接近于1，聚类效果越好。是通过计算所有样本点的轮廓系数的平均值得到。样本点的轮廓系数为：

其中，表示样本点到与其他属于同一簇的其他样本点的距离的平均值。越小，说明该样本属于该簇的可能性越大。表示样本点到其他簇中所有样本的距离的平均值。