CT图像重建简要介绍
0 说明
本文是个人学习CT重建的简要笔记。主要是医学图像重建的简单入门知识。
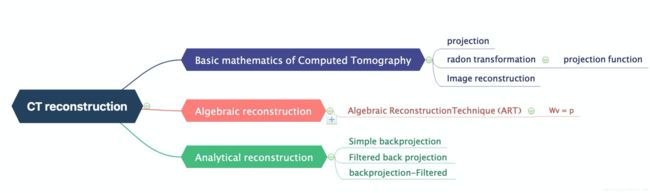
1 CT重建
CT图像是以不同的灰度来表示,反映器官和组织对X线的吸收程度。黑影表示低吸收区,即低密度区,如含气体多的肺部;白影表示高吸收区,即高密度区,如骨骼。但是CT 和X线图像相比,CT的密度分辨力高,即有高的密度分辨力(density resolution)。因此,人体软组织的密度差别虽小。吸收系数虽多接近于水,也能形成对比而成像。解剖成像。
Computer Tomography basically involves two distinct phases, the measurements of the projection data and the reconstruction of that data. each projection is a one-dimensional vector, and if you put all of the projection next to each other you can see all the projection data in one single image, this is called the Sinogram. so Computer Tomography handles data from two different domains. On one side is the volume domain which houses the scanned object and the reconstruction of volumes this is the spatial domain typically with a cartesian coordinate system. On the other side the projection domain houses as its name implies projection data, its data is typically defined on a coordinate system with projection direction on one axis and detector position on the others. The transition from the volume domain into the projection domain is called a forward projection, and form the projection domain to the volume domain is called back projection.
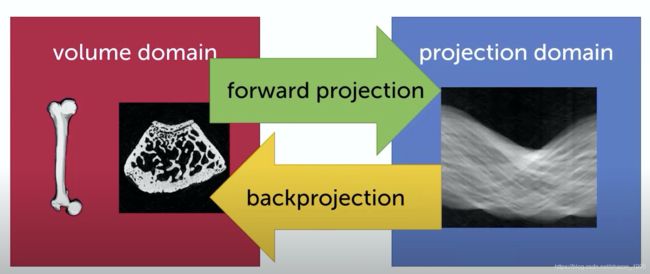
这部分的物理原理,将会在随后的文章里介绍。
2 Radon 变换
在理解重建之前,我们必须先知道正向投影的概念,这个过程就是我们获得投影数据的过程,即是我们在detector上收集到的数据。断层成像的基本原理就是设想有一个探测器绕着坐标轴的原点旋转,从不同的投影角度得到投影数据,这个过程也可以理解为线积分即是我们这里要说的Radon 变换。我们可以通过Radon 变换来模拟得到投影数据的过程。当然这里得到的数据只是模拟数据,与真实的CT的detector的数据差别还是很大的,真实情况中会有吸收和散射的问题。 若 f(x,y) 表示一个未知的密度,对 f(x,y) 做拉东变换,相当于得到 f(x,y) 投影后的信号。举例来说,f(x,y) 相当于人体组织,断层扫描的输出信号相当于对 f(x,y) 做拉东变换。 可以用拉东反变换从投影后的结果重建原始的密度函数 f(x,y)。Radon 变换的数学表达式:
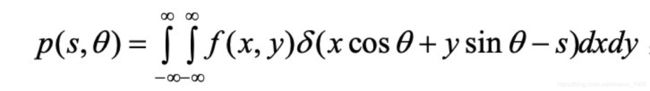
可以结合下图理解:

-
The inverse of the Radon transform can be used to reconstruct the original image from the projection data
-
The Radon transform data is often called a sinogram because the Radon transform of a Dirac delta function is a distribution supported on the graph of a sine wave
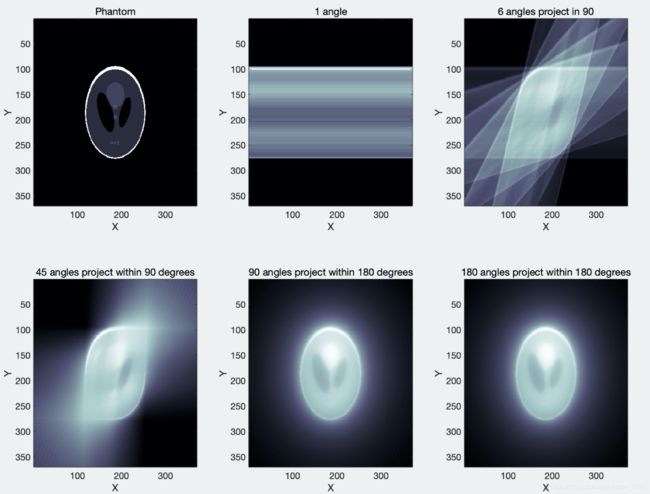
下图为radon逆变换重建出来的图像效果,这个重建速度还是比较快的:
Now I will introduce how to get projection data through radon transformation as the Simulated input data of reconstruction algorithm. radon transformation which is the approach affording projection is defined as a series of line integrals over the function in the spatial domain. Let f(x, y) be the density function defined on the x-y plane, and its projection function (i.e. ray sum, line integral, And Radon transformation) p(s, θ) has the following different equivalent expressions. Look at the figures at this page, The first picture is a head phantom image generated by the phantom function, the second picture is a sinogram obtained by radon transformation, and the third picture is an image reconstructed by radon inverse transformation.
3 重建方法分类
重建方法分为两类,直接法和间接法。
直接法即代数重建包括直接矩阵法和迭代重建技术以及很多改进的代数重建技术。
这里只简单的说明代数重建算法,具体实现的过程将会在随后的文章介绍。
分析重建中比较著名的算法是滤波反投影算法,这片文章的重点也是介绍这类算法,文章最后会附上相关的matlab实现code。
3.1 ART
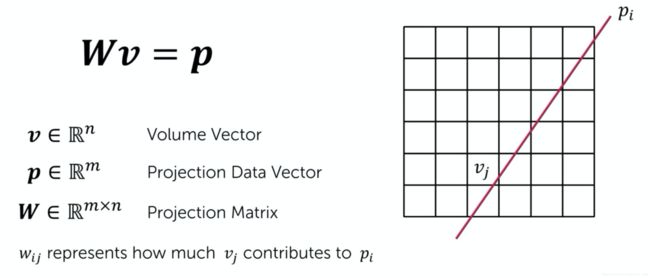
代数重建原理上就是解线性方程,这需要有比较好的线性代数的基础。我们都知道如果是方阵的话,线性方程组是有唯一解的。但是如果projection matrix是一个超定矩阵或者欠定矩阵,是没有数学上的精确的解的,这就引入了投影矩阵的概念。
algebraic reconstruction technique is all about a system of equations which isw times v equals p. in this formula v is one-dimensional vector of n elements, each representing the pixels of a certain 2d object, p is one-dimensional vector of m elements, each representing a measurements taken at a certain detector in a certain projection direction, w is called the projection matrix and each value in this matrix called a projection rate defines the contribution of a specific pixel to a specific detector.
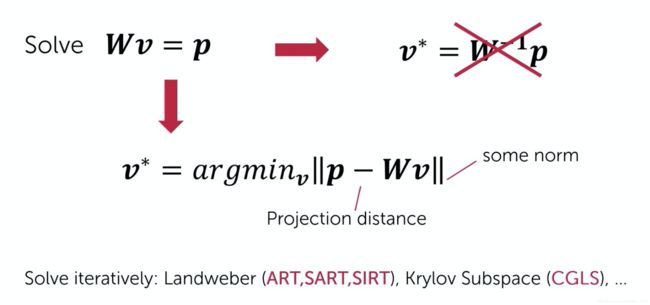
结果上图中least square的问题,有很多方法,比较常用的主要是梯度下降算法,正规方程法等。
3.2 FBP
介绍filtered back projection算法之前,先引入中心切片定理和反投影的简单原理。
-
反投影原理
用一个简单的图来说明一下反投影原理。反投影并不是能够把图像的各个像素值还原成与原图像一样,而是把各个角度的投影简单加和。 这就导致了会把原本像素值为零的地方,反投影后会有像素值,这也是我们常说的伪影。

知道了反投影的原理,大家不难发现,中间的部分明显是高频区,在加和的过程中强度很大,边缘地方是低频区,能量较低。给大家看一下直接反投影的一个效果。
然后再看一下再傅立叶域的一个效果,重点的亮的区域占有了90%以上的能量,这也是我们为什么要滤波,后面我们会讲最常用的一个斜坡滤波器。
-
中心切片定理
The Fourier transform of a parallel p
rojection of an object f(x,y) obtained at an angle θ equals a line in a two dimensional Fourier transform of f(x,y) taken at the same angle.
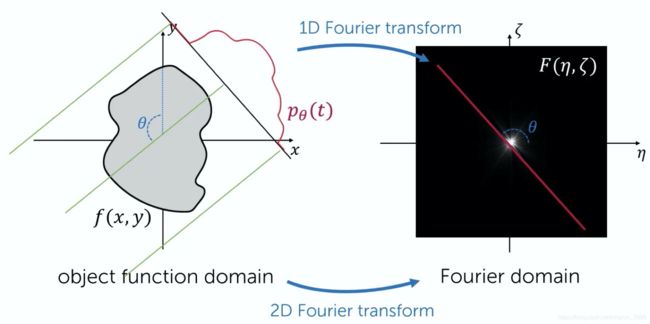
Analytical reconstruction methods are based on the fully a slice theory so in this blog I’ll explain exactly the concept behind this theorem and how in theory it can be used to build the reconstruction from a projection data . Anyway we have a two dimensional object function f represented on a cartesian domain. now to represent this function on the Fourier domain, you can simply apply a two dimensional Fourier transform on it. but of course in tomography we don’t know the object function, what we do know however are its detector functions for a set of different angles.
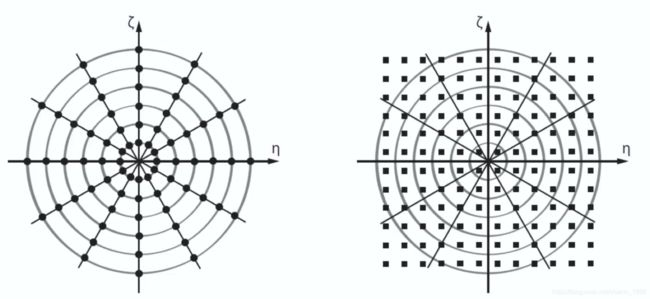
Sadly there are one or two problems with this approach all coming back to the fact that the amount of measurements in practice is finite which leads to a Fourier domain that is sampled in a difficult to work with way . one thing you’ll note immediately is that free samples lie in circles rather than on a square grid which is required for practical algorithms that perform the inverse transformation such as the fast Fourier transform. this means that we’ll have to apply interpolation in the Fourier domain which is not necessarily something that we like to do also not that the sampling distribution of the Fourier domain is much denser near the origin than it is for the outer regions. this means that for the lowest frequencies there is lots of data available, meaning that these low frequencies will be reconstructed fairly accurately. the high frequencies however which is where most of the finer details of the object are located, are not greatly sampled and will not be accurately reconstructed after the inverse Fourier transform. and this will lead to very blurry images. now does this mean that the freudian slice theorem is useless in practice? not really, because even though you can’t use it to directly create reconstructions, it does form the basics for another reconstruction methods called filtered backprojection. and filtered backprojection cleverly manages to overcome the problems of the fully alive stream by introducing an additional filtering phase and by replacing the inverse Fourier transform with a different operation but more on a future vedio.
- 滤波器
斜坡滤波器

Multiply the one-dimensional Fourier transform P(ω,θ) of the projection data p(s,θ) by |ω|. After that, do one-dimensional inverse Fourier transform on the product |ω| P(ω,θ). Finally, The reconstructed image is obtained by back-projecting the filtered projection data.

滤波后的图像展示:
可以在傅立叶域看下滤波后的傅立叶图像:
结束,这篇文章暂时就介绍到这里。
4 写在后面的话
代码如果解析还在这篇文章的话,就太长了,担心大家没有耐心看,所以准备再写一篇文章给大家说下代码实现另外在介绍一种先反投影后滤波的算法。
反投影和滤波的顺序是可以灵活的随意交换的,基于最基本的滤波反投影算法可以试着做一些更好的改进。本人研究生萌新,方向医学图像重建,欢迎有学习图像处理的集美们一起交流。